Квадратні рівняння

1. Квадратні рівняння.

2.

Завдання, які розв'язувалися за допомогою квадратних
рівнянь, зустрічаються в трактаті з астрономії
«Аріабхаттіам», написаним індійським астрономом і
математиком Аріабхатою І в 499 році нашої ери.
Аріабхата (вчення
Аріабхати) (499), в якому у
віршованій формі викладені
математичні відомості,
необхідні для
астрономічних обчислень;
приведені завдання на
складання і
розв'язування рівнянь,
знаходження квадратного і
кубічного коренів та інш.
Аріабхата (476–550), також
Аріабата,
індійський астроном і матема
тик.

3.

Один з перших відомих висновків формули коренів
квадратного рівняння належить індійському
вченому Брамагупті (близько 598 г.); Брамагупта
виклав універсальне правило розв'язування квадратного
рівняння,
Брамагу́пта—
давньоіндійський математик і ас
троном, який написав важливі
роботи
з математики та астрономії.

4.

У стародавній Греції квадратні рівняння розв'язувалися
за допомогою геометричних побудов. Методи, які не
пов'язувалися з геометрією, вперше наводить Діофант
Александрійський у III ст. У своїх книгах
«Арифметика» він наводить приклади розв'язування
неповних квадратних рівнянь.

5.

Загальне правило розв'язування квадратних рівнянь було сформоване
німецьким математиком М. Штифелем (1487 — 1567). Виведенням
формули загального розв'язку квадратних рівнянь займався Франсуа
Вієт. Він же й вивів формули залежності коренів рівняння від
коефіцієнтів у 1591 році. Після праць нідерландського математика А.
Жирара (1595 — 1632), а також Декарта і Ньютона спосіб
розв'язування квадратних рівнянь набув сучасного вигляду.
М. Штифель
Франсуа Вієт
Рене Декарт

6.

Квадратним рівнянням називається рівняння
2
виду:
ах вх с 0
де а, в, с це числа, х – змінна.
Якщо а = 1, то таке рівняння називається зведеним
квадратним рівнянням.

7. Назвіть в квадратному рівнянні його коефіцієнти.

1) 5x²-9x+4=0
2) x²+3x-10=0
3) -x²-8x+1=0
4) -4x²+5x=0
5) 6x²-30=0
6) 9x²=0

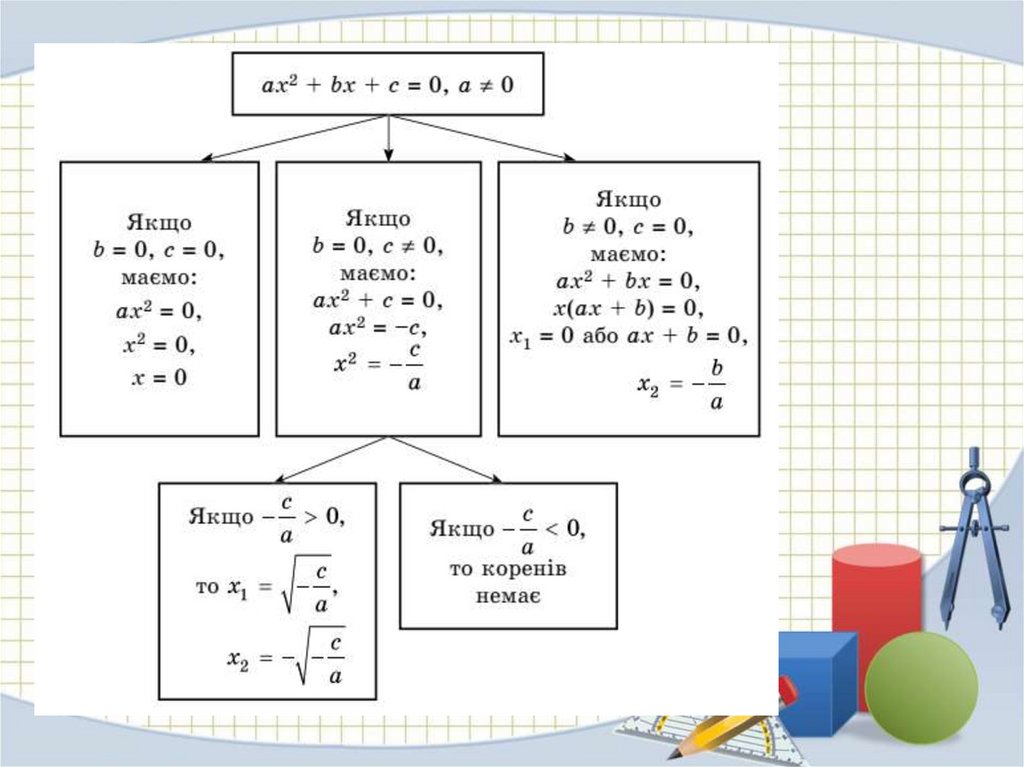
8.

ах вх 0;
2
ах с 0;
2
ах 0.
2

9.

10.

11. Рівняння виду

Рівняння
2
ax
0
виду
2
рівносильне рівнянню x 0
І тому завжди має тільки
один корінь
Приклади
x 0
4x 0
2
x 0
x 0
2
3 2
x 0
5
2
x 0
x 0

12.

Рівняння
2
ax bx 0
виду
розв'язується винесенням за
дужки
2
x 0 _ або _ ax b 0
ax bx 0
x(ax b) 0
Приклади
2 x 2 3x 0
x(2 x 3) 0
x 0
або
2x 3 0
2x 3
x 1,5
Відповідь : x1 0; x2 1,5.
b
x1 0 _ або _ x2
a
x 2 0,5 x 0
x( x 0,5) 0
x 0
або
x 0,5 0
x 0,5
Відповідь : x1 0; x2 0,5.

13.

Рівняння
виду
рівносильне
рівнянню
ax с
2
c
2
x
a
c
Якщо 0,
a
то рівняння
коренів не
має
c
Якщо
a
x1, 2
ax 2 с 0
ax с
2
Приклади
7 x 28 0
4 x 2 16 0
7 x 28
4 x 2 16
x 4
x 2 4
x1, 2 4
Відповідь: рівняння
коренів не має
2
2
2
x1, 2 2
0, то
c
a
Відповідь : 2.

14.

15.

16.

• Повним квадратним рівнянням називається
таке рівняння, у якому жодний з коефіцієнтів a,
b, c не дорівнює нулю.
• Повні квадратні рівняння розв’язуються за
допомогою дискримінанту
(лат. diskriminans — розрізняючий), який
позначається латинською літерою D.
ax bx c 0
2
D b 4ac
2

17. Розв’язування повних квадратних рівнянь

За формулою коренів квадратного рівняння
ax2+bx+c=0,
b D
X 1, 2
2a
, де D=b2-4ac

18.

Вираз b²-4ac називається
дискримінантом квадратного рівняння
якщо D>0 - 2 корені,
якщо D=0 - 1 корінь,
якщо D<0 – немає коренів

19.

20. Запам'ятайте!

Теорема Вієта:
Якщо зведене квадратне рівняння х²+pх+q=0
має два корені, то їх сума дорівнює другому
коефіцієнту рівняння, взятому з
протилежним знаком,
а добуток – вільному члену.
Тобто: х₁+х₂= - p;
х₁·х₂= q.

21. Запам'ятайте!

Теорема (обернена до теореми Вієта):
Якщо сума і добуток чисел m і n
дорівнюють відповідно - p і q,
то m і n – корені рівняння х²+pх+q=0.
Користуючись оберненою теоремою Вієта, можна
перевірити, чи є та чи інша пара чисел коренями
зведеного квадратного рівняння.
Це дає змогу усно розв'язувати
такі
рівняння.

22. Виконайте усно:

Перевірте чи є дані числа коренями
рівняння:
х² – 5х + 6 = 0, 2 і 3
х² – х – 6 = 0, -3 і -2
х² + х – 6 = 0, -3 і 2
х² + 5х – 6 = 0, -1 і 6
х² – 2х – 3 = 0, 1 і -3
х² + 4х + 5 = 0, -5 і -1
х² + 3х – 10 = 0, 2 і -5

23. Виконайте усно:

Знайдіть суму і добуток коренів
рівняння:
х² – 3х + 2 = 0
х² + 5х + 6 = 0
х² – х – 2 = 0
х² + х – 2 = 0
х² + 6х + 5 = 0
х² – 6х + 5 = 0
х² – 4х – 5 = 0
х² – 7х + 6 = 0

24. Поміркуйте!

25. Виконаємо разом. Розв'яжіть рівняння:

26. Виконаємо разом:

Розв'яжіть рівняння:
х² + 4х – 5 = 0
х² – 4х + 3 = 0
х² + 2х – 3 = 0
х² + 4х + 3 = 0
х² + 3х + 2 = 0
х² – х – 12 = 0
х² –3х –10 = 0

27. Виконаємо разом:

Рівняння х²+pх+q=0 має два корені 0,7 і 10.
Знайдіть його коефіцієнти p і q.
Розв'язання: за теоремою Вієта:
p = - (0,7+10) = -10,7; q = 0,7·10 = 7.
Відповідь: q =7; p = - 10,7.
Знайдіть p і х₁, якщо х²+pх-21=0 і х₂=-3.
Розв'язання: за теоремою Вієта:
q = х₁ ·(-3) = -3 х₁ = -21,
звідси х₁ =-21:(-3)=7
p = - (х₁-3) = 3- х₁=3-7= -4.
Відповідь: х₁=7; p =-4.

28. Зверніть увагу!

Теорему Вієта застосовують лише до
зведених квадратних рівнянь.
Інколи вам не буде вдаватися за
теоремою Вієта розв'язати зведене
квадратне рівняння. Причиною цього
можуть бути дробові числа або взагалі
відсутність розв'язку рівняння.
В такому випадку варто перевірити
дискримінант цього рівняння,
або ж навіть розв'язати його
за дискримінантом.

29. Д/З: опрацювати презентацію Розв’язати рівняння: 1) 2) 4х2 – 8х = 0; 3) 16х2 = 0; 4) 2х2 – 50 = 0 5) Рівняння Х2 + рХ + 24 = 0

Д/З: опрацювати презентацію
Розв’язати рівняння:
1)
2) 4х2 – 8х = 0;
3) 16х2 = 0;
4) 2х2 – 50 = 0
5) Рівняння Х2 + рХ + 24 = 0
має корінь Х1 = 8.
Знайти р і другий корінь.

30.

До зустрічі!