Использование графов при решении задач ОГЭ по информатике (9 класс)

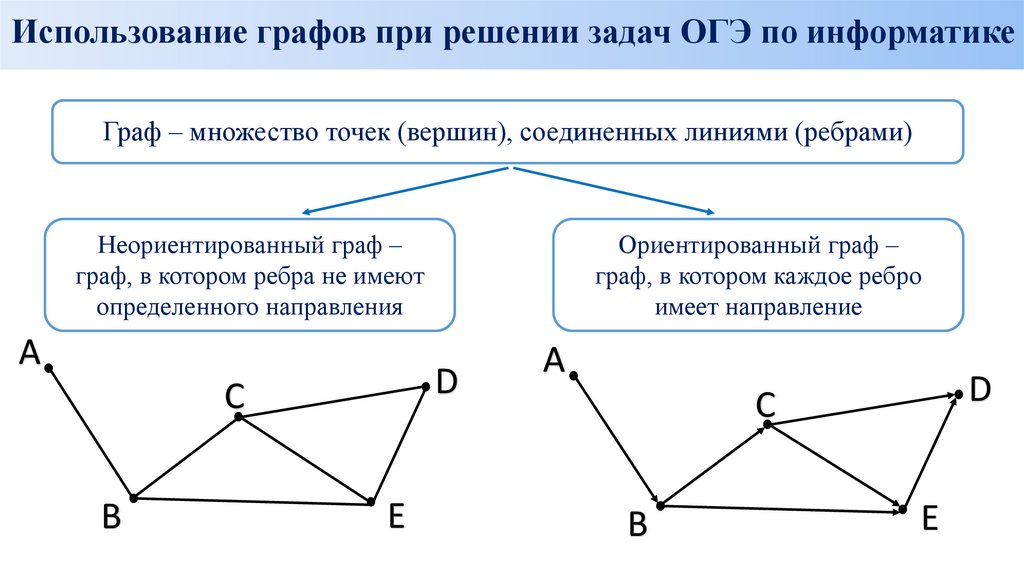
1. Граф – множество точек (вершин), соединенных линиями (ребрами)

Использование графов при решении задач ОГЭ по информатике
Граф – множество точек (вершин), соединенных линиями (ребрами)
Неориентированный граф –
граф, в котором ребра не имеют
определенного направления
A
D
C
B
Ориентированный граф –
граф, в котором каждое ребро
имеет направление
E
A
D
C
B
E

2.

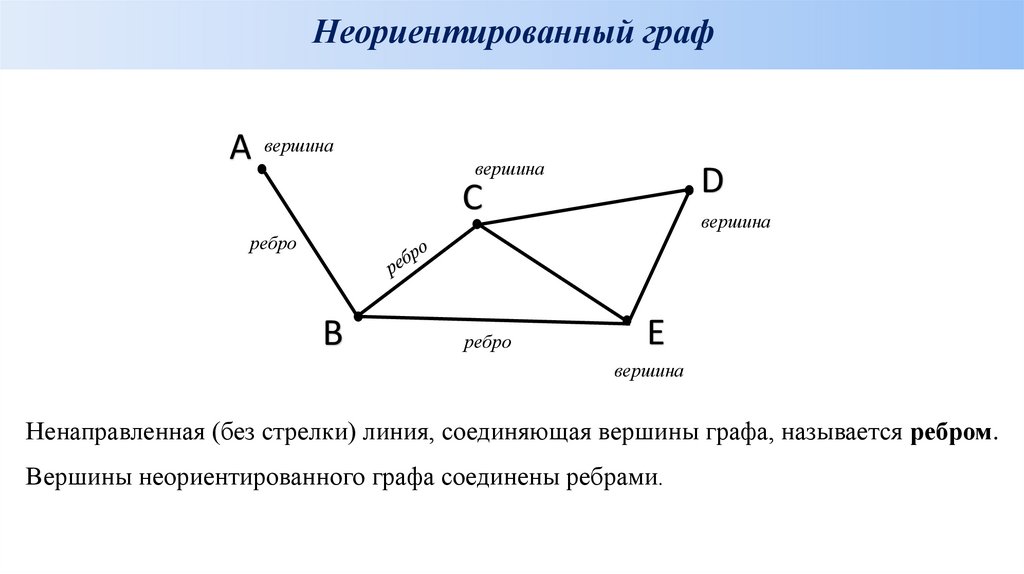
Неориентированный граф
A вершина
вершина
D
C
вершина
ребро
B
ребро
E
вершина
Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром.
Вершины неориентированного графа соединены ребрами.

3.

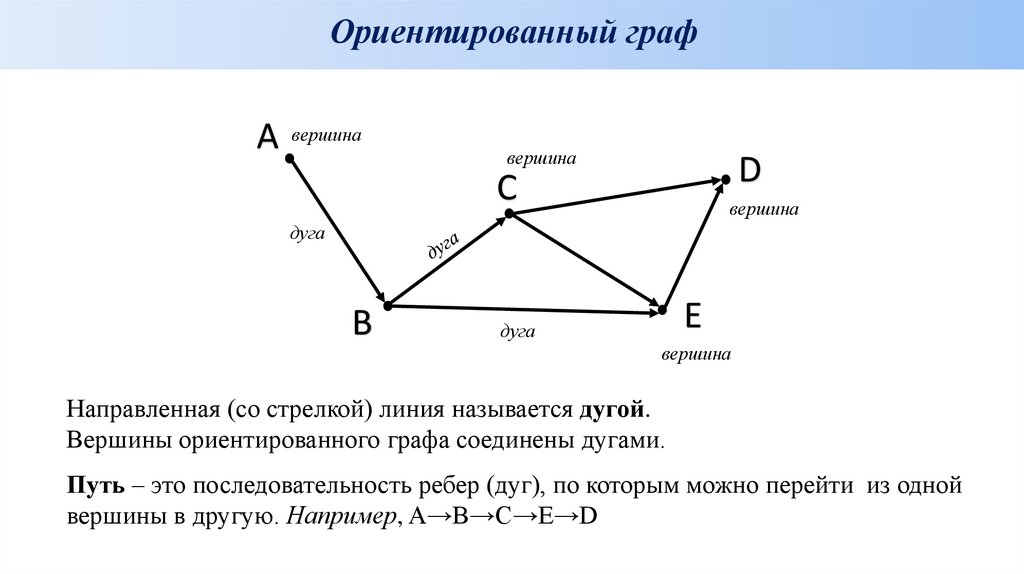
Ориентированный граф
A вершина
вершина
D
C
вершина
дуга
B
E
дуга
вершина
Направленная (со стрелкой) линия называется дугой.
Вершины ориентированного графа соединены дугами.
Путь – это последовательность ребер (дуг), по которым можно перейти из одной
вершины в другую. Например, A→B→C→E→D

4.

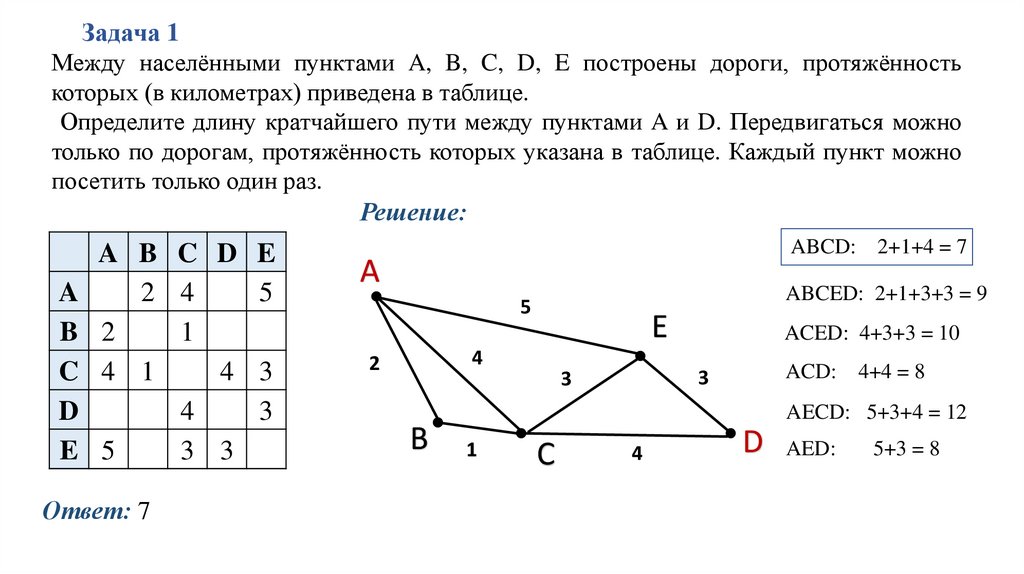
Задача 1
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость
которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и D. Передвигаться можно
только по дорогам, протяжённость которых указана в таблице. Каждый пункт можно
посетить только один раз.
Решение:
A B
A
2
B 2
C 4 1
D
E 5
Ответ: 7
C D
4
1
4
4
3 3
E
5
3
3
ABCD: 2+1+4 = 7
А
ABCED: 2+1+3+3 = 9
5
E
4
2
ACED: 4+3+3 = 10
3
3
ACD:
4+4 = 8
AECD: 5+3+4 = 12
B
1
C
4
D AED:
5+3 = 8

5.

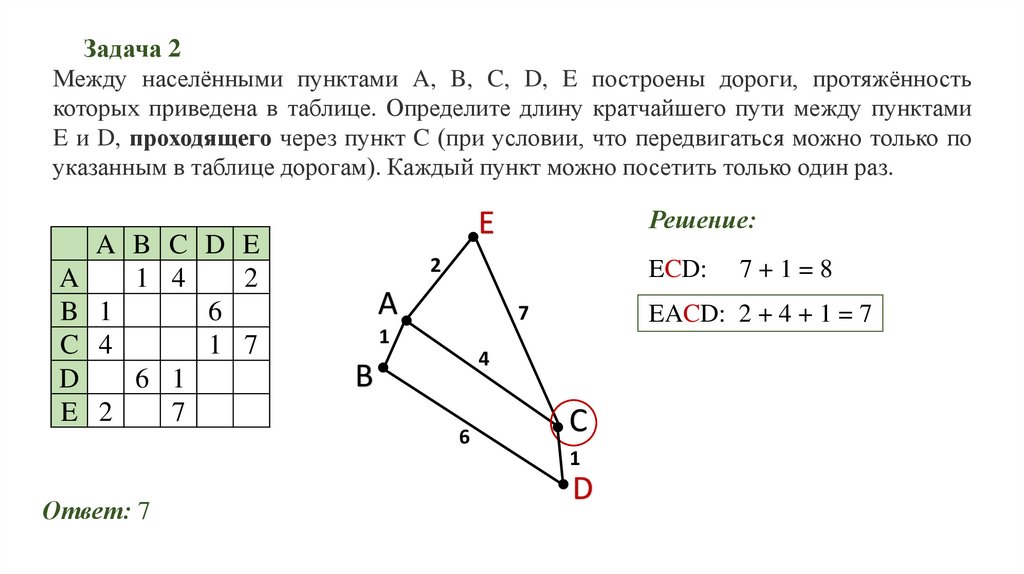
Задача 2
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость
которых приведена в таблице. Определите длину кратчайшего пути между пунктами
E и D, проходящего через пункт C (при условии, что передвигаться можно только по
указанным в таблице дорогам). Каждый пункт можно посетить только один раз.
A B C D E
A
1 4
2
B 1
6
C 4
1 7
D
6 1
E 2
7
Решение:
E
2
ECD:
А
7
EACD: 2 + 4 + 1 = 7
1
4
B
6
C
1
Ответ: 7
7+1=8
D

6.

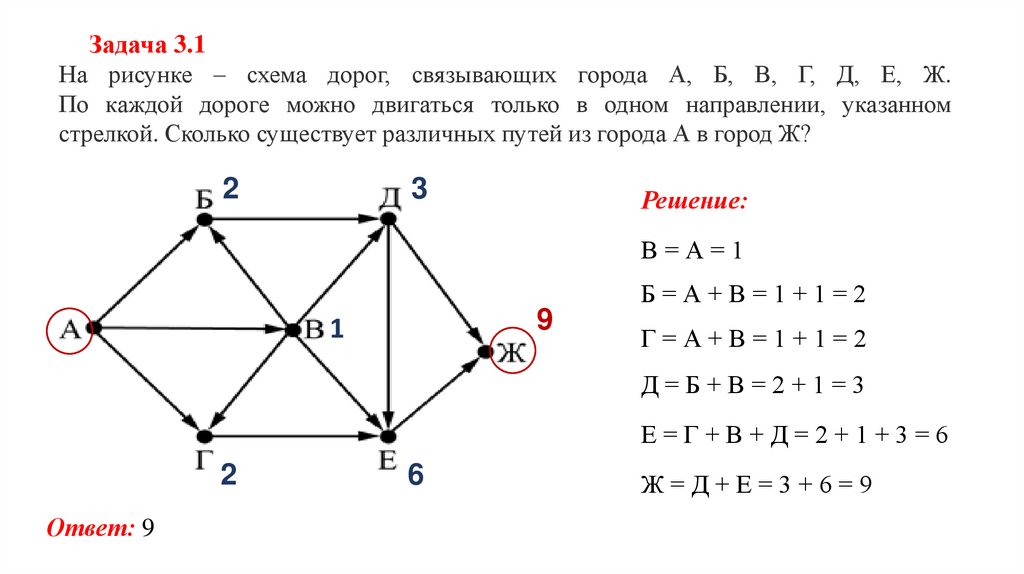
Задача 3.1
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж.
По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Ж?
2
3
Решение:
В=А=1
Б=А+В=1+1=2
9
1
Г=А+В=1+1=2
Д=Б+В=2+1=3
Е=Г+В+Д=2+1+3=6
2
Ответ: 9
6
Ж=Д+Е=3+6=9

7.

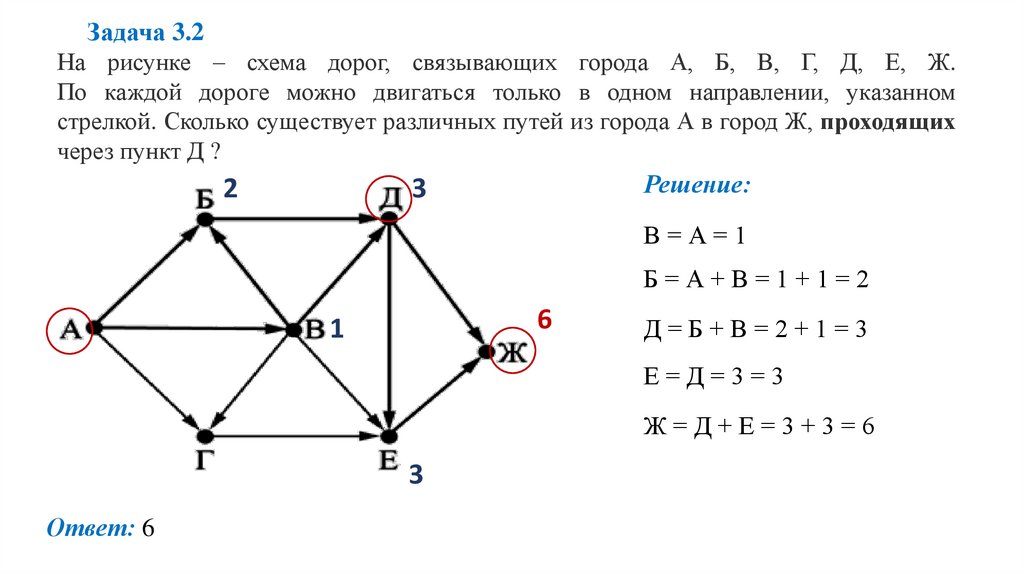
Задача 3.2
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж.
По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Ж, проходящих
через пункт Д ?
Решение:
2
3
В=А=1
Б=А+В=1+1=2
6
1
Д=Б+В=2+1=3
Е=Д=3=3
Ж=Д+Е=3+3=6
3
Ответ: 6

8.

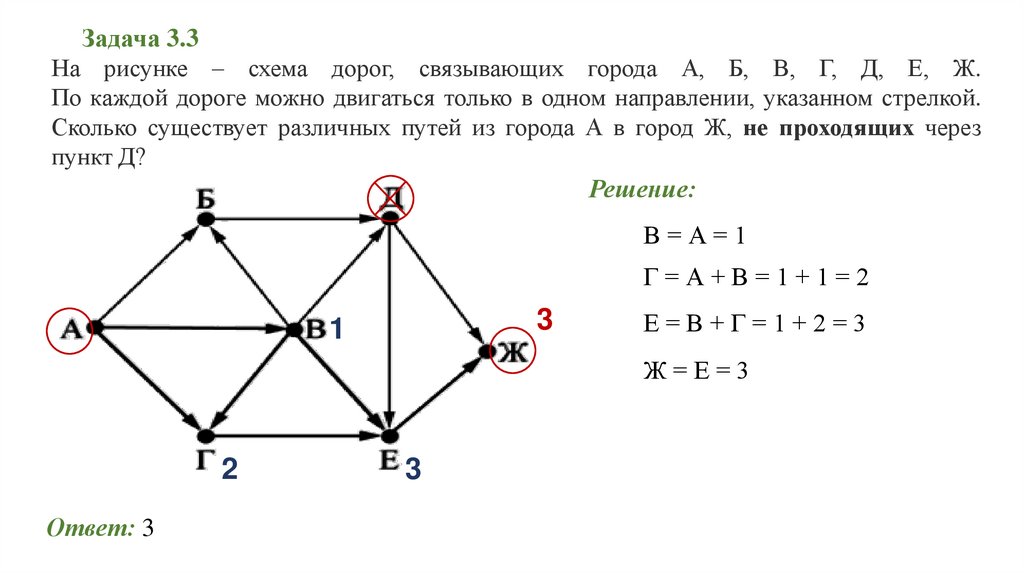
Задача 3.3
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Ж, не проходящих через
пункт Д?
Решение:
В=А=1
Г=А+В=1+1=2
3
1
Е=В+Г=1+2=3
Ж=Е=3
2
Ответ: 3
3

9. Используемая литература: 1. Босова Л.Л., Босова А.Ю. Информатика. 9 класс: учебник. – М., Просвещение, 2022. 2. Образовательный

портал для подготовки к экзаменам Сдам ГИА: Решу ОГЭ
(https://inf-oge.sdamgia.ru/)
3. Открытый банк заданий ОГЭ | Информатика
(https://oge.fipi.ru/bank/index.php)