Similar presentations:
Анимация по щелчку мыши. ОГЭ по информатике. Задание 9
1.
Анимация по щелчку мыши, Esc – выходОГЭ по информатике
Часть 1. Задание 9
2.
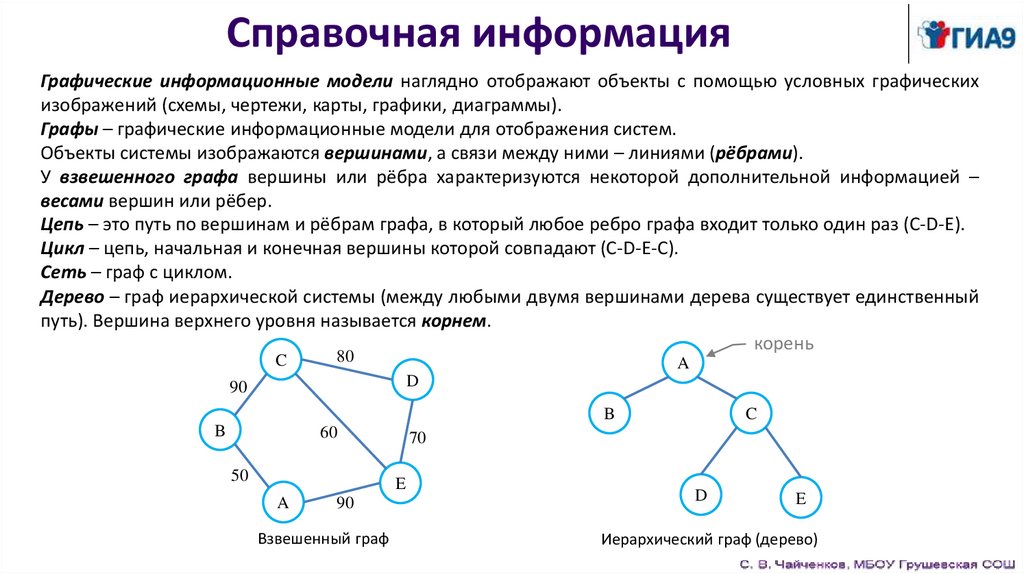
Справочная информацияГрафические информационные модели наглядно отображают объекты с помощью условных графических
изображений (схемы, чертежи, карты, графики, диаграммы).
Графы – графические информационные модели для отображения систем.
Объекты системы изображаются вершинами, а связи между ними – линиями (рёбрами).
У взвешенного графа вершины или рёбра характеризуются некоторой дополнительной информацией –
весами вершин или рёбер.
Цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит только один раз (C-D-E).
Цикл – цепь, начальная и конечная вершины которой совпадают (C-D-E-C).
Сеть – граф с циклом.
Дерево – граф иерархической системы (между любыми двумя вершинами дерева существует единственный
путь). Вершина верхнего уровня называется корнем.
корень
C
80
A
D
90
B
B
60
50
70
E
A
90
Взвешенный граф
C
D
E
Иерархический граф (дерево)
3.
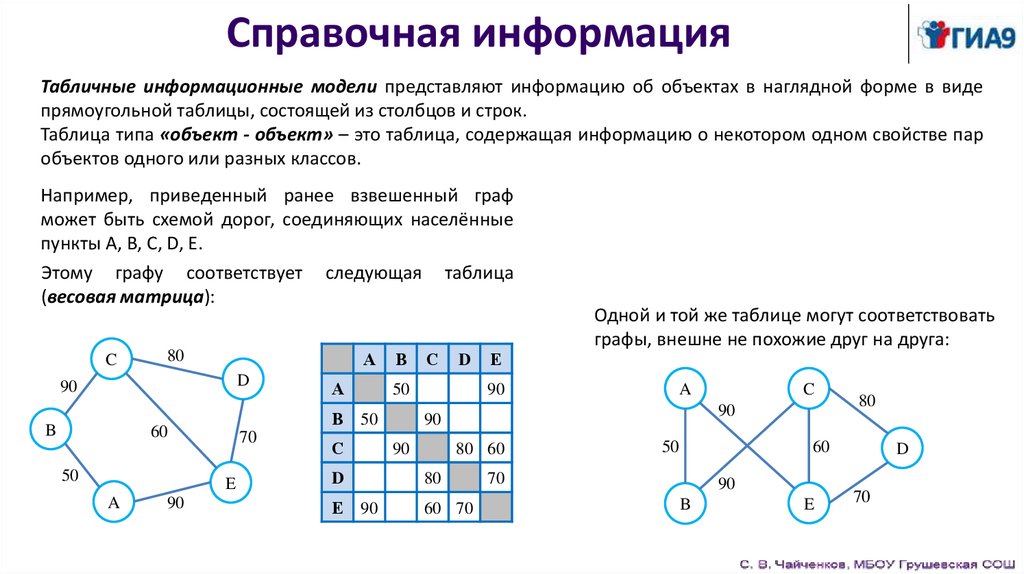
Справочная информацияТабличные информационные модели представляют информацию об объектах в наглядной форме в виде
прямоугольной таблицы, состоящей из столбцов и строк.
Таблица типа «объект - объект» – это таблица, содержащая информацию о некотором одном свойстве пар
объектов одного или разных классов.
Например, приведенный ранее взвешенный граф
может быть схемой дорог, соединяющих населённые
пункты A, B, C, D, E.
Этому графу соответствует следующая таблица
(весовая матрица):
C
80
А
D
90
B
В
60
50
70
E
A
90
А
С
D
50
50
С
A
C
90
90
80 60
80
90
Е
90
90
D
Е
В
Одной и той же таблице могут соответствовать
графы, внешне не похожие друг на друга:
60 70
50
80
60
70
90
B
E
D
70
4.
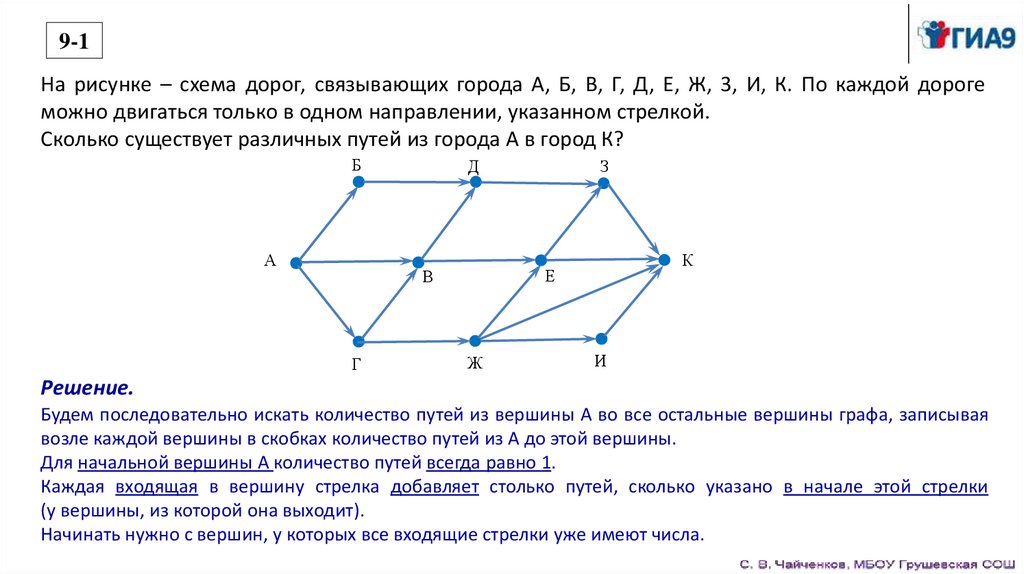
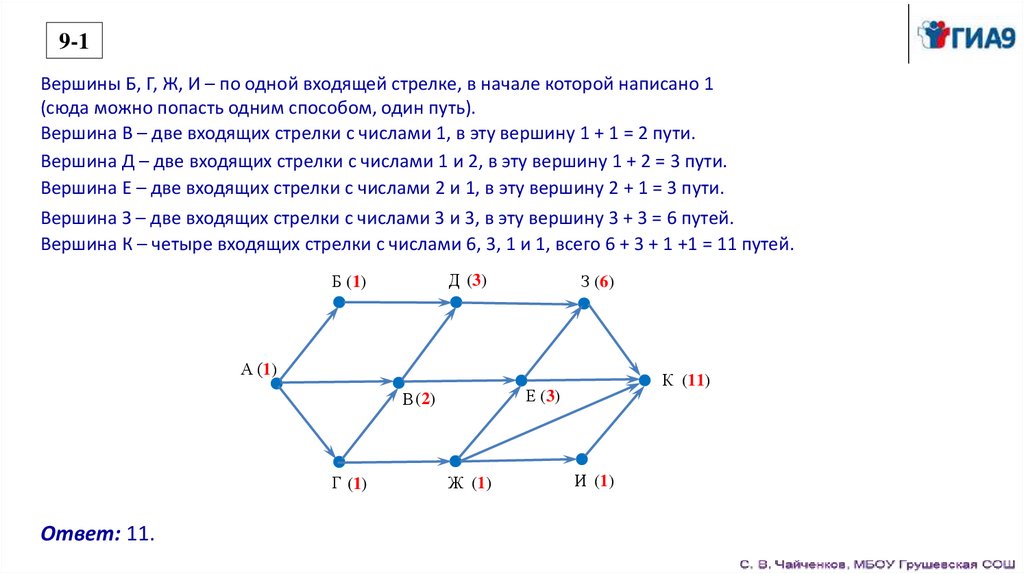
9-1На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К. По каждой дороге
можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К?
Б
А
К
Е
В
Г
З
Д
Ж
И
Решение.
Будем последовательно искать количество путей из вершины А во все остальные вершины графа, записывая
возле каждой вершины в скобках количество путей из А до этой вершины.
Для начальной вершины А количество путей всегда равно 1.
Каждая входящая в вершину стрелка добавляет столько путей, сколько указано в начале этой стрелки
(у вершины, из которой она выходит).
Начинать нужно с вершин, у которых все входящие стрелки уже имеют числа.
5.
9-1Вершины Б, Г, Ж, И – по одной входящей стрелке, в начале которой написано 1
(сюда можно попасть одним способом, один путь).
Вершина В – две входящих стрелки с числами 1, в эту вершину 1 + 1 = 2 пути.
Вершина Д – две входящих стрелки с числами 1 и 2, в эту вершину 1 + 2 = 3 пути.
Вершина Е – две входящих стрелки с числами 2 и 1, в эту вершину 2 + 1 = 3 пути.
Вершина З – две входящих стрелки с числами 3 и 3, в эту вершину 3 + 3 = 6 путей.
Вершина К – четыре входящих стрелки с числами 6, 3, 1 и 1, всего 6 + 3 + 1 +1 = 11 путей.
Д (3)
Б (1)
З (6)
А (1)
В (2)
Г (1)
Ответ: 11.
К (11)
Е (3)
Ж (1)
И (1)
6.
9-2На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и З. По каждой дороге можно
двигаться только в одном направлении, указанном стрелкой. Сколько существует различных
путей из города А в город З, проходящих через город В?
Б
Б
Д
А
Е
В
Г
Ж
З
Д
А
Е
В
Г
Ж
Решение.
По условию задачи нужно найти только пути, проходящие через город В.
Поэтому нужно вычеркнуть на схеме те стрелки пути, которые не идут через вершину В.
З
7.
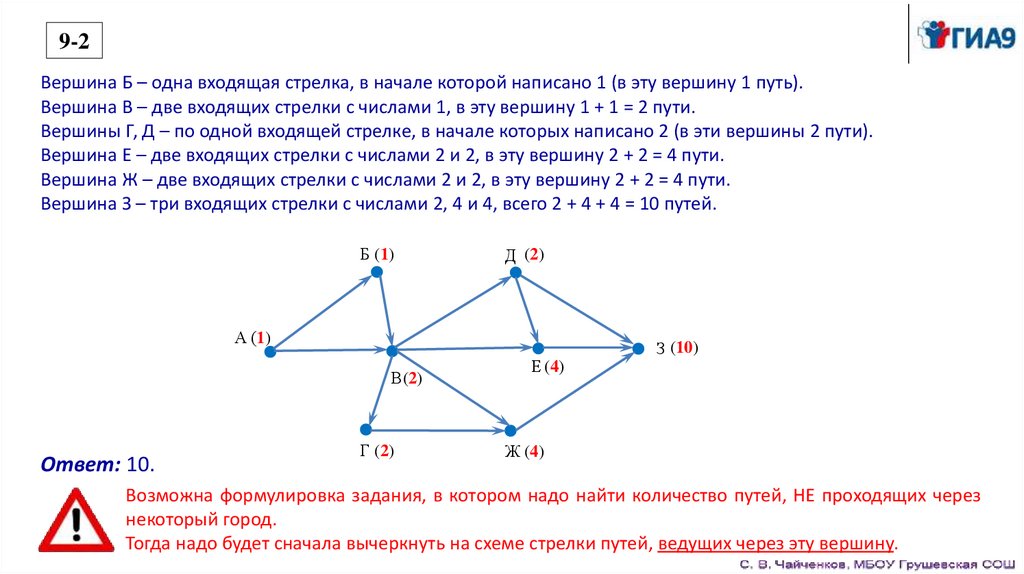
9-2Вершина Б – одна входящая стрелка, в начале которой написано 1 (в эту вершину 1 путь).
Вершина В – две входящих стрелки с числами 1, в эту вершину 1 + 1 = 2 пути.
Вершины Г, Д – по одной входящей стрелке, в начале которых написано 2 (в эти вершины 2 пути).
Вершина Е – две входящих стрелки с числами 2 и 2, в эту вершину 2 + 2 = 4 пути.
Вершина Ж – две входящих стрелки с числами 2 и 2, в эту вершину 2 + 2 = 4 пути.
Вершина З – три входящих стрелки с числами 2, 4 и 4, всего 2 + 4 + 4 = 10 путей.
Б (1)
Д (2)
А (1)
В (2)
Ответ: 10.
Г (2)
Е (4)
З (10)
Ж (4)
Возможна формулировка задания, в котором надо найти количество путей, НЕ проходящих через
некоторый город.
Тогда надо будет сначала вычеркнуть на схеме стрелки путей, ведущих через эту вершину.
8.
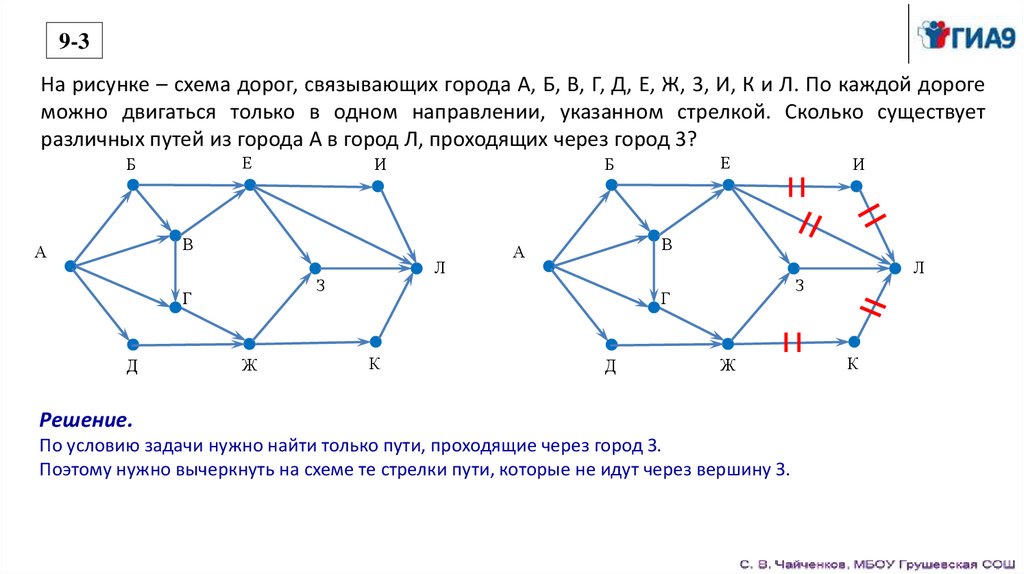
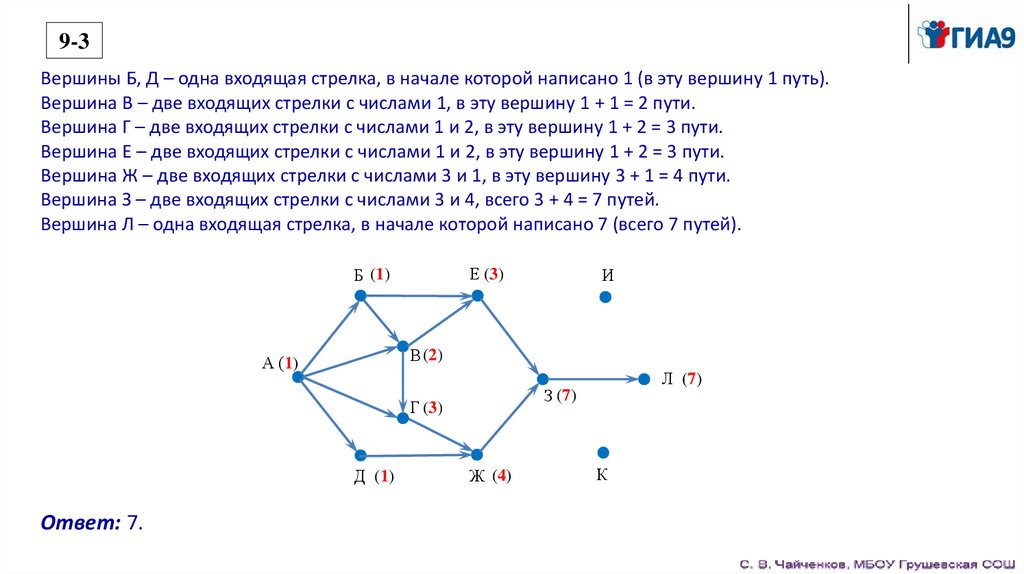
9-3На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К и Л. По каждой дороге
можно двигаться только в одном направлении, указанном стрелкой. Сколько существует
различных путей из города А в город Л, проходящих через город 3?
Е
Б
В
А
Г
Д
Л
З
Ж
Е
Б
И
В
А
Д
Л
З
Г
К
И
Ж
Решение.
По условию задачи нужно найти только пути, проходящие через город З.
Поэтому нужно вычеркнуть на схеме те стрелки пути, которые не идут через вершину З.
К
9.
9-3Вершины Б, Д – одна входящая стрелка, в начале которой написано 1 (в эту вершину 1 путь).
Вершина В – две входящих стрелки с числами 1, в эту вершину 1 + 1 = 2 пути.
Вершина Г – две входящих стрелки с числами 1 и 2, в эту вершину 1 + 2 = 3 пути.
Вершина Е – две входящих стрелки с числами 1 и 2, в эту вершину 1 + 2 = 3 пути.
Вершина Ж – две входящих стрелки с числами 3 и 1, в эту вершину 3 + 1 = 4 пути.
Вершина З – две входящих стрелки с числами 3 и 4, всего 3 + 4 = 7 путей.
Вершина Л – одна входящая стрелка, в начале которой написано 7 (всего 7 путей).
Е (3)
Б (1)
В (2)
А (1)
Д (1)
Л (7)
З (7)
Г (3)
Ответ: 7.
И
Ж (4)
К
10.
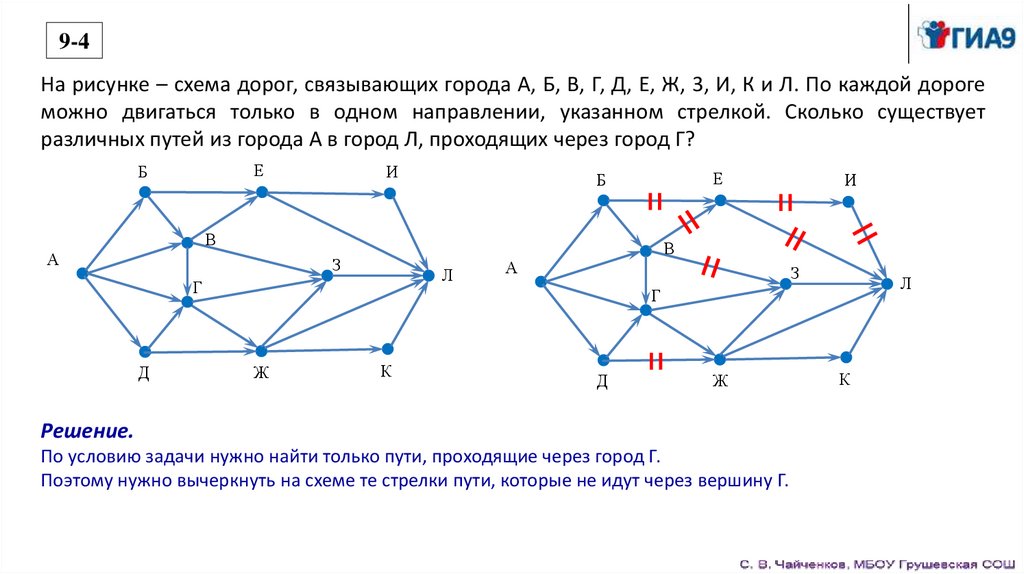
9-4На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К и Л. По каждой дороге
можно двигаться только в одном направлении, указанном стрелкой. Сколько существует
различных путей из города А в город Л, проходящих через город Г?
Е
Б
И
Е
Б
В
А
В
З
Л
Г
Д
И
А
З
Л
Г
Ж
К
Д
Ж
Решение.
По условию задачи нужно найти только пути, проходящие через город Г.
Поэтому нужно вычеркнуть на схеме те стрелки пути, которые не идут через вершину Г.
К
11.
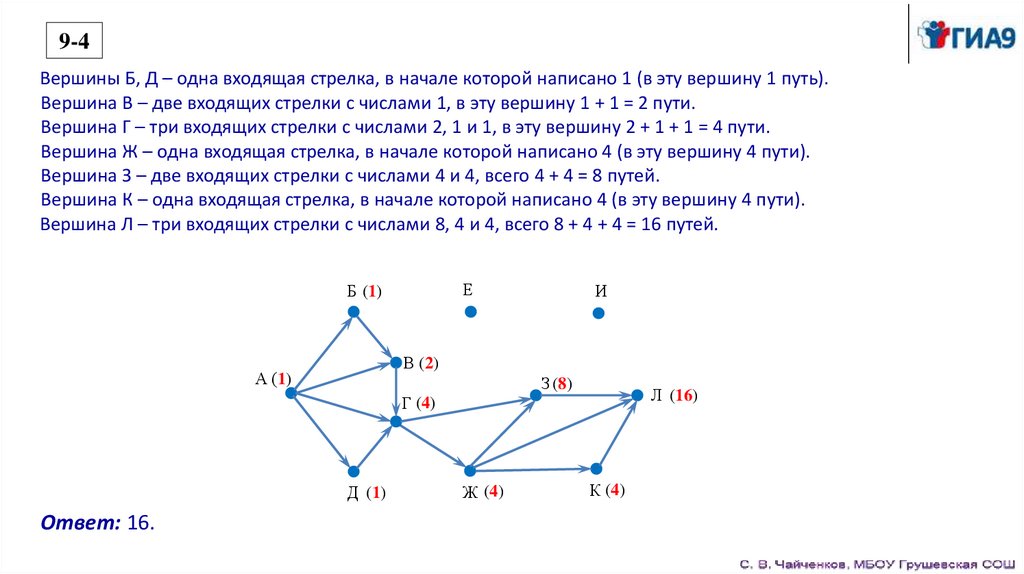
9-4Вершины Б, Д – одна входящая стрелка, в начале которой написано 1 (в эту вершину 1 путь).
Вершина В – две входящих стрелки с числами 1, в эту вершину 1 + 1 = 2 пути.
Вершина Г – три входящих стрелки с числами 2, 1 и 1, в эту вершину 2 + 1 + 1 = 4 пути.
Вершина Ж – одна входящая стрелка, в начале которой написано 4 (в эту вершину 4 пути).
Вершина З – две входящих стрелки с числами 4 и 4, всего 4 + 4 = 8 путей.
Вершина К – одна входящая стрелка, в начале которой написано 4 (в эту вершину 4 пути).
Вершина Л – три входящих стрелки с числами 8, 4 и 4, всего 8 + 4 + 4 = 16 путей.
Е
Б (1)
И
В (2)
А (1)
З (8)
Л (16)
Г (4)
Д (1)
Ответ: 16.
Ж (4)
К (4)


 informatics
informatics