Дифференциальное исчисление функции одной переменной. Программа 2 семестра

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
ПРОГРАММА 2 СЕМЕСТРА
1. Дифференциальное исчисление функции одной переменной.
2. Комплексные числа.
3. Неопределенный интеграл .
4. Определенный интеграл.
Литература
1. Шипачев В.С. Высшая математика.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления, том 2.
3. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс.
4. Берман Г. Н. Сборник задач по курсу математического анализа.
5. Математический практикум. Части 2 и 3.

2.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
Раздел: Дифференциальное исчисление функции
Лекция 1. Определение производной:
геометрический и физический смысл.
Дифференцируемость функции
18.07.2025
г. Санкт-Петербург
2025
1/15

3.

Содержание лекции
1. Задачи, приводящие к понятию производной.
2. Определение приращения функции и
производной функции
3. Связь между дифференцируемостью и
непрерывностью функции в точке.
4. Правила дифференцирования (таблица
производных элементарных функций)
2|15

4.

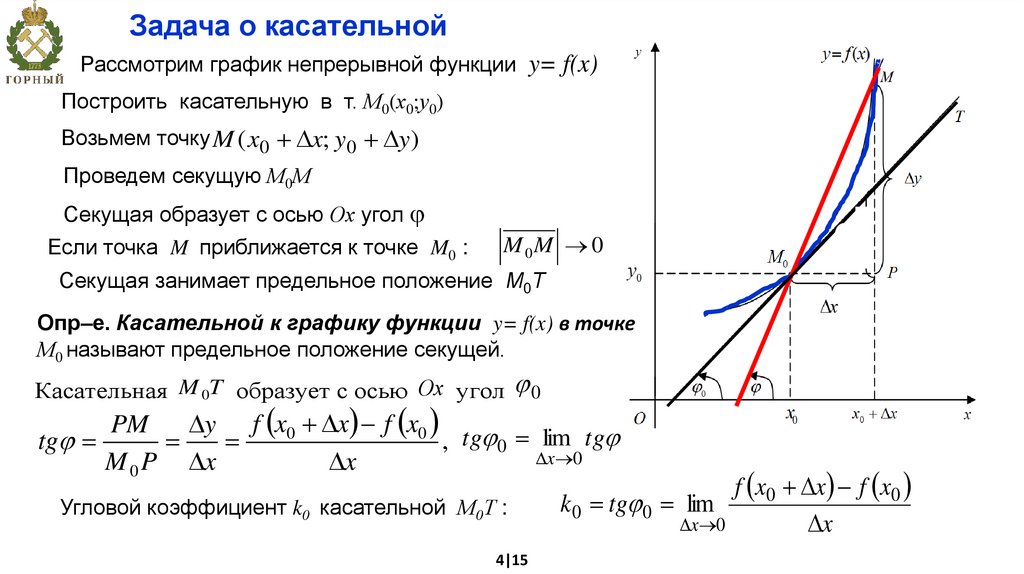
Задача о касательной
Рассмотрим график непрерывной функции y= f(x)
Построить касательную в т. М0(х0;у0)
Возьмем точку M ( x0 x; y0 y)
Проведем секущую М0М
Секущая образует с осью Ох угол
Если точка M приближается к точке M0 :
M 0M 0
Секущая занимает предельное положение М0Т
Опр–е. Касательной к графику функции y= f(x) в точке
М0 называют предельное положение секущей.
Касательная M 0T образует с осью Ох угол 0
PM
y f x0 x f x0
tg
, tg 0 lim tg
x 0
M 0 P x
x
Угловой коэффициент k0 касательной М0Т :
4|15
f x0 x f x0
k 0 tg 0 lim
x 0
x

5.

Определение
производной
Пусть функция f (x) задана на некотором промежутке Х.
Выберем х Х и дадим точке приращение х 0, чтобы х+ х Х.
Приращение функции f (x) в точке х,
соответствующее приращению аргумента х :
Разностное отношение функции:
y f x x f x
y f x x f x
x
x
Если существует конечный предел отношения приращения функции y
к приращению аргумента х при условии, что х 0, то он называется
производной функции у=f (x) по переменной х:
y
f x x f x
y х f x lim
lim
.
x 0 x
x 0
x
y
Если функция f (x) непрерывна в точке и lim
= + (или – )
x 0 x
то говорят, что функция в точке х имеет бесконечную производную.
5|15

6.

Геометрический смысл производной функции f(x) –
угловой коэффициент касательной к графику функции в т.
М0(х0;у0)
f x0 x f x0
k0 tg 0 lim
f x0 .
x 0
x
Уравнение касательной: y y0 f ( x0 )( x x0 )
Нормаль к кривой в точке М0(х0;у0) – это прямая, перпендикулярная касательной в т. М0
Угловой коэффициент нормали в точке (условие прямых) :
Уравнение нормали:
1
y y0
( x x0 ).
f ( x0 )
Замечание
Существование производной f (x )
в точке x
существование касательной к кривой
y f (x) в этой точке
Производная конечна касательная не параллельна оси Оу;
Производная бесконечна касательная параллельна оси Оу.
6|15
1
kн
k0

7.

Физический смысл производной
путь за время t
Задача о скорости материальной точки
Пусть материальная точка движется неравномерно
вдоль оси Ох по закону х=f(t)
В момент времени t
x
Средняя скорость Vср
t
Мгновенная скорость точки в момент времени t
f (t t ) f (t )
Vмгн lim Vср lim
f (t )
при прямолинейном неравномерном движении:
t 0
t 0
t
Дифференцируемость
функции
Если функция у=f (x) имеет конечную производную в точке х0
y
т.е. существует конечный lim
x 0 x
f (x) дифференциеуема в точке
, то функция называется дифференцируемой в точке.
y А x ( x) x
этой точке
( у 0) , где число А f (x) не зависит от x ;
( x) – б.м.ф. при x 0
приращение
6|15
в

8.

Связь между непрерывностью и дифференцируемостью функции
.
Теорема 1. Если функция y f (x) дифференцируема в точке x0 , то она непрерывна в этой точке
Доказательство.
y
f ( x)
Пусть функция y f (x) дифференцируема в некоторой точке x lim
x 0 x
y
x f ( x) ( x)
( x) 0 при x 0
y f ( x) x ( x) x lim y 0
x 0
функция f (x)
непрерывна в т. х
Замечание. Обратное утверждение неверно:
из непрерывности функции в некоторой точке не следует ее дифференцируемость в этой точке
График функции f (x) ,
которая имеет бесконечную
производную в т. М0
График функции,
производная которой не
существует в точке
Касательная: х=0
Нет касательной
7|15
существует
конечный
предел

9.

Правила дифференцирования
Теорема 2. Если функции u u (x) и v v(x) дифференцируемы в точке x , то:
1.
(u v) u v
2.
Производная постоянной
у c const у=0
2.1. (c f ) c f
(u v) u v uv
y
y
0
0 lim
x 0 x
x
3. u u v uv
2
v
v
(c ) 0
2.2. (u v w) u vw uv w uvw
Производные элементарных функций
у x у = х y 1 lim y 1 ( х ) 1
x
x 0 x
Степенная функция
у xn
x
n
x х х
x nx
n
8|15
n 1
v( x) 0
Cv
C
3.1. 2
v
v

10.

Показательная функция y
= ex
f ( x) e
x
f ( x x) e
y f ( x x) f ( x) e x x e x e x e x 1
x x
e
x
f ( x) ln x
x
x
y
e
e
1
x
lim
lim
e 1 ~ x
x 0 x
x 0
x 0
x
e x x
lim
ex
x 0 x
Логарифмическая функция y = ln
x
e e
x
x
f ( x x) ln( x x)
x x
x
ln 1
y f ( x x) f ( x) ln( x x) ln x ln
x
x
x
ln 1
y
x / x 1
x ln 1 x ~ x
ln x lim
lim
lim
x
0
x
x
x 0 x x 0
x 0 x
x
x
9|15
1
ln x
x

11.

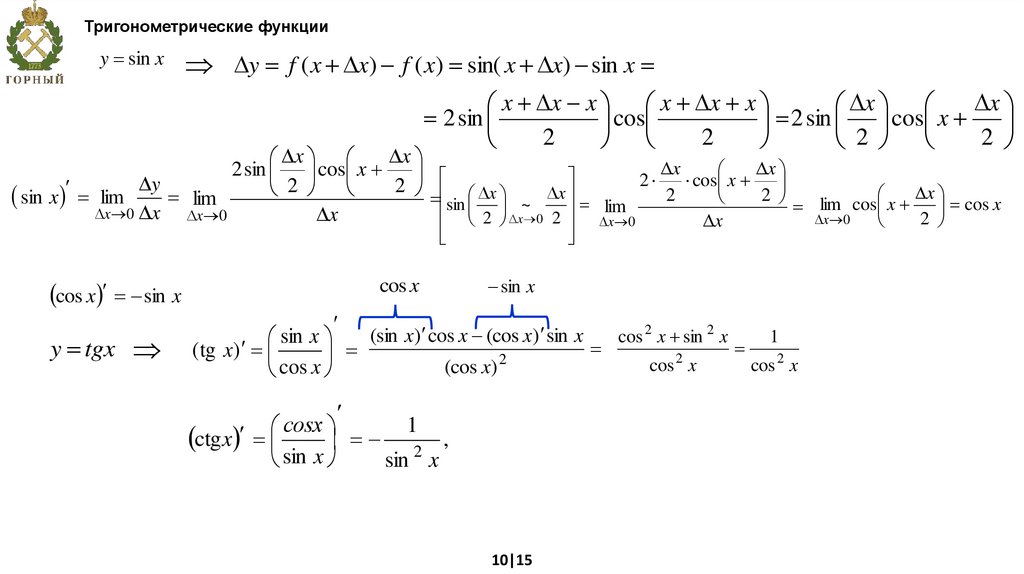
Тригонометрические функции
y sin x
y f ( x x) f ( x) sin( x x) sin x
x
x x x x x x
x
2 sin
cos
2 sin cos x
2
2
2
2
x
x
x
x
2 sin cos x
2
cos
x
y
2
2 x
x
x
2
2
sin x lim
lim
sin ~
lim
cos
x
cos x
lim
x 0 x
x 0
x
x 0
2
2 x 0 2
x 0
x
cos x sin x
y tgx
cos x
sin x
(sin x) cos x (cos x) sin x
cos 2 x sin 2 x
1
sin x
( tg x)
2
2
2
cos
x
cos
x
(cos
x
)
cos
x
сosx
1
ctgx
2 ,
sin x
sin x
10|15

12.

таблица производных
1. C 0, C - постоянная
nx
2. x
n
n 1
5.
sin x cos x
6.
cos x sin x
n N
3. e x e x
a a ln a, a 0, a 1
7.
1
4. ln x
x
log a x
8.
x
x
1
, a 0, a 1
x ln a
9. arcsin x
10. arccos x
1
11. arctgx
1 x2
1
1
,
2
1 x
12. arcctgx
1 x2
11|15
1
.
2
1 x
1
tgx 2 ,
cos x
1
ctgx 2 ,
sin x

13.

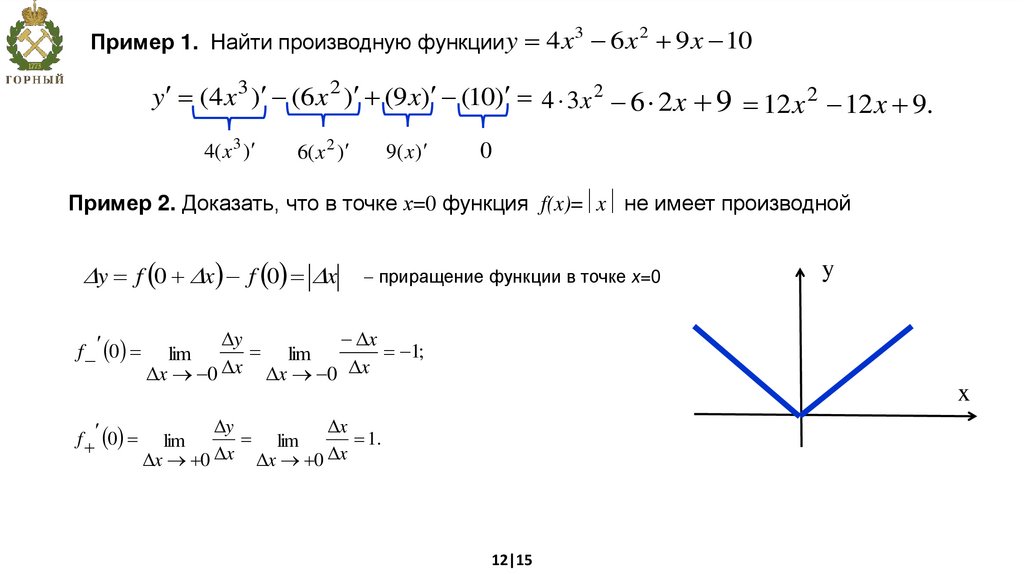
Пример 1. Найти производную функции y 4 x 6 x 9 x 10
3
2
y (4 x 3 ) (6 x 2 ) (9 x) (10) 4 3x 2 6 2x 9 12 x 2 12 x 9.
4( x 3 )
9( x )
6( x 2 )
0
Пример 2. Доказать, что в точке х=0 функция f(x)= x не имеет производной
y f 0 x f 0 x
f 0
f 0
приращение функции в точке х=0
y
x
lim
1;
lim
x 0 x x 0 x
y
x
y
x
lim
1.
lim
x 0 x x 0 x
12|15

14.

Пример 3. Вычислить производную функции
f x 3 x
в точке х=0.
y f 0 x f 0 3 x
3
lim
x 0
x
x
lim
x 0
1
3
x
2
Прямая х=0 – предельное положение секущей
f 0
Пример 5. Доказать, что функция у 3 x 2
не дифференцируема в точке х=0
f ( 0 ) lim
x 0
f(0)
lim
x 0
x
3
( x )2
1
lim 3
x
0
x
x
f (0)
1
f ( 0 ) lim
lim 3
x 0
x
0
x
x
13|15

15.

T
Пример 6. На кривой найти точку, в которой касательная к графику функции
y=4x2 6x+3 параллельна прямой y=2x.
14|15

16.

Спасибо за внимание
Санкт-Петербургский горный
университет
императрицы Екатерины II,
г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
15|15