Выпуклые функции – определение. Понятие о точке перегиба

1. Выпуклые функции – определение. Понятие о точке перегиба.

2.

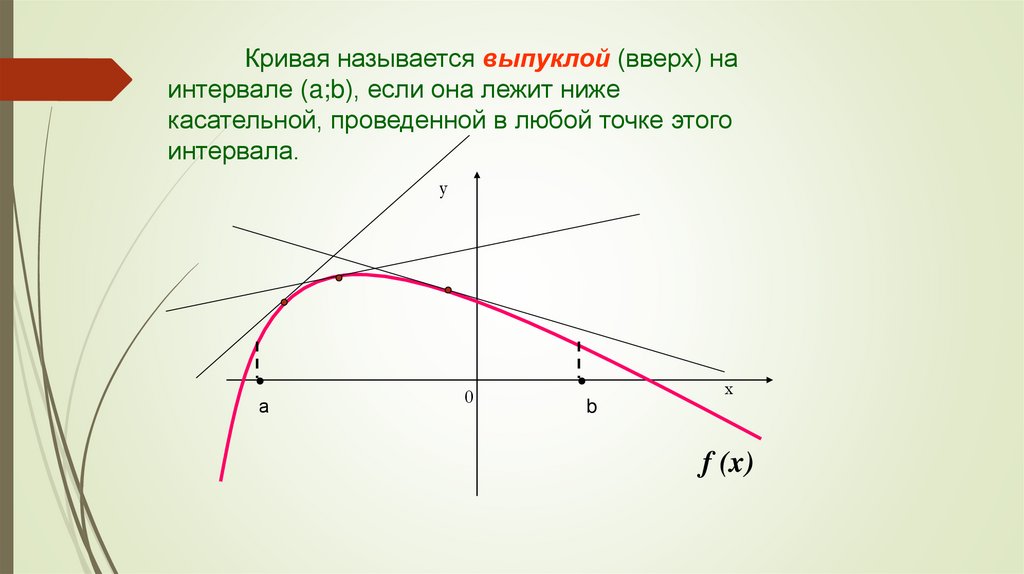
Кривая называется выпуклой (вверх) на
интервале (a;b), если она лежит ниже
касательной, проведенной в любой точке этого
интервала.
y
а
0
b
x
f (x)

3.

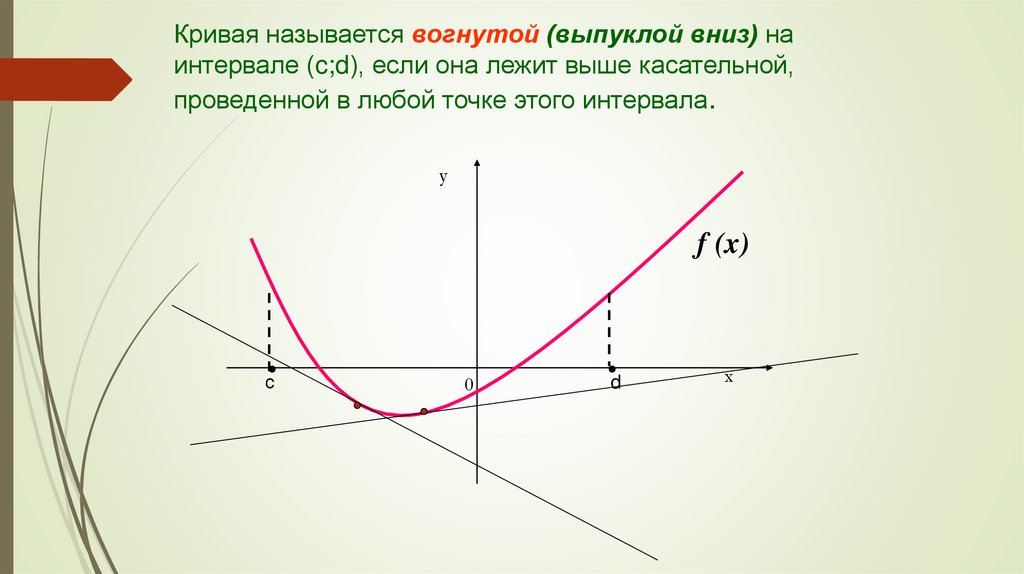
Кривая называется вогнутой (выпуклой вниз) на
интервале (c;d), если она лежит выше касательной,
проведенной в любой точке этого интервала.
y
f (x)
с
0
d
x

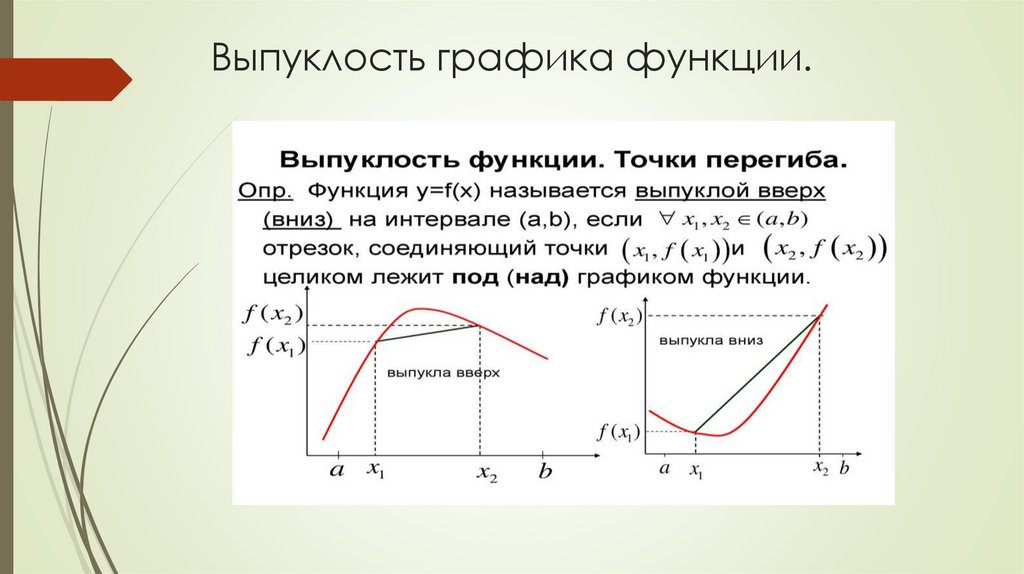
4. Выпуклость графика функции.

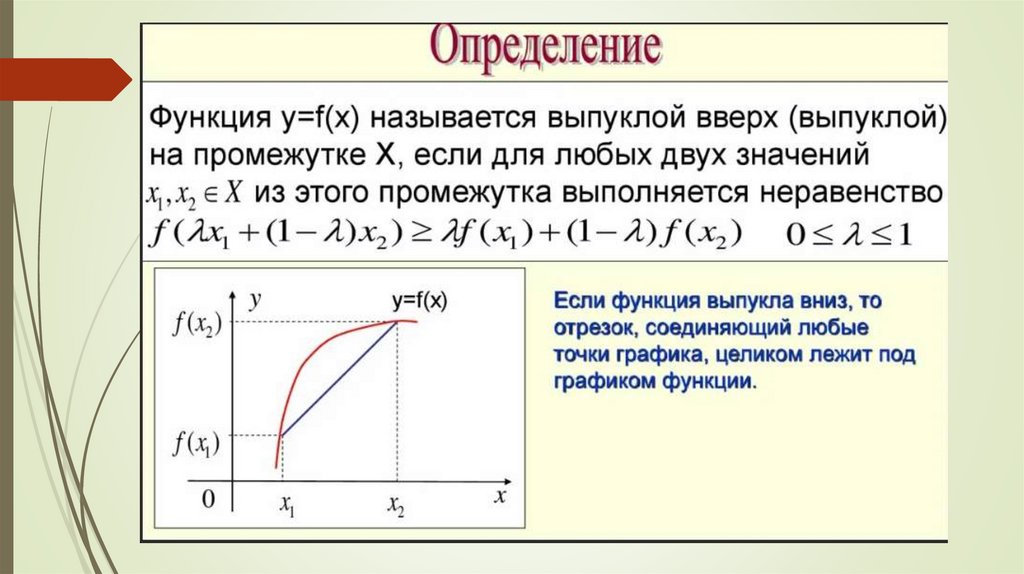
5.

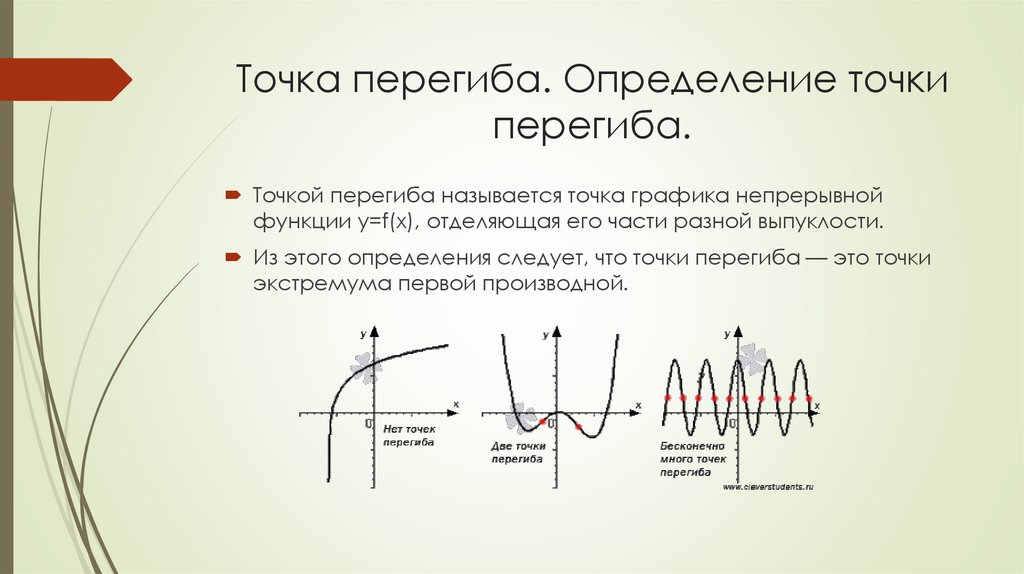
6. Точка перегиба. Определение точки перегиба.

Точкой перегиба называется точка графика непрерывной
функции y=f(x), отделяющая его части разной выпуклости.
Из этого определения следует, что точки перегиба — это точки
экстремума первой производной.

7.

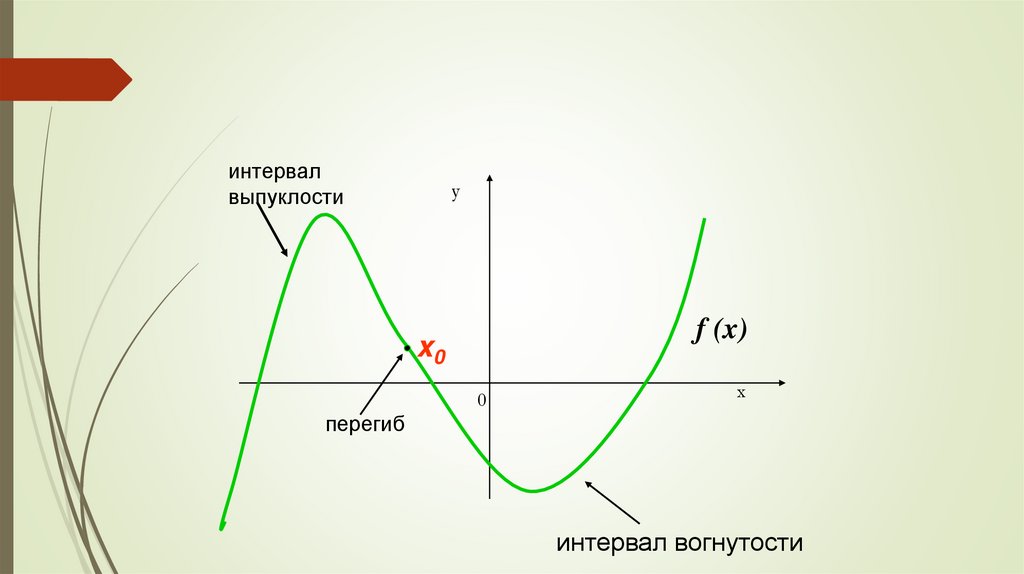
интервал
выпуклости
y
f (x)
x0
0
x
перегиб
интервал вогнутости

8. Теорема: Если функция y=f(x) во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. f″(x)<0,то график

Теорема: Если функция y=f(x) во всех точках интервала (a;b) имеет
отрицательную вторую производную, т.е. f″(x)<0,то график функции в этом
интервале выпуклый вверх. Если же f″(x)>0 ꓯx∈ (a;b)- график выпуклый вниз.
Доказательство. Пусть f″(x)<0 ꓯx∈ (a;b).
1)
Возьмем на графике функции произвольную точку М с абсциссой xₒ ∈ (a;b).
2)
Проведем через точку М касательную.
3)
Сравним в точке x∈ (a;b) ординату y кривой y=f(x) с ординатой y ее касательной.
Исследуем это равенство:

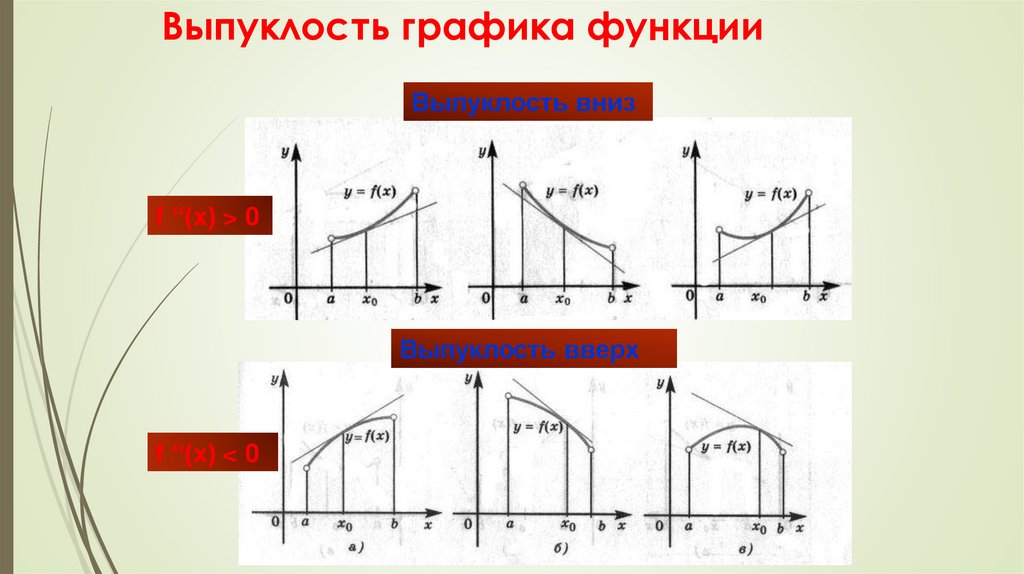
9. Выпуклость графика функции

Выпуклость вниз
f ‘‘(x) > 0
Выпуклость вверх
f ‘‘(x) < 0

10.

11.

Если точка xₒ-точка перегиба функции f(x) и если Ǝf″(x) в некоторой
окрестности точки xₒ(непрерывная в точке xₒ),то f″(xₒ)=0.
Доказательство:
Докажем методом от противного, т.е предположим, что f″(xₒ)≠0. Тогда
f″(xₒ)<0 либо f″(xₒ)>0 .
По условию f″ непрерывна в точке xₒ→по свойству сохранения знака
непрерывной функции получим :
Ǝδ:ꓯx ∈ U(δ) (xₒ), sign f″(x)= sign f″(xₒ)
т.е. по достаточному условию строгой выпуклости f″(x)>0 ꓯx ∈ (a;b)
(функция выпукла вниз) или f″(x)<0 ꓯx ∈ (a;b)(функция выпукла вверх).
Это противоречит определению точки перегиба, которое гласит, что
при переходе через точку xₒ направление выпуклости меняется.

12.

Признак точки перегиба:

13. Правило нахождения интервалов выпуклости(вогнутости) и точек перегиба

1.
2.
3.
4.
5.
6.
7.
Найти область определения функции.
Найти первую производную.
Найти вторую производную.
Найти критические точки - нули второй производной и точки
ее разрыва.
Разбить область определения на промежутки. Определить
знак f ’’(x) в полученных промежутках.
Записать интервалы выпуклости и вогнутости
Определить точки перегиба и найти значения функции в них.
РАЗОБРАТЬ ПРИМЕР