Similar presentations:
§ 15. Формула Стокса
1.
§ 15. Формула СтоксаТеорема. Если функции P x, y, z , Q x, y, z , R x, y, z
непрерывны вместе со своими частными производными первого
порядка в точках поверхности , то имеет место формула Стокса
Q P
R Q
P R
x y dxdy y z dydz z x dxdz
Pdx Qdy Rdz ,
L
где контур L – граница поверхности , причем если смотреть из
конца положительной (внешней) нормали к поверхности , то обход
по контуру должен быть виден совершающимся против хода часовой
стрелки.
Формула Стокса связывает между собой поверхностный
интеграл второго рода и криволинейный интеграл второго рода.
2.
Следствие формулы Стокса. Если выполняются условияQ P R Q P R
,
,
,
x y
y z
z x
то криволинейный интеграл по замкнутому контуру L равен нулю
Pdx Qdy Rdz 0 .
L
Пример. Вычислить
I xydx dy zdz , где контур L –
L
окружность x 2 y 2 1 , z 0 , двумя способами:
1) непосредственно, 2) используя формулу
Стокса, взяв в качестве поверхности полусферу
z 1 x 2 y 2 (рис. 1.14).
1)
Уравнение
окружности
параметрическом виде имеет вид
x cos t , y sin t , z 0, t 0; 2 .
в
Z
1
n
O
1 Y
X 1
Рисунок 1.14
3.
Используя формулуP x, y, z dx Q x, y, z dy R x, y, z dz
AB
P x t , y t , z t xt Q x t , y t , z t yt R x t , y t , z t zt dt ,
получим
2
2
2
2
2
0
0
0
0
0
I cos t sin t sin t dt cos tdt 0 dt sin 2 t cos tdt cos tdt
3
2
sin t
2
sin t 0 0 .
3 0
2) По формуле Стокса, учитывая, что P xy , Q 1 , R z ,
получим
I Pdx Qdy Rdz
L
4.
Q PR Q
P R
dxdy
dydz
dxdz
x y
z x
y z
P
R
R
Q
P
Q
0
x
0
0
0
0
y
y
x
z
z
x
0 x dxdy 0 0 dydz 0 0 dxdz xdxdy xdxdy ,
Dxy
где Dxy – проекция поверхности на плоскость OXY. Переходя к
полярным координатам x r cos и y r sin , получим
2
2
2 r
1
I r cos drd cos d r dr sin 0 0 .
3 0
Dxy
0
0
2
1
3
5.
Числовые и функциональные ряды§ 1. Числовые ряды. Сумма и сходимость ряда. Некоторые свойства
рядов. Необходимое условие сходимости. Остаток ряда. Критерий
сходимости ряда с неотрицательными членами
Числовым рядом называют выражение
u1 u 2 u3 ... u n ... ,
где u1 , u 2 ,..., u n ,... – числа, называемые членами ряда. Ряд считают заданным,
если известен общий член ряда un как функция его номера n: u n f (n) .
Сумму Sn первых n членов ряда называют n-ной частичной суммой
числового ряда
S n u1 u 2 u3 ... u n .
Пример. S1 u1 – первая частичная сумма, S 2 u1 u 2 – вторая частичная
сумма, S3 u1 u 2 u3 – третья частичная сумма и т.д.
Если существует конечный предел
lim S n S ,
n
то ряд называют сходящимся, а число S называют суммой ряда.
Если конечный предел lim S n не существует или равен бесконечности, то
n
ряд называют расходящимся.
6.
1 1 11
... п ...
2 4 8
2
Ряд сходится, так как представляет собой бесконечно
1
убывающую геометрическую прогрессию со знаменателем q
и
2
1
первым членом b1 . Сумма такой геометрической прогрессии
2
равна
b1
12
S
1.
1 q 1 1 2
Следовательно, ряд сходится.
Пример. Исследовать сходимость ряда 1 1 1 1 ... 1 n 1 ...
Ряд расходится, так как последовательность его частичных сумм
имеет вид: S1 1 , S 2 0 , S 3 1 , S 4 0 и т.д. Такая
последовательность предела не имеет.
Пример. Исследовать сходимость ряда
7.
Свойства числовых рядов.1. Исключение или добавление конечного числа слагаемых не
влияет на сходимость или расходимость ряда.
2. Если сходится ряд u1 u 2 u3 ... u n ... и его сумма равна
S, то сходится ряд Cu1 Cu 2 Cu 3 ... Cu n ... , сумма которого
равна CS, C – константа.
3. Если сходятся ряды
n 1
n 1
un и v n
и их суммы соответственно равны Su и Sv, то сходятся и ряды
un vn
n 1
и их суммы соответственно равны Su Sv .
8.
Необходимое условие сходимости ряда – если ряд сходится, тообщий член ряда стремится к нулю: lim u n 0. В случае
n
невыполнении необходимого условия ряд расходится.
Необходимое условие не является достаточным для сходимости
ряда. Существуют ряды, у которых общий член ряда стремится к
нулю, а ряд расходится. Например, общий член гармонического ряда
1 1 1
1
1 ... ... стремится к нулю, а ряд расходится.
2 3 4
n
n-ным остатком Rn сходящегося числового ряда
u1 u 2 ... u n u n 1 u n 2 ...
называют сумму
Rn u n 1 u n 2 u n 3 ...
В случае сходящегося числового ряда его сумма равна
S S n Rn ,
lim Rn lim S S n S S 0 .
n
n


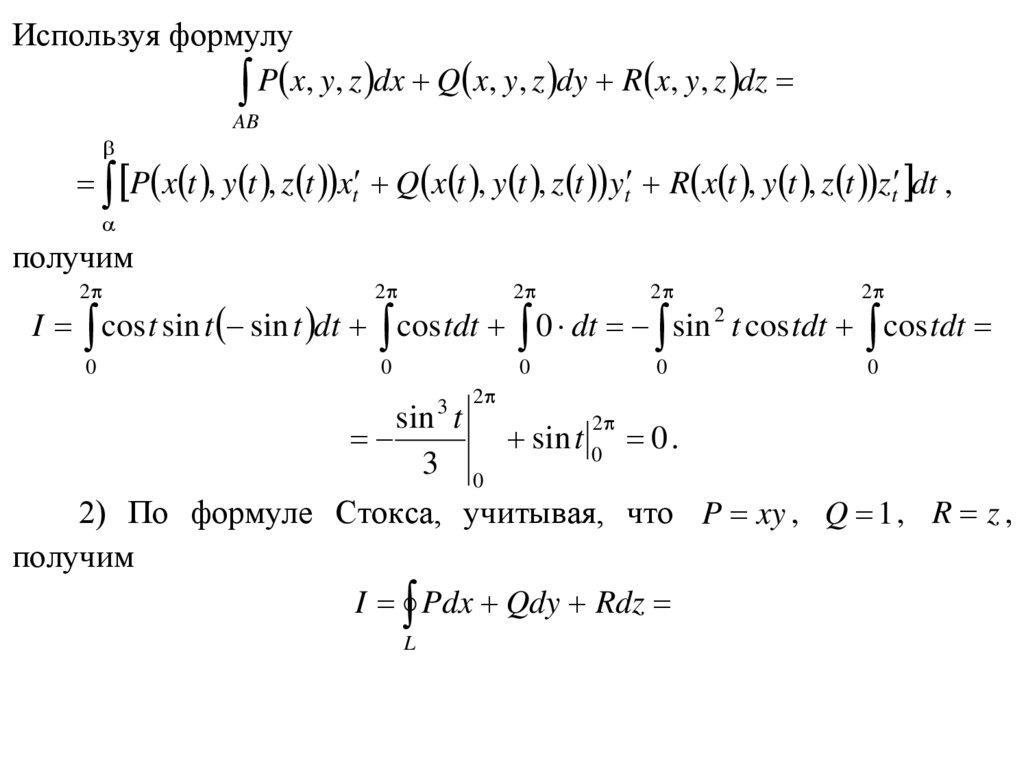





 mathematics
mathematics








