Роль математики в обеспечении точности и качества изделий на станках ЧПУ

1.

Роль математики в обеспечении
точности и качества изделий на станках
ЧПУ
Исследование ключевой роли математических расчетов в программировании и
управлении станками ЧПУ.
Тагатов Тимур Русланович

2.

Значение математических
расчетов в ЧПУ
Точность обработки зависит от правильных математических
вычислений в программах ЧПУ. Это улучшает качество
изделий, снижает брак и оптимизирует время обработки за
счёт использования G-кодов и математического
моделирования.
2

3.

Математические основы
движения инструмента на ЧПУ
Расчет траекторий инструмента
Для обеспечения точности требуется вычислять координаты
инструмента в трёхмерном пространстве с учётом его перемещений и
параметров траекторий. Особое внимание уделяется дуговым участкам
и режимам резания.
Формулы определения параметров дуги
Движение по дуге описывается формулами X = X₀ + R·cos(θ) и Y = Y₀ +
R·sin(θ), где X₀, Y₀ — центр дуги, R — радиус, а θ — угол поворота.
Используются методы интерполяции для плавного перехода между
точками.
3

4.

Круговая интерполяция в
ЧПУ: G02 и G03
01
G02 обеспечивает движение инструмента по дуге по
часовой стрелке, используя координаты конечной точки и
центра дуги (I, J) для построения точной траектории
движения.
02
G03 выполняет движение против часовой стрелки с теми
же параметрами. Вычисления учитывают направление и
обеспечивают корректное формирование криволинейных
участков обработки.
4

5.

Практический пример
программирования: обработка
прямоугольника с радиусом
В программе используется команда G42 для включения
коррекции инструмента по радиусу и G01 для линейных
перемещений к заданным координатам, что обеспечивает
точность обработки.
Команда G02 применяется для движения по дуге с заданным
центром (I5, J5). В конце G40 отключает компенсацию,
завершив точное формирование траектории инструмента.
5

6.

Важность проверки программ и симуляций в ЧПУ
Предотвращение столкновений
Симуляция позволяет заранее выявить потенциальные
механические столкновения, минимизируя риски
повреждений инструмента и заготовки.
Обнаружение ошибок вычислений
Проверка траекторий обеспечивает корректность
математических расчетов и режимов резания, что важно
для качества продукции.
Оптимизация времени обработки
Используемое программное
обеспечение
Моделирование помогает оптимизировать
технологические процессы, сокращая время обработки и
повышая производительность.
Используются CAM-системы для проектирования и
специализированные CNC-симуляторы для анализа
движения инструмента.
6

7.

Оптимизация режимов резания с использованием математических
моделей
Расчет оптимальных параметров
резания
Контроль тепловых процессов и
вибраций
Математические модели позволяют рассчитывать
оптимальную подачу, скорость вращения шпинделя и
глубину резания для повышения эффективности и
срока службы инструмента.
Использование моделей контроля тепловых и
вибрационных процессов помогает снижать износ
инструмента и улучшать качество обработки.
7

8.

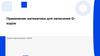
Сравнение точности обработки при использовании разных методов
интерполяции
Точность измерена координатной
измерительной машиной с высоким
разрешением, подчёркивая превосходство
круговой интерполяции.
Использование круговой интерполяции
повышает точность обработки криволинейных
элементов на 15%, снижая дефекты деталей.
8
Лабораторные исследования ЦНИИ станкостроения, 2024

9.

Основные G-коды и их математическое
содержание
Таблица представлена с описанием
функций и влияния основных G-кодов
на точность и качество обработки.
Понимание математического
содержания G-кодов критично для
повышения точности и предотвращения
ошибок.
9
Руководство по программированию станков ЧПУ, 2023

10.

Применение математической оптимизации для снижения производственного брака
Оптимальное управление и компенсация
погрешностей позволяют корректировать
траектории, снижая вероятность дефектов в
процессе обработки.
10
Автоматическое перепрограммирование с
учетом математических моделей уменьшило
производственный брак на 12%, повышая
качество и стабильность процессов.

11.

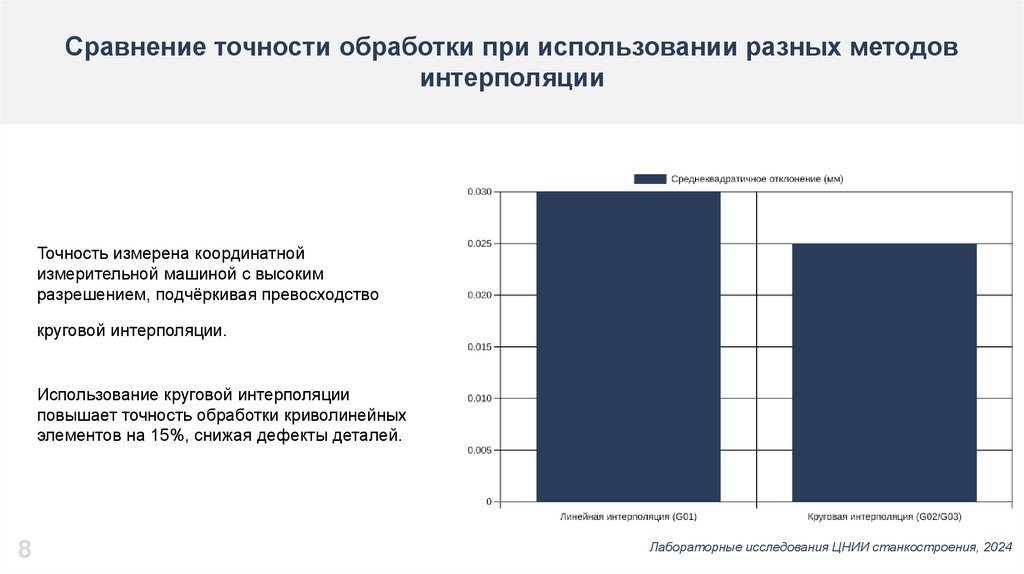
Статистика отказов и брака по причинам программирования
ЧПУ
Некорректные параметры интерполяции и
недостаток комплексной проверки увеличивают
количество дефектов, ухудшая общее качество
производства.
Ошибки в математических расчетах и
программировании считаются ведущей
причиной брака, от чего зависит эффективность
всего производственного процесса.
11
Отраслевой отчет по качеству производства деталей, 2024

12.

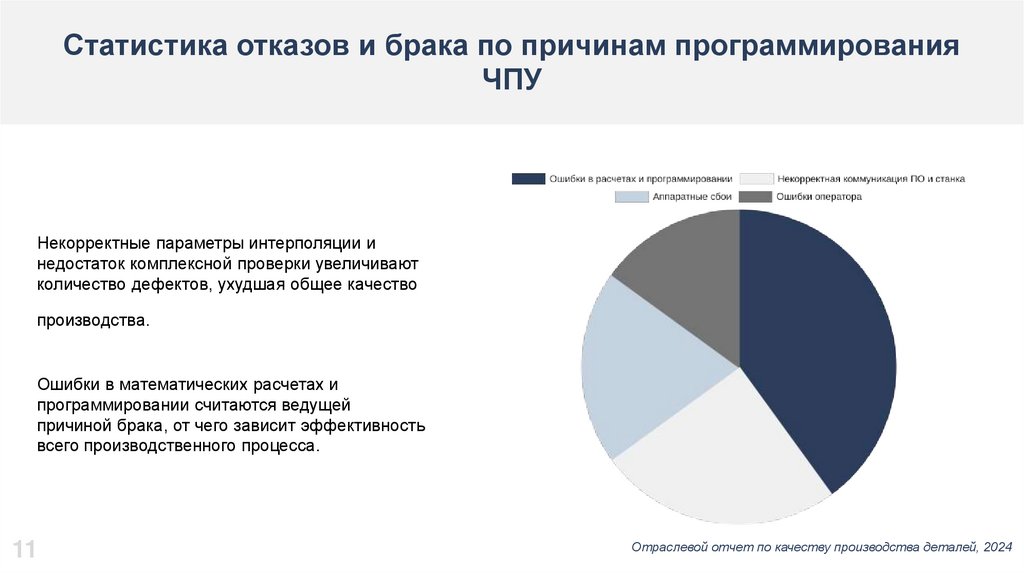
Перспективы развития математического обеспечения
станков ЧПУ
2025: Внедрение ИИ в анализ
управляющих программ
2030: Цифровые двойники для
прогнозирования качества
Использование искусственного интеллекта и машинного
обучения позволит автоматически анализировать и
оптимизировать управляющие программы, повышая
точность обработки.
Применение цифровых двойников позволит предсказывать
поведение системы в процессе обработки и качество
изделий, что повысит качество производства и снизит брак.
2028: Адаптивные модели с учётом износа
инструмента
Разработка моделей, учитывающих износ режущих инструментов и
изменяющиеся параметры станков в реальном времени, обеспечит
адаптивность технологического процесса.
12

13.

Кейс-стади: Внедрение математических
моделей на промышленном
предприятии
01
После внедрения математического моделирования
точность обработки деталей повысилась на 20%.
Сократилось время программирования на 30%,
благодаря автоматизации расчетов траекторий и
режимов резания.
02
Снижение брака составило 10%, что обусловлено
применением комплексных моделей интерполяции и
оптимизации режущих режимов. В производстве
применялись как линейные, так и круговые
математические методы.
13

14.

Рекомендации по внедрению математических методов в
ЧПУ
Обязательное обучение программистов и
операторов основам математической
интерполяции и оптимизации обеспечивает
понимание ключевых принципов точного
программирования.
Стандартизация математических моделей
для типовых операций позволяет
унифицировать процессы и ускорить
настройку станков в производстве.
14
Регулярное использование симуляторов и
автоматических систем проверки
управляющих программ снижает риски
ошибок и повышает качество обработки.
Интеграция расширенных математических
модулей в CAM-системы и
междисциплинарное сотрудничество
специалистов усиливают надежность и
точность технологического процесса.

15.

Итоги и перспективы математического
обеспечения ЧПУ
Математические методы — основа точного программирования ЧПУ. Их правильное
применение снижает уровень брака и улучшает качество изделий. Перспективы —
внедрение ИИ и адаптивных моделей для повышения эффективности и точности.