Приложения дифференциального исчисления 14. Исследование функций с помощью производных (монотонность, точки экстремума)

1. Приложения дифференциального исчисления

14. Исследование функций с
помощью производных
(монотонность, точки экстремума)

2. Монотонность функций

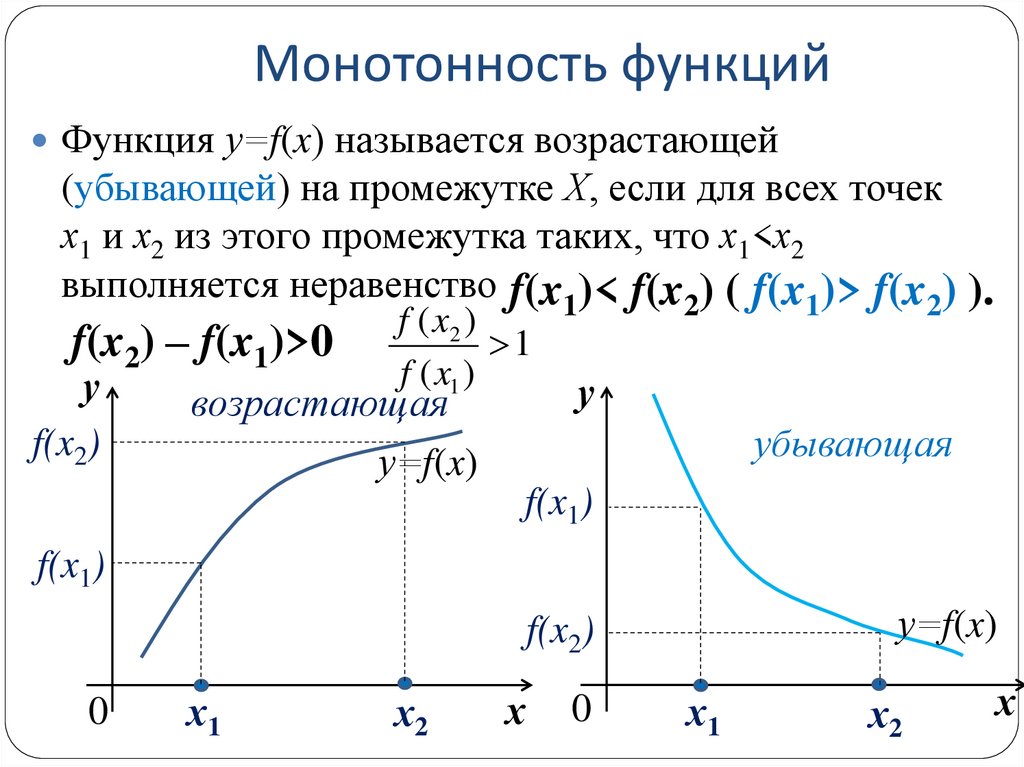
Функция у=f(x) называется возрастающей
(убывающей) на промежутке Х, если для всех точек
х1 и х2 из этого промежутка таких, что х1<х2
выполняется неравенство f(x1)< f(x2) ( f(x1)> f(x2) ).
f(x2) – f(x1)>0
у
f(x2)
f ( x2 )
1
f ( x1 )
возрастающая
у=f(x)
у
убывающая
f(x1)
f(x1)
у=f(x)
f(x2)
0
х1
х2
х
0
х1
х2
х

3. Монотонность функций

у возрастающая
у=f(x)
f(x2)
у
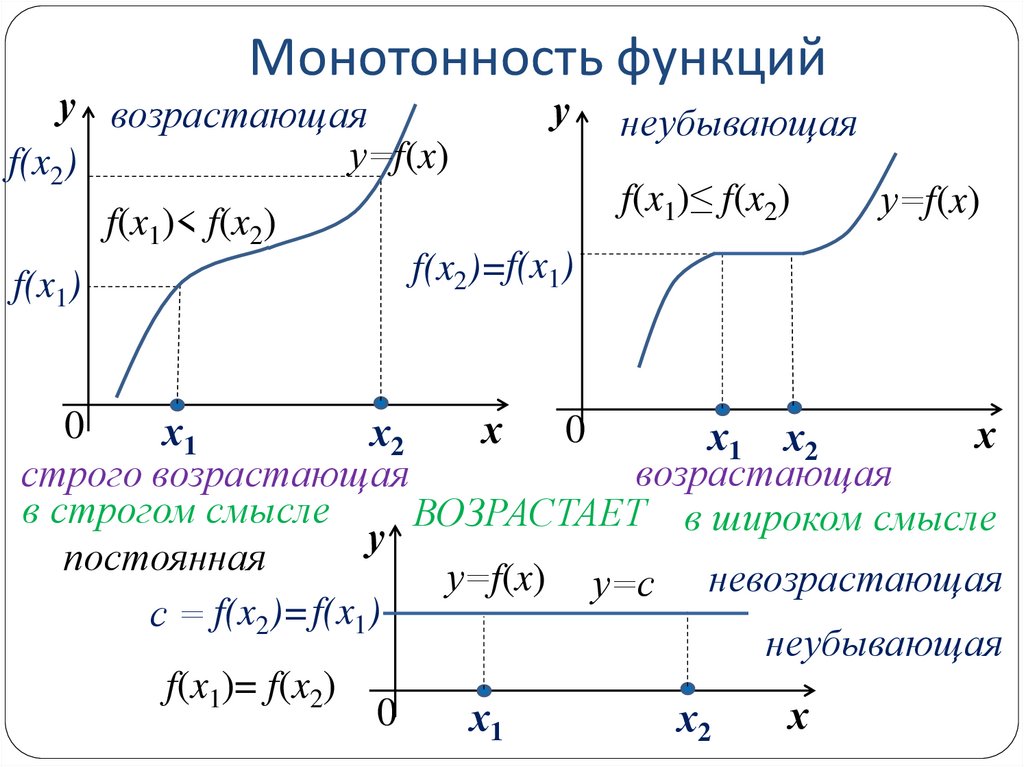
f(x1)< f(x2)
f(x1)
неубывающая
f(x1)≤ f(x2)
у=f(x)
f(x2)=f(x1)
0
0
х
х1
х2
х
х1 х2
возрастающая
строго возрастающая
в строгом смысле
ВОЗРАСТАЕТ в широком смысле
у
постоянная
у=f(x) у=с невозрастающая
с = f(x2)= f(x1)
неубывающая
f(x1)= f(x2)
0
х
х1
х2

4.

Монотонность функций
Функции y=f(x), определенная на множестве Х,
является
x1 , x2 X : x1 x2
возрастающей
убывающей
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
строго монотонные функции
неубывающией
невозрастающей
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
монотонные функции
Интервалы, в которых функция монотонна, называются
интервалами монотонности.

5. Признаки монотонности

Необходимый
Достаточный
Если функция у=f(x)
Если функции f (x)
дифференцируема на
интервале (a; b) и
возрастает (убывает) на
нем, то для всех х из
этого интервала
выполняется
неравенство f /(x) ≥ 0
( f /(x) ≤ 0 ).
дифференцируема на
интервале (a; b) и на
нем f /(x)>0 (f /(x) < 0),
то функция f (x) в этом
интервале возрастает
(убывает).

6. Необходимый признак монотонности

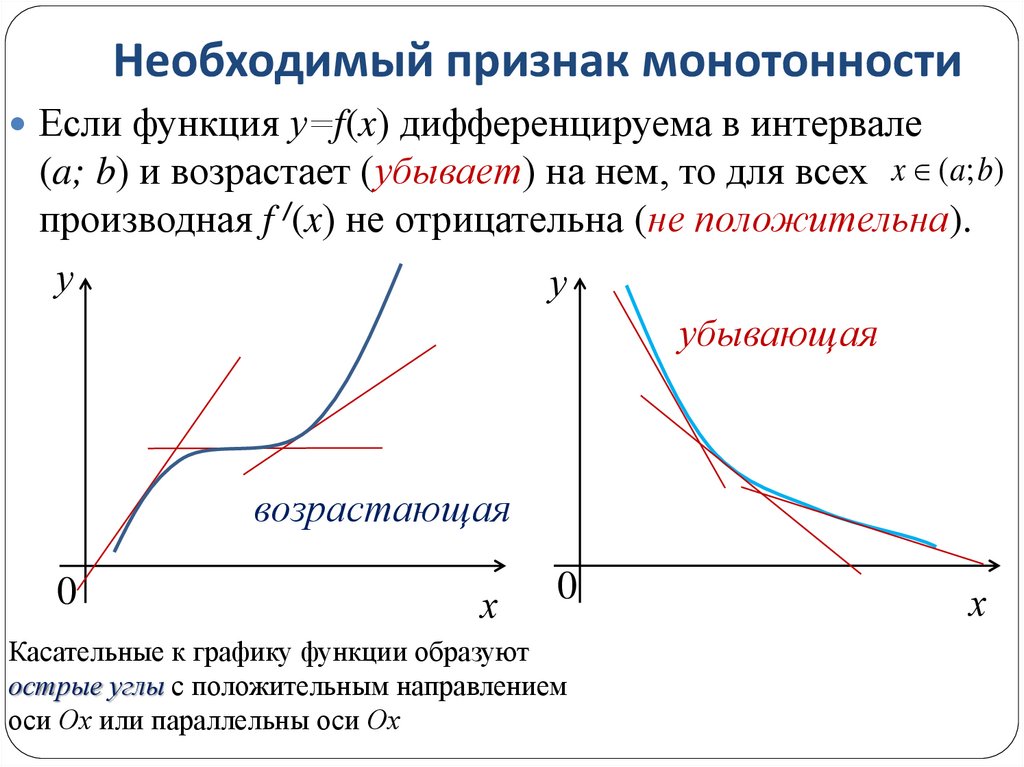
Если функция у=f(x) дифференцируема в интервале
(a; b) и возрастает (убывает) на нем, то для всех x (a; b)
производная f /(x) не отрицательна (не положительна).
у
у
убывающая
возрастающая
0
х
0
Касательные к графику функции образуют
острые углы с положительным направлением
оси Ох или параллельны оси Ох
х

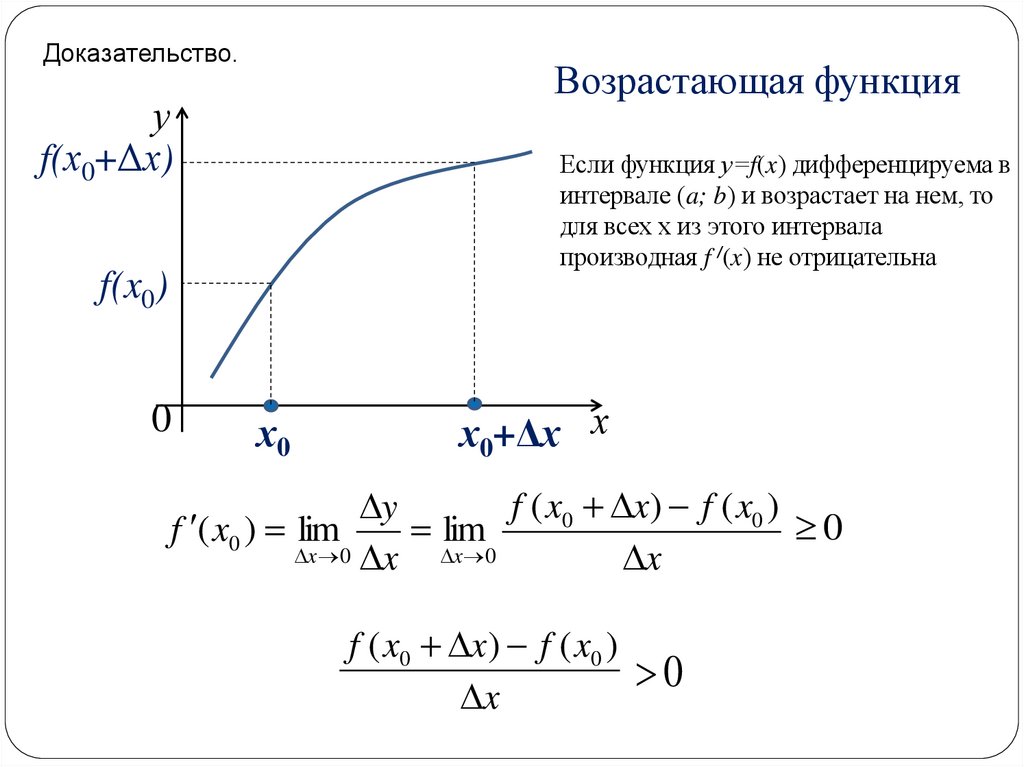
7.

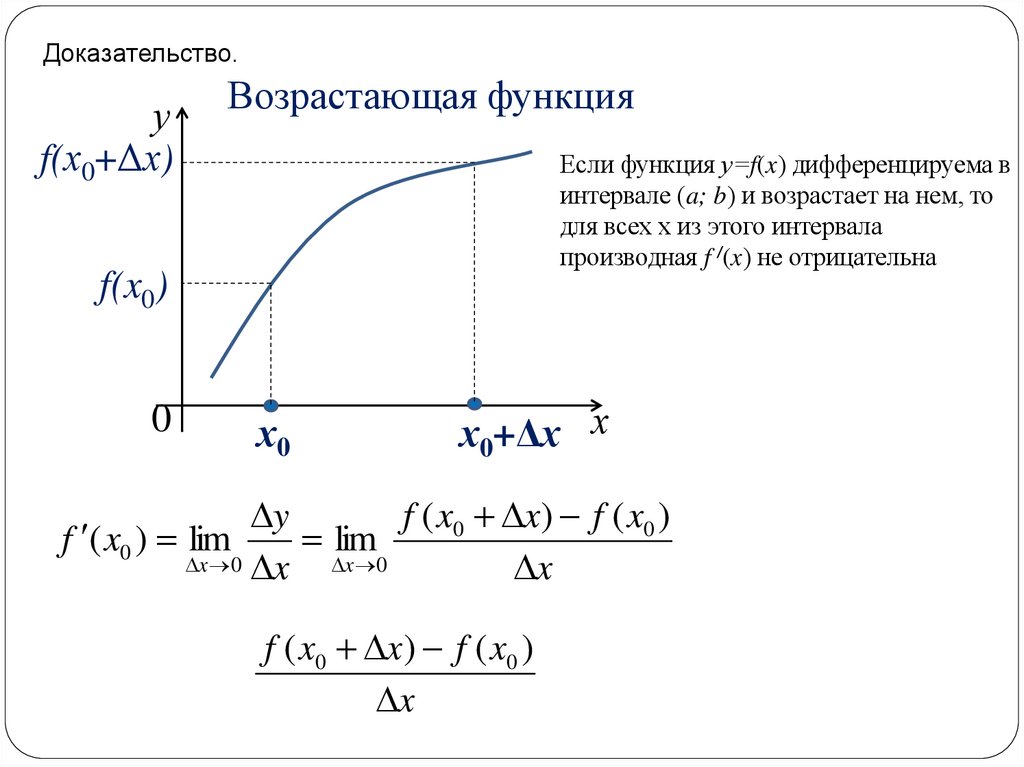
Доказательство.
у
f(х0+Δх)
Возрастающая функция
Если функция у=f(x) дифференцируема в
интервале (a; b) и возрастает на нем, то
для всех х из этого интервала
производная f /(x) не отрицательна
f(x0)
0
х0
х0+Δх х
f ( x0 x) f ( x0 )
y
f ( x0 ) lim
lim
x 0 x
x 0
x
f ( x0 x) f ( x0 )
x

8.

Доказательство.
Возрастающая функция
у
f(х0+Δх)
Если функция у=f(x) дифференцируема в
интервале (a; b) и возрастает на нем, то
для всех х из этого интервала
производная f /(x) не отрицательна
f(x0)
0
х0+Δх х
х0
f ( x0 x) f ( x0 )
y
0
lim
x 0 x
x 0
x
f ( x0 ) lim
f ( x0 x) f ( x0 )
0
x

9. Достаточный признак монотонности

Если функции f (x) дифференцируема на интервале и
производная f /(x) всюду в интервале положительна
(отрицательна), то функция f (x) в этом интервале
возрастает (убывает).
Доказательство.
f ( х) 0 x (a; b) x1 (a; b) x2 (a; b)
x1 x2
f ( x2 ) f ( x1 ) f (c) ( x2 x1 ) 0 с ( x1; x2 )
Формула конечных приращений
(Теорема Лагранжа)
f ( x2 ) f ( x1 )
Функция возрастающая

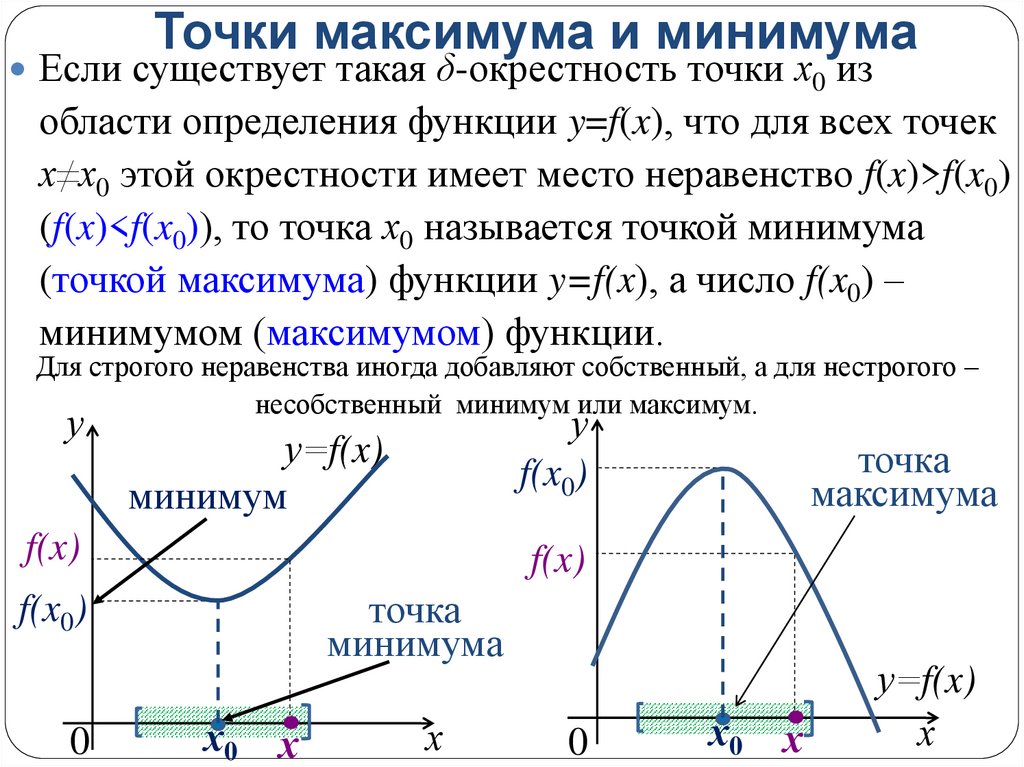
10. Точки максимума и минимума

Если существует такая δ-окрестность точки х0 из
области определения функции y=f(x), что для всех точек
х≠х0 этой окрестности имеет место неравенство f(x)>f(x0)
(f(x)<f(x0)), то точка х0 называется точкой минимума
(точкой максимума) функции y=f(x), а число f(x0) –
минимумом (максимумом) функции.
Для строгого неравенства иногда добавляют собственный, а для нестрогого –
несобственный минимум или максимум.
у
у
f(x0)
у=f(x)
минимум
f(x)
f(x)
точка
минимума
f(x0)
0
точка
максимума
х0
х
х
0
х0
х
у=f(x)
х

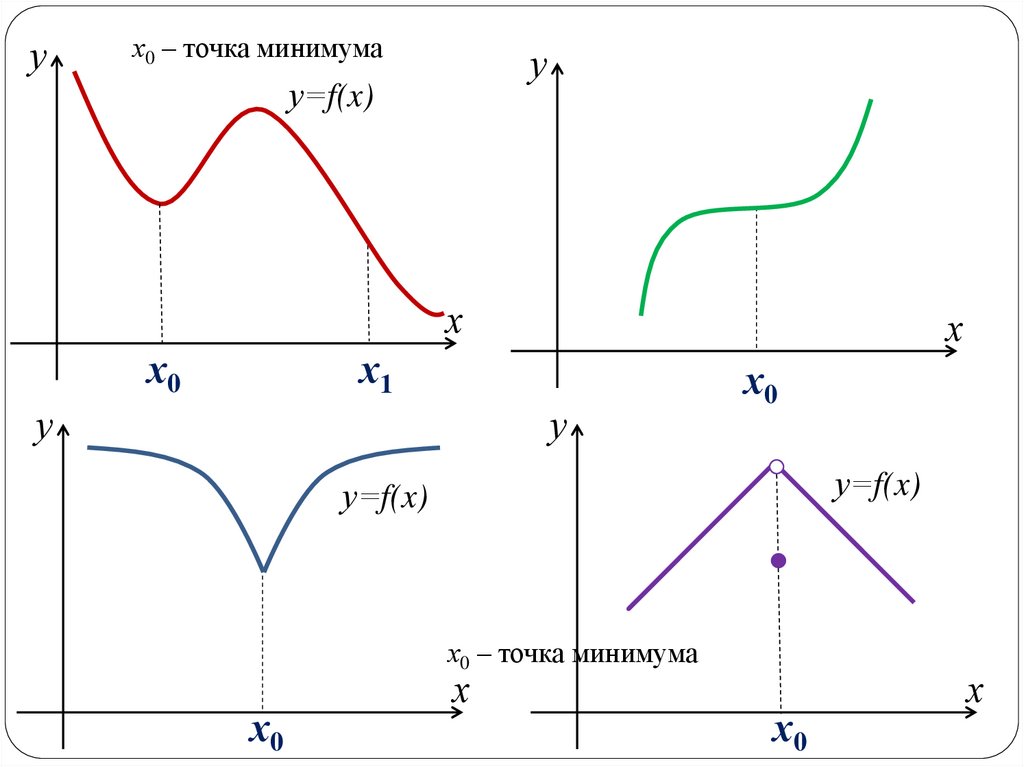
11.

у
х0 – точка минимума
у
у=f(x)
х
х0
х
х1
у
у
х0
у=f(x)
у=f(x)
х0 – точка минимума
х0
х
х0
х

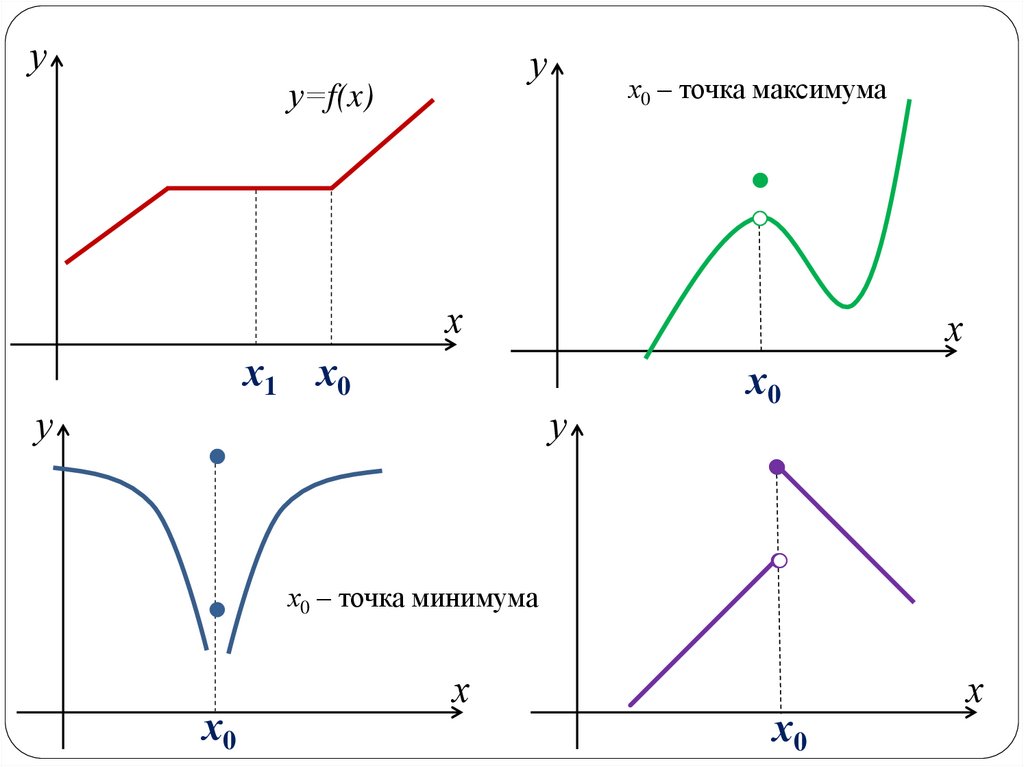
12.

у
у
у=f(x)
х0 – точка максимума
х
х1
х
х0
у
у
х0
х0 – точка минимума
х0
х
х0
х

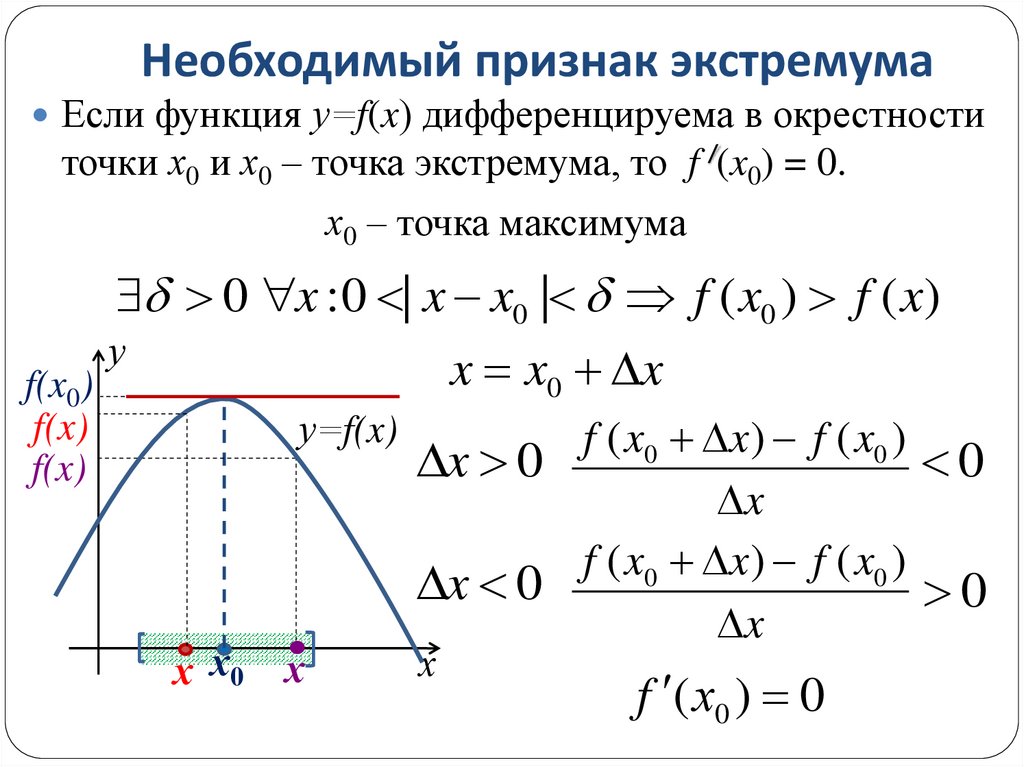
13. Необходимый признак экстремума

Если функция у=f(x) дифференцируема в окрестности
точки х0 и х0 – точка экстремума, то f /(x0) = 0.
х0 – точка максимума
0 x : 0 | x x0 | f ( x0 ) f ( x)
у
x x0 x
f(x0)
у=f(x)
f(x)
f(x)
х х0
х
f ( x0 x) f ( x0 )
x 0
0
x
f ( x0 x) f ( x0 )
x 0
0
x
х
f ( х0 ) 0

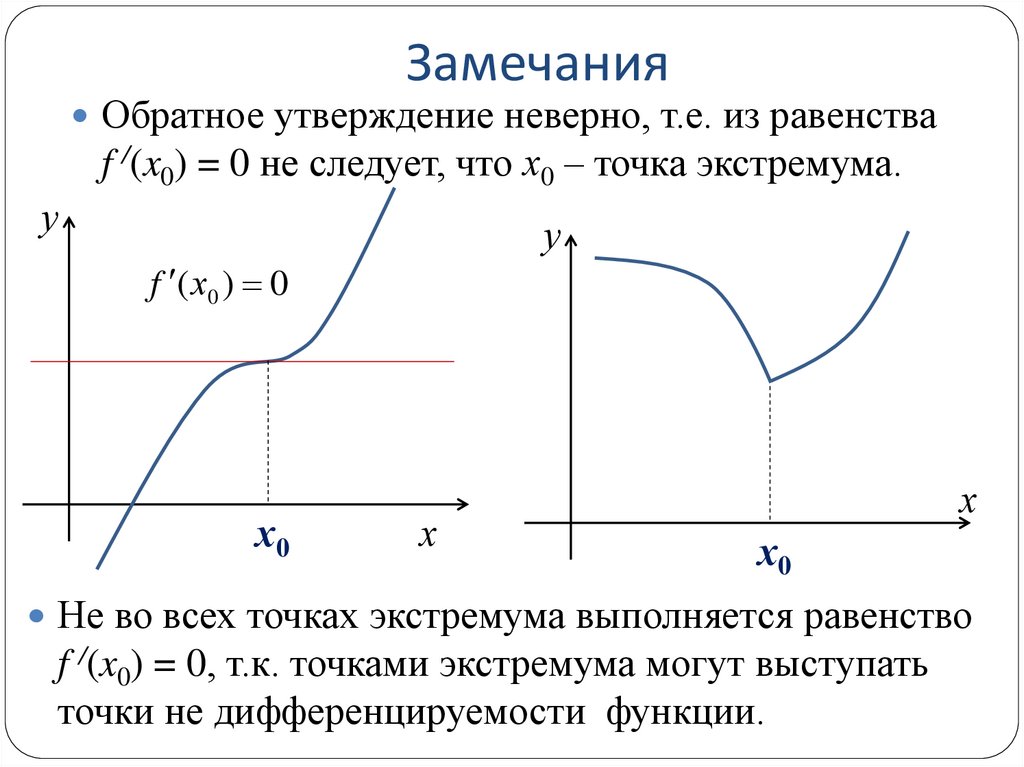
14. Замечания

Обратное утверждение неверно, т.е. из равенства
f /(x0) = 0 не следует, что х0 – точка экстремума.
у
у
f ( х0 ) 0
х0
х
х
х0
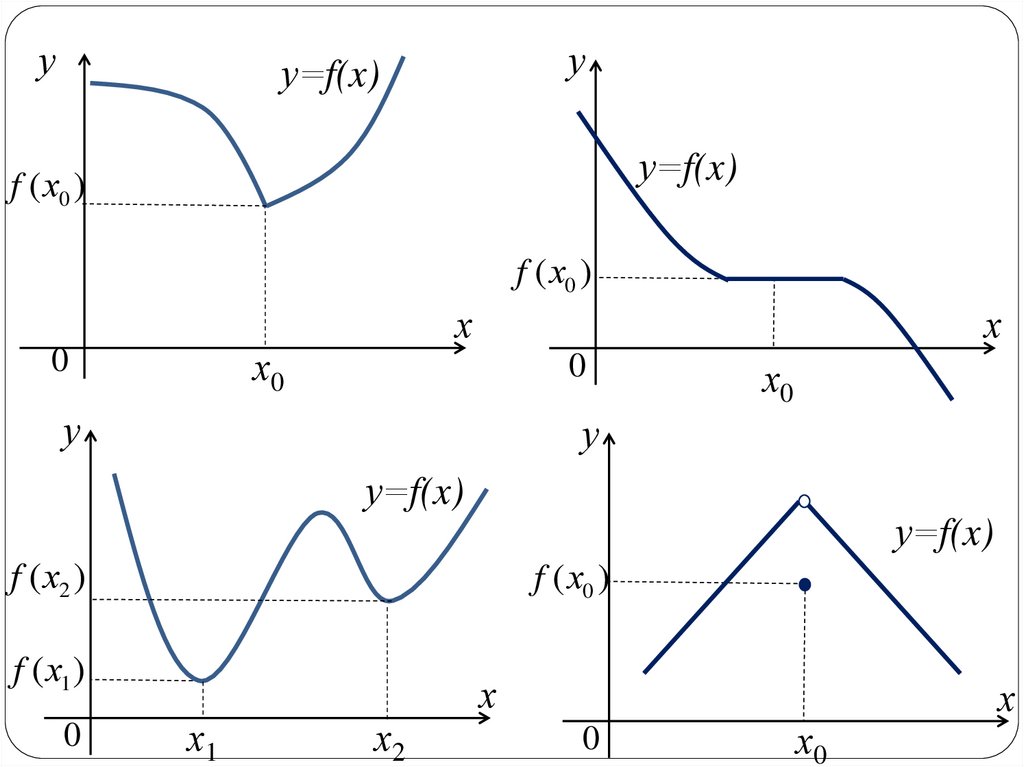
Не во всех точках экстремума выполняется равенство
f /(x0) = 0, т.к. точками экстремума могут выступать
точки не дифференцируемости функции.

15.

у
у
у=f(x)
у=f(x)
f ( х0 )
f ( х0 )
х
х0
0
х
0
у
х0
у
у=f(x)
у=f(x)
f ( х2 )
f ( х0 )
f ( х1 )
0
х1
х2
х
0
х0
х

16. Критические точки

• Точки области определения функции, в которых
производная функции равна нулю, либо равна
бесконечности, либо не существует.
Стационарные точки
Точки, в которых производная равна нулю.
Критические точки
Точки экстремума
Стационарные точки

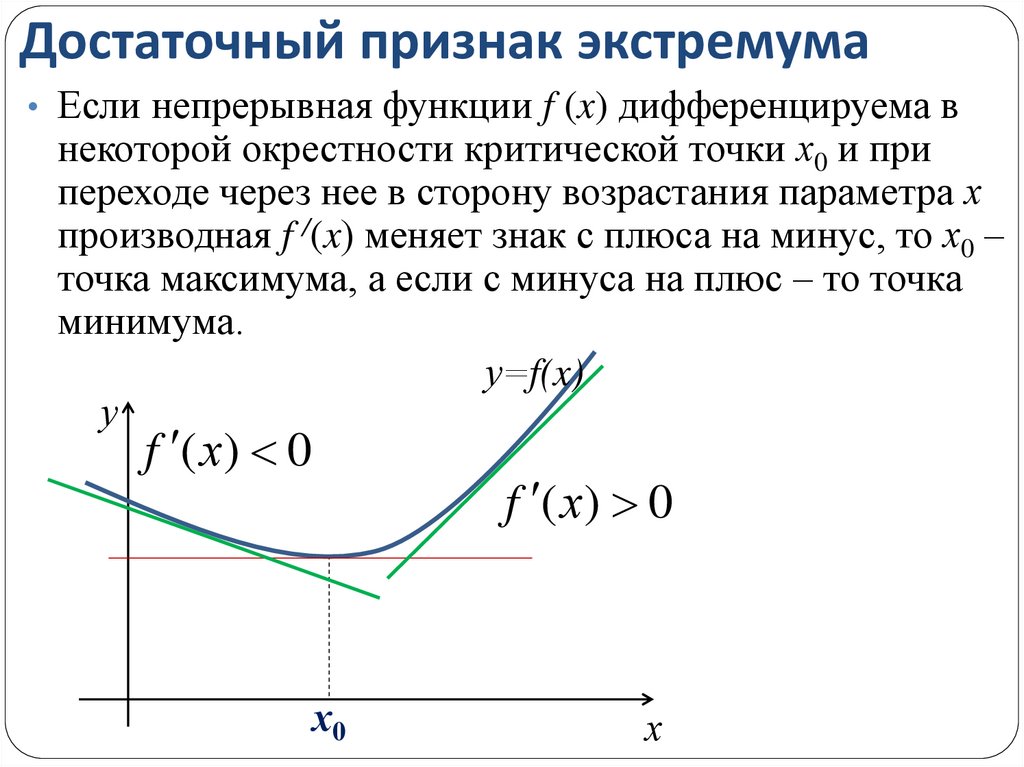
17. Достаточный признак экстремума

• Если непрерывная функции f (x) дифференцируема в
некоторой окрестности критической точки х0 и при
переходе через нее в сторону возрастания параметра х
производная f /(x) меняет знак с плюса на минус, то х0 –
точка максимума, а если с минуса на плюс – то точка
минимума.
у=f(x)
у
f ( х) 0
f ( х) 0
х0
х

18. Достаточный признак экстремума (в терминах второй производной)

• Если функции f (x) дважды дифференцируема в некоторой
окрестности стационарной точки х0 , в которой
производная второго порядка существует и отлична от
нуля (f //(x0) ≠ 0), то при условии f //(x0) < 0 в точке х0
функция f (x) имеет максимум,
а при f //(x0) > 0 в точке х0 – минимум.
f ( x0 x) f ( x0 )
f ( x0 x)
f ( x0 ) lim
lim
0
x 0
x 0
x
x

19. Экстремумы функции

• Точки максимума и минимума называют точками
экстремума, а максимум или минимум функции
называют её экстремумом.
• Точки максимума и минимума – экстремальные точки
функции.
• Точки максимума (минимума) обозначаются хmax (xmin);
а максимум (минимум) – уmax (уmin) или fmax (fmin).
• Латинские extremum означает «крайнее», maximum –
«наибольшее», minimum – «наименьшее» (значение).
Не путайте экстремумы функции с наибольшим и
наименьшим значением функции.

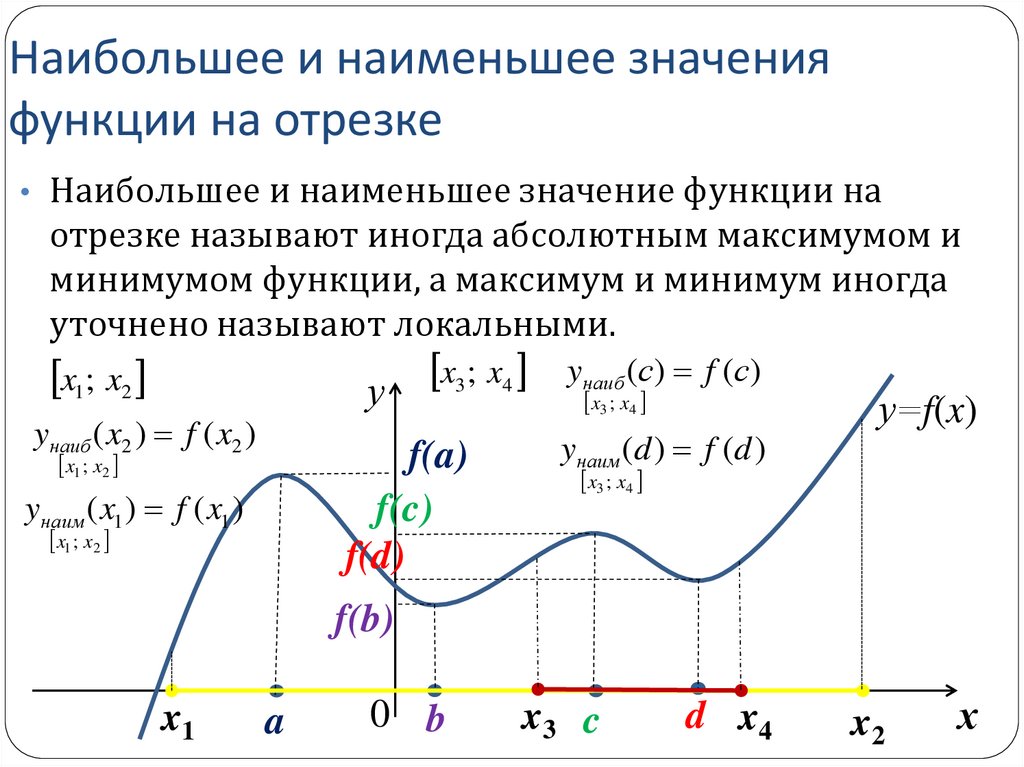
20. Наибольшее и наименьшее значения функции на отрезке

• Наибольшее и наименьшее значение функции на
отрезке называют иногда абсолютным максимумом и
минимумом функции, а максимум и минимум иногда
уточнено называют локальными.
x1; x2
у
yнаиб ( x2 ) f ( x2 )
x3 ; x4
f(a)
f(c)
f(d)
x1 ; x2
yнаим ( x1 ) f ( x1 )
x1 ; x2
yнаиб (с) f (с)
x3 ; x4
yнаим (d ) f (d )
у=f(x)
x3 ; x4
f(b)
x1
a
0 b
x3 c
d x4
x2
х