Прогнозирование экономических показателей с помощью математических моделей

1.

Прогнозирование
экономических показателей с
помощью математических
моделей
Выпускная квалификационная работа бакалавра студента 4 курса очного отделения
Магомедова Нажмудина Исламовича по направлению 01.03.02 - Прикладная
математика и информатика.
Научный руководитель: д.ф.-м.н., профессор Кадиев Р.И.
Махачкала, 2025

2.

Актуальность исследования
Экономическая
динамика
Принятие решений
Оптимизация
В условиях постоянно
Математические модели
способствует оптимизации
меняющейся
позволяют выявлять
ресурсов, минимизации
экономической среды,
скрытые закономерности,
рисков и повышению
точное прогнозирование
оценивать влияние
эффективности управления
экономических
различных факторов и
в различных секторах
показателей становится
предсказывать будущие
экономики.
критически важным для
тенденции, что
принятия обоснованных
незаменимо для
решений на всех уровнях.
стратегического
Применение моделей
планирования.

3.

Содержание работы
Введение
Обзор актуальности и целей исследования.
Глава 1: Математические модели временных рядов и их построение
Определение, классификация и особенности временных рядов, а также базовые модели и этапы их построения.
Глава 2: Регрессионные математические модели и их построение
Основы регрессионного анализа, виды моделей и методы оценки параметров.
Глава 3: Применение математических моделей для построения прогнозов
Практическое применение временных рядов и регрессионных моделей для прогнозирования экономических показателей.
Заключение
Основные выводы и результаты работы.
Список использованных источников
Перечень литературы и ресурсов.

4.

Математические модели временных рядов
Определение и классификация
Временной ряд – это хронологическая последовательность наблюдений за показателем {yt}, t = 1, ..., n. Они
классифицируются по способу измерения времени (моментные, интервальные), частоте наблюдений (высоко-,
средне-, низкочастотные) и стационарности (стационарные, нестационарные).
Структурные компоненты включают тренд, сезонность, цикличность и случайную компоненту. Особенности:
взаимозависимость наблюдений, структурная неоднородность, пропущенные данные, выбросы и многомерность.
Базовые модели временных рядов включают авторегрессионные модели (AR), модели скользящего среднего (MA) и их комбинации (ARMA, ARIMA, SARIMA). Также используются векторная авторегрессия (VAR) и методы
экспоненциального сглаживания (SES, Holt, Holt-Winters).
Авторегрессионная модель AR(p):
Модель скользящего среднего MA(q):

5.

Этапы построения моделей временных рядов
Сбор и подготовка данных
Упорядочивание данных по времени, заполнение пропущенных значений, удаление выбросов.
Первичный анализ данных
Визуальный анализ графиков, анализ автокорреляционной функции (ACF) и частной автокорреляционной функции (PACF).
Проверка стационарности
Использование тестов Дики-Фуллера (ADF) и KPSS; дифференцирование при необходимости.
Выбор и оценка модели
Выбор AR, MA, ARMA, ARIMA, SARIMA или VAR в зависимости от характеристик ряда. Оценка параметров методом максимального правдоподобия или наименьших квадратов.
Диагностика и валидация
Проверка остатков на автокорреляцию (тест Льюнга-Бокса), гетероскедастичность (тест Бройша-Пагана). Валидация на отложенной выборке.
Прогнозирование и интерпретация
Использование модели для прогнозирования будущих значений и интерпретация результатов для принятия решений.

6.

Регрессионные математические
модели
Основы регрессионного анализа
Модель парной линейной
регрессии
Регрессионный анализ исследует
Простейший случай, связывающий две
стохастические взаимосвязи между
переменные:
переменными, строя математическую модель
зависимости результативного признака Y от
факторов X₁, X₂, ..., Xk. Цели: установление
формы зависимости, количественная оценка
влияния факторов, прогнозирование и
выявление закономерностей.
где Y – объясняемая переменная, X –
независимая, β₀ и β₁ – параметры, ε –
случайная ошибка.
Модель множественной линейной регрессии
Объясняемая переменная зависит от нескольких предикторов:
Коэффициенты β показывают изменение Y при изменении соответствующего Xᵢ на единицу, при
прочих равных условиях.

7.

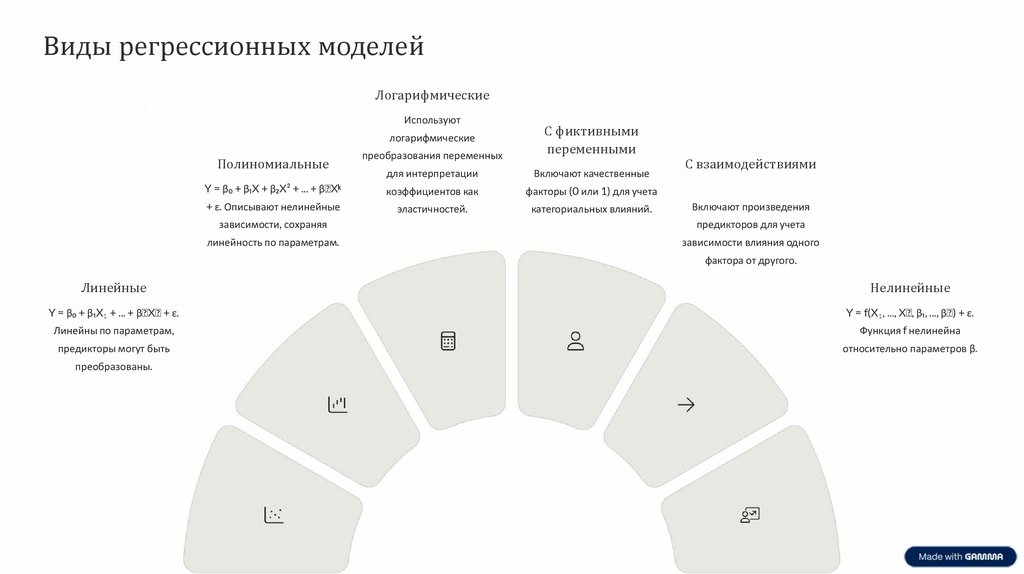
Виды регрессионных моделей
Логарифмические
Используют
Полиномиальные
преобразования переменных
С фиктивными
переменными
для интерпретации
Включают качественные
Y = β₀ + β₁X + β₂X² + ... + βₖXᵏ
коэффициентов как
факторы (0 или 1) для учета
+ ε. Описывают нелинейные
эластичностей.
категориальных влияний.
логарифмические
С взаимодействиями
Включают произведения
зависимости, сохраняя
предикторов для учета
линейность по параметрам.
зависимости влияния одного
фактора от другого.
Линейные
Нелинейные
Y = β₀ + β₁X₁ + ... + βₖXₖ + ε.
Y = f(X₁, ..., Xₖ, β₁, ..., βₖ) + ε.
Линейны по параметрам,
Функция f нелинейна
предикторы могут быть
относительно параметров β.
преобразованы.

8.

Применение временных рядов
для прогнозирования
Загрузка и визуализация данных
Использование ежемесячной статистики объема розничных продаж в России
(2015-2025).
Проверка стационарности
Применение теста Дики-Фуллера и дифференцирование при необходимости.
Построение и оценка модели ARIMA
Разделение на обучающую и тестовую выборки, построение модели
ARIMA(1,1,1) и оценка качества с помощью MAE и RMSE.
Прогнозирование
Построение прогноза на следующие 6 месяцев с расчетом 95%
доверительных интервалов.

9.

Применение регрессионных
моделей для прогнозирования
Генерация и анализ данных
Создание синтетических экономических данных (ИПЦ, безработица, денежная масса,
обменный курс, процентная ставка) и анализ корреляций.
Построение и оценка моделей
Использование линейной регрессии, Ridge, Lasso, Random Forest, Gradient Boosting.
Сравнение моделей по MAE, RMSE, R².
Анализ важности признаков
Оценка влияния каждого экономического фактора на ИПЦ для выбранных моделей.
Построение прогноза
Прогнозирование ИПЦ на будущие периоды с использованием лучшей модели.