Similar presentations:
Модели статистического прогнозирования
1. Модели статистического прогнозирования
0011 0010 1010 1101 0001 0100 10111
2
4
Д/з: § 18 (вопросы
и задания)
2.
Рассмотрим способ нахождения зависимости частоты заболеваемостижителей города бронхиальной астмой от качества воздуха.
0011 0010 1010 1101 0001 0100 1011
Качество воздуха
в городе(чем хуже воздух, тем больше
больных астмой)
Определим
характер
зависимости
1
Частота легочных
заболеваний
Качественное
заключение. Его не
достаточно для того
чтобы управлять уровнем
загрязнённости воздуха
2
4
Нужно установить, какие именно примеси сильнее
всего влияют на здоровье людей, как связана
концентрация этих примесей в воздухе с числом
заболеваний. Такую зависимость можно
установить только экспериментальным путём:
посредством сбора многочисленных данных, их
анализа и обобщения.
3. Статистика - наука о сборе, измерении и анализе массовых количественных данных
Статистика - наука о сборе, измерениии анализе массовых количественных
0011 0010 1010 1101 0001 0100 1011
данных
Виды статистики:
• медицинская статистика
• математический аппарат статистики разрабатывает наука
под названием математическая статистика
• экономическая статистика
• социальная статистика …
1
2
4
Зависимости устанавливаются экспериментальным путем:
-сбор данных;
- анализ;
- обобщение.
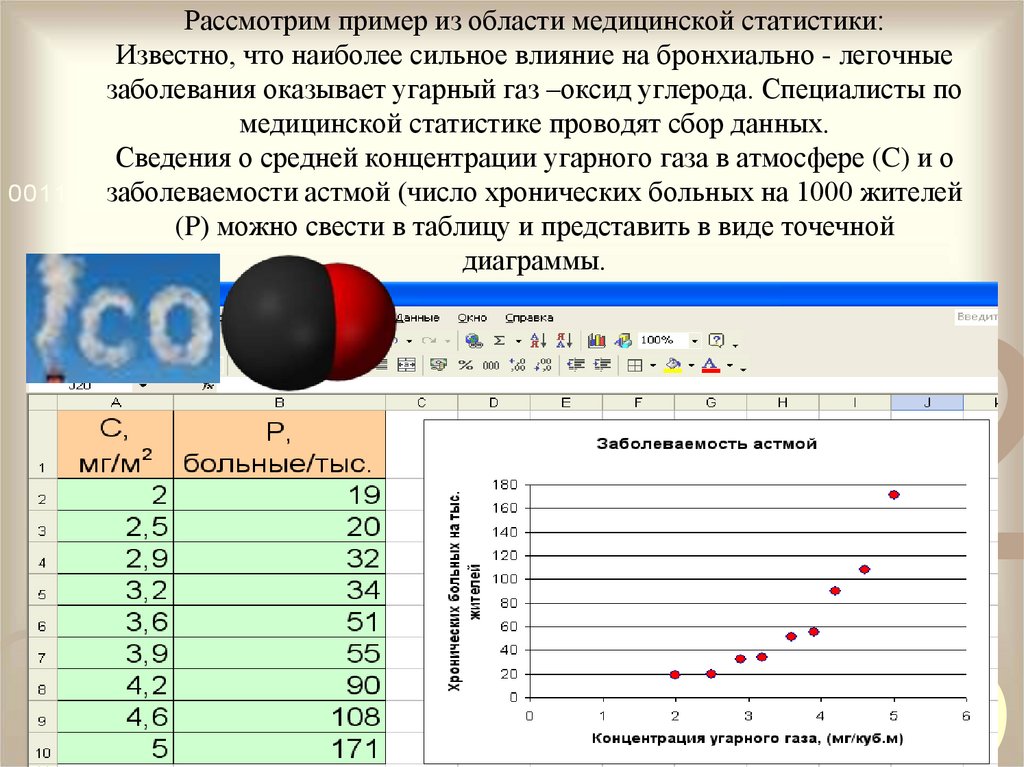
4. Рассмотрим пример из области медицинской статистики: Известно, что наиболее сильное влияние на бронхиально - легочные
заболевания оказывает угарный газ –оксид углерода. Специалисты помедицинской статистике проводят сбор данных.
Сведения о средней концентрации угарного газа в атмосфере (C) и о
заболеваемости
астмой
(число
0011 0010
1010 1101 0001
0100
1011 хронических больных на 1000 жителей
(P) можно свести в таблицу и представить в виде точечной
диаграммы.
1
2
4
5. 2 варианта построения графической зависимости по экспериментальным данным
0011 0010 1010 1101 0001 0100 10111
2
4
Основные требования к искомой функции:
- она должна быть достаточно простой для использования ее в дальнейших
вычислениях;
-график функции должен проходить вблизи экспериментальных точек так, чтобы
отклонения этих точек о графика были минимальны и равномерны.
Полученную таким образом функцию называют в статистике регрессионной
моделью.
6. Получение регрессивной модели происходит в два этапа:
1) подбор вида функции:y = ax + b - линейная функция;
0011 0010 1010
1101 0001 0100 1011
y = ax2 + bx
+ c - квадратичная функция (полиномиальная);
y=a ln(x) +b - логарифмическая функция;
y = aebx- экспоненциальная функция;
y = axb - степенная функция.
Во всех этих формулах х -аргумент, у- значение функции, a,b,c,dпараметры функции, ln(x) –натуральный логарифм, e –константа,
основание логарифма.
2) вычисление параметров функции:
1
2
4
метод наименьших квадратов (МНК) - сумма квадратов отклонений y-
координат всех экспериментальных точек от y-координат графика функции
должна быть минимальной.
7.
Метод наименьших квадратов (МНК) был предложен вXVIII веке немецким учёным математиком К.Гауссом.
0011 0010 1010 1101 0001 0100 1011
1
2
4
8. Метод наименьших квадратов
y=ax+b – линейная функция;0011
0010 1010 1101 0001 0100 1011
y=ax2+bx+c – квадратичная функция;
y=a ln(x)+b – логарифмическая функция;
y=aebx – экспоненциальная функция;
y=axb – степенная функция;
y=ax3+bx2+cx+d – полином 3 степени.
y=46,361x-99,881
R2=0,8384
График
регрессионной
модели
называется
ТРЕНДОМ
(англ. “trend”) –
общее
направление
или тенденция
y=3.4302e0,7555x
R2=0,9716
1
2
4
y=21,845x2-106,97x+150,21
R2=0,9788
9. Графики функций, построенные по МНК, - тренды
0011 0010 1010 1101 0001 0100 10111
2
4
Обратим внимание на подписи, присутствующие на графиках.
Во-первых, это записанные в явном виде искомые функции –регрессионные модели.
На графиках присутствует ещё одна величина, полученная в результате построения
трендов. Она обозначена как R2. В статистике эта величина называется
Коэффициентом детерминированности, который всегда заключён в диапазоне
от 0 до 1.
10.
Коэффициент детерминированности2 – коэффициент детерминированности
R
0011 0010 1010 1101 0001 0100 1011
(определяет, насколько удачной является
полученная регрессионная модель). Если он равен
1, то функция точно проходит через табличные
значения, если 0, то выбранный вид регрессионной
модели предельно неудачен.
Чем R2 ближе к 1, тем удачнее
регрессионная модель.
1
2
4
11. Алгоритм построения регрессионной модели по МНК с помощью MS Excel (линейный тренд)
• Ввеститабличные
данные
зависимости
0011 0010
1010 1101
0001 0100
1011
заболеваемости P от
концентрации угарного газа С .
Построить точечную диаграмму.
Выполнить команду: Макет – Линия тренда;
В открывшемся окне на вкладке Тип выбрать Линейный тренд;
Перейти на вкладку Параметры и установить галочки на
флажках показывать уравнения на диаграмме и поместить на
диаграмме величину достоверности аппроксимации R^2
• щелкнуть OK.
1
2
4
12. Практическая работа 3.1 Получение регрессионных моделей в MS Excel
0011 0010 1010 1101 0001 0100 1011Цель работы: освоение способов построения по
экспериментальным данным регрессионной
модели и графического тренда средствами
табличного процессора MS Excel.
1
2
4
Семакин И.Г. Практикум. Информатика и ИКТ 11 кл., стр.209
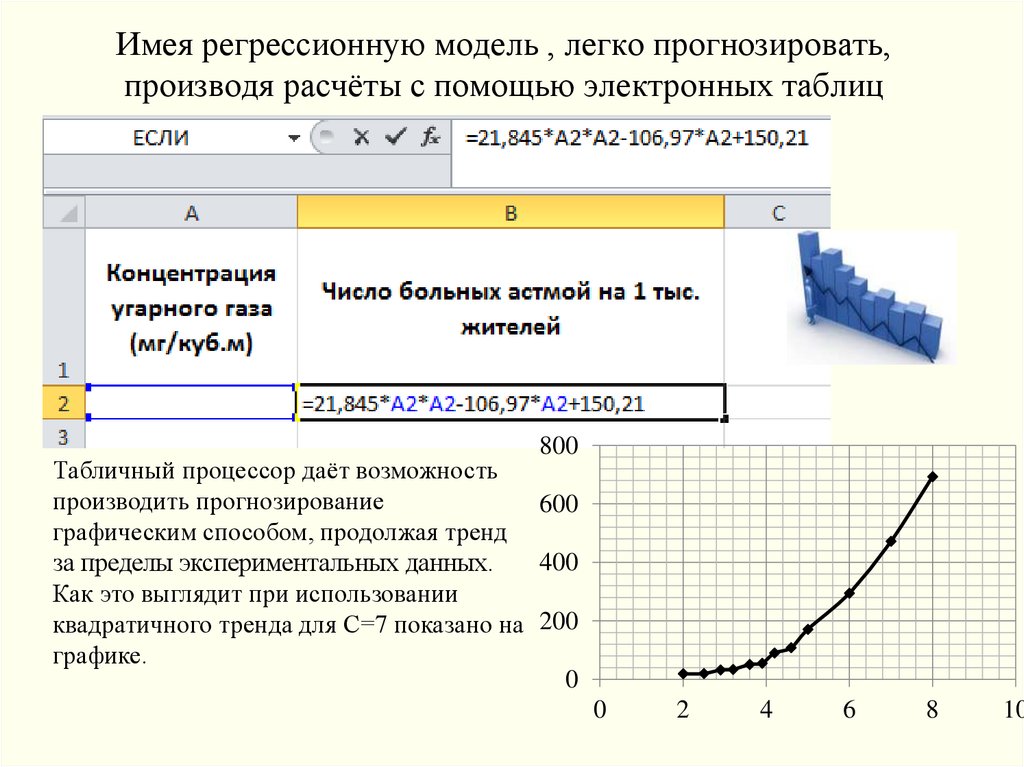
13. Имея регрессионную модель , легко прогнозировать, производя расчёты с помощью электронных таблиц
800Табличный процессор даёт возможность
производить прогнозирование
600
графическим способом, продолжая тренд
400
за пределы экспериментальных данных.
Как это выглядит при использовании
квадратичного тренда для С=7 показано на 200
графике.
0
0
2
4
6
8
10
14. ПРОГНОЗИРОВАНИЕ ПО РЕГРЕССИОННОЙ МОДЕЛИ Существует два способа прогнозирования по регрессионной модели:
2 190011 0010 1010 1101 0001 0100 1011
2,5
2,9
3,2
3,6
3,9
4,2
4,6
5
6
7
8
20
32
34
51
55
90
108
171
295
472
693
Восстановление значений – прогноз в
пределах экспериментальных значений
независимой переменной.
1
2
4
Экстраполяция – прогнозирование за
пределами экспериментальных данных
15. Ограничения при экстраполяции !
Применимость всякой регрессионной моделиограничена,
особенно
за
пределами
экспериментальной области т.к. экстраполяция
строится на гипотезе.
0011 0010 1010 1101 0001 0100 1011
1
2
4
Вывод: применять экстраполяцию можно только
в областях данных,
близких к
экспериментальной.
16. Практическая работа 3.2 Прогнозирование в MS Excel
0011 0010 1010 1101 0001 0100 1011Цель работы: освоение приемов прогнозирования
количественных характеристик системы по
регрессионной модели путем восстановления значений
и экстраполяции
1
Семакин И.Г. Практикум. Информатика и ИКТ 11 кл., стр.211
2
4
17.
1.По данным из следующей таблицы постройтес помощью Excel линейную, квадратичную,
экспонециальную и логарифмическую
регрессионные модели. Определите
параметры, выберите лучшую модель.
x
2
4
6
8
10
12
14
16
18
20
22
24
26
28
y
44
32
35
40
30
27
21
25
20
23
18
19
20
16
2.Соберите данные о средней дневной
температуре в вашем городе за последнюю
неделю. Оцените, годиться ли использование
линейного тренда для описания характера
изменения температуры. Попробуйте путем
графической экстраполяции предсказать
температуру через 2-5 дней.
18.
0011 0010 1010 1101 0001 0100 10111
2
4















 mathematics
mathematics








