Similar presentations:
Кинематика движения материальной точки. Тема 1
1. Тема 1. КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ппп
12.
1.1. Понятие механики, разделы вмеханике
Механика - часть физики, которая изучает
закономерности механического движения и причины,
вызывающие или изменяющие это движение.
Механическое движение - изменение взаимного
положения тел или их частей в пространстве со
временем.
Механика
Классическая
(механика ГалилеяНьютона)
Изучает законы движения
макроскопических тел,
скорости которых малы
по сравнению со скоростью
света в вакууме с.
v/c <<1
Релятивистская –
Квантовая –
изучает законы движения
макроскопических тел со
скоростями, сравнимыми с с.
Основана на СТО.
Изучает законы движения
микроскопических тел
(отдельных атомов и
элементарных частиц)
3.
Предметомклассической
механики
является
механическое движение взаимодействующих между
собой макротел при скоростях, много меньше
скорости света и в условиях, когда переходом
механической энергии в другие ее формы можно
пренебречь.
Разделы
классической механики
Кинематика
Динамика
Изучает движение тел,
не рассматривая причины,
которые это движение
обусловливают
Изучает законы движения тел
и причины,
которые вызывают или
изменяют это движение
Статика
Изучает законы равновесия
системы тел.
Если известны законы движения тел,
то из них можно установить и
законы равновесия.
4.
Кинематика (от греческого словаkinema – движение) – раздел механики, в
котором изучаются геометрические
свойства движения тел без учета их
массы и действующих на них сил.
Динамика (от греческого dynamis –
сила) изучает движения тел в связи с теми
причинами, которые обуславливают это
движение.
Статика (от греческого statike –
равновесие) изучает условия равновесия тел.
4
5. Модели в механике
Материальная - тело, размерами, формой иточка
внутренним строением которого в
данной задаче можно пренебречь
Абсолютно твердое - тело, которое ни при каких
тело
условиях не может деформироваться
и при всех условиях расстояние
между двумя точками этого тела
остается постоянным
Абсолютно упругое - Тело, деформация которого
тело
подчиняется закону Гука, а после
прекращения действия внешних
сил принимает свои
первоначальные размеры и форму.
6. 1.2. Система отсчета, тело отсчета
Всякое движение относительно,поэтому
для
описания
движения
необходимо условиться,
относительно
какого другого тела будет отсчитываться
перемещение данного тела. Выбранное
для этой цели тело называют телом
отсчета.
Практически, для описания движения
приходится связывать с телом отсчета
систему
координат
(декартова,
сферическая, цилиндрическая и т.д.).
6
7.
Системаотсчета
–
совокупность системы координат и
часов, связанных с телом по
отношению к которому изучается
движение.
Движения тела, как и материи, вообще
не
может
быть
вне
времени
и
пространства. Материя, пространство и
время неразрывно связаны между собой
(нет пространства без материи и времени и
наоборот).
7
8.
Пространство трехмерно,поэтому
«естественной»
системой координат является,
декартова или прямоугольная
система координат, которой мы в
основном и будем пользоваться.
В
декартовой
системе
координат, положение точки А в
данный момент времени по
отношению к этой системе
характеризуется
тремя
координатами x, y, z или радиусвектором
проведенным
из
начала
координат в данную
точку
r
8
9.
Рисунок 2.1При движении материальной точки её
координаты
с
течением
времени
изменяются.
В общем случае её движение
определяется
скалярными
или
9
векторными уравнениями:
10.
Кинематические уравнения движенияматериальной точки:
x x(t ),
y y (t ),
z z (t ).
r x i y j zk
Эти уравнения эквивалентны векторному уравнению
где х, у, z – проекции радиус-вектора r на
оси координат, а i, j, k – единичные
векторы (орты), направленные по
соответствующим осям, причем
k i , j , i j , k , j k, i
10
10
11.
Числонезависимых
координат,
полностью
определяющих
положение
точки
в
пространстве,
называется
числом степеней свободы i
Если материальная точка движется в
пространстве, то она имеет три степени
свободы i=3 (координаты х, у, z). Если она
движется на плоскости – две степени
свободы i=2. Если вдоль линии – одна
степень свободы i=1.
11
12. 1.3. Кинематика материальной точки
1.3.1. Путь, перемещениеПоложение точки А в пространстве
можно задать с помощью радиус-вектора r1
проведенного из точки отсчета О или начала
координат
12
13.
При движении точки А из точки 1 в точку 2 её радиусвекторизменяется и по величине, и по направлению,
т.е. r зависит от времени t.
Геометрическое
место точек
концов r называется траекторией точки.
Длина траектории есть путь Δs. Если
точка движется по прямой, то приращение r
13
равно пути s.
14.
Пусть за время t точкапереместилась из точки 1 в точку 2.
r
Вектор перемещения
приращение r1
за время t
r r2 r1 x x0 i y y0 j z z0 k;
Δ r Δx i Δy j Δzk
А
есть
(1.3.1)
(1.3.2)
Модуль вектора:
Δ r Δx Δy Δz .
2
2
2
14
(1.3.3)
15.
1.3.2. Скорость15
16. Скорость
Среднийвектор
скорости
определяется как отношение вектора
перемещения r ко времени t, за
которое это перемещение произошло
Δr
Δt
Вектор r
совпадает с
направлением
вектора υ
16
17.
Мгновенная скорость в точке 1:Δr dr
lim .
Δt dt
Δt 0
Модуль вектора скорости
dr
.
dt
Мгновенная скорость -вектор скорости
в данный момент
времени
равен
первой
производной от r по времени и направлен
по касательной к траектории в данной
17
точке в сторону движения точки А.
18.
При t 0 т.е. набесконечно малом
участке траектории
S = r (перемещение
совпадает с траекторией)
В этом случае
мгновенную скорость
можно выразить через
скалярную величину –
путь:
Δs ds
υ lim
;
Δt 0
Δt dt
ds
или υ
.
dt
Так вычислять скорость проще, т.к. S – скаляр
18
19.
Так какТогда
dr
dt
2
i
n
...
1
.
n
i 1
i
Таким
образом,
скорость
тоже
подчиняется
принципу
независимости
движения.
В дальнейшем мы подробнее рассмотрим
принцип независимости действия сил.
19
20.
В физике существует общий принцип,который называется
принцип суперпозиции
результирующий эффект сложного
процесса взаимодействия представляет собой сумму эффектов, вызываемых
каждым воздействием в отдельности,
при условии, что последние взаимно не
влияют друг на друга.
Принцип суперпозиции играет большую
роль во многих разделах физики и техники.
20
21. 1.3.3. Проекция вектора скорости на оси координат
В векторной форме уравнения записываютсялегко и кратко. Но для практических вычислений
нужно знать проекции вектора на оси координат
выбранной системы отсчета.
Положение точки А
задается
радиус-вектором r .
Спроецируем вектор r
на оси – x, y, z.
21
22.
Понятно, что х, y, z зависят от времени t,т.е. x(t), y(t), z(t). Зная зависимость этих
координат от времени (закон движения
точки) можно найти в каждый момент
времени скорость точки.
Проекция
скорости
равна:
вектора
на ось x
dx
dt
x
22
23.
Проекции вектора скорости на оси равны:dx
υx
dt
dy
υy
dt
dz
υz .
dt
23
24.
Так как вектор, то(1.3.6)
dx dy dz
υ υx i υ y j υz k i j k,
dt
dt
dt
где i, j, k единичные векторы – орты.
υ x i y j z k
Модуль вектора скорости:
2
2
x
y
2
z
24
25. 1.3.4. Ускорение. Нормальное и тангенциальное ускорения
В произвольном случае движения скорость неостается постоянной. Быстрота изменения
скорости по величине и направлению
характеризуются ускорением:
d
a
dt
Ускорение величина векторная.
(1.3.7)
При криволинейном движении изменяется и по времени
и по направлению. В какую сторону? С какой скоростью?
25
Из выражения (2.3.7) на эти вопросы не ответишь.
26.
Найдем общее ускорение (как производную):dτ
d d
a
τ a a .
dt dt
dt
n
(1.3.8)
Получили два слагаемых ускорения:
a – тангенциальное ускорение,
совпадающее
с направлени
ем
в данной точке.
a – нормальное
n
ускорение или
центростремительное.
26
27.
2728.
При произвольном движенииan
Z
точки имеем:
a
n
a (t ) a an
М
K
O
τ
L
aτ
v
r(t)
Y
X
28
29.
da
τ
dt
или по модулю
τ
dυ
aτ
dt
a τ -показывает изменение вектора скорости
по величине:
d
0
- если
то a направлено
в ту же сторону, что и
dt
вектор т.е. ускоренное движение;
d
- если
0
dt
d
0
- при
dt
то a направлено
в противоположную
сторону , т.е. замедленное движение;
то aτ 0, const – движение
постоянной по модулю скоростью.
29
30.
Рассмотрим подробнее второе слагаемоеуравнения
a (t ) a an
т.е. нормальное ускорение:
dτ
a .
dt
n
Быстрота
направления
изменения
касательной (dτ/dt ) к траектории определяется скоростью движения точки по
окружности и степенью искривленности
траекторий.
30
31.
Степень искривленности плоской кривойхарактеризуется кривизной С.
Радиус кривизны r
–
радиус
такой
окружности,
которая
сливается с кривой в
данной
точке
на
бесконечно
малом
ее
участке dS.
1
ΔS dS
r lim
.
C Δφ 0 Δφ dφ
31
32.
Нормальное ускорениепоказывает быстроту
изменения направления
вектора скорости
υ
a n,
r
2
n
Модуль нормального ускорения: a a
.
r
2
n
n
Центростремительным
называют
ускорение – когда движение происходит по
окружности. А когда движение происходит по
произвольной кривой – говорят, нормальное
ускорение, перпендикулярное к касательной в
любой точке траектории.
32
33.
Суммарный вектор ускорения придвижении точки вдоль плоской кривой равен:
dυ υ
a a a τ n.
dt
r
2
τ
n
aτ
v
a
Модуль общего ускорения равен:
a
r
an
2
2
aτ an
33
34.
Рассмотримнесколько
(частных) случаев:
предельных
a 0; an 0 – равномерное прямоли
нейное движение;
a const; an 0 – равноускоренное
прямолинейное движение;
a 0; a const – равномерное движение
n
по окружности.
34
35. Типы ускорений
Чтобы более наглядно представить свойствавведенных составляющих полного ускорения,
рассмотрим примеры движений частицы, при которых
эти составляющие возникают
Частица движется прямолинейно
vr
ar
aτ
vn
a
Частица движется по дуге окружности
r
an
35
36.
Вспомним несколько полезных формул(прямая задача кинематики) :
t
s υdt υt
При равномерном движении
0
При движении с постоянным ускорением
2
at
S υ 0t
.
2
υ υ0 at
36
37.
Обратнаязадача
кинематики
заключается в том, что по известному
значению ускорения a(t) найти скорость точки
и восстановить траекторию движения r(t).
d (t )
a (t )
,
dt
По определению
отсюда
t2
(t ) (t ) a(t )dt
0
t1
dr
или, так как (t )
,
dt
Следовательно
t2
r (t ) r (t ) (t )dt.
0
t1
38. 1.4. Кинематика твердого тела
Различают пять видов движения твердоготела:
- поступательное;
- вращательное вокруг неподвижной оси;
- плоское;
- вокруг неподвижной точки;
- свободное.
Поступательное
движение
и
вращательное движение вокруг оси –
основные виды движения твердого тела.
Остальные виды движения твердого тела можно
свести к одному их этих основных видов или к38 их
совокупности.
39. 1.4.1. Поступательное движение твердого тела
Поступательное движение – это такоедвижение твердого тела, при котором любая
прямая,
связанная
с
телом,
остается
параллельной своему начальному положению и при
этом, все точки твердого тела совершают
равные перемещения.
39
40.
Скорости и ускорения всех точек твердоготела в данный момент времени t одинаковы.
Это
позволяет
свести
изучение
поступательного движения твердого тела к
изучению движения отдельной точки, т.е. к
задаче кинематики материальной точки,
подробно рассмотренной в прошлом разделе.
40
41.
При вращательном движении всеточки тела движутся по окружностям,
центры которых лежат на одной и той же
прямой OO,' называемой осью вращения
(рисунок 2.3).
Из определения вращательного движения ясно,
что
понятие
вращательного
движения
для
материальной точки неприемлемо.
Рисунок 1.3
41
42. 1.4.2. Вращательное движение вокруг неподвижной оси
Движение твердого тела, при котором двеего точки О и О' остаются неподвижными,
называется вращательным движением вокруг
неподвижной оси, а неподвижную прямую ОО'
называют осью вращения.
Пусть абсолютно твердое
тело вращается вокруг
неподвижной оси ОО'
Рисунок 1.12
42
43.
Проследим за некоторой точкой М этоготвердого тела. За время dt
точка М совершает
элементарное перемещение
При том же самом угле поворота dφ другая
точка, отстоящая от оси на большее или меньшее
расстояния,
совершает
другое
перемещение.
Следовательно, ни само перемещение некоторой
точки твердого тела,
dr
ни первая производная
2
dr
ни вторая производная
dt
dt
2
не могут служить
характеристикой движения
всего твердого тела.
43
44.
Угол поворотаdφ характеризует перемещения всего тела за время dt (угловой путь)Удобно ввести dφ – вектор элементарного
поворота тела, численно равный dφ и направленный
вдоль оси вращения ОО' так, чтобы глядя вдоль
вектора dφ мы видели вращение по часовой стрелке
(направление вектора dφ
и направление вращения связаны
правилом буравчика).
Элементарные
повороты
удовлетворяют обычному правилу
сложения векторов:
dφ dφ dφ .
1
2
44
45.
Угловой скоростьюназывается вектор ω
численно равный первой
производной от угла поворота
по времени и направленный
вдоль оси вращения
в
направлении dφ ( ω и dφ
всегда направлены в одну
сторону).
dφ
ω
dt
dφ
ω .
dt
45
46.
Связь линейной и угловой скоростиПусть – линейная скорость точки М.
За промежуток времени dt точка М проходит
путь dr dt.
В
то
же
время
dr Rdφ (центральный угол). Тогда,
dr Rdφ
υ
ωR
dt
dt
υ ωR
46
47.
υ ωR - Связь линейной и угловой скоростиВ векторной форме - υ [ω, R ]
Вектор ортогонален к векторам ω и R
и направлен в ту
же
сторону,
что
и
векторное
произведение [ω, R ]
47
48.
Период Т – промежуток времени, втечение которого тело совершает полный
оборот (т.е. поворот на угол φ 2π )
2π
Т ;
ω
Частота ν – число оборотов тела за 1 сек.
1
ν .
Т
Угловая скорость
2π
ω
2 πν;
Т
48
49.
εВведем вектор углового ускорения
для
характеристики
неравномерного
вращения тела:
dω (2.4.3)
ε
dt
.
Вектор ε направлен в ту же
сторону, что и ω при ускоренном
вращении
dω
а ε
0
dt
направлен
в противопо
ложную сторону при замедленном
вращении
dω
0
dt
(рисунок 2.13).
49
50.
Выразим нормальное и тангенциальноеускорения точки М через угловую скорость и
угловое ускорение:
dυ d
dω
aτ
(ωR) R
Rε;
dt dt
dt
a R ;
υ
2
an
ω R.
R
2
4π R
2 2
an 2 4π ν R
T
2
50
51.
Формулы простейших случаев вращениятела вокруг неподвижной оси:
- равномерное вращение ε 0; ω const;
φ φ0 ωt ;
- равнопеременное
вращение
ε const ;
ω ω 0 εt
εt
φ ω 0t
2
2
51
52.
Обратите внимание.Все
кинематические
параметры,
характеризующие
вращательное
движение (угловое ускорение, угловая
скорость и угол поворота)
направлены вдоль оси
вращения.
52
53.
Связь между линейными и угловымивеличинами при вращательном движении:
s Rφ
υ R ω
a a τ an
a
2
2
a τ an
an υ R ω R
2
4π R
2 2
an 2 4π ν R
T
2
2
a τ R ε.
54.
5455. Тема 2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ.СИЛЫ В МЕХАНИКЕ. РАБОТА. ЭНЕРГИЯ.
56. 2.1. Первый закон Ньютона. Инерциальные системы
В основе так называемойклассической или ньютоновской
механики лежат три закона
динамики, сформулированных И.
Ньютоном в 1687 г. Эти законы
играют исключительную роль в
механике и являются (как и все
физические
законы)
обобщением
результатов
огромного человеческого опыта.
57.
Первый закон Ньютона:всякая
материальная
точка
сохраняет состояние покоя или
равномерного
прямолинейного
движения до тех пор, пока
воздействие со стороны других
тел не заставит её изменить
это состояние.
F 0, const или 0
(Закон инерции)
58.
Оба названных состояния схожи тем, чтоускорение тела равно нулю. Поэтому
формулировке первого закона можно придать
следующий вид: скорость любого тела
остаётся постоянной (в частности,
равной нулю), пока воздействие на это
тело со стороны других тел не вызовет
её изменения.
Стремление тела сохранить состояние
покоя или равномерного прямолинейного
движения называется инертностью.
Поэтому первый закон Ньютона называют
законом инерции.
59.
Механическое движение относительно, и егохарактер зависит от системы отсчёта. Первый закон
Ньютона выполняется не во всякой системе отсчёта,
а те системы, по отношению к которым он
выполняется,
называются
инерциальными
системами отсчёта.
Инерциальной системой отсчёта является
такая система отсчёта, относительно которой
материальная точка, свободная от внешних
воздействий, либо покоится, либо движется
прямолинейно и равномерно (т.е. с постоянной
скоростью).
Таким образом, первый закон Ньютона
утверждает
существование
инерциальных
систем отсчёта.
60.
Система отсчёта, связанная с Землей,строго говоря, неинерциальная, однако
эффекты,
обусловленные
её
неинерциальностью (Земля вращается вокруг
собственной оси и вокруг Солнца) при
решении многих задач малы, и в этих случаях
её можно считать инерциальной.
Из приведённых выше примеров легко
понять,
что
основным
признаком
инерциальной
системы
является
отсутствие ускорения.
61.
Сущность первого закона Ньютонаможет быть сведена к трём
основным положениям:
• все тела обладают свойствами инерции;
• существуют инерциальные системы
отсчёта, в которых выполняется первый
закон Ньютона;
• движение относительно.
(Если тело А движется относительно
тела отсчета В со скоростью υ, то и
тело В, в свою очередь, движется
относительно тела А с той же
скоростью, но в обратном направлении) .
62. 2.2. Масса и импульс тела
Воздействие на данное тело со стороныдругих тел вызывает изменение его скорости, т.е.
сообщает данному телу ускорение.
Опыт показывает, что одинаковое воздействие
сообщает разным телам разные по величине ускорения.
Всякое тело противится попыткам изменить
его состояние движения. Это свойство тел, как мы
уже говорили, называется инертностью (следует из
первого закона Ньютона).
Мерой инертности тела
величина, называемая массой.
является
Чтобы определить массу некоторого тела, нужно
сравнить её с массой тела, принятого за эталон массы
(или сравнить с телом уже известной массы).
63.
Масса – величина аддитивная (масса теларавна сумме масс частей, составляющих это
тело).
Система тел, взаимодействующих только
между собой, называется замкнутой.
Рассмотрим замкнутую систему двух тел
массами m1 и m2 Столкнём эти два тела
Рисунок 2.1
Опыт показывает, что приращённые скорости 1 и 2
всегда имеют противоположное направление (отличное
знаком), а модули приращений скорости относятся как:
64.
Δ mΔ m
1
2
2
1
(тело, обладающее
большей массой, меньше изменяет скорость).
Приняв во внимание направление скоростей, запишем:
m Δ m Δ .
1
1
2
2
При c масса m const
классическая механика), тогда имеем:
(ньютоновская,
Δ m Δ m .
1
1
2
2
Произведение массы тела m на скорость
называется импульсом тела p :
p m .
(2.2.2)
65. 2.3. Второй закон Ньютона.
Математическое выражение второго законаНьютона:
dp
dt
F
(2.3.1)
скорость изменения импульса тела равна
действующей на него силе.
,
dp Fd t
Отсюда можно заключить, что
изменение импульса тела равно импульсу силы.
Из (3.3.1), получим выражение второго закона через
ускорение a :
d
d
d m
a,
F. т. к. m const то m dt F. но
dt
dt
тогда ma F
66.
основное уравнение динамики постуma
F
пательного движения материальной точки.
Принцип суперпозиции или принцип
независимости действия сил
Если на материальное тело действуют
несколько сил, то результирующую силу
можно найти из выражения:
(2.3.3)
n
F Fi ,
i 1
F F
a
a ,
Из второго закона Ньютона, имеем
m m
где a – ускорение тела, под действием силы F . Отсюда,
.
(2.3.4)
a a
n
i 1
i
n
i 1
i
i
n
i 1
i
i
67.
a an
i 1
i
Если на материальную точку действует
несколько сил, то каждая из них сообщает точке
такое же ускорение, как если бы других сил не
было.
Найдем изменение импульса тела за
конечный промежуток времени
m m FΔt ,
2
1
Δ mυ F dt
t2
t1
(2.3.5)
т.е., изменение импульса тела равно импульсу силы.
68.
В системе СИ семь основных единиц(м) – метр,
(кг) – килограмм,
(с) – секунда,
(А) – ампер,
(К) – кельвин,
(кд) – кандела (единица силы света),
(кмоль) – единица количества вещества.
Остальные единицы производные
получаются из физических законов связывающих их
с основными единицами. Например из второго
закона Ньютона производная единица силы
1 кг·м/с2 = 1 Н.
69. 2.4. Третий закон Ньютона
Действие телвзаимодействия.
друг
на
друга
носит
характер
Третий закон Ньютона отражает тот
факт, что сила есть результат взаимодействия
тел, и устанавливает, что силы, с которыми
действуют друг на друга два тела, равны
по величине и противоположны по
направлению.
.
(2.4.1)
F12 F21
70. 2.9. Третий закон Ньютона
Взаимодействующие тела действуют друг надруга с одинаковыми по величине, но
противоположными по направлению силами:
F12 F21
Законы Ньютона сформулированы в 1687 г., играют исключительную
роль в механике и являются обобщением результатов огромного
человеческого опыта. Их рассматривают как систему взаимосвязанных
законов и опытной проверке подвергают не каждый закон в
отдельности, а всю систему в целом.
71.
3-й Закон Ньютона в общем случае являетсяуниверсальным законом взаимодействий:
Всякое действие вызывает равное по величине противодействие
F12 F21
Подчеркнем, что силы,
связанные по 3 закону
Ньютона, приложены к различным телам и,
следовательно, никогда не могут начинаться в одной
точке
F12
F21
72. 2.5. Импульс произвольной системы тел
Центр инерции или центр масс системыматериальных точек называют такую точку С
(рисунок 3.2), радиус-вектор которой:
m r 1
r
m r,
m
m
n
i 1
c
где m i 1 mi
системы.
n
i
i
n
i 1
n
i 1
i
i
(2.5.1)
i
– общая масса системы, n – число точек
Рисунок 3.2
73. Центр масс
Воображаемую точку С радиус-вектором1 n
rc ri mi
m i 1
где i - номер точки,
n - количество точек,
mi - масса i-ой точки и
m - масса всей системы точек
называют центром масс
системы материальных
точек
Z
K
O
X
rc
Y
74.
Величинаpi mi υi
является первым динамическим
параметром частицы и
называется импульсом
Z
n
Pc m v c mi v i
K
называют импульсом центра
масс
O
Соответственно
величину
i 1
Таким образом видим, что
связь импульса Pc со
скоростью vc такая же, как
для материальной точки
с массой m (масса системы)
X
rc
Y
75. 2.6. Основное уравнение динамики поступательного движения произвольной системы тел
Тела, не входящие в состав рассматриваемойсистемы, называют внешними телами, а силы,
действующие на систему со стороны этих тел –
внешними силами. Силы взаимодействия между
телами внутри системы, называют внутренними
силами.
Результирующая всех внутренних сил
действующих на i-ое тело:
внутр. n
Fi
Fik Fi1 Fi 2 ... Fin ,
k i
где
k i – т.к. i-ая точка не может действовать сама на себя.
76.
Fвнеш.
Обозначим
– результирующая всех
внешних сил приложенных к i-ой точке системы.
По второму закону Ньютона можно записать
систему уравнений:
i
внеш.
d
m1υ1 F1 F12 F13 ... F1n ,
dt
внеш.
d
m2 υ2 F2 F21 F23 ... F2 n ,
dt
...............................,
внеш.
d
mn υn Fn Fn1 ... Fn,n 1.
dt
77.
Сложим эти уравнения и сгруппируем попарно силы F и F :ik
ki
n
d
внеш.
dt mi υi Fi F12 F21 ... Fn 1,n Fn,n 1 .
i 1
i 1
n
По третьему закону Ньютона, F F
поэтому все выражения в скобках в правой части
уравнения равны
нулю. Тогдаn остаётся:
n
ik
ki
внеш. dp
d
dt mi υi Fi dt .
i 1
i 1
n внеш.
Назовем F Fi
– главным вектором всех
внешних сил, i 1
тогда:
dp
F.
dt
(2.6.1)
78.
Скорость изменения импульса системы тел равнаглавному вектору всех внешних сил, действующих
на эту систему.
Это уравнение называют основным уравнением
динамики поступательного движения системы
тел.
Так как импульс системы
p m
d
m F
dt
dp
F
dt
c
то
c
Отсюда можно записать основное уравнение
динамики
поступательного
движения
системы тел в виде:
Здесь a
c
mac F
– ускорение центра инерции.
(2.6.3)
79.
mac F Центр механической системыдвижется как материальная точка, масса
которой равна массе всей системы, и на
которую действует сила, равная главному
вектору внешних сил, приложенных к системе.
На основании третьего закона Ньютона,
силы, действующие на тела системы со стороны
других тел системы (внутренние силы),
взаимно
компенсируют
друг
друга.
Остаются только внешние силы.
В общем случае движение тела можно
рассматривать как сумму двух
движений:
поступательного со скоростью υ υС
и
вращательного вокруг центра инерции.
80. Теорема о движении центра масс
Рассмотрим подробнее силы, действующие на частицы механическойсистемы
Силы, действующие на каждую точку
системы, разобьем на два типа
– внутренние силы
– результирующая всех внешних сил
В общем виде это можно записать так:
n 1
Fi Fik Fi вн
k 1
По 3 закону Ньютона Fik 0
i ,k
F1i
m2
m3
F13
F12
m1
(F1)вш
1 n
ac Fi вн
m i 1
mi
И теорема о движении центра
масс принимает вид
Если система находится во внешнем стационарном и
однородном поле, то никакими действиями внутри системы
невозможно изменить движение центра масс системы
81. 2.7. Закон сохранения импульса
Механическаясистема
называется
замкнутой (или изолированной), если на неё не
действуют внешние силы, т.е. она не
взаимодействует с внешними телами.
Строго говоря, каждая реальная система тел всегда
не замкнута, т.к. подвержена, как минимум воздействию
гравитационных сил. Однако если внутренние силы гораздо
больше внешних, то такую систему можно считать
замкнутой (например – Солнечная система).
Для замкнутой системы равнодействующий
вектор внешних сил тождественно равен нулю:
dp
F 0,
dt
(2.7.1)
82.
nотсюда
p mi υc const.
(2.7.2)
i 1
Это есть закон сохранения импульса: импульс
замкнутой системы не изменяется во времени.
Импульс системы тел может быть представлен в виде
произведения
массы тел на скорость центра
суммарной
инерции: p m c , тогда
m c const.
(2.7.3)
При любых процессах, происходящих в
замкнутых системах, скорость центра инерции
сохраняется неизменной.
Закон сохранения импульса является одним из
основных законов природы. Он был получен как следствие
законов Ньютона, но он справедлив и для микрочастиц и
для релятивистских скоростей, когда
c
83. 2.8. Виды и категории сил в природе
Одно из простейших определений силы:влияние одного тела (или поля) на другое,
вызывающее ускорение – это сила.
Однако, спор вокруг определения силы не
закончен до сих пор – это обусловлено трудностью
объединения в одном определении
сил,
различных по своей природе и характеру
проявления.
83
84.
В настоящее время,различают четыре типа сил или
взаимодействий:
• гравитационные;
• электромагнитные;
• сильные (ответственное за
связь частиц в ядрах) и
• слабые (ответственное за
распад частиц)
84
85. I. Силы
dp ddv
F
mv m
ma
dt dt
dt
• Силы трения
• Силы тяготения (гравитационные силы)
• Силы тяжести (вес тела)
• Силы упругости
86. 2.9. Сила тяжести и вес тела
Одна из фундаментальных сил – силагравитации проявляется на Земле в виде силы
тяготения – сила, с которой все тела
притягиваются к Земле.
Вблизи поверхности Земли все тела падают
с одинаковым ускорением – ускорением
свободного падения g, (вспомним школьный опыт
– «трубка Ньютона»). Отсюда вытекает, что в
системе отсчета, связанной с Землей,
на всякое
тело действует сила тяжести mg
Она приблизительно равна силе гравитационного притяжения к
Земле (различие между силой тяжести и гравитационной силой
обусловлено тем, что система отсчета, связанная с Землей, не 86
вполне инерциальная).
87.
то есть вес и сила тяжести равны другдругу, но приложены к разным точкам: вес к
подвесу или опоре, сила тяжести – к самому
телу. Это равенство справедливо, если подвес
(опора) и тело покоятся относительно Земли (или
двигаются равномерно, прямолинейно). Если
имеет место движение с ускорением, то
справедливо соотношение:
P mg ma m( g a).
(2.9.1)
87
88.
P mg ma m( g a).Вес тела может быть больше или
меньше силы тяжести: если g и a
направлены в одну сторону (тело
движется вниз или падает), то
P mg
и если наоборот, то P mg
Если же тело движется
с
ускорением a g то P 0
–
т.е.
наступает
состояние
невесомости.
Пример: космический корабль на орбите.
88
89. 2.10. Упругие силы
Электромагнитные силы проявляютсебя как упругие силы и силы трения.
Под действием внешних сил возникают
деформации (т.е. изменение размеров и формы)
тел. Если после прекращения действия внешних
сил восстанавливаются прежние форма и
размеры тела, то деформация называется
упругой. Деформация имеет упругий характер в
случае, если внешняя сила не превосходит
определенного значения, которая называется
пределом упругости.
89
90.
При превышении этого предела деформациястановится
пластичной
или
неупругой,
т.е.
первоначальные размеры и форма тела полностью не
восстанавливается.
Рассмотрим упругие деформации.
В деформированном теле (рис) возникают упругие
силы, уравновешивающие внешние силы.
90
91.
Под действием внешней силы – Fвн. пружинаполучает удлинение x, в результате в ней возникает упругая сила – Fупр, уравновешивающая Fвн.
Упругие
силы
возникают
во
всей
деформированной
пружине.
Любая
часть
пружины действует на другую часть с силой
упругости Fупр.
91
92.
Удлинение пружины пропорционально внешнейсиле и определяется законом Гука:
1
x Fвн. ,
k
k – жесткость пружины.
Видно, что чем больше k, тем меньшее удлинение
получит пружина под действием данной силы.
92
93.
Так как упругая сила отличается отвнешней только знаком, т.е.
F F
упр .
вн.
то закон Гука можно записать в виде:
F kx.
упр.
93
94.
Потенциальная энергия упругойпружины U равна работе, совершенной
над пружиной.
Так как сила не постоянна, то
элементарная работа равна dA Fdx
dA kxdx,
Тогда полная работа,
совершена пружиной, равна:
x
которая
kx
A dA kxdx
2
0
2
kx
U
2
2
94
95.
Закон Гука для стержняОдностороннее
(или
продольное)
растяжение (сжатие) стержня состоит в
увеличении
(уменьшении)
длины
стержня под действием внешней силы F
95
Рисунок 2.3
96.
Такаядеформация
приводит
к
возникновению в стержне упругих сил, которые
принято характеризовать напряжением σ:
F
σ ,
S
упр.
2
π
d
Здесь S
4
– площадь
поперечного
сечения стержня, d – его диаметр.
В
случае
растяжения
σ
считается
положительной,
а
в
случае
сжатия
–
отрицательной.
Опыт
показывает,
что
приращение длины стержня l пропорционально
96
напряжению σ:
97.
Приращение длины стержня lпропорционально напряжению σ:
1
Δl .
k
Коэффициент пропорциональности k, как и
в случае пружины, зависит от свойств материала
и длины стержня.
Доказано, что
E
k
l
где
Е–
величина, характеризующая упругие
свойства материала стержня – модуль
Юнга.
Е - измеряется в Н/м2 или в Па.
97
0
98.
приращение длины:l
Δl ,
E
0
Δl
ε – относительное приращение длины,
l
0
1
ε σ
E
(2.10.2)
Закон
Гука
для
стержня:
относительное
приращение
длины
стержня
прямо
пропорционально
напряжению и обратно пропорционально
98
модулю Юнга.
99.
Растяжениеили
сжатие
стержней
сопровождается
соответствующим
изменением их поперечных размеров
Отношение относительного поперечного
Δd
d
сужения
(расширения)
стержня
к относительному
удлинению (сжатию) Δl
называют коэффициентом Пуассона
l
Δd Δl
M
: .
d l
99
(2.10.3)
100.
Объемная плотность потенциальнойэнергии тела
σ при растяжении
(сжатии) определяется удельной работой
по преодолению упругих сил Aупр
рассчитанной на единицу объема тела:
ω
σ
ωσ Aупр.
.
2E
2
(2.10.4)
100
101.
Деформация сдвигаИзгиб
102.
Деформация сдвигаF приложенной
Под действием силы
касательно к верхней грани, брусок
получает
деформацию сдвига
Пусть АВ – плоскость сдвига
102
Рисунок 2.4
103. 2.11. Силы трения
Трение подразделяется на внешнее ивнутреннее.
Внешнее
трение
возникает
при
относительном
перемещении
двух
соприкасающихся
твердых
тел
(трение
скольжения или трение покоя).
Внутреннее трение наблюдается при
относительном перемещении частей одного и
того же сплошного тела (например, жидкость
или газ).
103
104.
Различают сухое и жидкое (или вязкое) трение.Жидким (вязким) называется трение
между
твердым
телом
и
жидкой
или
газообразной средой или ее слоями.
Сухое
трение,
в
свою
очередь,
подразделяется на трение скольжения и
трение качения.
104
105.
Установлено, что максимальная сила тренияпокоя не зависит от площади соприкосновения тел и
приблизительно пропорциональна модулю силы
нормального давления N
F μ N,
0
0
μ0 – коэффициент трения покоя – зависит от
природы и состояния трущихся поверхностей.
Аналогично и для силы трения скольжения:
F μN
тр.
.
(2.11.1)
Трение
качения
возникает
между
шарообразным телом и поверхностью, по которой
оно катится. Сила трения качения подчиняется тем же
законам, что и скольжения, но коэффициент трения μ здесь
105
значительно меньше.
106.
106107. 2.12. Кинетическая энергия.
Уравнениедвижения
тела под
действием внешней силы F имеет вид:
d
m
F, или
dt
dυ
m Fτ .
dt
(2.12.1)
108.
dυm Fτ .
dt
Умножим обе части этого равенства на
dt dr , получим: mυ dυ Fτ dr.
Левая часть равенства, есть полный
дифференциал некоторой функции:
m
m d d
2
2
m
d
F
d
r
.
или
2
2
τ
109.
Функциясостояния
системы,
определяемая только скоростью ее
движения, называется кинетической
энергией.
2
m
K
.
2
(2.12.2)
Кинетическая энергия системы есть
функция состояния движения этой системы.
K – аддитивная величина:
m
K
,
2
2
n
i
i 1
i
110.
Энергия измеряется в СИ в единицахпроизведения силы на расстояние, т.е.
в ньютонах на метр: 1 Н м 1Дж
Кроме того, в качестве единицы
измерения
энергии
используется
внесистемная единица – электронвольт (эВ): 1 эВ = 1,6 10-19 Дж.
111.
Связь кинетической энергии с импульсом p.m m m
,
2 m 2m
2
Т.к.
2
p
K
.
2m
2
2
отсюда
112.
Связь кинетической энергии с работой.Если постоянная сила действует на
тело, то оно будет двигаться в направлении
силы. Тогда, элементарная работа по
перемещению тела из т. 1 в т. 2, будет равна
произведению силы F на перемещение dr :
dA Fdr
113.
Следовательно,работа
силы
приложенной к телу на пути r численно
равна изменению кинетической энергии
этого тела:
(2.12.4)
A K .
Или
изменение
кинетической
энергии dK равно работе внешних сил:
dK dA.
Работа, так же как и кинетическая
энергия, измеряется в джоулях.
114.
Скорость совершения работы (передачиэнергии) называется мощность.
Мощность
есть
работа,
совершаемая в единицу времени.
Мгновенная
или
мощность
dr
N F F .
dt
Средняя мощность
dA
N
dt
A
N .
t
Измеряется мощность в ваттах. 1 Вт = 1 Дж/с.
115.
Силы, работа которых не зависитот пути, по которому двигалось тело, а
зависит от начального и конечного
положения
тела
называются
консервативными.
Обозначим A – работа консервативных
сил, по перемещению тела из т. 1 в т. 2
Рисунок 12.2
116.
Еслициркуляция
какого-либо
вектора силы равна нулю, то эта сила
консервативна.
Консервативные силы: сила тяжести,
электростатические силы, силы центрального
стационарного поля.
Неконсервативные силы: силы
трения, силы вихревого электрического поля.
Консервативная система – такая,
внутренние
силы
которой
только
консервативные, внешние – консервативны
и стационарны.
Пример
консервативных
сил
–
гравитационные силы.
117. 2.13. Потенциальная энергия
Если на систему материальных телдействуют консервативные силы, то
можно ввести понятие потенциальной
энергии.
Работа, совершаемая консервативными
силами при изменении конфигурации
системы, то есть при изменении положения
тел относительно системы отсчета, не
зависит от того, как было осуществлено это
изменение. Работа определяется только
начальной и конечной конфигурациями
системы:
118.
A U U ,12
1
2
(2.13.1)
здесь потенциальная энергия U (х, у, z) –
функция состояния системы, зависящая
только от координат всех тел системы
в поле консервативных сил.
Итак, K – определяется скоростью
движения тел системы, а U – их взаимным
расположением.
Из (2.13.1) следует, что работа
консервативных
сил
равна
убыли
потенциальной энергии:
dA dU .
119.
Потенциальная энергия упругойдеформации (пружины)
Найдём работу, совершаемую при
деформации упругой пружины.
Сила упругости Fупр kx,
Сила
непостоянна, поэтому элементарная работа
dA Fdx kxdx
знак минус говорит о том, что работа
совершена над пружиной.
kx kx
A dA kxdx
,
2
2
x2
x1
2
2
1
2
(2.13.4)
120. 2.14. Закон сохранения механической энергии
Закон сохранения сводит воединорезультаты, полученные нами раньше.
В сороковых годах девятнадцатого века
трудами Р. Майера, Г. Гельмгольца и Дж.
Джоуля (все в разное время и независимо
друг от друга) был доказан закон
сохранения и превращения энергии.
121.
Для консервативной системычастиц полная энергия системы:
E K U
внутр.
U
Для
механической
сохранения
звучит
внеш .
const
энергии
закон
так:
полная
механическая
энергия
консервативной системы материальных
точек остаётся постоянной.
122.
Для замкнутой системы,т.е. для системы на которую не действуют
внешние силы, можно записать:
(2.14.2)
E K U
т.е. полная
внутр.
const
механическая энергия
замкнутой системы материальных
точек, между которыми действуют
только
консервативные
силы,
остаётся постоянной.
123.
Если в замкнутой системе действуютнеконсервативные силы, то полная
механическая энергия системы не
сохраняется – частично она переходит в
другие виды энергии – неконсервативные.
Система, в которой механическая
энергия переходит в другие виды
энергии, называется
диссипативной,
а сам процесс перехода называется
диссипацией энергии.
124. Применение законов сохранения . Абсолютно упругий центральный удар
При абсолютно неупругом ударе законсохранения механической энергии не
работает.
Применим
закон
сохранения
механической энергии для расчета скорости
тел при абсолютно упругом ударе – это
такой удар, при котором не происходит
превращения механической энергии в
другие виды энергии.
125. Удар частиц
Ударом точечных частиц будем называтьтакое механическое взаимодействие
- при непосредственном контакте
- за бесконечно малое время
при котором частицы обмениваются
- энергией и
- импульсом
при условии, что
система частиц остается замкнутой
--------------------------------------------------------Различают два вида ударов
абсолютно неупругий удар
такой удар, при котором после удара частицы
движутся как единое целое
и абсолютно упругий удар
удар, при котором после удара частицы
движутся с различными скоростями и в
течении удара выполняются законы сохранения
(энергии и импульса)
p'1
E12
p'2
E21
Абсолютно упругий удар бывает двух типов
- нецентральный удар
- центральный удар
126.
Пример 1. Абсолютно-упругий центральный ударРазберем на ВК
Рисунок 2.7
На рисунке 2.7 изображены
два
шара
m1 и m2. Скорости шаров 1 2 (поэтому,
хотя скорости и направлены в одну сторону
все равно будет удар).
Систему можно считать замкнутой.
Кроме того, при абсолютно упругом ударе
она консервативна.
127.
Обозначим '1 и '2– скорости
шаров после их столкновения.
В данном случае можно воспользоваться
законом
сохранения
механической
энергии и законом сохранения импульса
(в проекциях на ось x):
m m m ' m '
2
2
2
2
m m m ' m '.
2
1
1
1
1
2
2
2
2
2
2
1
1
1
1
2
2
2
2
2
По ЗСЭ
По ЗСИ
128.
Пример 2. Абсолютно упругий ударшара о неподвижную массивную стенку.
Стенку
можно
рассматривать
как
неподвижный шар с 2 0 массой m2
Разделим числитель и знаменатель на m2
и пренебрежем m1 / m2 тогда
m
2 1
m
2
'
,
m
1
1
m
1
2
1
2
1
1
2
2
1
т.е.
129. Пример 3. Абсолютно неупругий удар
Абсолютно неупругий удар –это столкновение двух тел, в
результате
которого
тела
объединяются и двигаются дальше,
как единое целое.
Продемонстрировать
абсолютно
неупругий удар можно с помощью
шаров
из
пластилина
(глины),
движущихся навстречу друг другу.
υ2
m2
130.
Если массы шаров m1 и m2, их скоростидо удара 1 и 2
то используя закон
сохранения импульса, можно записать
–
m m (m m )
1
1
2
2
1
2
скорость движения
неупругого удара:
m m
.
m m
1
1
2
1
2
2
шаров
после
131.
Итак, скорость слипшихсяшаров после неупругого удара
m m
.
m m
1
1
2
1
2
2
Если шары двигались навстречу друг
другу, то они вместе будут продолжать
двигаться в ту сторону, в которую двигался
шар, обладающий большим импульсом.
В частном случае, если массы и
скорости шаров равны, то
1
2
2
0
Выясним, как меняется кинетическая
энергия
шаров
при
центральном
абсолютно неупругом ударе.
132.
«Потеря» кинетической энергии,(диссипация энергии).
m m (m m )
K
2
2
2
2
1
2
1
2
2
1
2
2
Отсюда, получаем
mm
.
K
2(m m )
(5.6.3)
Если
ударяемое
тело
первоначально неподвижно 2 0
было
то
1
2
2
1
1
2
2
m
m m
, K
.
m m
m m 2
2
1
1
1
2
2
1
1
2
1
133. Тема 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
133134. 3.1. Динамика вращательного движения твердого тела относительно точки
rРассмотрим твердое тело, как некую систему (рис.),
состоящую из n точек (m1 m2 … mn);
– радиус-вектор i-ой
i
точки, проведенный из точки О – центра неподвижной
инерциальной системы отсчета.
Обозначим
F – внешняя сила, действующая на i-ю точку,
F – сила действия со стороны k-ой точки на i-ю.
i
ik
134
135.
Запишем основное уравнение динамикидля точки
d
m F F .
dt
n
i
i
k 1
k i
Рисунок 3.1
ik
i
135
136.
Векторное произведение r точкина её импульс
называется моментом
импульса L этой точки относительно
точки О.
(3.1.1)
L r , m .
i
i
i
i
i
i
Эти три вектора образуют правую
тройку векторов, связанных «правилом
буравчика»:
136
Рисунок 3.2
137.
Векторноепроизведение
r
проведенного в точку приложения сил, на
эту силу называется моментом силы M :
i
M [ r , F ],
i
(3.1.2)
Обозначим li – плечо силы Fi, (рис.3.3). Т.к
i
i
i
sin(180 ) sin
то:
M F r sin Fl ,
i
i
i
(3.1.3)
i i
137
138.
C учетом новых обозначений:dL
M M
dt
n
(3.1.4)
i
ik
k 1
i
Запишем систему n уравнений для
всех точек системы и сложим, левые и
правые части уравнений:
dL
M M .
dt
то M 0.
Так как F F
n
n
n
i 1
k 1
n
i
i 1
ik
ki
ik
i
i 1
n
n
i 1
k 1
ik
138
139.
Здесь суммапроизводной суммы:
производных
dL
dL
,
dt
dt
равна
n
i
где
L – момент
i 1
импульса системы,
M – результирующий момент всех
внешних сил относительно точки О.
Окончательно получим:
dL
M
dt
внеш
139
140.
dLM
dt закон
внеш
Основной
динамики
вращательного движения твердого тела,
вращающегося вокруг точки.
Момент импульса системы L
является
основной
динамической
характеристикой
вращающегося тела.
Сравнивая это уравнение с основным уравнением
динамики поступательного движения, мы видим их внешнее
сходство
dp
F.
dt
140
141. 3.2. Динамика вращательного движения твердого тела относительно оси
Описанное нами движение твердоготела относительно неподвижной точки
является основным видом
движения.
Однако вычислить вектор L
– момент
импульса
системы
относительно
произвольной точки не просто: надо знать
шесть проекций (три задают положение
тела, три задают положение точки).
Значительно
проще найти момент
импульса L тела, вращающегося вокруг
141
неподвижной оси (z) (рисунок 3.4).
142.
Пусть некоторое теловращается вокруг оси z
Получим уравнение динамики
для некоторой точки mi этого
тела находящегося на расстоянии Ri от оси
вращения. При этом помним, что L z и M z
направлены всегда вдоль оси вращения z,
поэтому в дальнейшем опустим значок z.
dL
M
dt
или
i
i
d
[ R, m ] M
dt
i
142
i
143.
Так как i у всех точекразная, введем, ω
вектор угловой скорости
причем
ω .
R
d
m R ω M
dt
2
Тогда
i
i
i
Так как тело абсолютно твердое, то в
процессе вращения mi и Ri останутся
неизменными. Тогда:
dω
mR
M.
dt
2
i
i
i
143
144.
Обозначим Ii – моментинерции точки находящейся
на расстоянии R от оси
вращения:
2
I i mi Ri . (3.2.1)
Так как тело состоит из огогромного количества точек и все
они находятся на разных расстояниях от
оси вращения, то момент инерции тела
m
равен:
2
(3.2.2)
I R dm,
0
где R – расстояние от оси z до dm.
Как видно,
скалярная.
момент
инерции
I
–
величина
144
145.
Просуммировав (3.2.1) повсем i-ым точкам,
получим
или
dω
I
M
dt
Iε M
(3.2.3)
Это основное уравнение динамики
тела
вращающегося
вокруг
неподвижной оси. (Сравним: ma F
–
основное
уравнение
динамики
поступательного движения тела).
Idω Mdt ; Idω dL
L Iω
145
146.
LI
ω
(3.2.4)
Где L – момент импульса
тела вращающегося вокруг
оси z
(Сравним: p m для
поступательного движения).
При этом помним, что L и M динамические
характеристики вращательного движения
направленные
всегда вдоль оси вращения.
Причем, L определяется
направлением
вращения, как и ω а M – зависит от того,
ускоряется или замедляется вращение. 146
147. Повторим основные характеристики вращательного движения
Эти формулы получены для однойточки вращающегося твердого
тела
Li J i z ω Момент импульса
Момент силы
M i Ji zε
Суммируя
по всему телу, получим
n
J i z mi ri
Lz Li J z ω Момент импульса
2 Момент инерции
твердого тела
i 1
n
M z M i J z ε Момент силы
твердого тела
i 1
n
J z Ji z
i 1
Момент инерции
твердого тела
Основной закон динамики вращательного движения
твердого тела
Z
Li|z
ω
ri
Mi
K
147
148.
3.3.Расчет
моментов
инерции
некоторых
простых
тел.
Моменты инерции шара, сферы, диска,
обруча и стержня приведены на рис. 3.6.
Шар
Стержень
Диск
k 2 5;
k 1 2;
2
I 2 5 m R ; Ic 1 2 m R ;
2
c
Сфера
I 2 3 m R ;
2
c
Обруч
I m R
c
2
1
k
12
1
I ml
12
c
148
2
149.
Теорема ШтейнераПри вычислении момента
инерции тела, вращающегося
вокруг оси, не проходящей
через центр инерции, следует
пользоваться теоремой о
параллельном переносе осей
или теоремой Штейнера
(Якоб Штейнер, швейцарский
геометр 1796 – 1863 гг.).
I I md
c
Z
ω
Y
X
2
ri
K
ε
149
150.
Теорема ШтейнераI I c md
2
Момент инерции тела I
относительно любой оси вращения равен
моменту его инерции I c
относительно
параллельной
оси,
проходящей через центр масс С тела,
плюс произведение массы тела на
150
квадрат расстояния между осями.
151.
Пример: стержень массойm, длиной l, вращается
вокруг оси, проходящей
через конец стержня (рис).
1 2
I c ml
12
2
1
1 2 1 2
l
I z I c m ml ml ml .
4
3
2 12
151
152. 3.4. Кинетическая энергия вращающегося тела
Кинетическая энергия – величинааддитивная, поэтому кинетическая энергия
тела, движущегося произвольным образом,
равна сумме кинетических энергий всех n
материальных точек, на которое это тело
можно мысленно разбить:
m
K
.
2
2
n
i
i
(3.4.1)
i 1
152
153.
mКинетическая энергия поступательного движения K
.
2
Если тело вращается
вокруг неподвижной оси z с
угловой
скоростью ω то линейная скорость i-й точки
2
n
i
i
i 1
υi ωRi
тогда
mi υi
ω
Iω
2
Kвращ.
mi Ri
.
2
2 i 1
2
i 1
n
2
2
n
2
Следовательно,
Iω
K вращ.
.
2
2
Сопоставив эти формулы можно увидеть, что
момент инерции тела I – является мерой инертности
при вращательном движении. Так же как масса m – 153
мера
инерции при поступательном движении.
154.
В общем случае движение твердого теламожно представить в виде суммы двух
движений
–
поступательного
со
скоростью
и вращательного
с
c
угловой скоростью
вокруг мгновенной
оси, проходящей через центр инерции.
Полная кинетическая энергия этого
тела:
2
2
m c Ic
.
(3.4.3)
K
полн.
2
2
Здесь Ic – момент инерции относительно
мгновенной оси вращения, проходящей через
154
центр инерции.
155.
mυIω
mgh
2
2
2
2
155
156. 3.5. Закон сохранения момента импульса
Для замкнутойсистемы тел момент
внешних сил М всегда равен нулю, так
как внешние силы вообще не действуют на
замкнутую систему:
dL
M 0
dt
отсюда
L const, или Iω const
Закон сохранения момента импульса
156
157.
Закон сохранения момента импульса– момент импульса замкнутой системы
тел относительно любой неподвижной
точки не изменяется с течением
времени.
Это один из фундаментальных законов
природы.
Аналогично для замкнутой системы
вращающихся вокруг оси z:
dL
M 0, отсюда L const или
dt
I ω const
z
z
z
157
z
158. 3.7. Сходство и различие линейных и угловых характеристик движения
Формулы кинематики и динамикивращательного
движения
легко
запоминаются, если сопоставить их с
формулами
поступательного
движения
(см. таблицу 3.1).
158
159.
Поступательное движениеdφ
ω
dt
dω
ε
dt
ω ω 0 εt
dS
υ
dt
dυ
a
dt
υ υ0 at
2
at
S υ 0t
2
t
S υdt
0
Вращательное движение
εt
φ ω 0t
2
2
t
φ ωdt
0
159
160.
dpF
dt
ma F
p m
m const
A FS
N Fv
m
mgh const
2
2
dL
M
dt
Iε M
L Iω
Iω const
A M
N Mw
Iω
mgh const
2
2
160
161.
161162.
162163. Тема 4. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
Тема 4. МОЛЕКУЛЯРНОКИНЕТИЧЕСКАЯ ТЕОРИЯ164. 4.1. Основные понятия и определения молекулярной физики и термодинамики
• Совокупностьтел,
составляющих
макроскопическую
систему,
называется
термодинамической системой.
• Система может находиться в различных
состояниях. Величины, характеризующие
состояние
системы,
называются
параметрами
состояния:
давление
P,
температура T, объём V и так далее. Связь
между P, T, V специфична для каждого тела и
называется уравнением состояния.
165. Под идеальным газом мы будем понимать газ, для которого: 1) радиус взаимодействия двух молекул много меньше среднего расстояния
междуними (молекулы взаимодействуют только
при столкновении);
2) столкновения молекул между собой и со
стенками сосуда – абсолютно упругие
(выполняются законы сохранения энергии и
импульса);
3) объем всех молекул газа много
меньше объема, занятого газом.
166. 4.2. Давление. Основное уравнение молекулярно-кинетической теории
Рассмотрим подробнее, что представляетсобой один из основных параметров
состояния – давление P.
Ещё в XVIII веке Даниил Бернулли
предположил, что давление газа – есть
следствие столкновения газовых
молекул со стенками сосуда.
Именно давление чаще всего является
единственным сигналом присутствия газа.
167. Итак, находящиеся под давлением газ или жидкость действуют с некоторой силой на любую поверхность, ограничивающую их объем. В
этом случае сила действует понормали к ограничивающей объем
поверхности. Давление на поверхность
равно:
ΔF
P
ΔS
где ΔF – сила, действующая на поверхность
площадью ΔS.
168. Внутреннее давление является одним и тем же во всех направлениях, и, во всем объеме независимо от формы сосуда. Этот результат
называется закономПаскаля: если к некоторой части
поверхности, ограничивающей газ или
жидкость, приложено давление P0, то
оно одинаково передается любой части
этой поверхности.
169. Таким образом, мы определили давление, как силу, действующую в единицу времени на единицу площади: (4.2.2)
P dF / dS.или
1
2
P m0 υ x
3
170.
Наивно полагать, что все молекулы подлетают кстенке S с одной и той же скоростью (рисунок 8.3). На
самом деле молекулы имеют разные скорости,
направленные в разные стороны, то есть скорости
газовых молекул – случайная величина.
Более точно
случайную величину
характеризует
среднеквадратичная
величина:
2
υx
171. Под скоростью понимаем среднеквадратичную скорость Вектор скорости, направленный произвольно в пространстве, можно разделить на
2Под скоростью υ x
понимаем
2
среднеквадратичную скорость υ x
Вектор скорости, направленный
произвольно в пространстве, можно разделить
на три составляющих:
υ
2
2
2
2
υ x υ y υ z .
Ни одной из этих проекций нельзя отдать
предпочтение из-за хаотичного теплового
движения молекул, то есть в среднем
2
2
2
υx υ y υz
.
172. Следовательно, на другие стенки будет точно такое же давление. Тогда можно записать в общем случае: или (4.2.3) где – средняя
Следовательно, на другие стенки будет точнотакое же давление. Тогда можно записать в общем
случае:
2
или
1
2 m0 υ
2
P m0 n υ n
,
3
3
2
2
P n Ek
3
(4.2.3)
где E k – средняя энергия одной молекулы.
Это основное уравнение молекулярно-
кинетической теории газов.
Итак, давление газов определяется средней
кинетической энергией поступательного
движения молекул.
173. Единицы измерения давления. По определению, поэтому размерность давления 1 Н/м2 = 1Па; 1 атм.= 9,8 Н/см2 = 98066 Па 105 Па 1
Единицы измерения давления.F
По определению, P , поэтому
S
размерность давления
Н
.
2
м
1 Н/м2 = 1Па;
1 атм.= 9,8 Н/см2 = 98066 Па 105 Па
1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па
1 бар = 105 Па;
1 атм. = 0,98 бар.
174. 4.3. Температура и средняя кинетическая энергия теплового движения молекул
Из опыта известно, что если привести всоприкосновение два тела: горячее и холодное, то
через некоторое время их температуры
выровняются. Что перешло от одного тела к
другому?
Раньше, во времена Ломоносова и Лавуазье
считали, что носителем тепла является некоторая
жидкость – теплород.
На самом деле – ничего не переходит, только
изменяется средняя кинетическая энергия –
энергия движения молекул, из которых состоят эти
тела.
175. Величину T называют абсолютной темпе-ратурой и измеряют в градусах Кельвина (К). Она служит мерой кинетической энергии
Величину T называют абсолютной температурой и измеряют в градусах Кельвина (К). Онаслужит мерой кинетической энергии теплового
движения частиц идеального газа. Из (8.3.1)
получим:
m0 υ
2
2
3
kT .
2
Формула (8.3.2) применима для расчетов на
одну молекулу идеального газа.
Обозначим R kNA ,
где R – универсальная газовая постоянная:
Дж
Дж
3
R 8,31
8,31 10
моль K
кмоль К
176. В физике и технике за абсолютную шкалу температур принята шкала Кельвина, названная в честь знаменитого английского физика,
лорда Кельвина.1 К – одна из основных единиц системы СИ
Кроме того, используются и другие шкалы:
– шкала Фаренгейта (немецкий физик 1724 г.) –
точка таянья льда 32 F, точка кипения воды 212 F.
– шкала Цельсия (шведский физик 1842г.) – точка
таянья льда 0 С, точка кипения воды 100 С.
0 С = 273,15 К.
На рис.1.5приведено сравнение разных темп. шкал.
177. 4.4. Законы идеальных газов
В XVII – XIX веках былисформулированы опытные законы
идеальных газов, которые подробно
изучаются в школьном курсе физики.
Кратко напомним их.
Изопроцессы идеального газа –
процессы, при которых один из
параметров остаётся неизменным.
178. 1.Изохорический процесс. V = const. Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение
газа при этом изохорическомпроцессе подчиняется закону Шарля:
P/Т = const:
«При постоянном объёме и
неизменных значениях массы газа и его
молярной массы, отношение давления
газа к его абсолютной температуре
остаётся постоянным».
179. График изохорического процесса на РV диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ и VT
диаграммах:P1 P2
Уравнение изохоры:
.
T1 T2
180. 2. Изобарический процесс. Р = const. Изобарическим процессом называется процесс, протекающий при постоянном давлении Р.
Поведение газа при изобарическомпроцессе подчиняется закону ГейЛюссака:
V/T = const
«При постоянном давлении и
неизменных значениях массы газа и его
молярной массы, отношение объёма
газа к его абсолютной температуре
181. График изобарического процесса на VT диаграмме называется изобарой (рис. 4.8). Полезно знать графики изобарического процесса на
РV и РT диаграммах.Уравнение изобары
V1 V2
T1 T2
182. 3. Изотермический процесс. T = const. Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа приизотермическом процессе подчиняется
закону Бойля-Мариотта:
РV = const
«При постоянной температуре и
неизменных значениях массы газа и его
молярной массы, произведение объёма газа
на его давление остаётся постоянным».
График изотермического процесса на РV
– диаграмме называется изотермой.
183. Полезно знать графики изотермического процесса на VT и РT диаграммах (рис. 4.10).
Рисунок 4.10Уравнение изотермы
P1V1 P2V2 .
(4.4.5)
184. 4. Адиабатический процесс (изоэнтропийный (ΔS = 0, S = const)). Процесс, происходящий без теплообмена с окружающей средой.
Уравнение адиабаты:γ
V P const
где γ – показатель адиабаты.
На
рис.
показаны
графики
различных
изопроцессов в PVкоординатах.
Как
видно
из
рисунка,
адиабата
идет
круче, чем изотерма.
185.
6. Закон Авогадро.При одинаковых давлениях и
одинаковых температурах, в равных
объёмах различных идеальных газов
содержится одинаковое число молекул.
В одном моле различных веществ
содержится N A 6,022 10 23
молекул (число Авогадро).
Следствием этого закона является то, что моли
любых газов, при одинаковых температуре и
давлении, занимают одинаковые объемы. При
нормальных условиях объем моля равен:
Vμ = 22,41·10–3 м3/моль.
186. 7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов (Р1 – давление,
7. Закон Дальтона.Давление смеси идеальных газов
равно сумме парциальных давлений Р,
входящих в неё газов
Pсм P1 P2 ... Pn
(Р1 – давление, которое оказывал бы определённый
газ из смеси, если бы он занимал весь объём).
m1RT m2 RT RT m1 m2
Pñì
.
μ1V
μ 2V
V μ1 μ 2
187. 8. Объединённый газовый закон (Закон Клапейрона). В соответствии с законами Бойля - Мариотта (4.4.5) и Гей-Люссака (4.4.3)
можно сделатьзаключение, что для данной массы газа
P1V1 P2V2
или
T1
T2
PV
const.
T
(4.4.7)
Это объединённый газовый закон
Клапейрона.
188. Клапейрон Бенуа Поль Эмиль (1799 – 1864) – французский физик и инженер. Физические исследования посвящены теплоте, пластичности
иравновесию твердых тел. Придал
математическую форму идеям Н. Карно,
первым оценил большое научное
значение его труда. Вывел уравнения
состояния идеального газа. Впервые ввел
в термодинамику графический метод.
189. 4.5. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Идеальным газом называют газ, молекулыкоторого пренебрежимо малы, по сравнению
расстояния между ними, и не взаимодействуют
друг с другом на расстоянии.
Все газы, при нормальных условиях, близки
по свойствам к идеальному газу. Ближе всех
газов к идеальному газу – водород.
Уравнение,
связывающее
основные
параметры состояния идеального газа вывел
великий русский ученый Д.И. Менделеев.
190. Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и Шарля с законом Авогадро. Уравнение, связывающее все эти
законы, называетсяуравнением Менделеева-Клапейрона и
записывается так:
m
PV RT ,
μ
(4.5.1)
m
здесь μ – число молей. Для одного моля
можно записать PVμ RT
191. Если обозначим – плотность газа, то (4.5.2) Если рассматривать смесь газов, заполняющих объём V при температуре Т, тогда,
mρ
Если обозначим V
– плотность газа, то
m
ρ
P
RT RT .
μV
μ
(4.5.2)
Если рассматривать смесь газов,
заполняющих объём V при температуре Т,
тогда, парциальные давления, можно найти,
как:
m1RT
P1
,
μ1V
m2 RT
mn RT
P2
, ….. Pn
μ nV
μ 2V
192. Согласно закону Дальтона: полное давление смеси газа равно сумме парциальных давлений всех газов, входящих в смесь Отсюда, с
Согласно закону Дальтона: полное давлениесмеси газа равно сумме парциальных
давлений всех газов, входящих в смесь
P P1 P2 ... Pn
Отсюда, с учетом вышеизложенного, можно
записать
m1 m2
mn
PV
... RT (4.5.3)
μn
μ1 μ 2
– это уравнение Менделеева-Клапейрона
для смеси газов.
193. 4.6. Явления переноса в газах
Из прошлых лекций мы знаем, чтомолекулы в газе движутся со скоростью
звука, с такой же скоростью движется пуля.
Однако, находясь в противоположном
конце комнаты, запах разлитой пахучей
жидкости
мы
почувствуем
через
сравнительно
большой
промежуток
времени. Это происходит потому, что
молекулы
движутся
хаотически,
сталкиваются друг с другом, траектория
движения у них ломанная.
194. Рассмотрим некоторые явления, происходящие в газах. Распространение молекул примеси в газе от источника называется диффузией. В
состоянии равновесия температура Т иконцентрация n во всех точках системы
одинакова. При отклонении плотности от
равновесного значения в некоторой части
системы возникает движение компонент
вещества в направлениях, приводящих к
выравниванию концентрации по всему
объему системы.
195. Связанный с этим движением перенос вещества обусловлен диффузией. Диффузионный поток будет пропорционален градиенту
концентрации:dn
J~
dx
196. Если какое либо тело движется в газе, то оно сталкивается с молекулами газа и сообщает им импульс. С другой стороны, тело тоже
будет испытывать соударения состороны молекул, и получать собственный
импульс, но направленный в противоположную сторону. Газ ускоряется, тело
тормозиться, то есть, на тело действуют
силы трения. Такая же сила трения будет
действовать и между двумя соседними
слоями газа, движущимися с разными
скоростями.
197. Это явление носит название внутреннее трение или вязкость газа, причём сила трения пропорциональна градиенту скорости: (4.6.1)
Это явление носит название внутреннеетрение или вязкость газа, причём сила
трения
пропорциональна
градиенту
скорости:
dυ
Fтр ~
dx
(4.6.1)
198. Если в соседних слоях газа создана и поддерживается разность температур, то между ними будет происходить обмен тепла. Благодаря
хаотическомудвижению, молекулы в соседних слоях
будут перемешиваться и, их средние
энергии будут выравниваться.
Происходит перенос энергии от более
нагретых слоев к более холодным.
199. называется теплопроводностью. Поток тепла пропорционален градиенту температуры:
Перенос энергии от более нагретыхслоев к более холодным
называется теплопроводностью.
Поток тепла пропорционален
градиенту температуры:
dT
Q~
dx
(4.6.2)
200. В процессе диффузии, при тепло- и электропроводности происходит перенос вещества, а при внутреннем трении – перенос энергии. В
основе этих явлений лежит один и тотже механизм – хаотическое движение
молекул. Общность механизма,
обуславливающего все эти явления переноса,
приводит к тому, что их закономерности
должны быть похожи друг на друга.
201. 4.8. Диффузия газов
Диффузия от латинского diffusio –распространение, растекание взаимное
проникновение соприкасающихся веществ
друг в друга, вследствие теплового
движения частиц вещества.
Диффузия происходит в направлении
уменьшения концентрации вещества и ведет
к его равномерному распределению по
занимаемому объему.
202. Диффузия имеет место в газах, жидкостях и твердых телах. Наиболее быстро диффузия происходит в газах, медленнее в жидкостях,
ещемедленнее в твердых телах, что обусловлено
характером движения частиц в этих средах.
Для газа диффузия – это распределение
молекул примеси от источника
(или взаимная диффузия газа).
203. Обозначим: – коэффициент диффузии. Тогда диффузионный поток будет равен: (4.7.2) или в общем случае (в трёхмерной системе)
1Обозначим: D λ υ – коэффициент
3
диффузии.
Тогда диффузионный поток будет равен:
dn
J D ,
dx
(4.7.2)
или в общем случае (в трёхмерной системе)
J D grad n
– уравнение Фика.
(4.7.3)
204. Из уравнения Фика видно, что диффузионный поток, направлен в сторону уменьшения концентрации. При этом коэффициент диффузии D
J D grad nИз уравнения Фика видно, что
диффузионный поток, направлен в сторону
уменьшения концентрации.
При этом коэффициент диффузии D
численно равен диффузионному потоку
через единицу площади в единицу времени
при grad n 1
Измеряется коэффициент диффузии D
в м/с2.
205. 4.9. Внутреннее трение. Вязкость газов
Рассмотрим ещё одну систему координат: υот х
(рисунок 4.5)
206. Пусть в покоящемся газе вверх, перпендикулярно оси х движется пластинка со скоростью υ0, причём (υT – скорость теплового
Пусть в покоящемся газе вверх,перпендикулярно оси х движется пластинка
со скоростью υ0, причём υ0 υT
(υT – скорость теплового движения молекул).
Пластинка увлекает за собой
прилегающий слой газа, тот слой – соседний
и так далее. Весь газ делится, как бы на
тончайшие слои, скользящие вверх тем
медленнее, чем дальше они от пластинки.
Раз слои газа движутся с разными
скоростями, возникает трение.
Выясним причину трения в газе.
207. Сила, действующая на единицу площади поверхности, разделяющей два соседних слоя газа: Или, в общем виде Это уравнение Ньютона.
Сила, действующая на единицу площадиповерхности, разделяющей два соседних
dυ
слоя газа:
f η
dx
.
f η grad υ.
Или, в общем виде
Это уравнение Ньютона.
Здесь η – коэффициент вязкости:
1
η λ υ nm0 Dρ, (4.7.3)
3
где D – коэффициент диффузии; ρ – плотность газа
208. Физический смысл коэффициента вязкости η в том, что он численно равен импульсу, переносимому в единицу времени через единицу
1η λ υ nm0 Dρ,
3
Физический смысл коэффициента
вязкости η в том, что он численно равен
импульсу, переносимому в единицу времени
через единицу площади при градиенте
скорости равном единице.
209. 4.10. Теплопроводность газов
Учение о теплопроводностиначало развиваться в XVIII в. и
получило свое завершение в
работах французского ученого Ж.
Фурье (1786 – 1830),
опубликовавшего в 1822 г. книгу
«Аналитическая теория теплоты».
210. или (4.10.1) – уравнение теплопроводности Ж.Фурье. Здесь q – тепловой поток; χ – коэффициент теплопроводности, равный: или
илиq χ grad T
(4.10.1)
– уравнение теплопроводности Ж.Фурье.
Здесь q – тепловой поток;
χ – коэффициент теплопроводности,
равный:
1
i
χ λ υT n k
3
2
1
χ λ υT ρCVУД
3
или
(4.10.2)
(4.10.3)
211. υТ – тепловая скорость молекул; – удельная теплоемкость при постоянном объеме. Найдем размерность коэффициента
1χ λ υT ρCVУД
3
υТ – тепловая скорость молекул;
CVуд– удельная теплоемкость при
постоянном объеме.
Найдем размерность коэффициента
теплопроводности:
qdx
Дж м
кг м
χ
2
3
dT м К с с К
212. 4.11. Уравнения и коэффициенты переноса
Сопоставим уравнения переносаJ Dgrad n
dn
J D
dx
Уравнение Фика для диффузии.
Коэффициент диффузии
1
D λ υT
3
213.
f тр η grad υdυ
или f
Уравнение Ньютона
η
тр
dx
для трения.
Коэффициент вязкости:
1
η λ υT nm0 Dρ.
3
214. 4.12. Внутренняя энергия. Работа и теплота
Наряду с механической энергией любое тело(или система) обладает внутренней энергией.
Внутренняя энергия – энергия покоя.
Она складывается из:
1. теплового хаотического
движения молекул,
2. потенциальной энергии их
взаимного
расположения,
3. кинетической и потенциальной энергии
электронов в атомах, нуклонов в ядрах и т. д.
215. В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы
В термодинамике важно знать неабсолютное значение внутренней энергии,
а её изменение.
В
термодинамических
процессах
изменяется только кинетическая энергия
движущихся молекул (тепловой энергии
недостаточно, чтобы изменить строение
атома,
а
тем
более
ядра).
Следовательно, фактически под
внутренней энергией в термодинамике
подразумевают энергию теплового
хаотического движения молекул.
216. Внутренняя энергия U одного моля идеального газа равна: или Таким образом, внутренняя энергия зависит только от температуры.
Внутренняя энергия U одного моляидеального газа равна:
3
3
U N A K kTN A RT , или
2
2
3
U RT
2
Таким образом, внутренняя энергия зависит
только от температуры.
Внутренняя энергия U является функцией
состояния системы независимо от предыстории
217. Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы: – это и есть первое
Количество теплоты, сообщаемой телу,идёт на увеличение внутренней энергии и
на совершение телом работы:
Q ΔU A
– это и есть первое начало
термодинамики или закон сохранения
энергии в термодинамике.
218.
219. Правило знаков: если тепло передаётся от окружающей среды данной системе, при этом Если система производит работу над
Правило знаков: ΔQ 0, если тепло передаётсяот окружающей среды данной системе, при этом
ΔU 0
ΔA 0,
Если система производит работу над
окружающими телами, то: U 0
Учитывая правило знаков, первое начало
термодинамики можно записать в виде:
ΔU Q A
– изменение внутренней энергии тела
равно разности сообщаемой телу
теплоты и произведённой телом работы.
220. Закон сохранения энергии для малого изменения состояния системы будет иметь вид: U – функция состояния системы; dU – её полный
Закон сохранения энергии длямалого изменения состояния системы
будет иметь вид:
Q dU A.
U – функция состояния системы;
dU – её полный дифференциал, а
δQ и δА не являются функциями
состояния.
221. Теплота Q и работа А зависят от того, каким образом совершен переход из состояния 1 в состояние 2 (изохорически,
адиабатически), а внутренняя энергия U независит.
При этом нельзя сказать, что система,
обладает определенным для данного
состояния значением теплоты и работы.
Количество теплоты Q выражается в тех
же единицах, что работа и энергия, т.е. в
джоулях [Q] = Дж.
222. Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя ряд состояний,
возвращается в исходное.δQ dU δA.
223. первое начало термодинамики не указывает, в каком направлении идут процессы изменения состояния.
Недостатки первого начала :первое начало термодинамики
не указывает, в каком направлении
идут
процессы
изменения
состояния.
224. Числом степени свободы называется число независимых переменных, определяющих положение тела в пространстве и обознача-ется i i
Числом степени свободы называется числонезависимых переменных, определяющих
положение тела в пространстве и обозначается i
i=3
Как видно, положение материальной
точки (одноатомной молекулы) задаётся
тремя координатами, поэтому она имеет
три степени свободы: i = 3
225.
У двухатомных молекул пять степеней свободыi = 5,
у трёхатомных шесть степеней свободы
i = 6.
i=3
i=5
i=6
226. Больцман доказал, что, средняя энергия приходящаяся на одну степень свободы равна
Закон о равномерном распределенииэнергии по
степеням свободы
Больцман доказал, что, средняя
энергия
K
приходящаяся на одну степень
свободы равна
1
kT .
2
227.
Итак, средняя энергия приходящаяся наодну степень свободы:
1
K kT .
2
(4.4.1)
228. У одноатомной молекулы i = 3, тогда для двухатомных молекул i = 5 для трёхатомных молекул i = 6
У одноатомной молекулы i = 3, тогда3
K kT ,
2
для двухатомных молекул i = 5
5
K kT ,
2
для трёхатомных молекул i = 6
6
K kT .
2
229. На среднюю кинетическую энергию молекулы, имеющей i-степеней свободы приходится (4.4.5) Это и есть закон Больцмана о
На среднюю кинетическую энергиюмолекулы, имеющей i-степеней свободы
приходится
i
K kT
2
Это и есть закон Больцмана о
равномерном распределении средней
кинетической энергии по степеням
свободы.
Здесь
(4.4.6)
i = 3iп + iвр + 2iкол
(4.4.5)
230.
i iпост iв ращ 2iколеб231. Для произвольного количества газов: , (4.4.9) (4.4.10) Из теории также следует, что СV не зависит от температуры (рис.).
Для произвольного количества газов:mi
CV
R
μ2
,
mi 2
CP
R.
μ 2
Из теории также следует, что СV не
зависит от температуры (рис.).
(4.4.9)
(4.4.10)
232. 4.13. Применение первого начала термодинамики к изопроцессам идеальных газов
В таблице приводятся сводные данные охарактеристиках изопроцессов в газах.
Изопроцессы
–
процессы,
при
которых
один
из
термодинамических параметров остается постоянным
Здесь используются известные нам формулы:
δQ dU δA – I начало термодинамики
или
закон
сохранения
энергии
в
термодинамике:
233.
Название процессаИзохорический
Условие
протекания
процесса
V = const
Изобарический
Изотермический
P = const
T = const
Закон
Закон Шарля
Гей-Люссака
Связь между
параметрами
состояния
P
const
T
Первое
начало ТД
δQ dU
PV const
m
RdT
μ
Работа в
процессе
A 0
δQ dU δA δQ δA
TV γ 1 const
dU δA
δA = PdV = dU
δA PdV
m
A RΔT
μ
A
V2
A PdV
V1
A P(V V ) A
2
CP i 2
CV
i
T γ P γ 1 const
δA PdV
δA 0
γ
PV γ const
V
const
T
PdV
Закон Бойля –
Мариотта
Адиабатический
δQ = 0
1
А = −∆U = – CVΔТ
m
V
RT ln 2 δA m i RdT
μ
V1
μ 2
m
Р
RT ln 1
μ
Р2
γ 1
P1V1 V1
1
A
γ 1 V2
234.
Количествотеплоты,
сообщённое в
процессе
δQ dU
δQ CV dT
Q CV ΔТ
dU = δQ
Изменение
внутренней
энергии
i
ΔU VΔP
2
Теплоёмкость
Q = СP (T2 T1)
Q
m i
1 R ΔT
μ 2
dU = СV dT
U = СV (T2 T1)
i
ΔU PΔV
2
V
ΔР
γ 1
mi
ΔU
RΔT
μ 2
dU i
R
dT 2
CP
ΔU
CV
δQ = СP dT
δQ = δA
Q=A
δQ = 0
Q=0
dU = δA
dU = 0
U = –A = –СV ΔT
P1V1
ΔU
T1 ( γ 1)
m γR
μ ( γ 1)
m R
CV
μ ( γ 1) C dQ i 1 R
P
dT 2
CТ =
Сад = 0


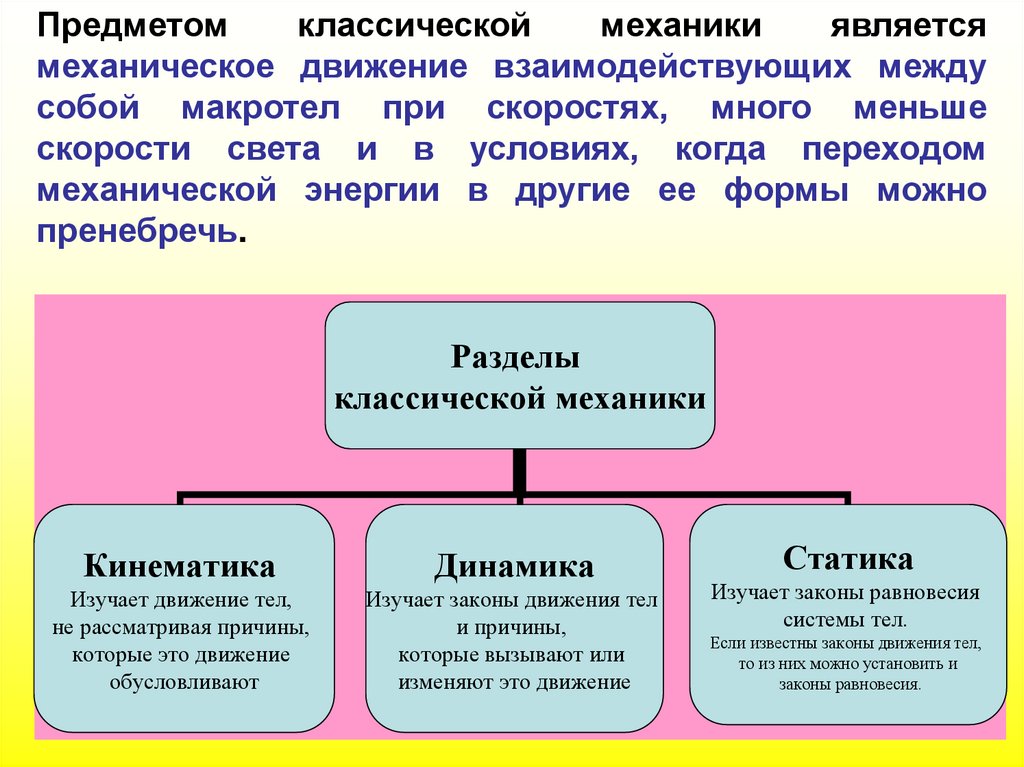




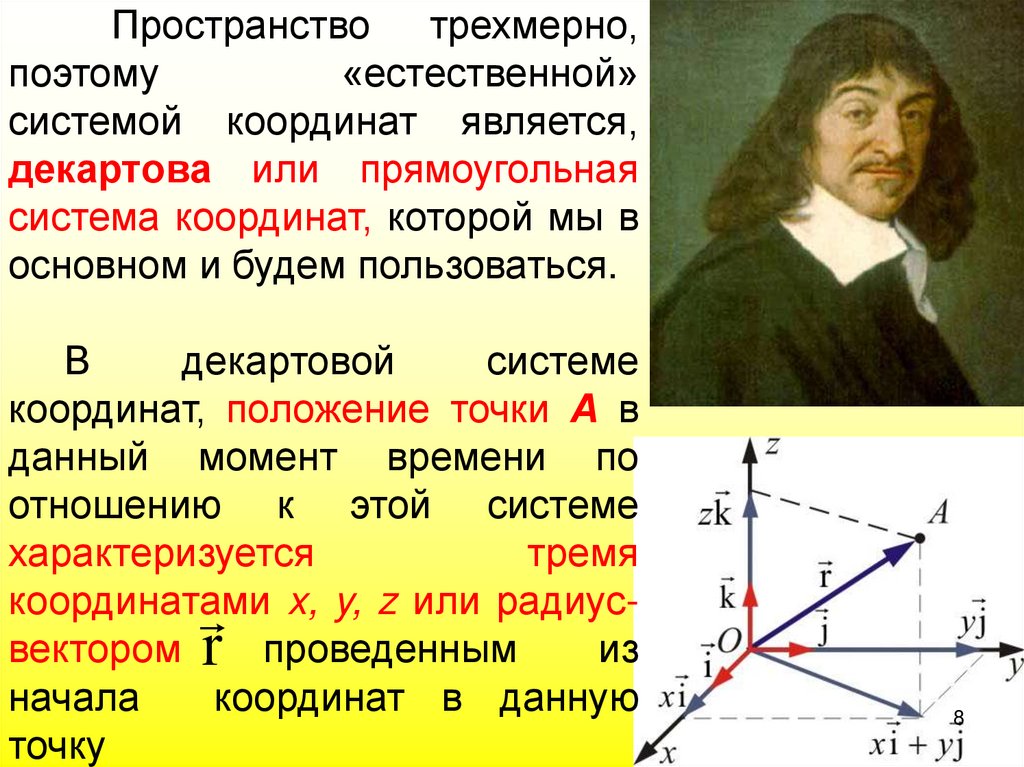
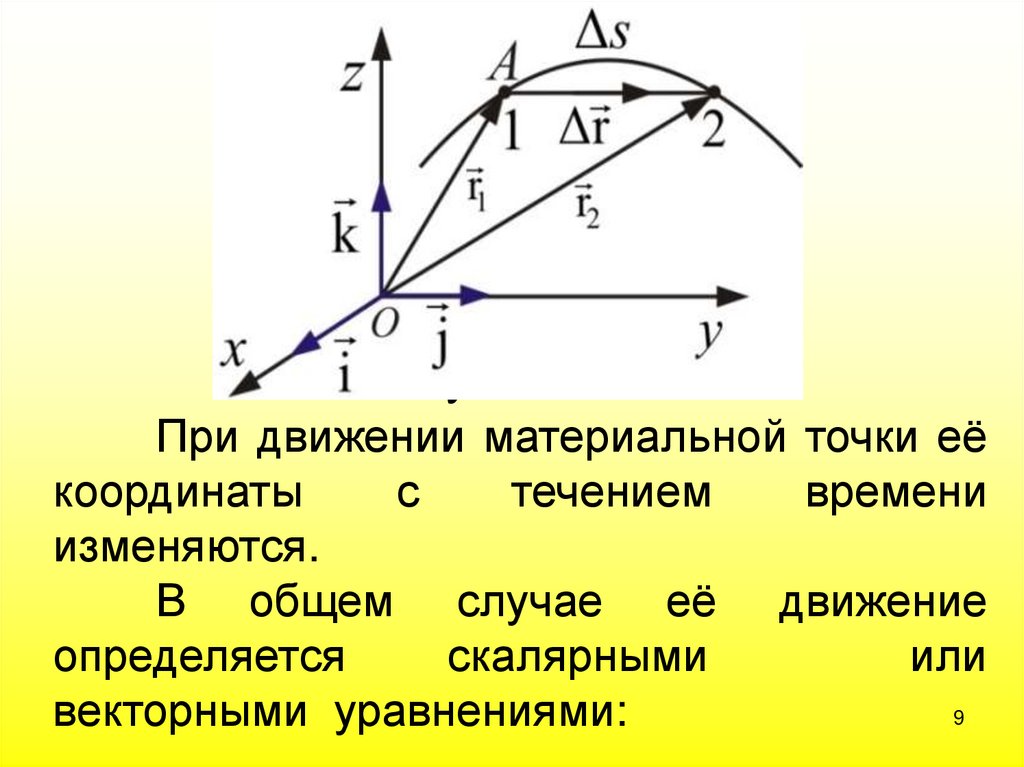


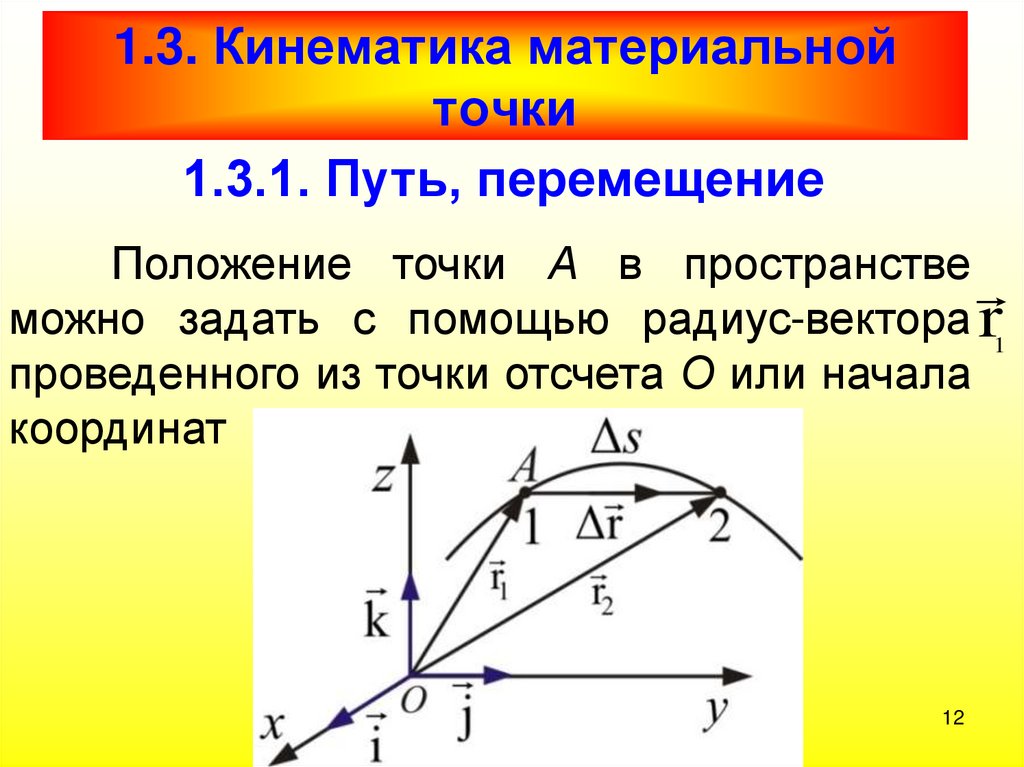


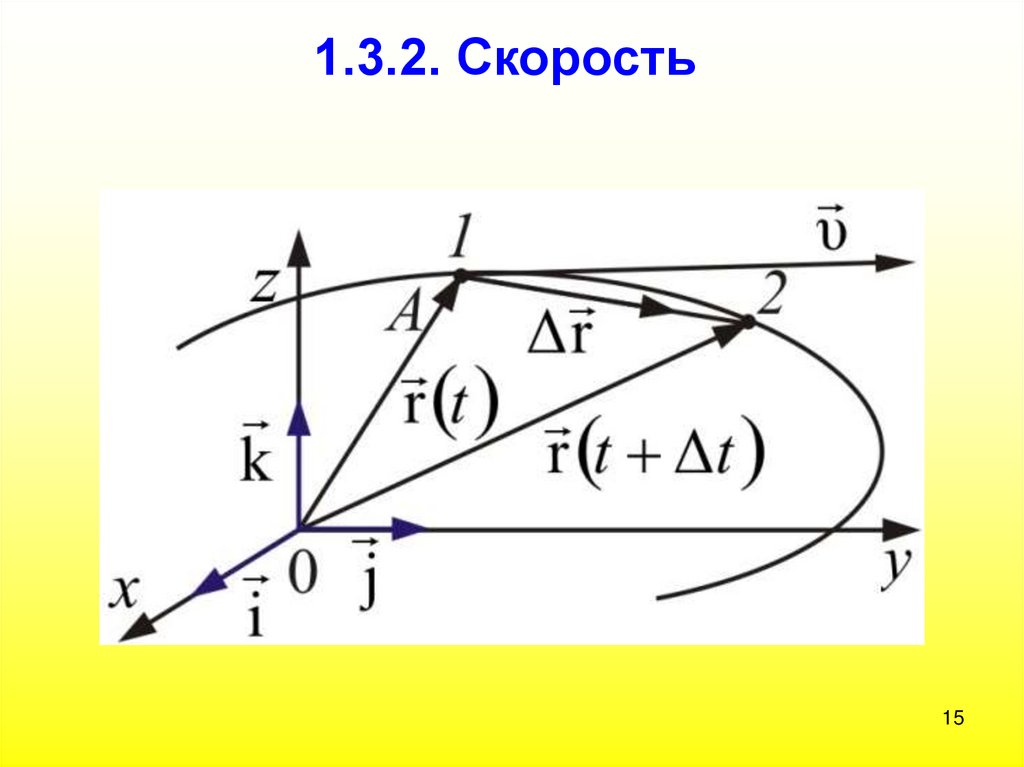
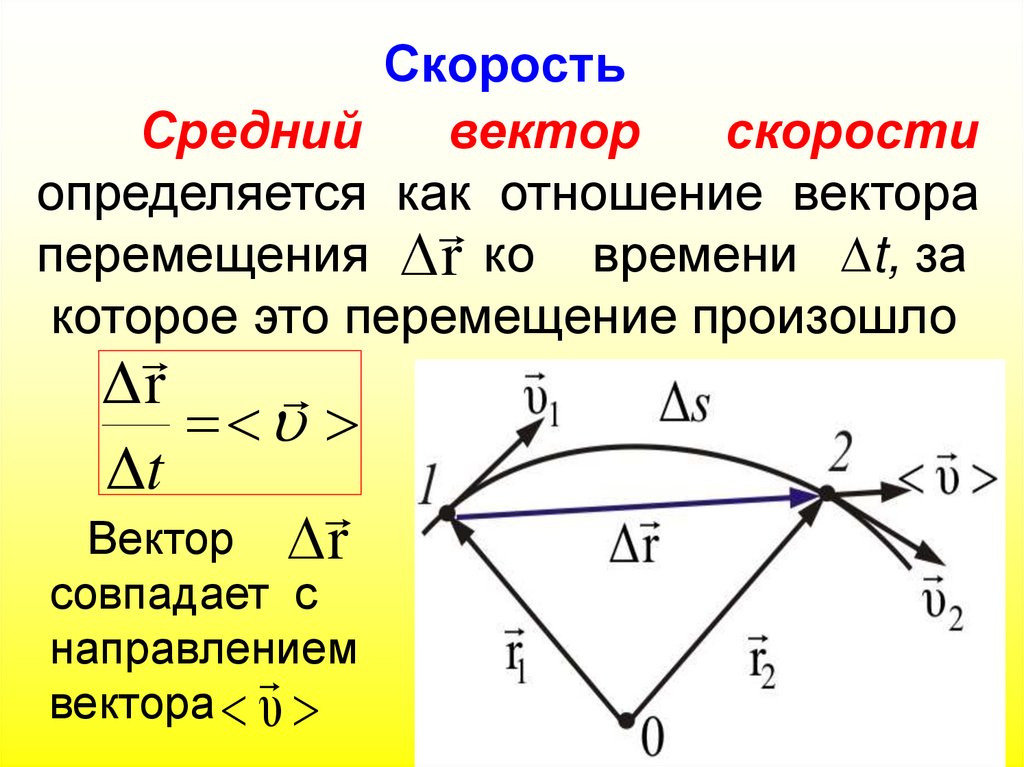
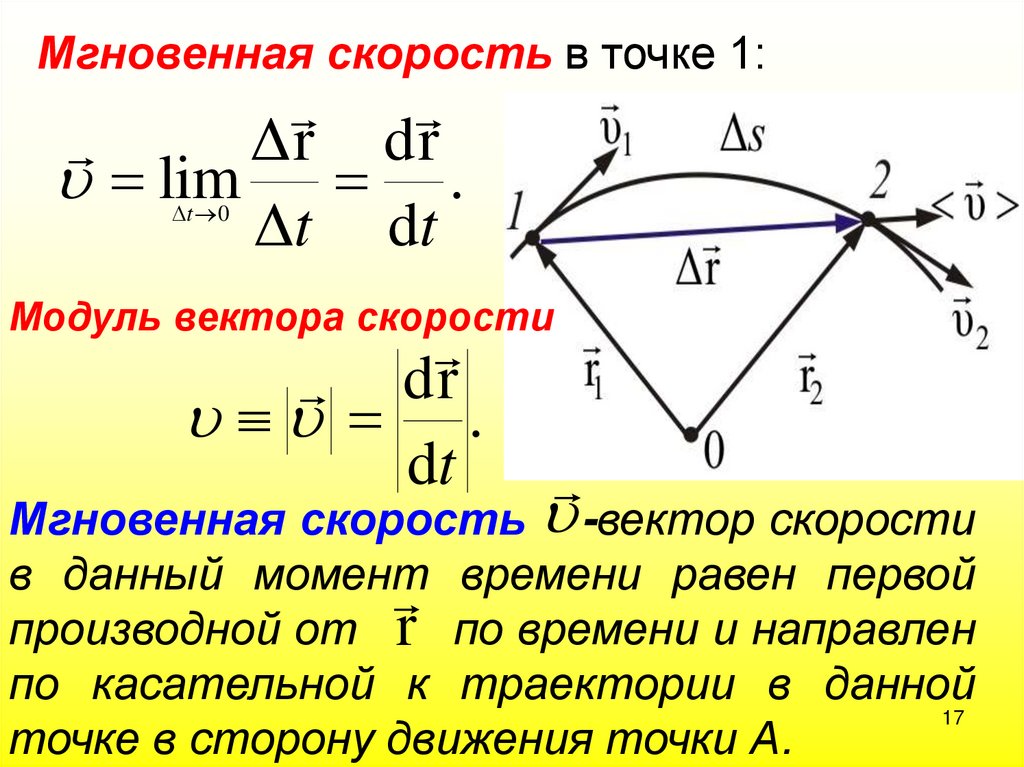
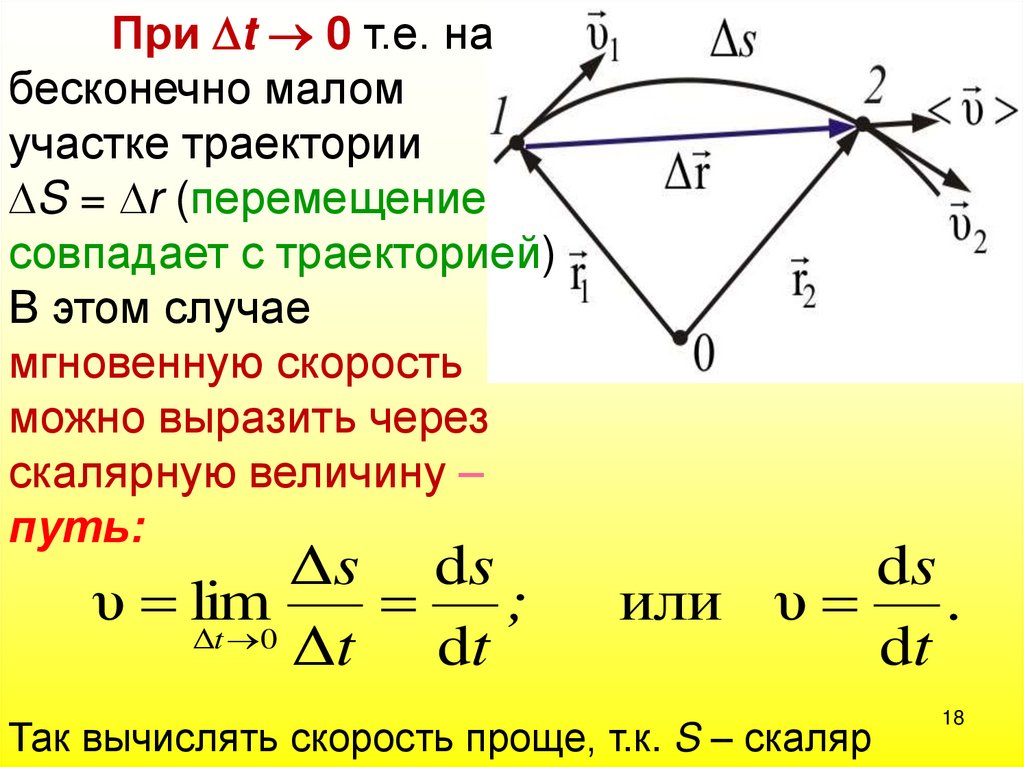


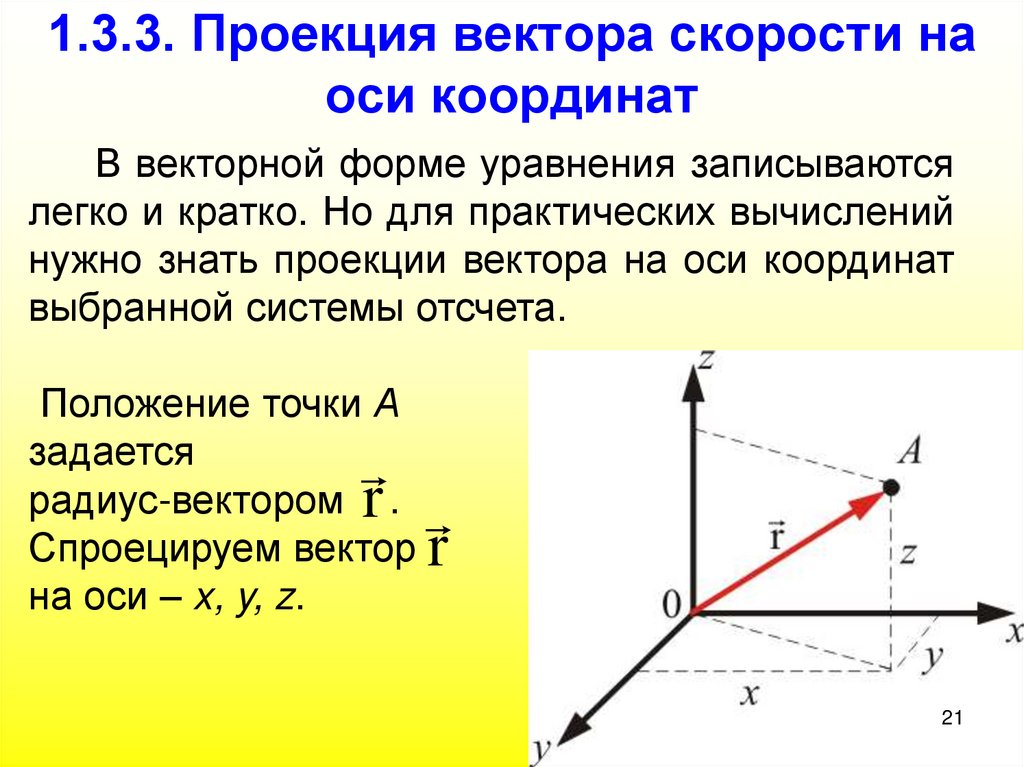

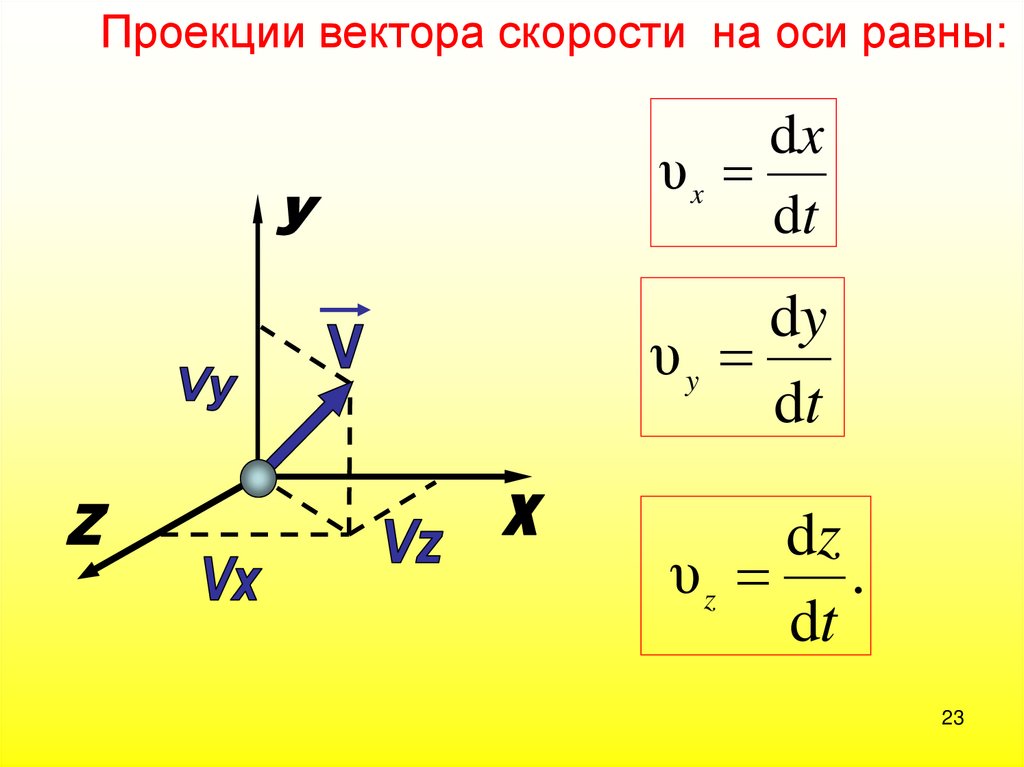






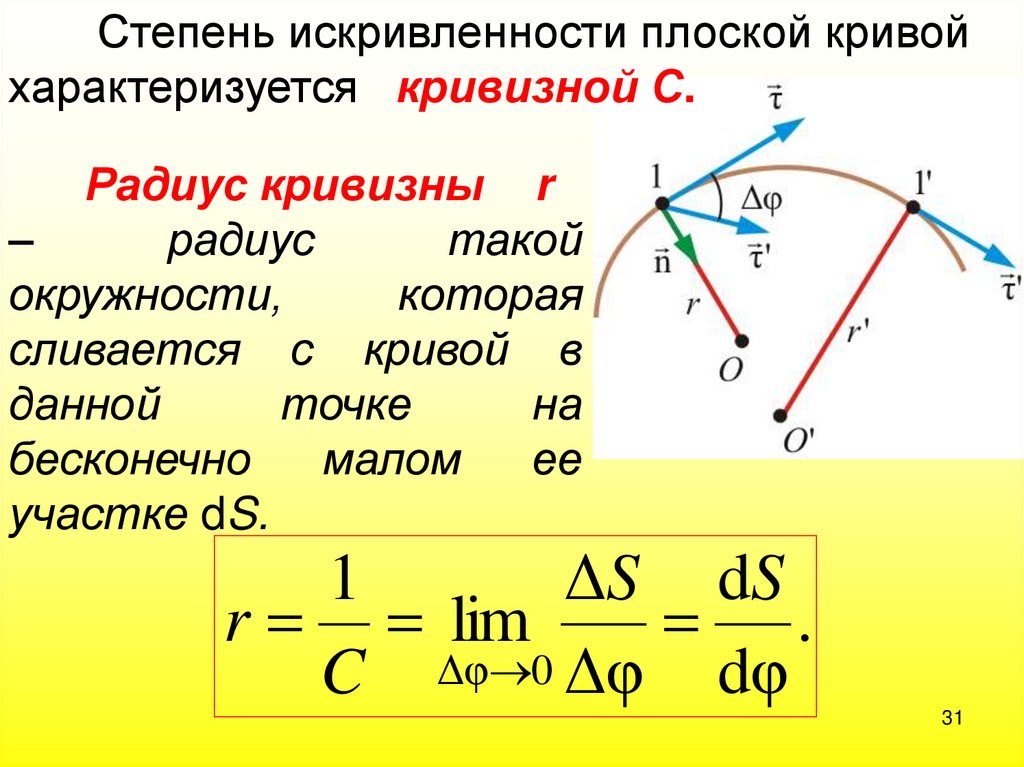

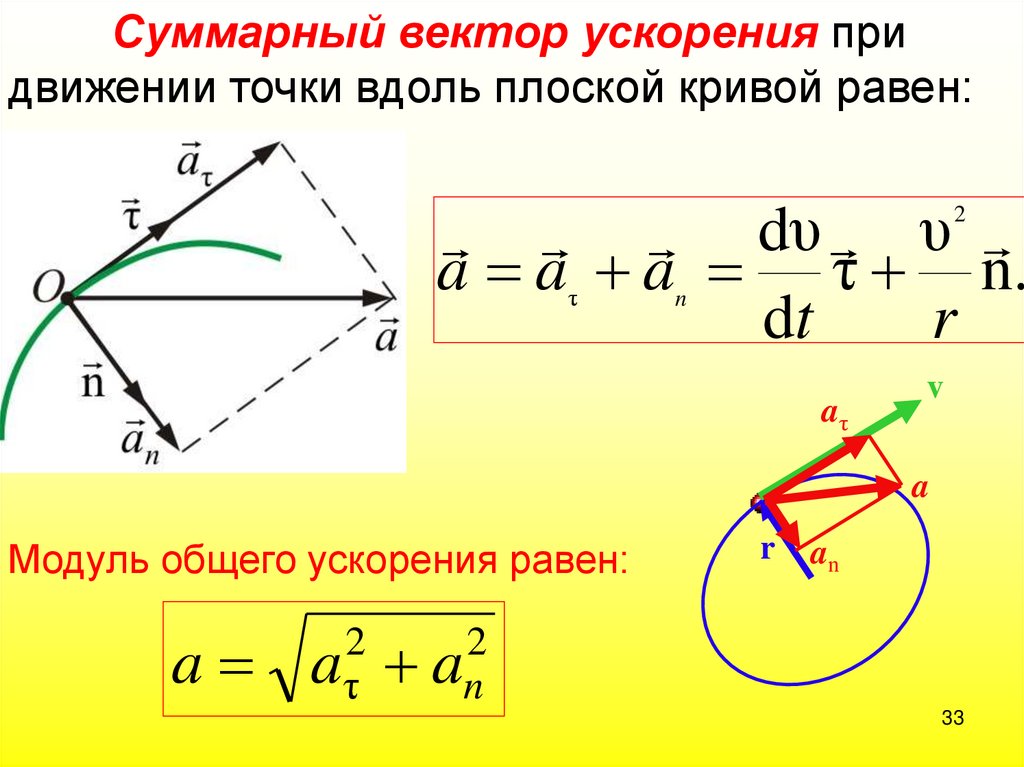





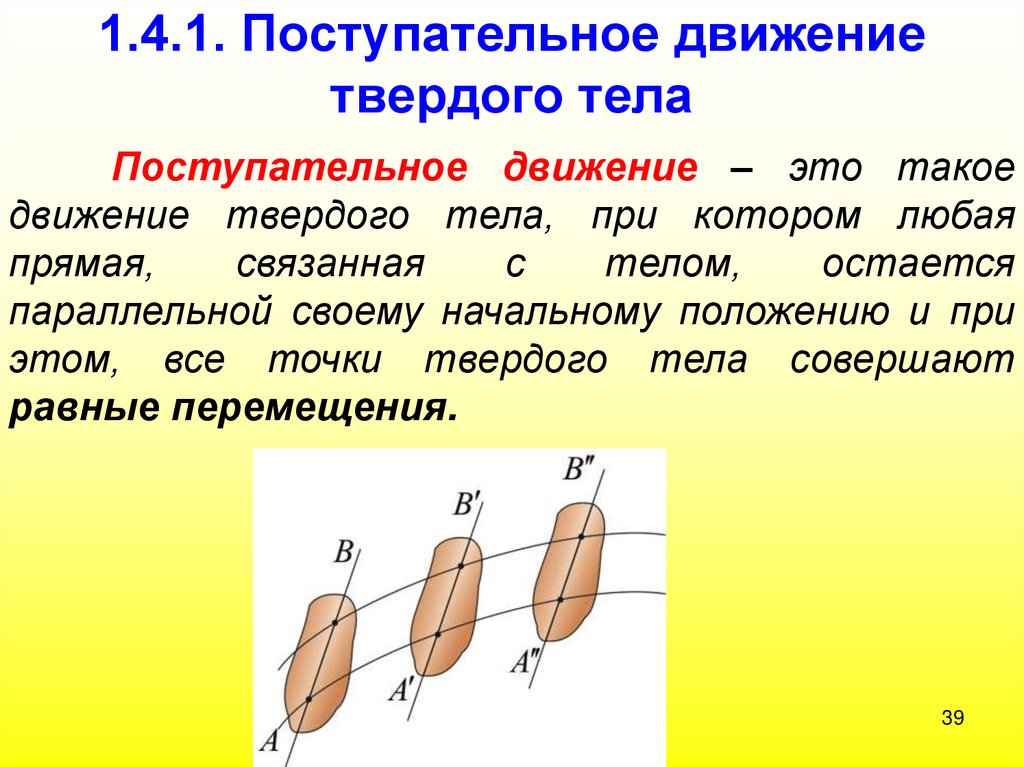
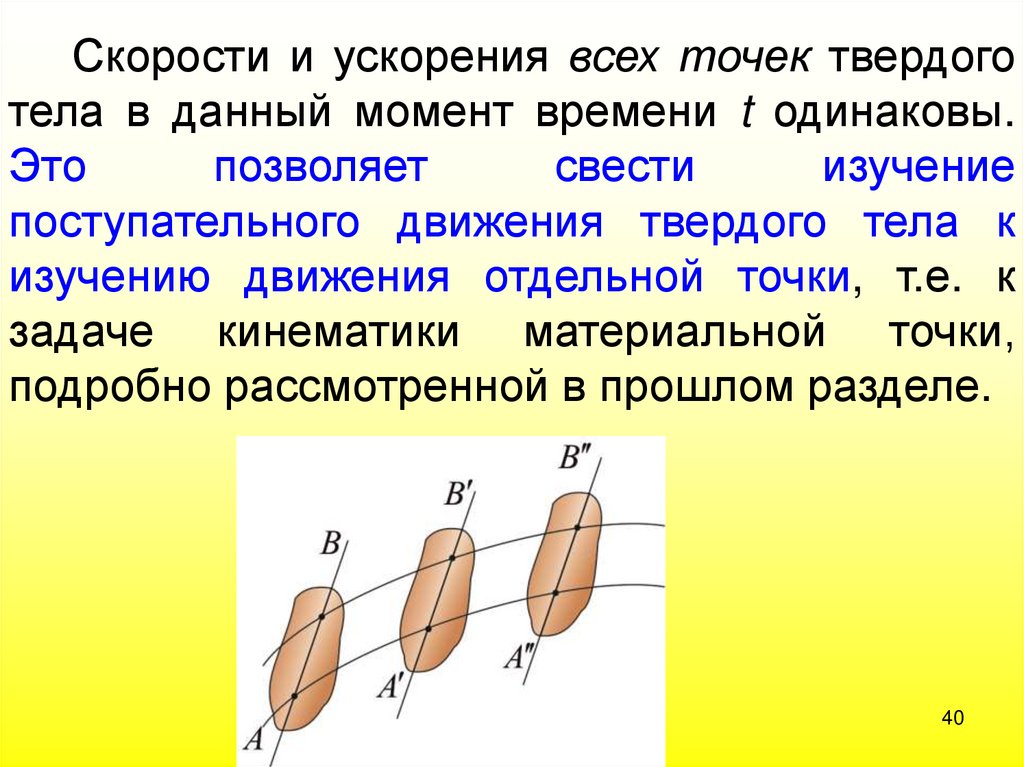
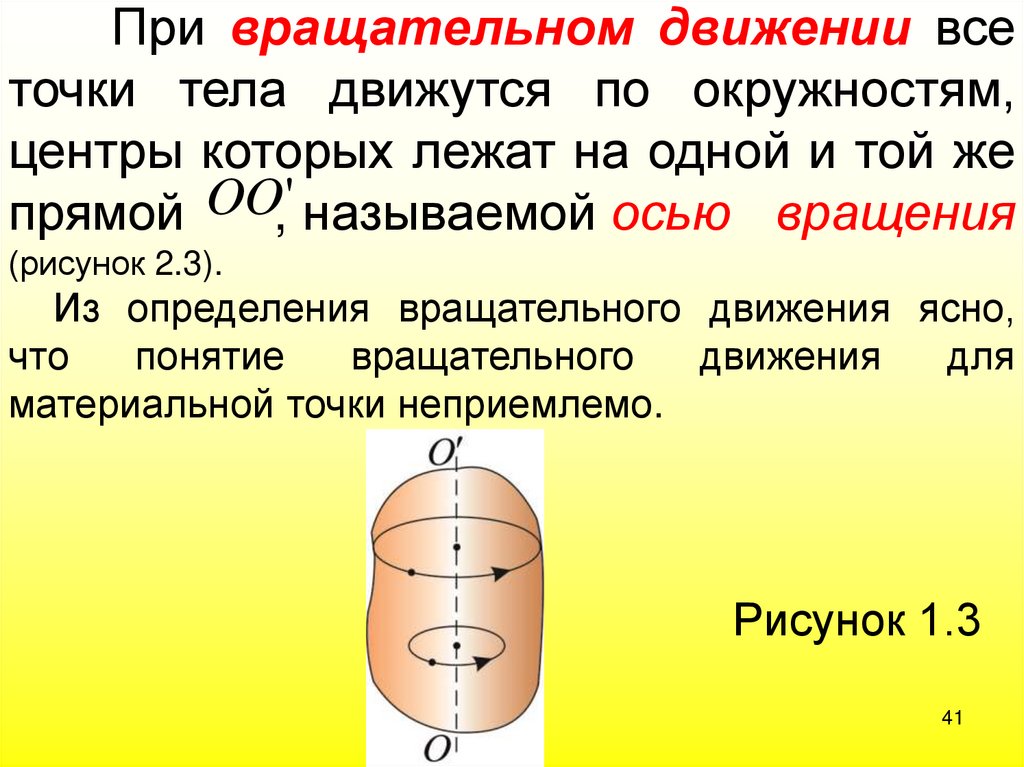

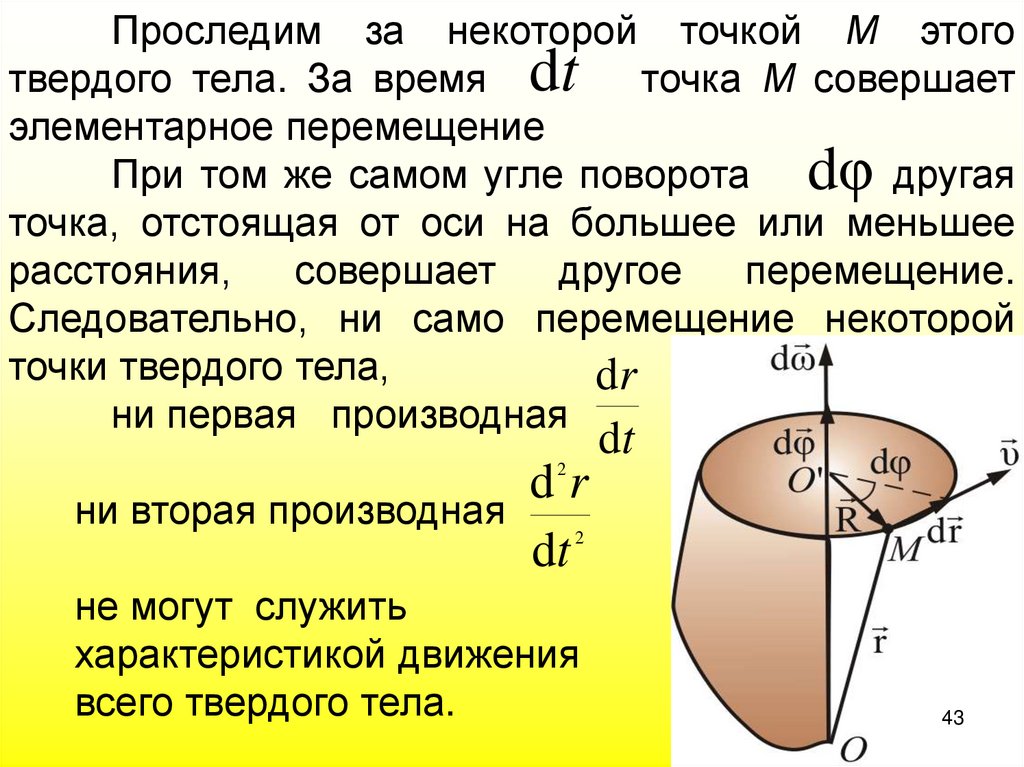
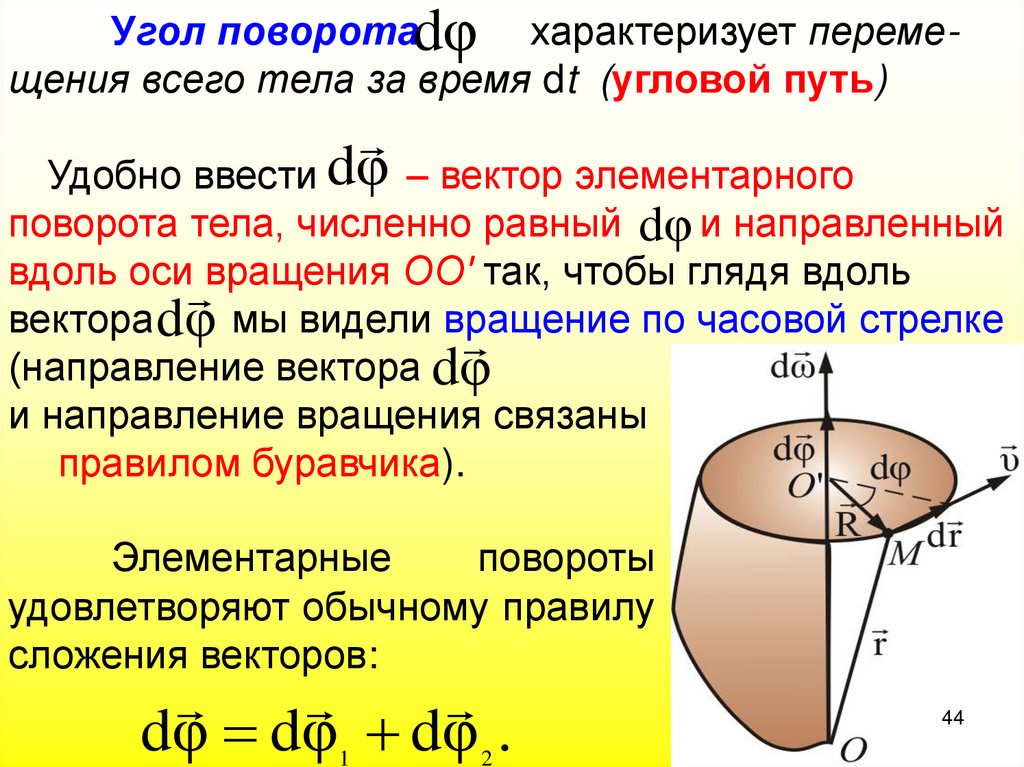
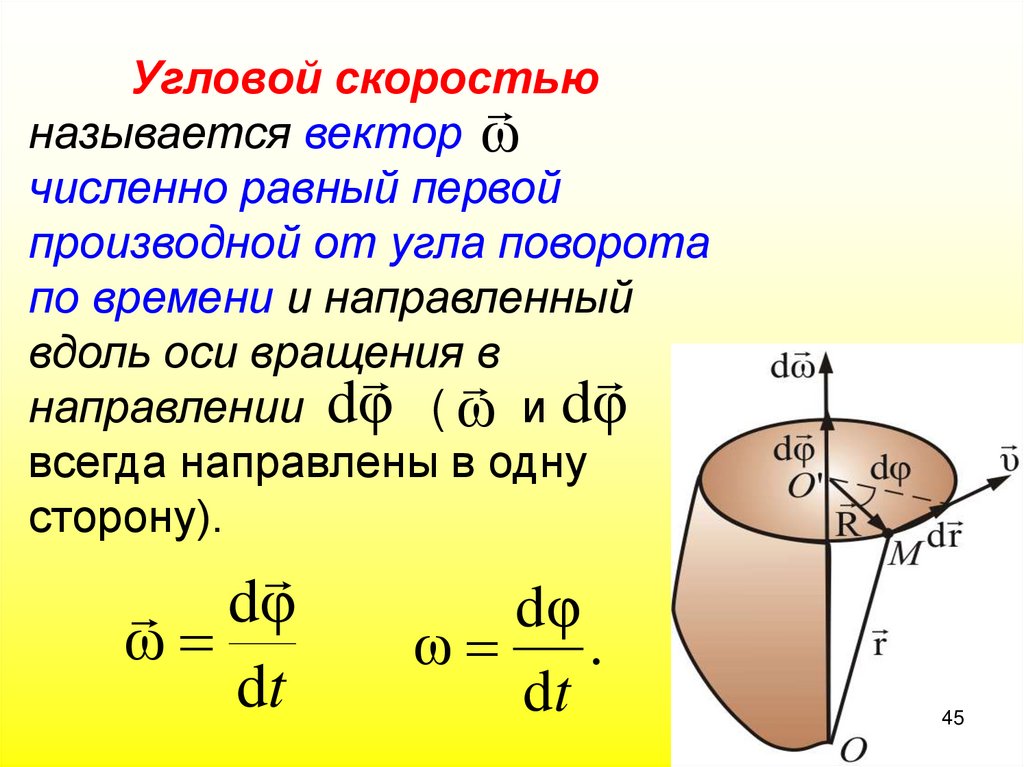
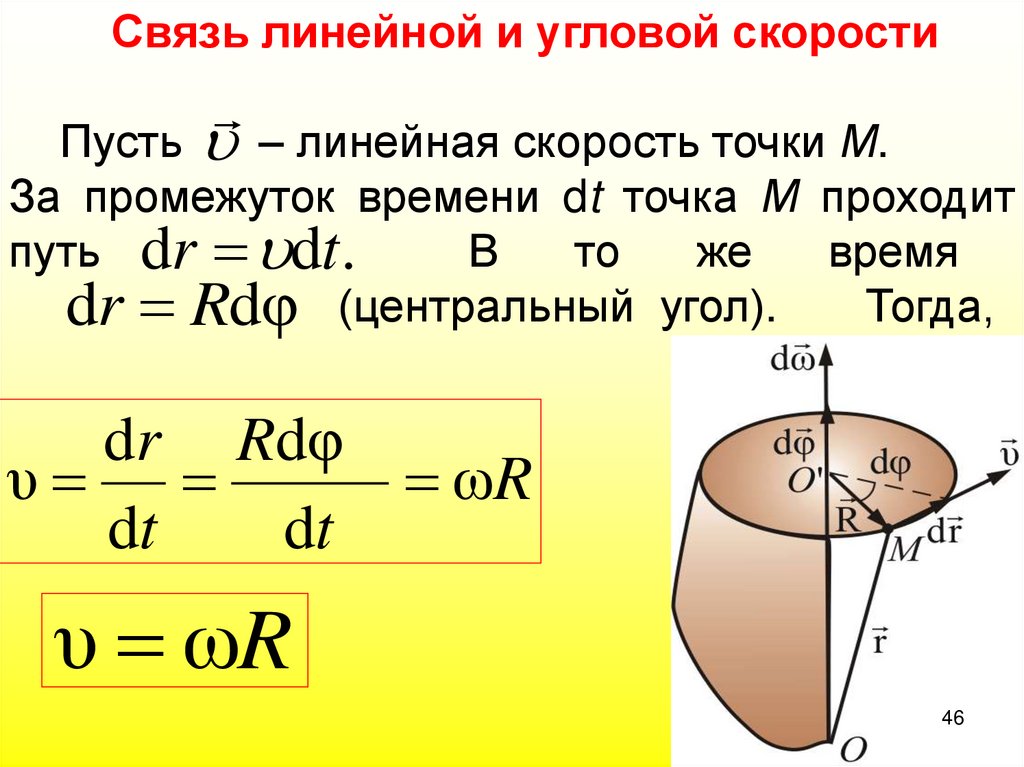
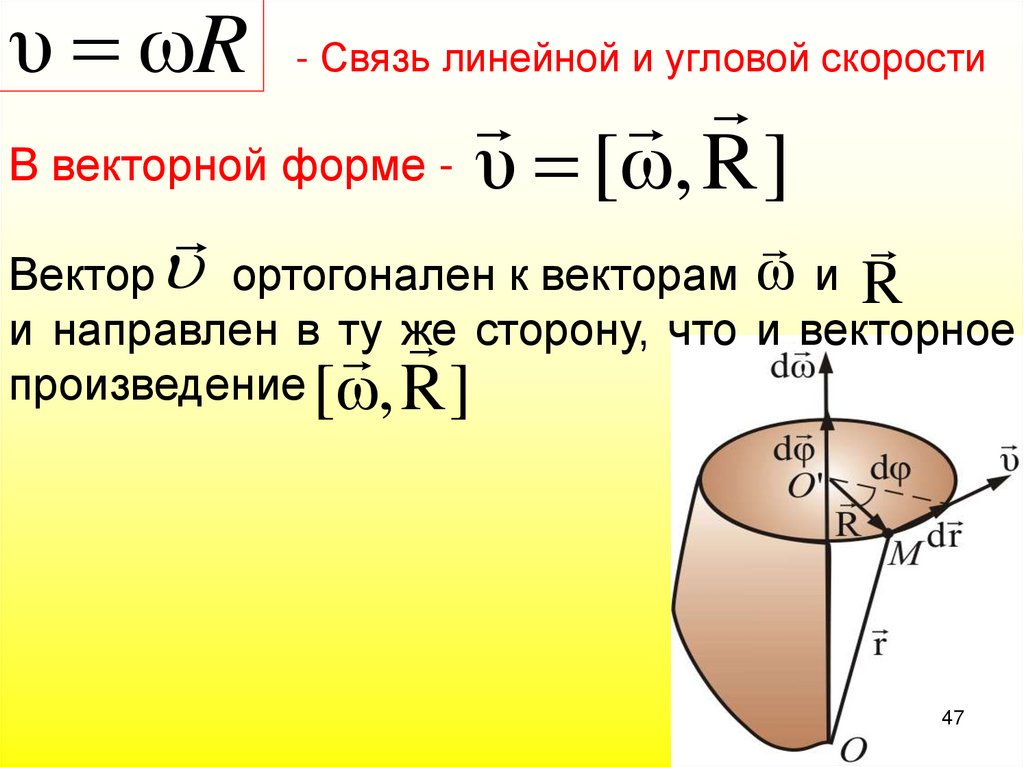

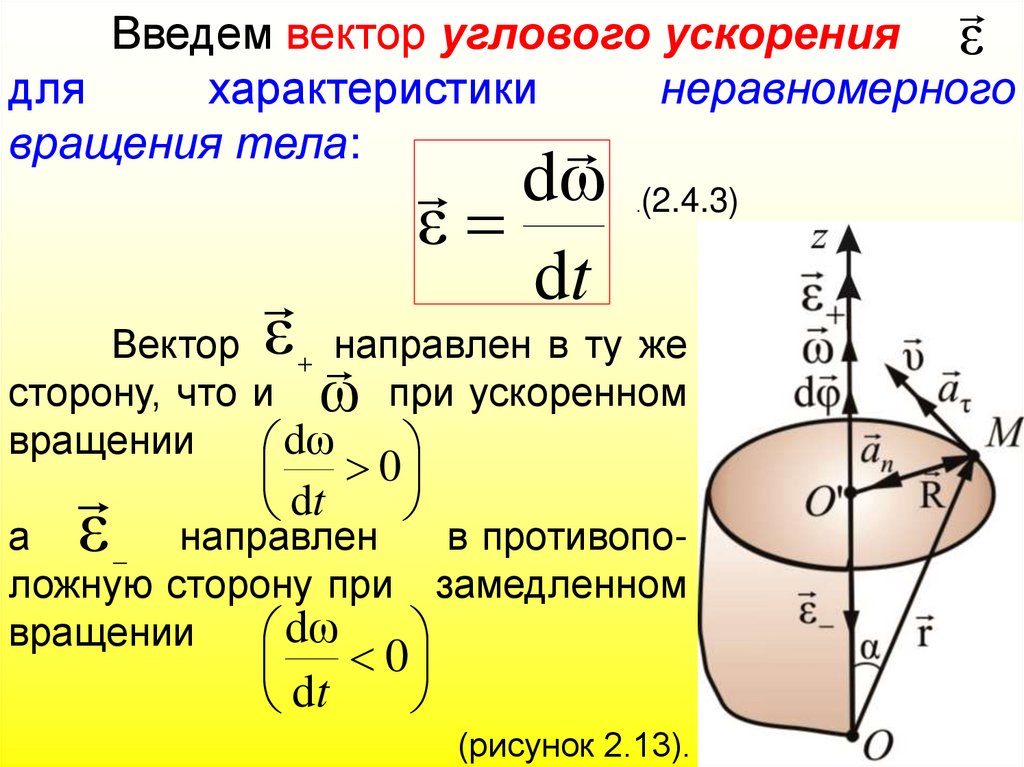
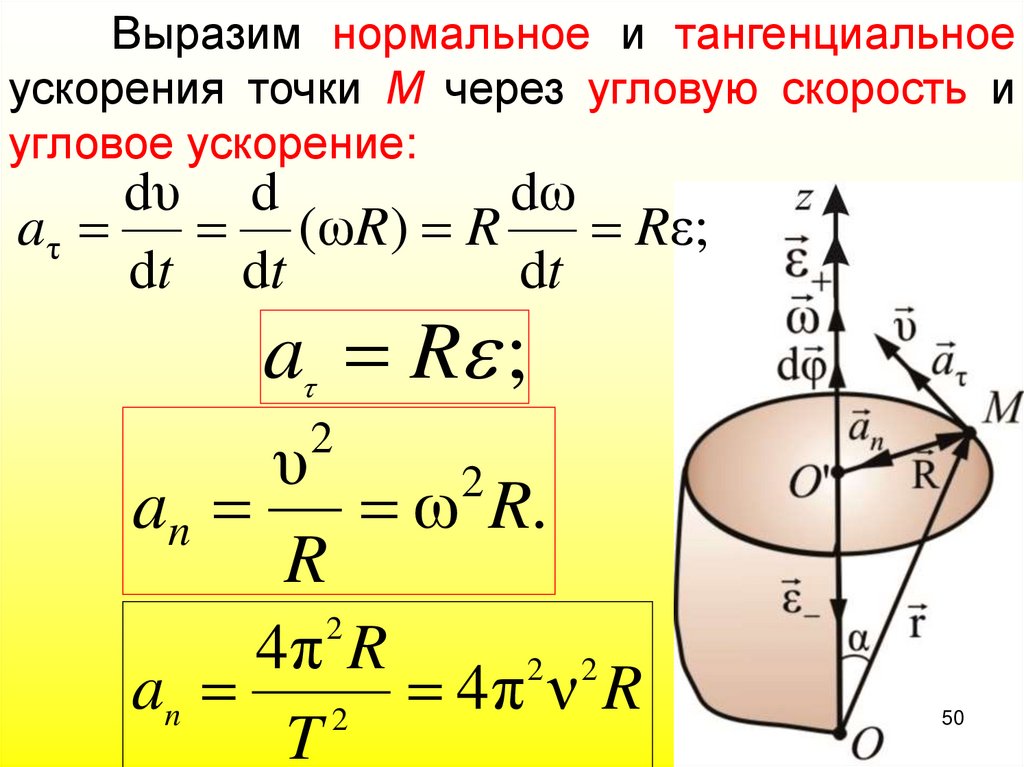

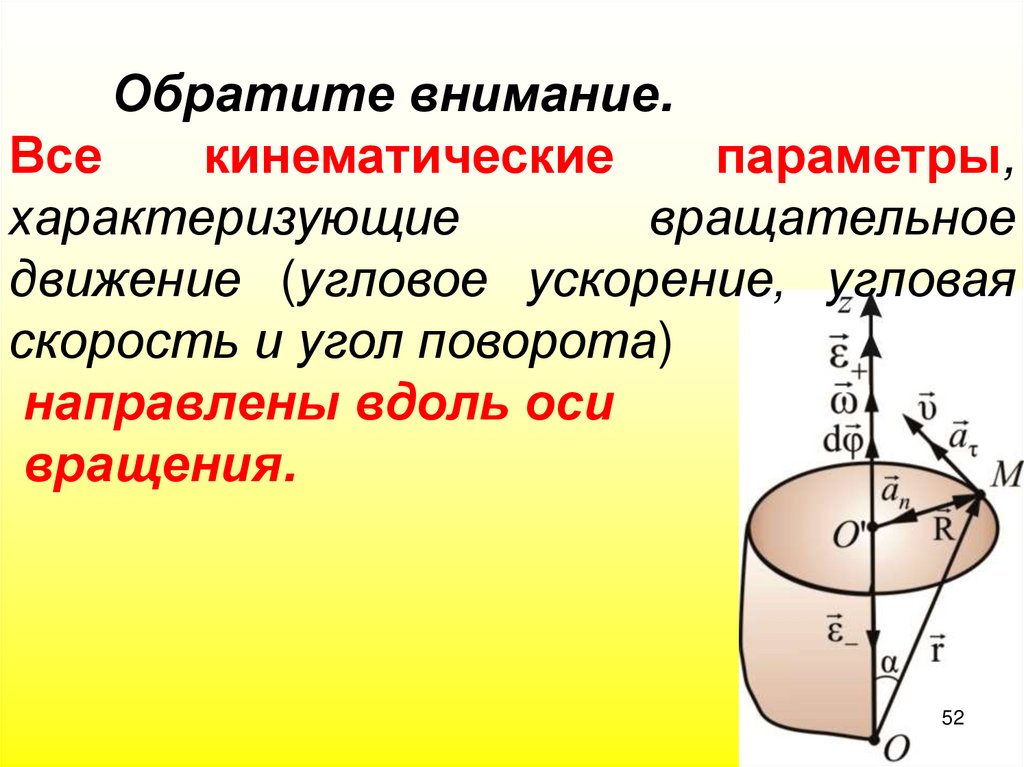










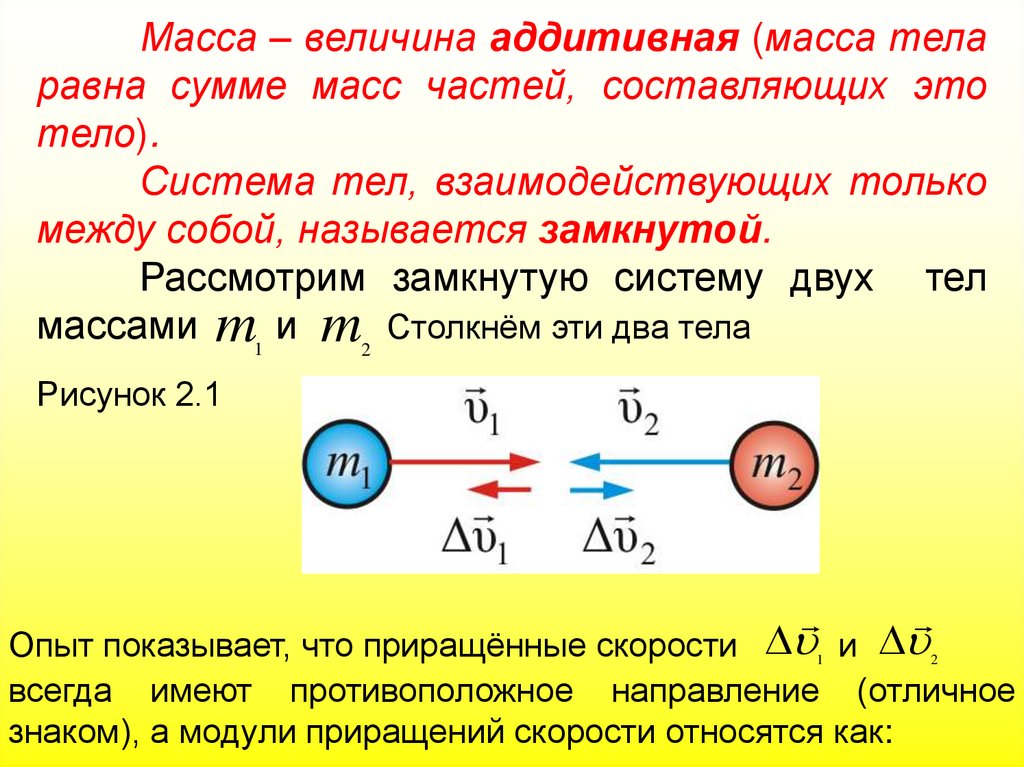
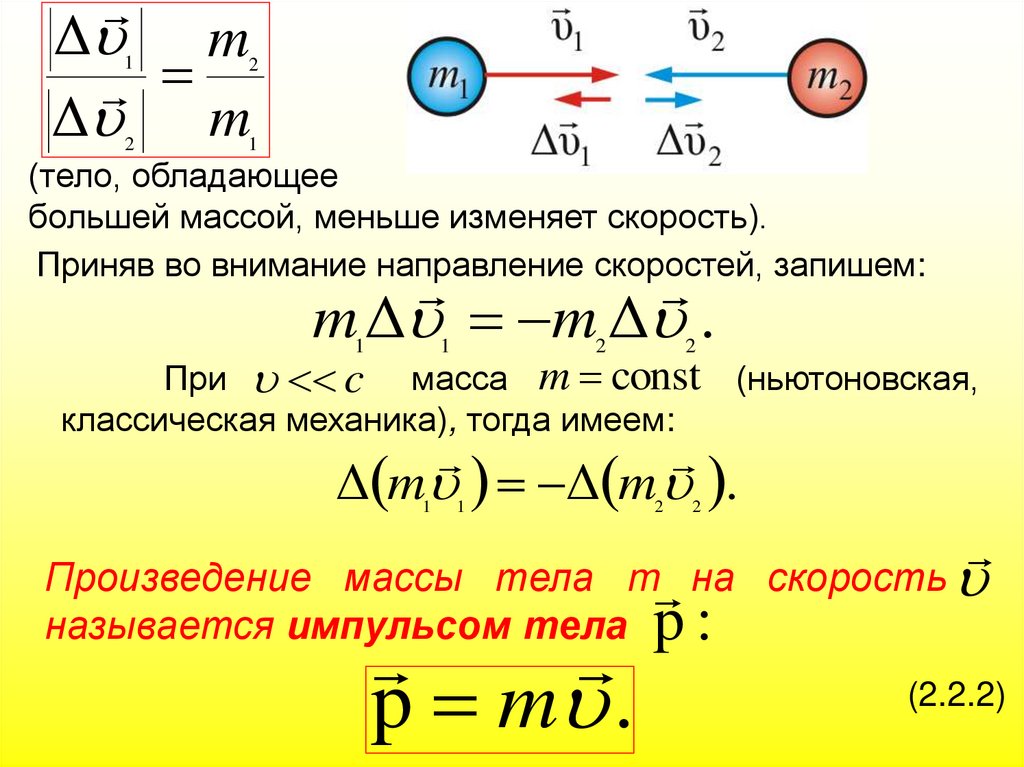





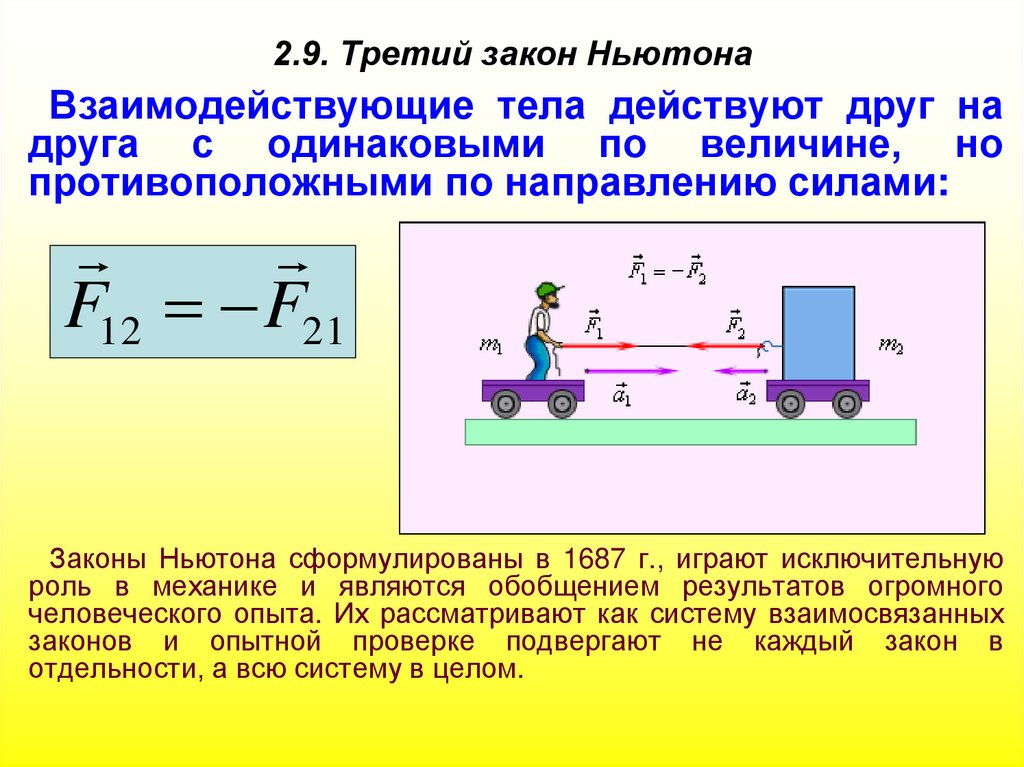
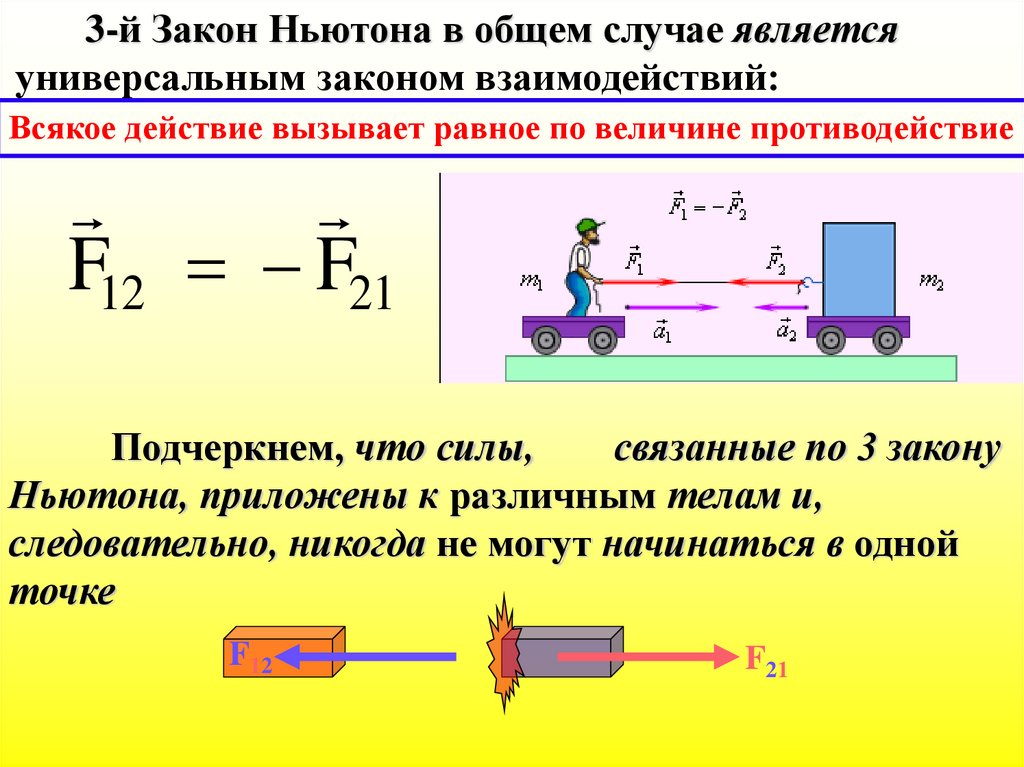

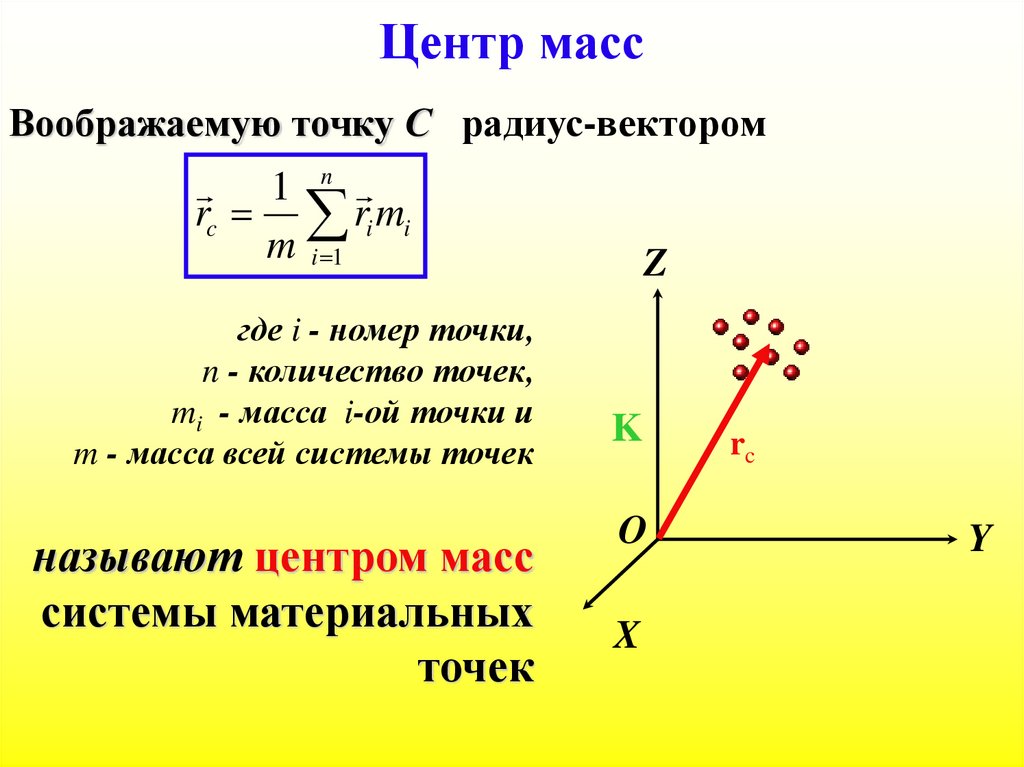
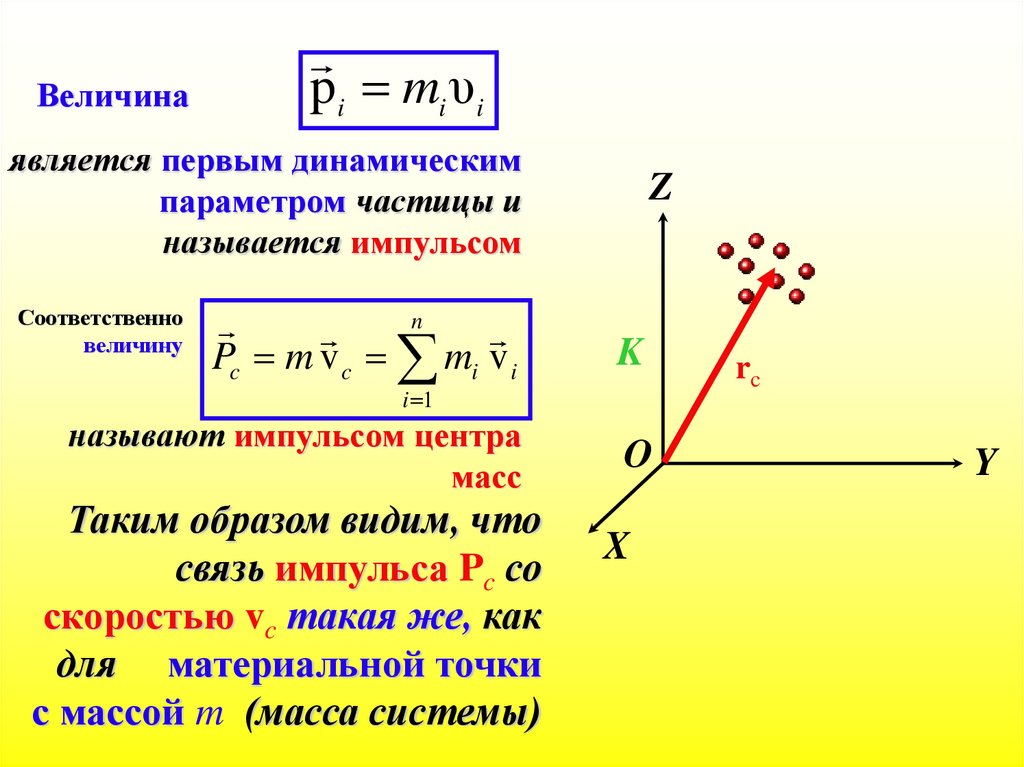





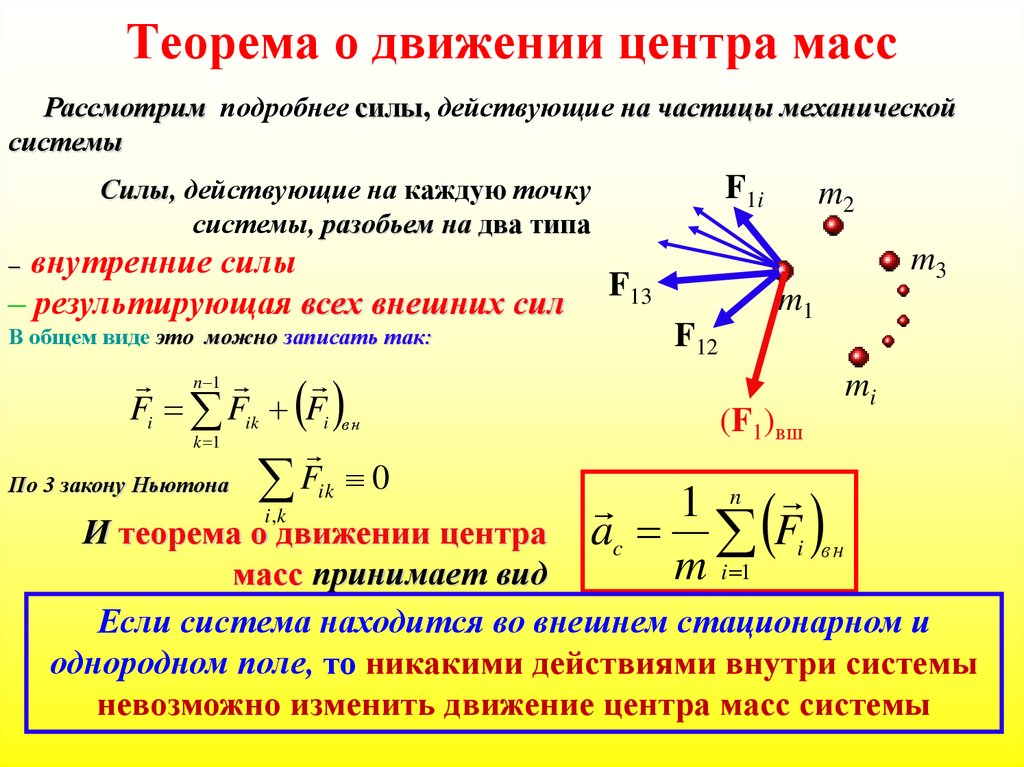




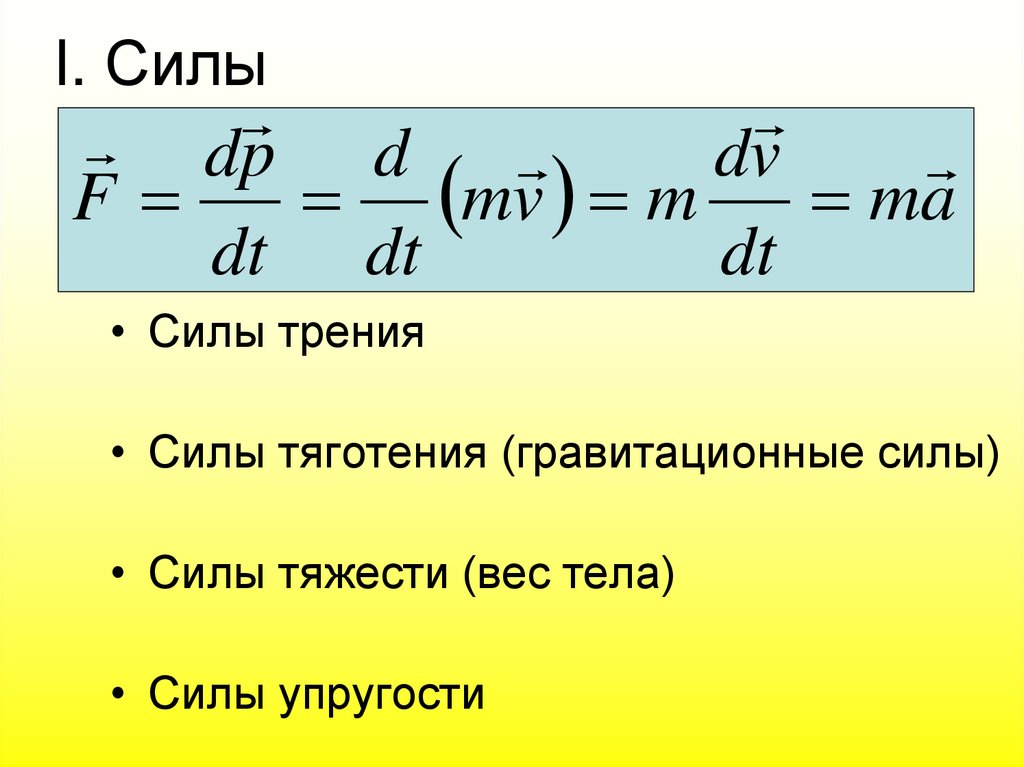




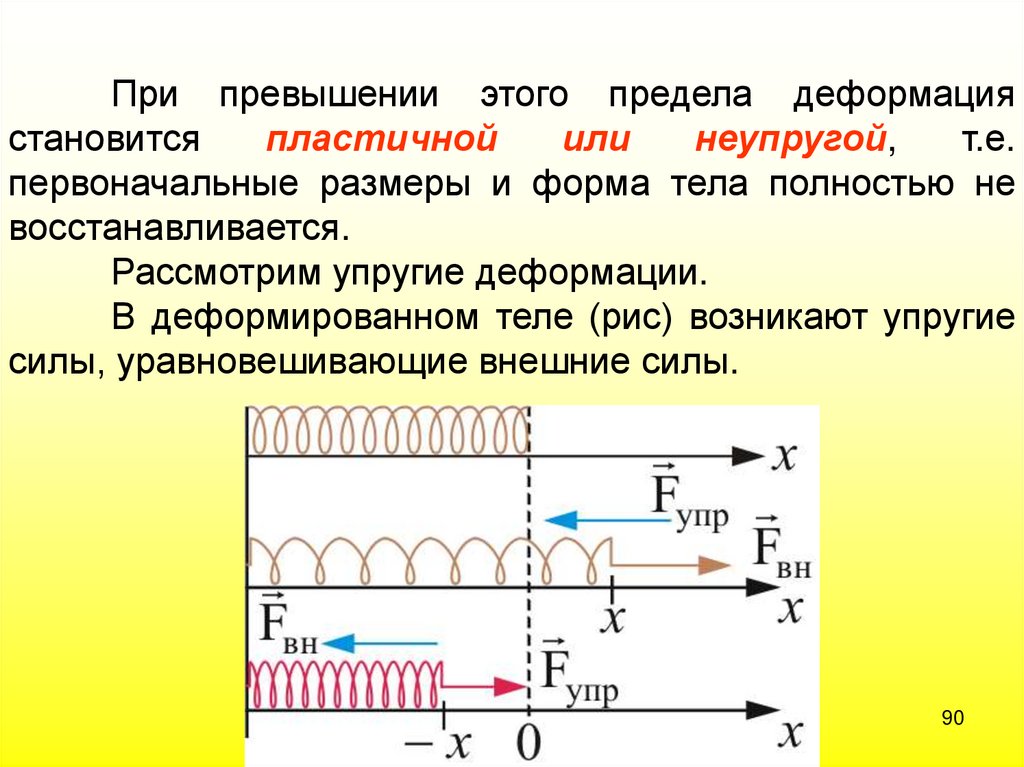
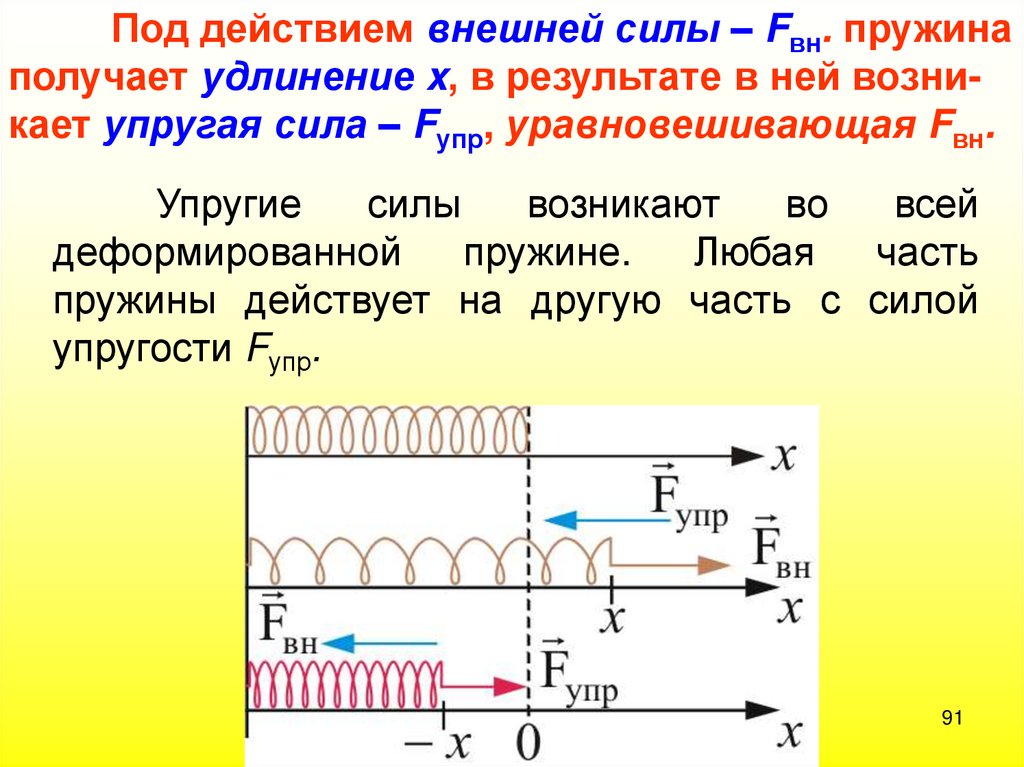



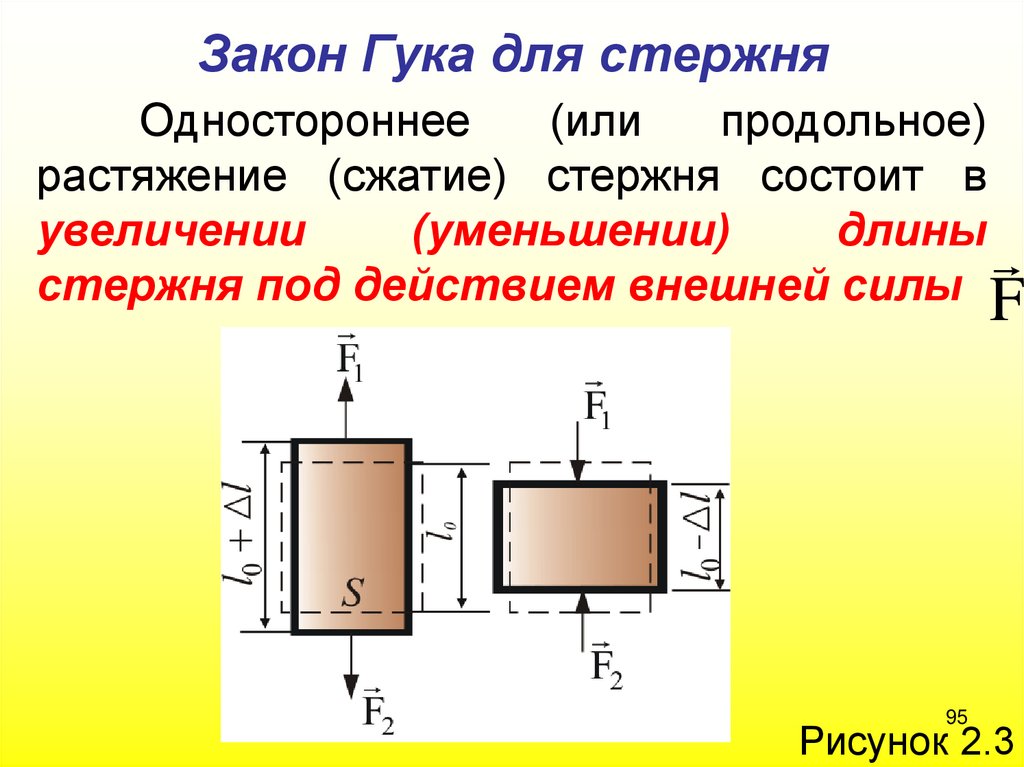

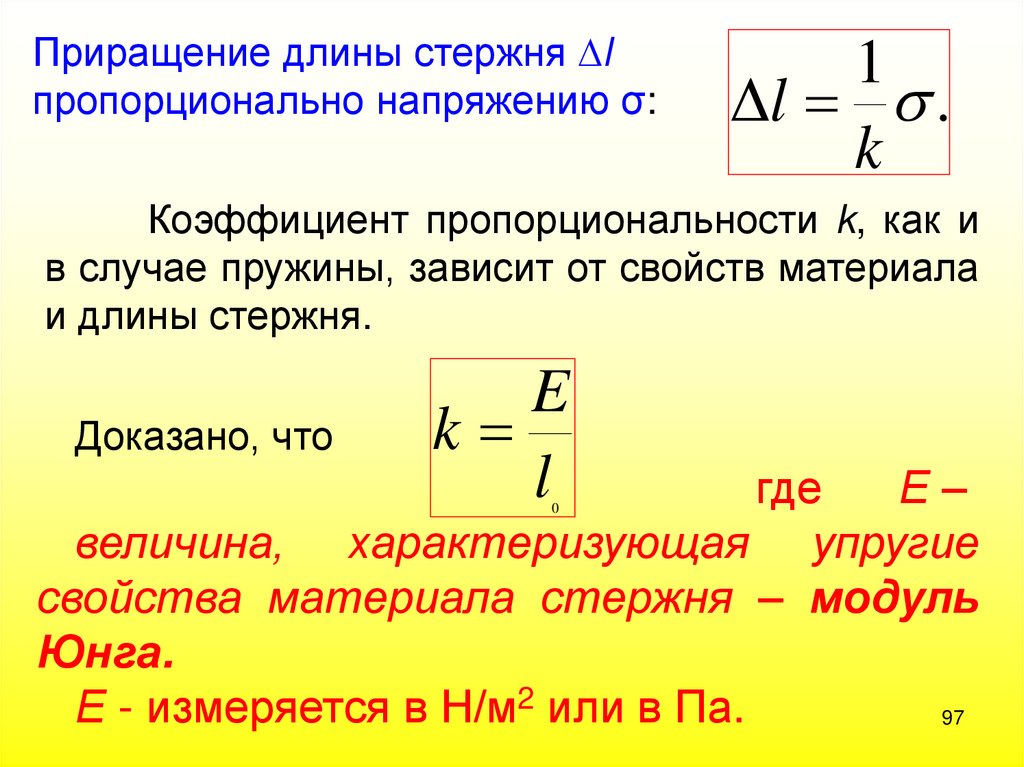
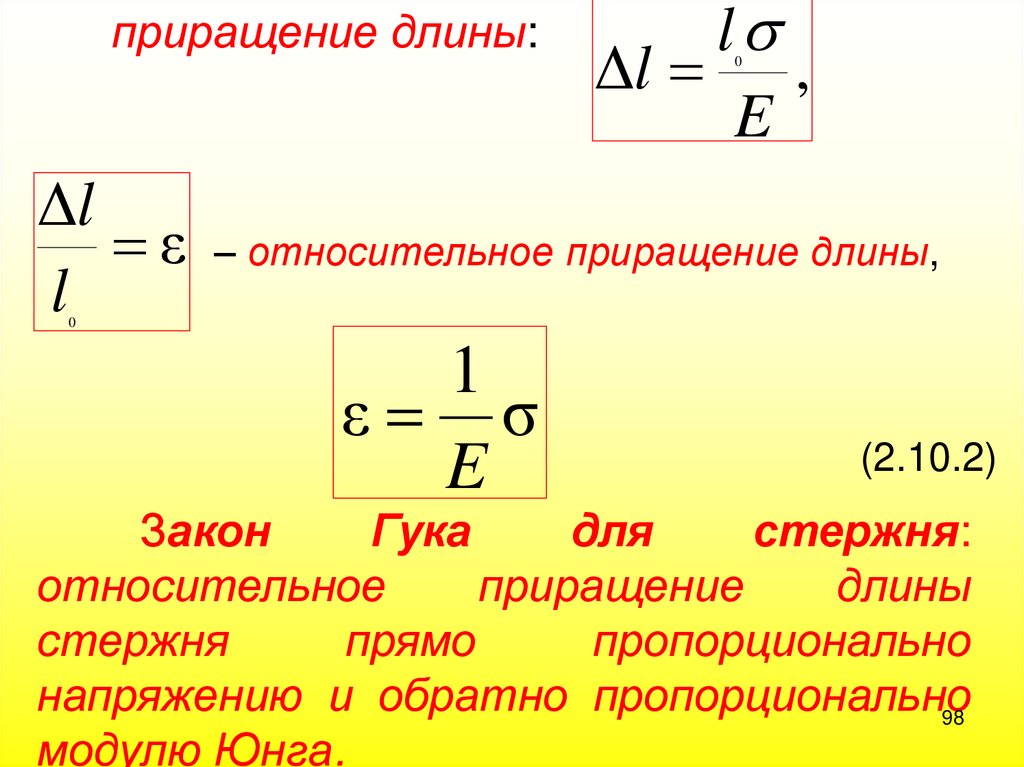
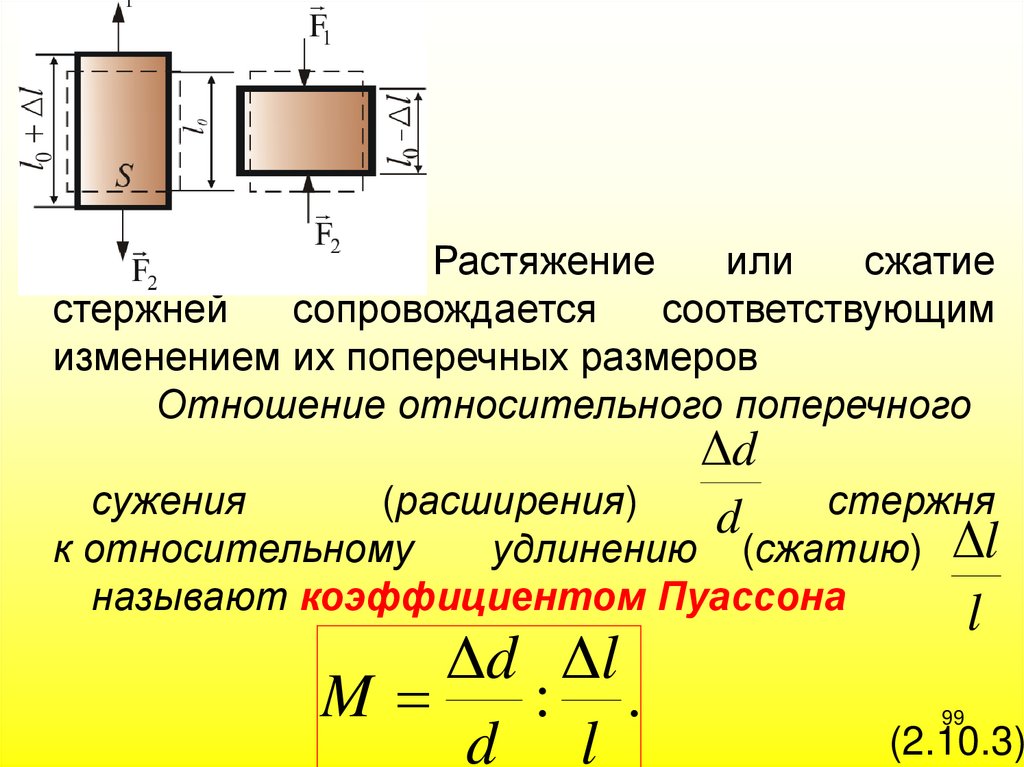

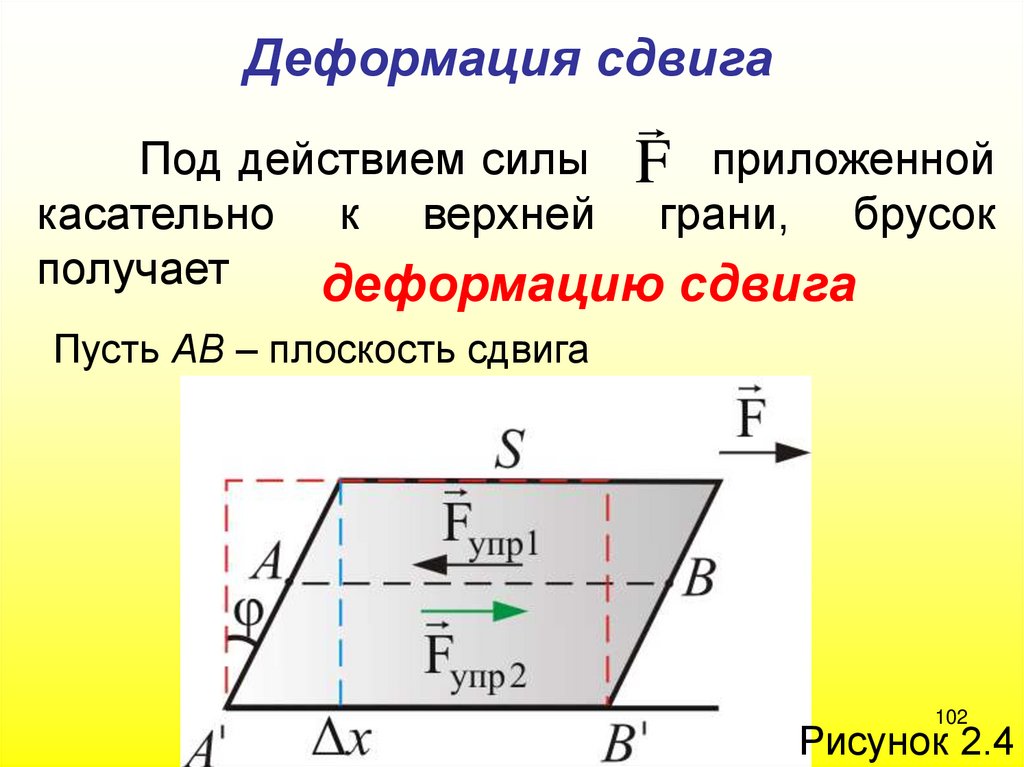



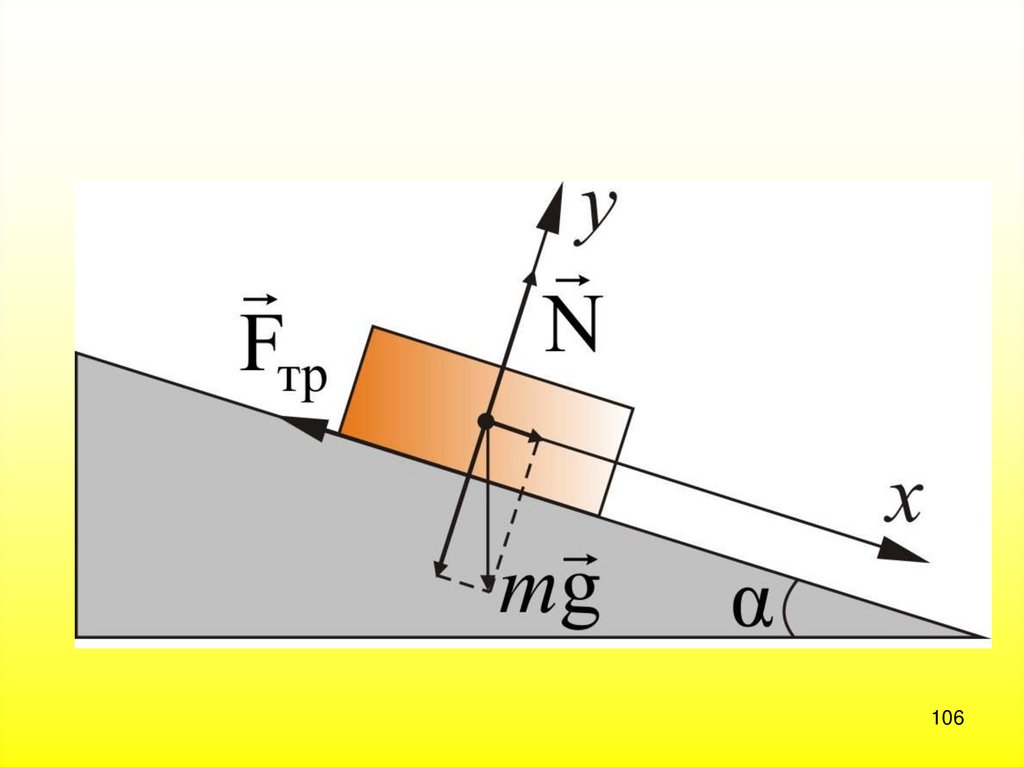
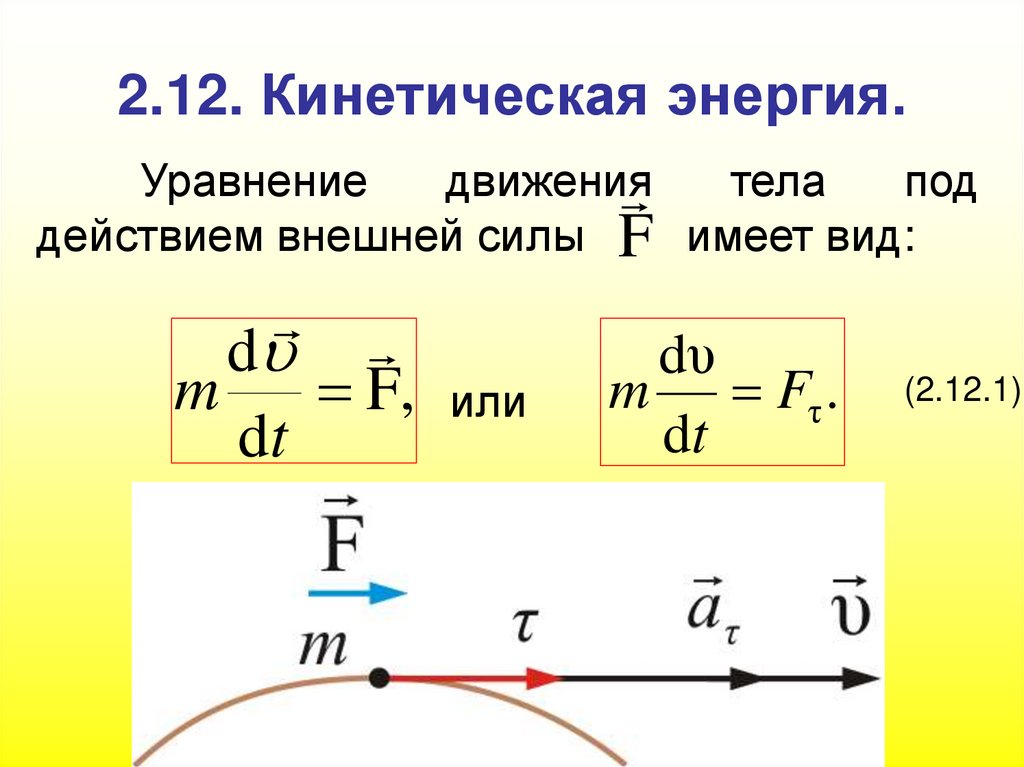


















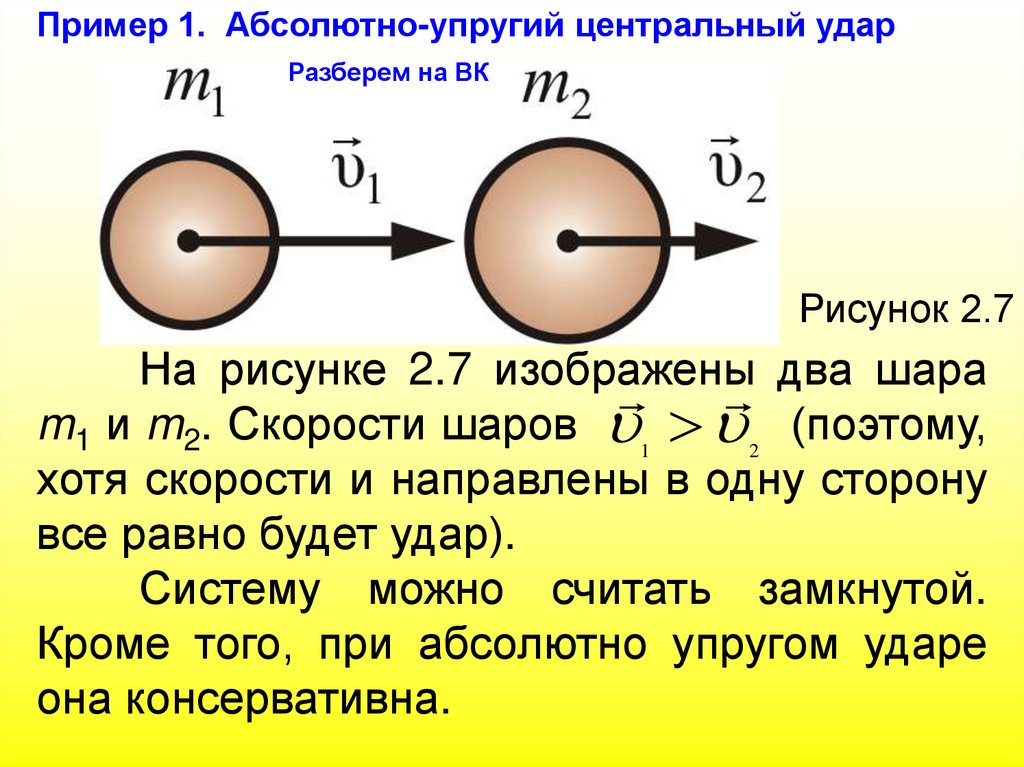


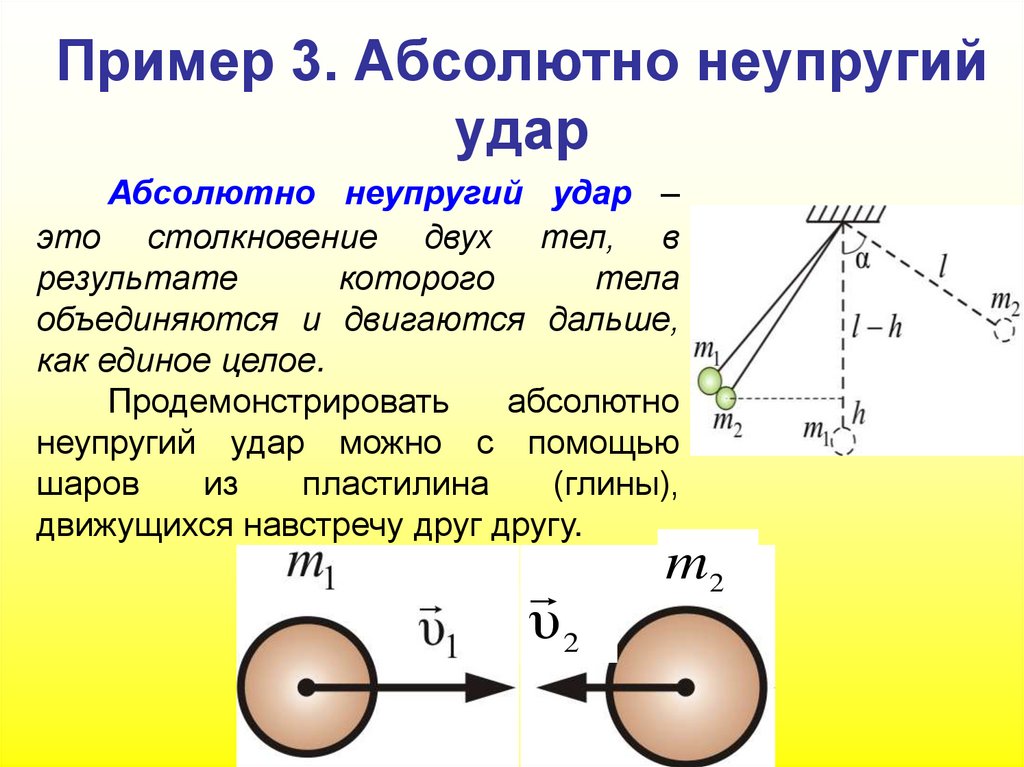




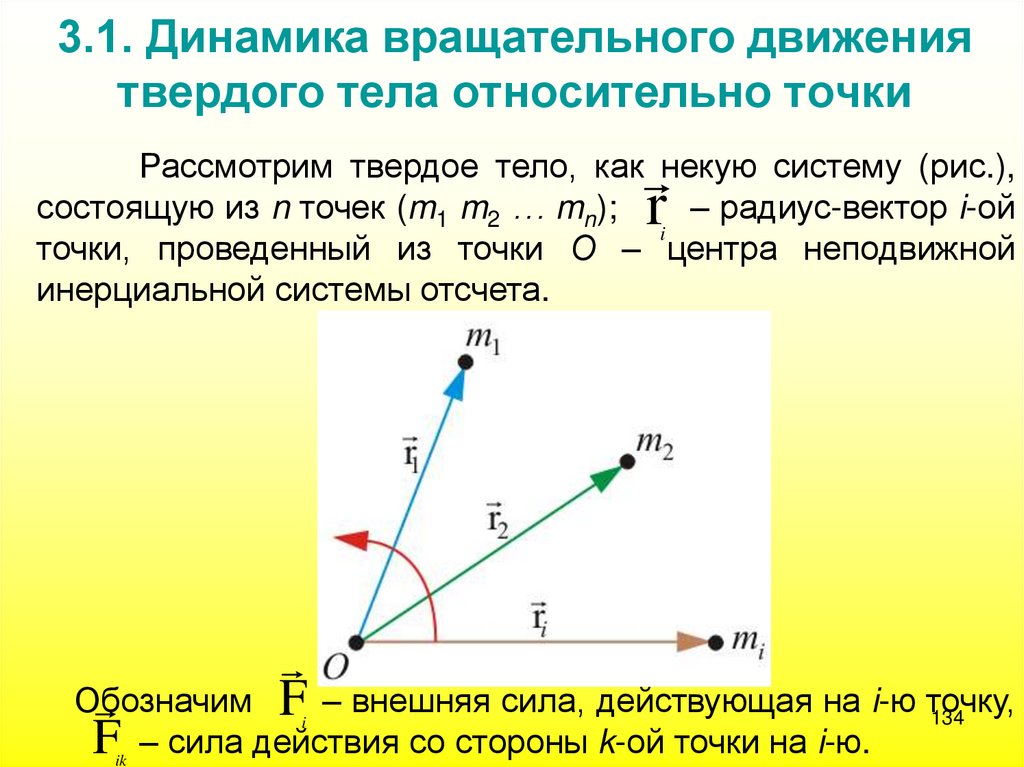
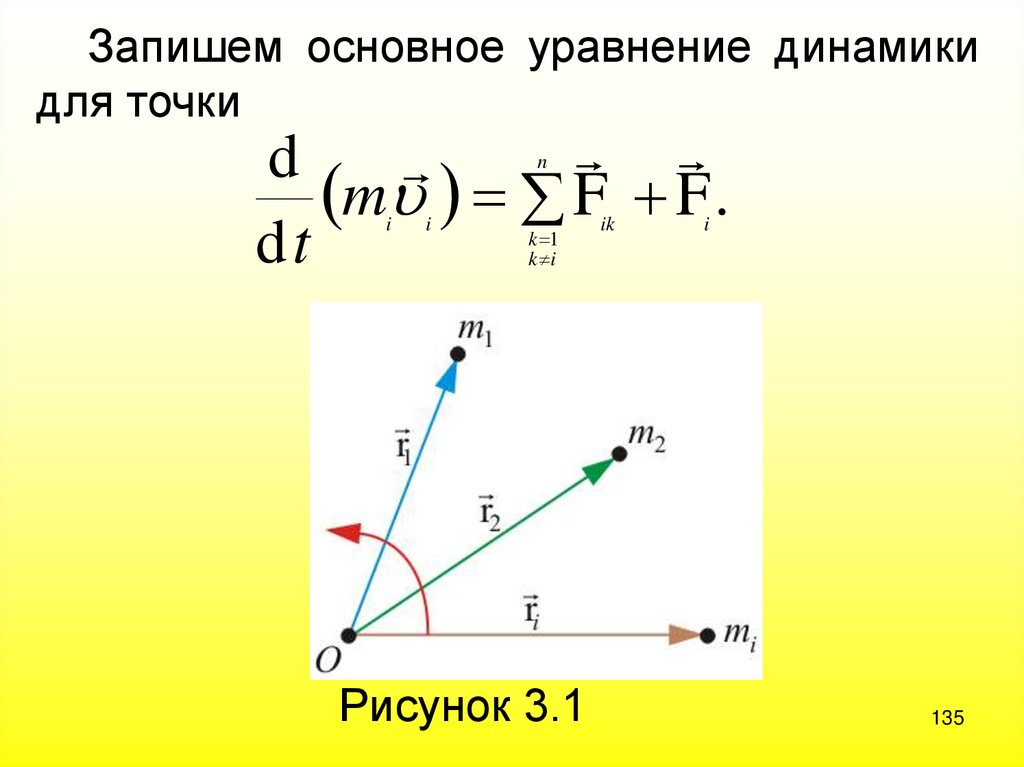
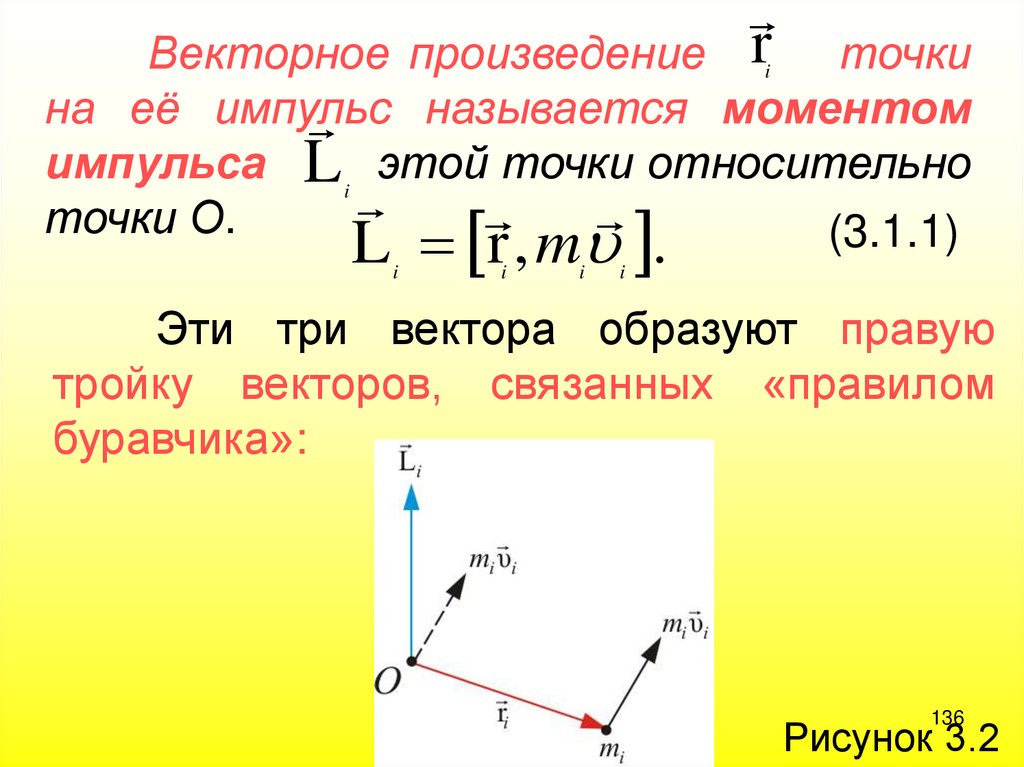
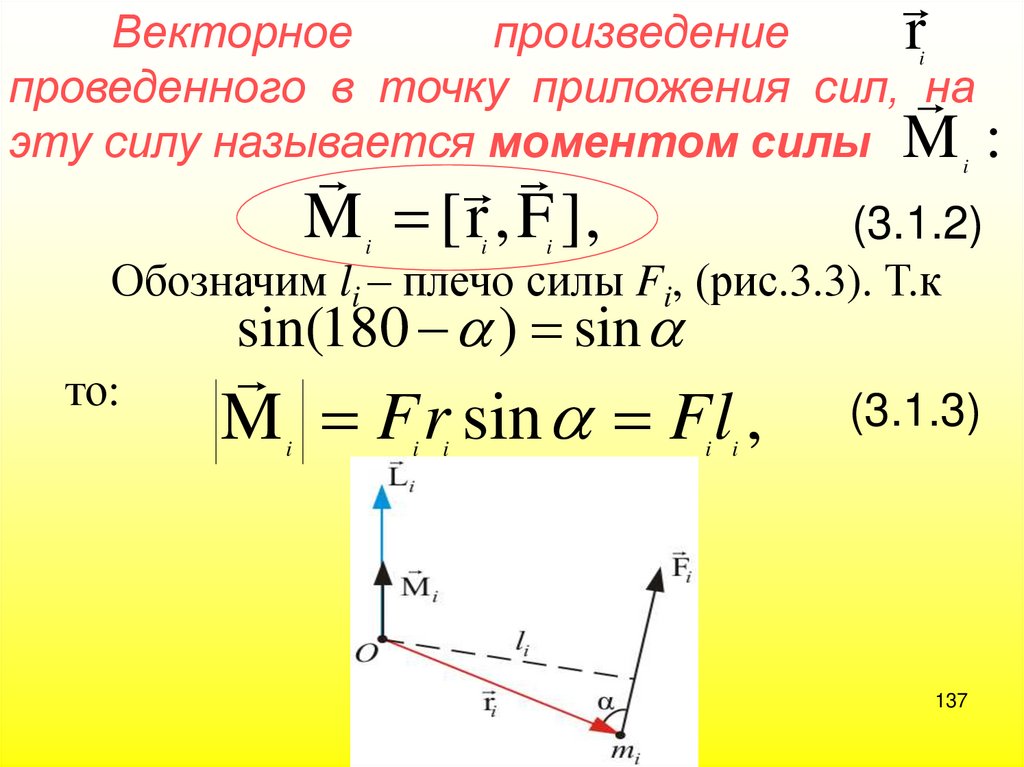




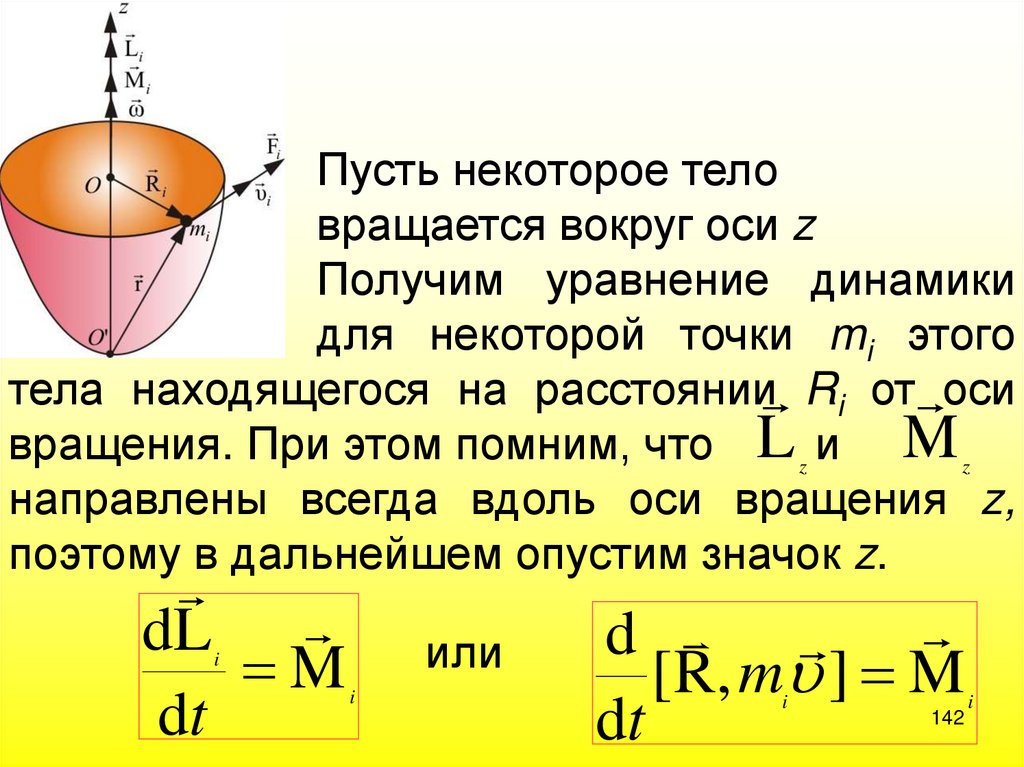
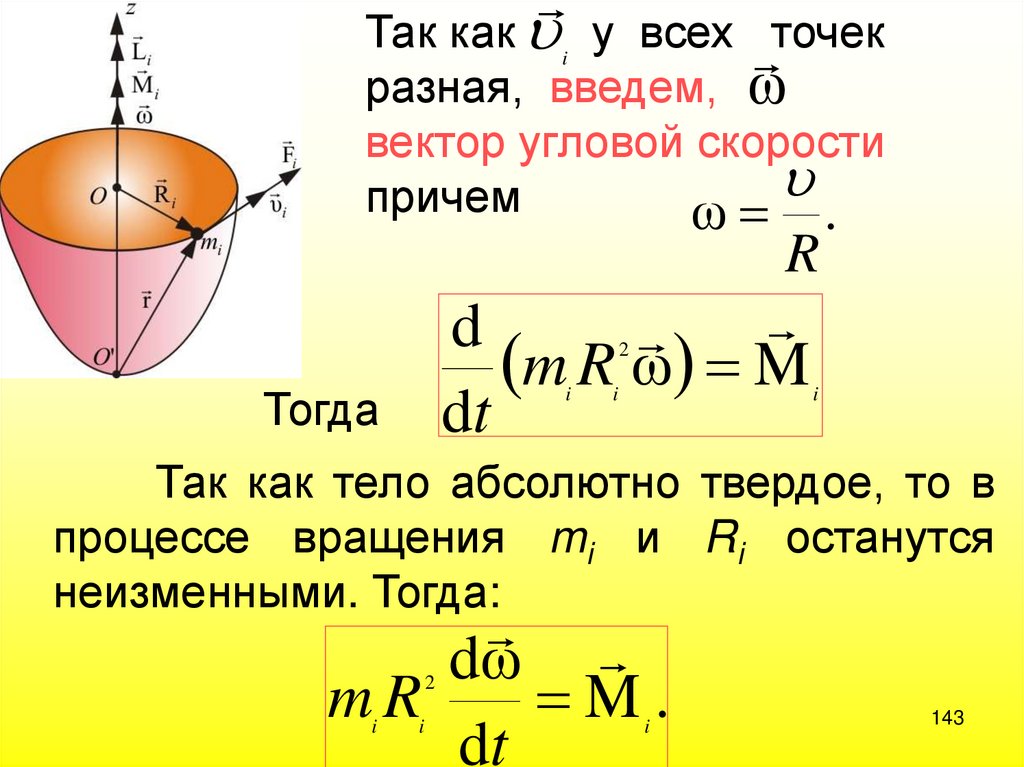
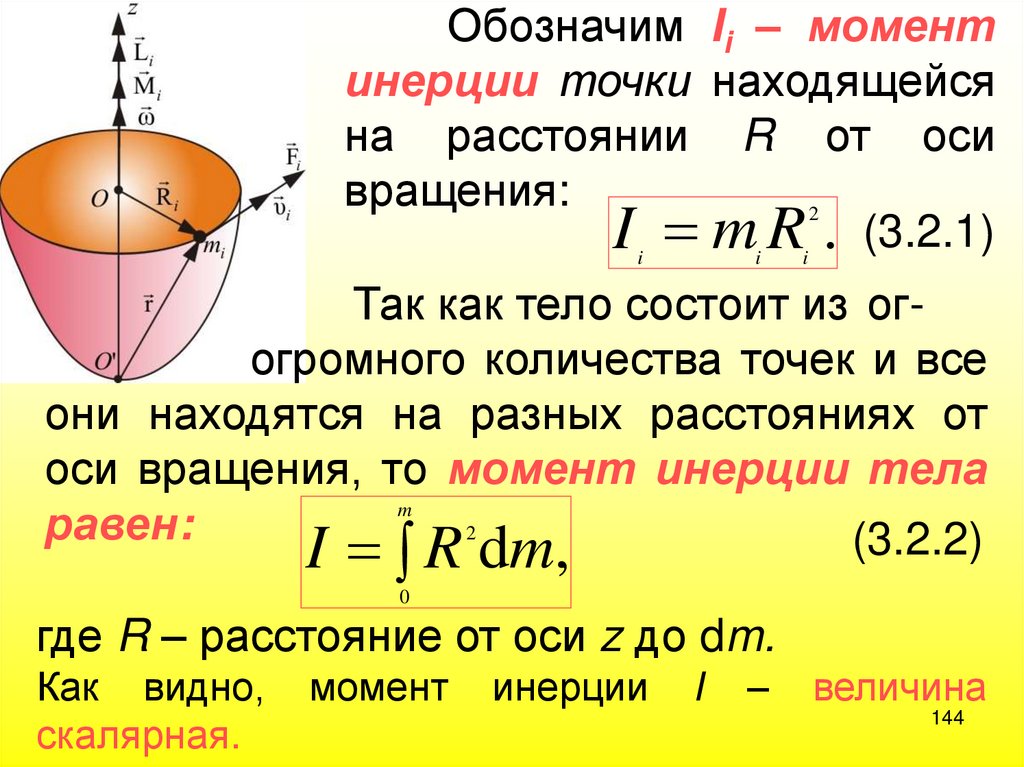
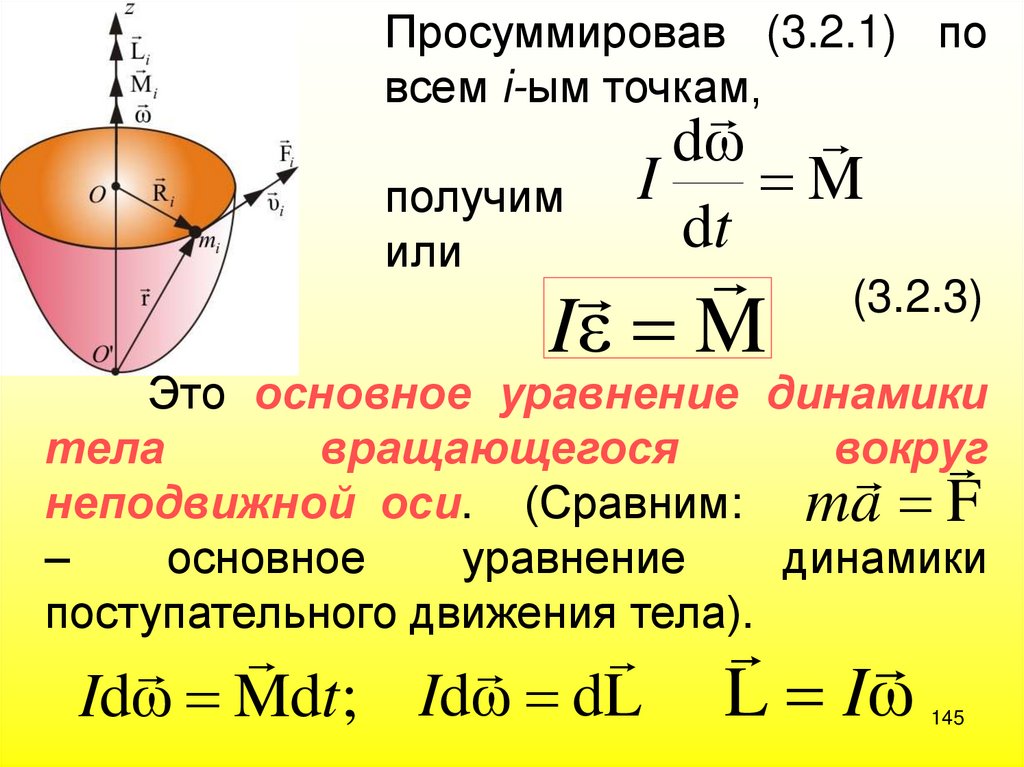
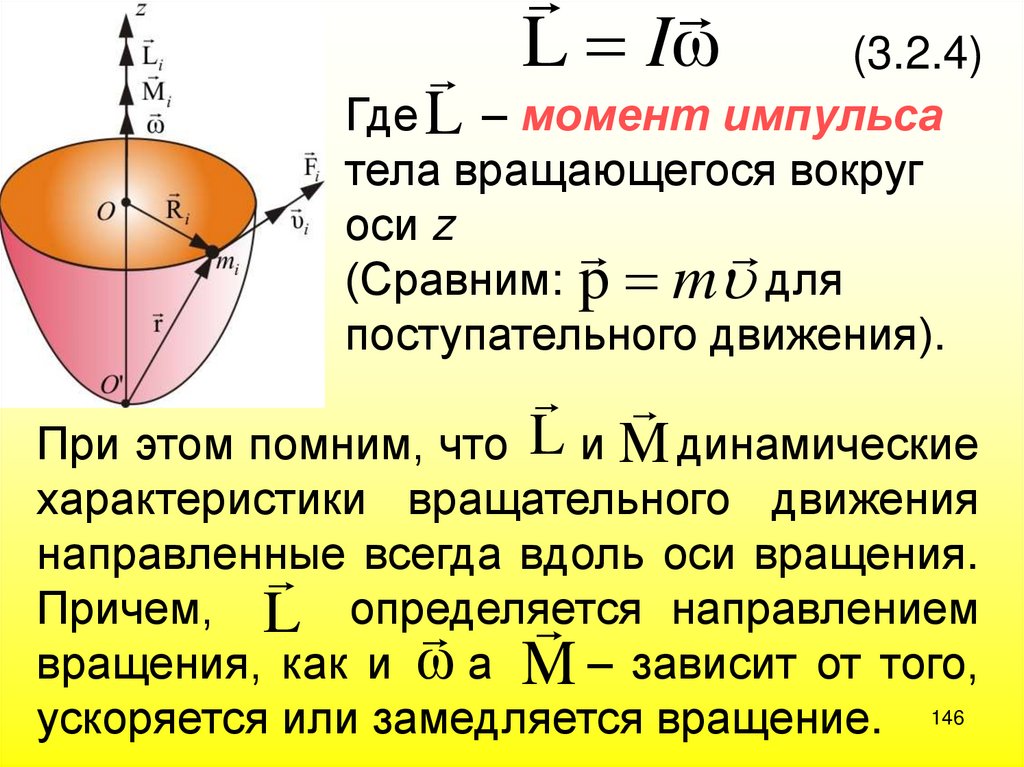

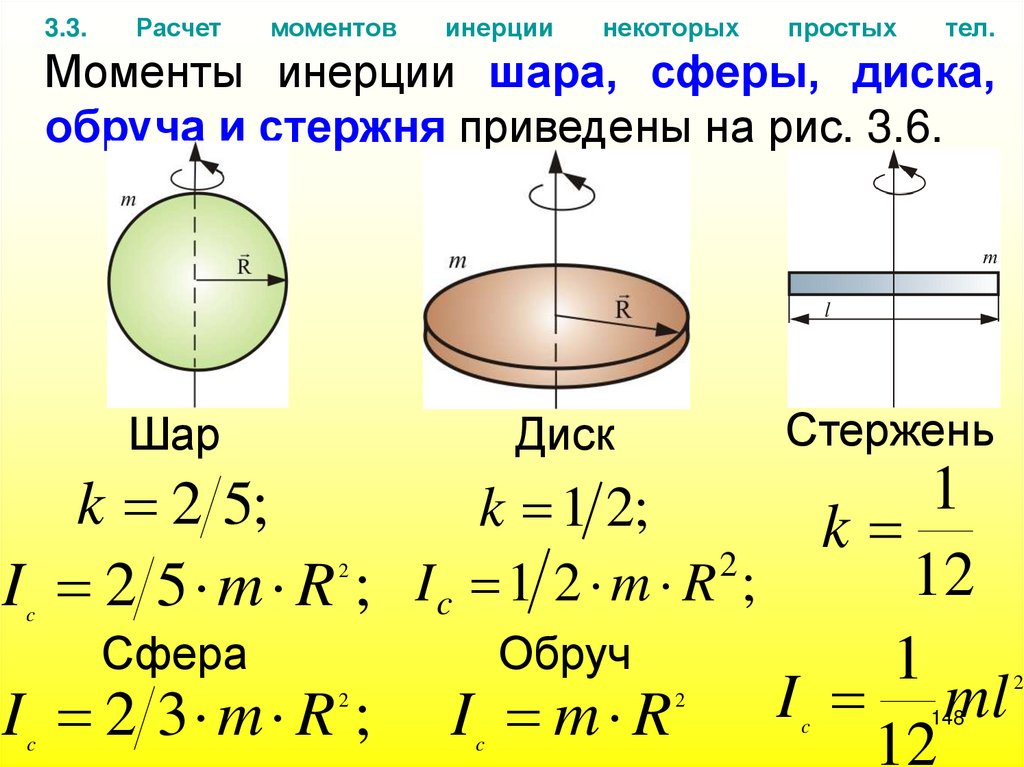






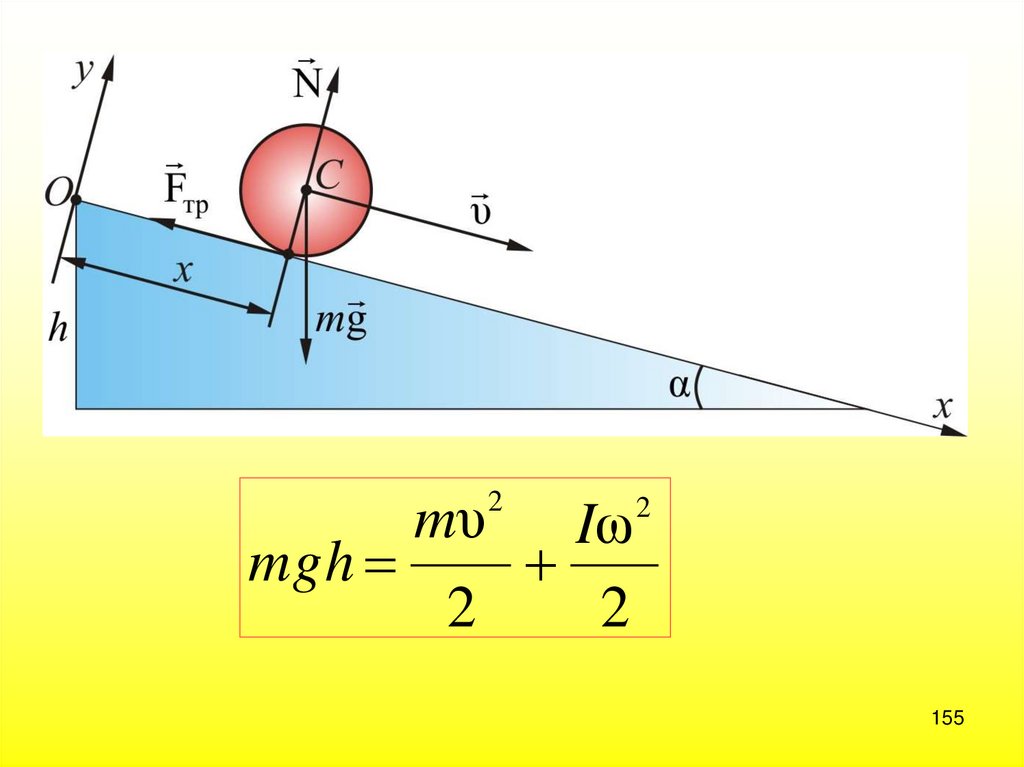



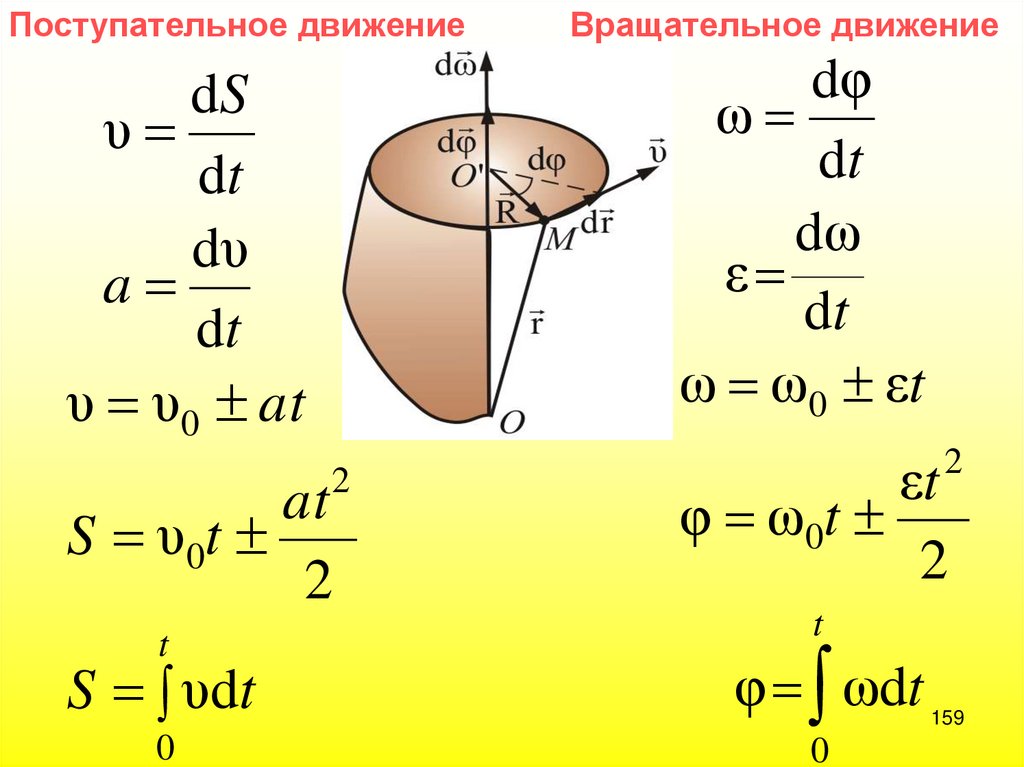
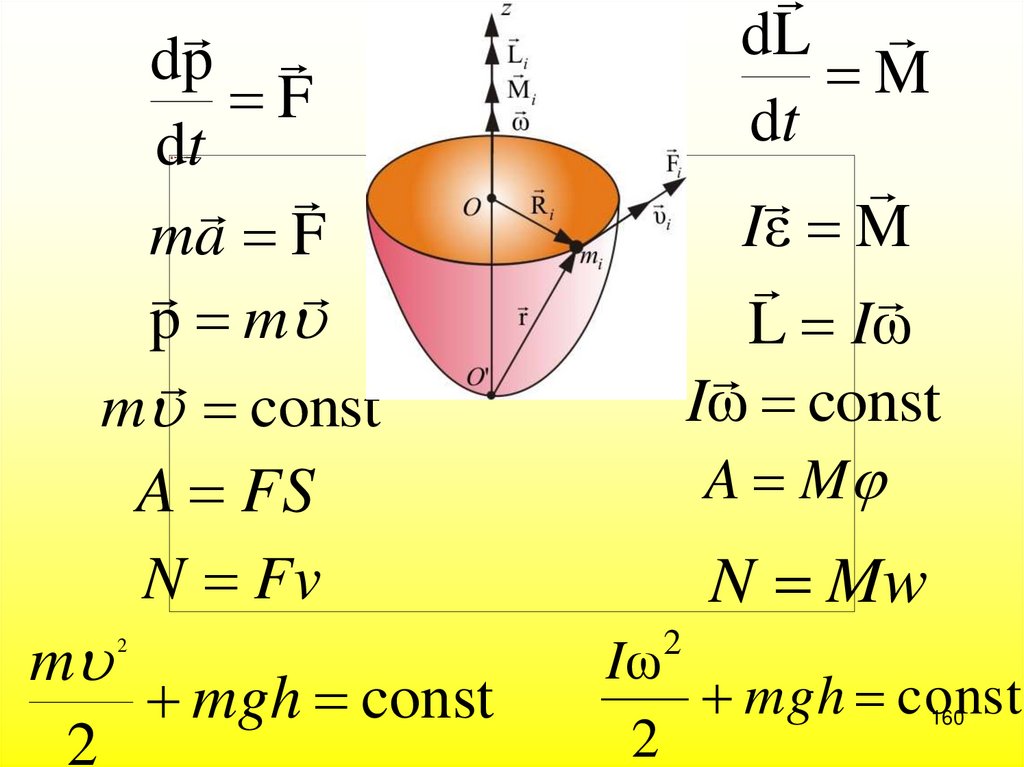









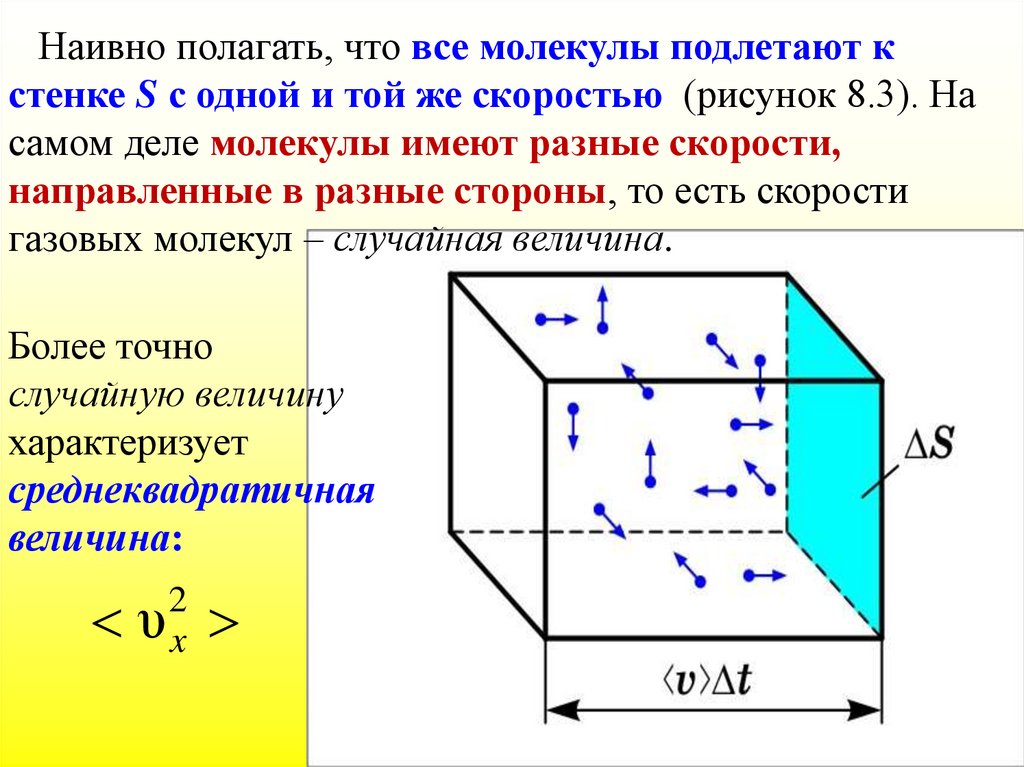








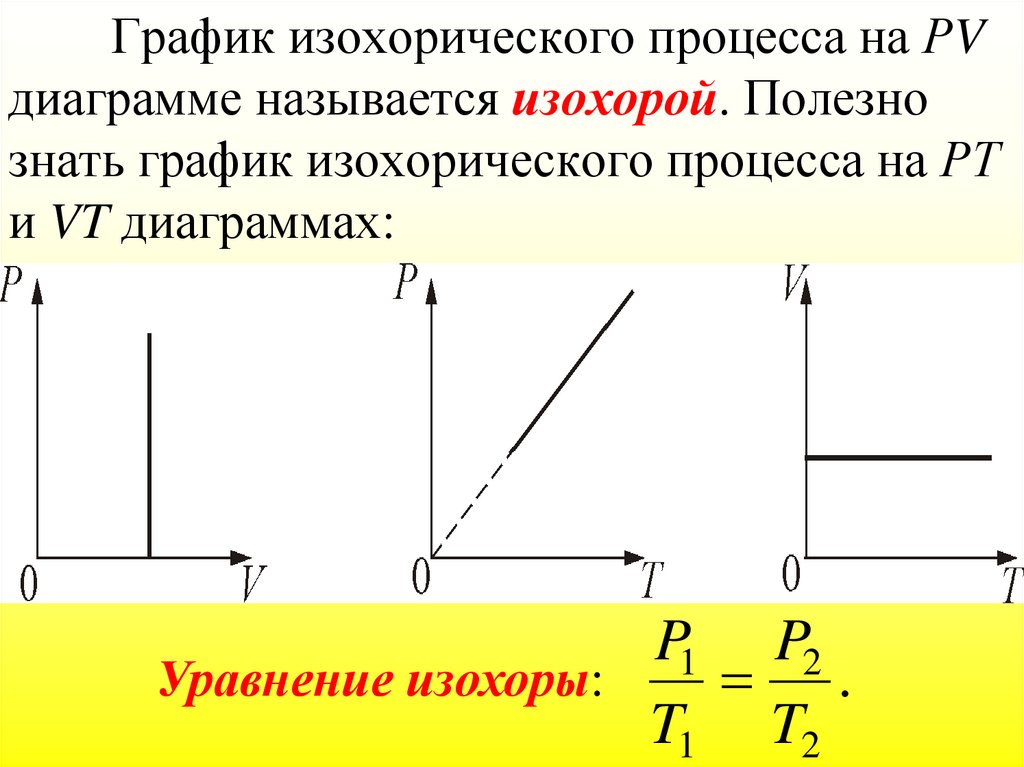



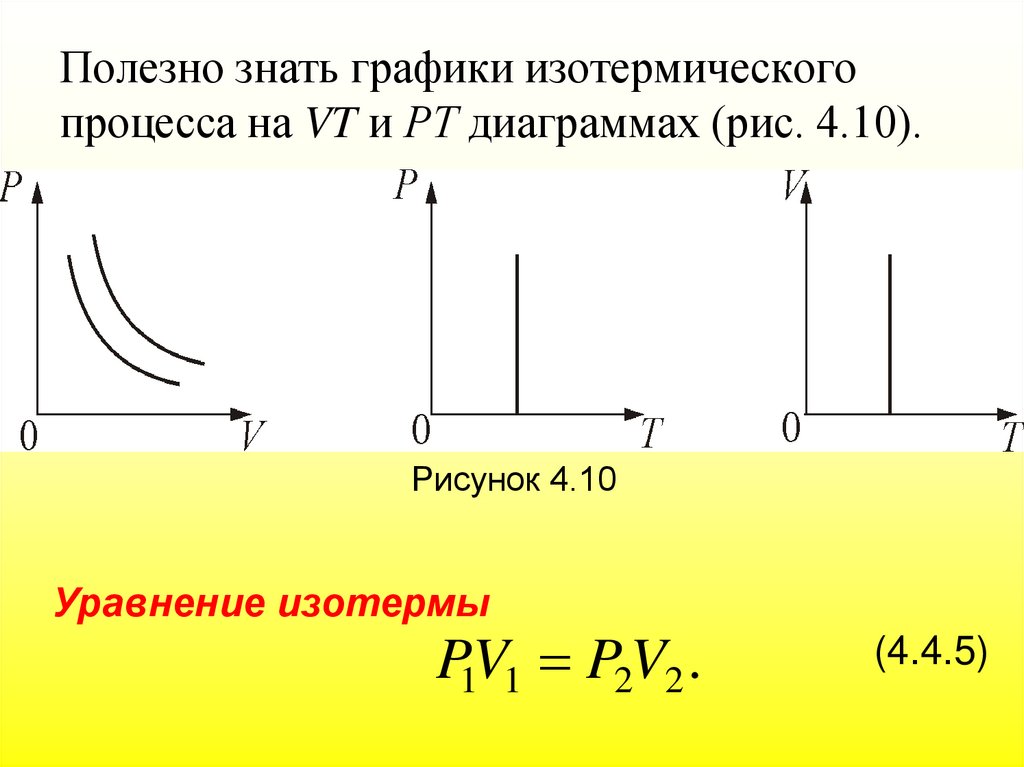
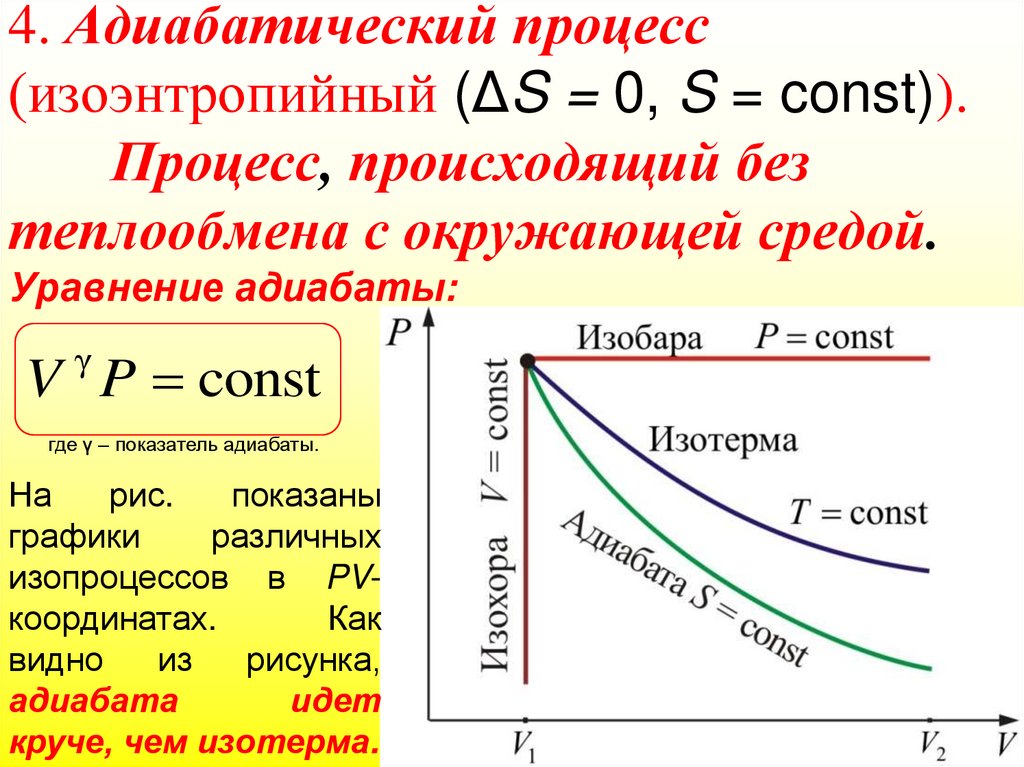




















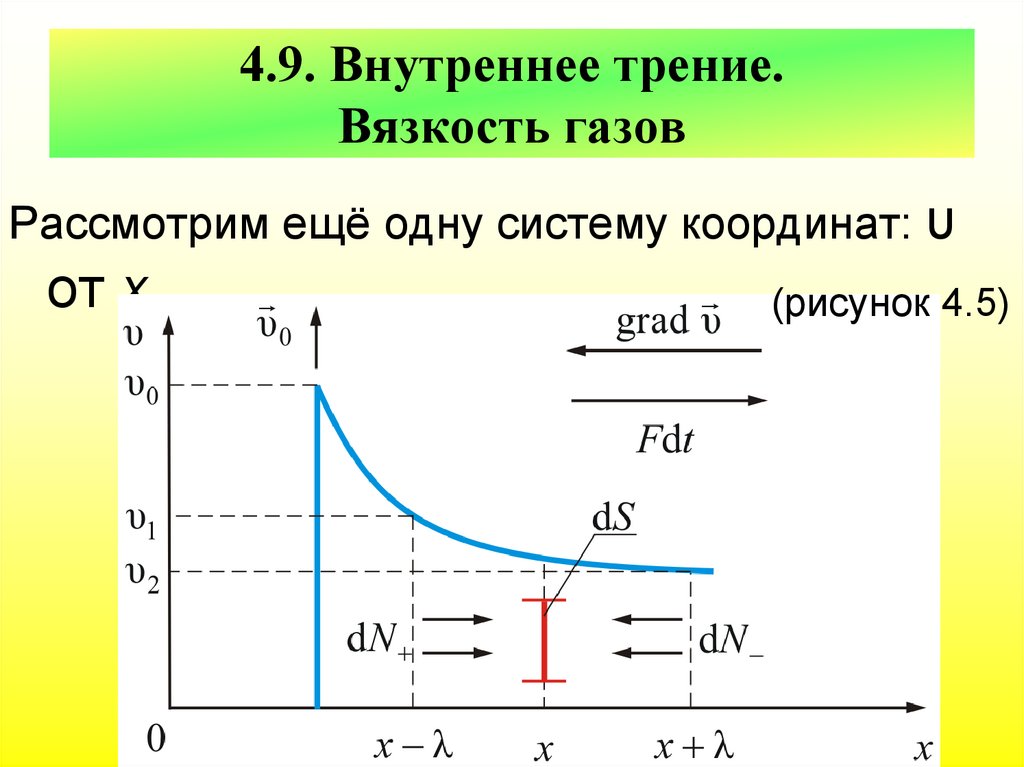











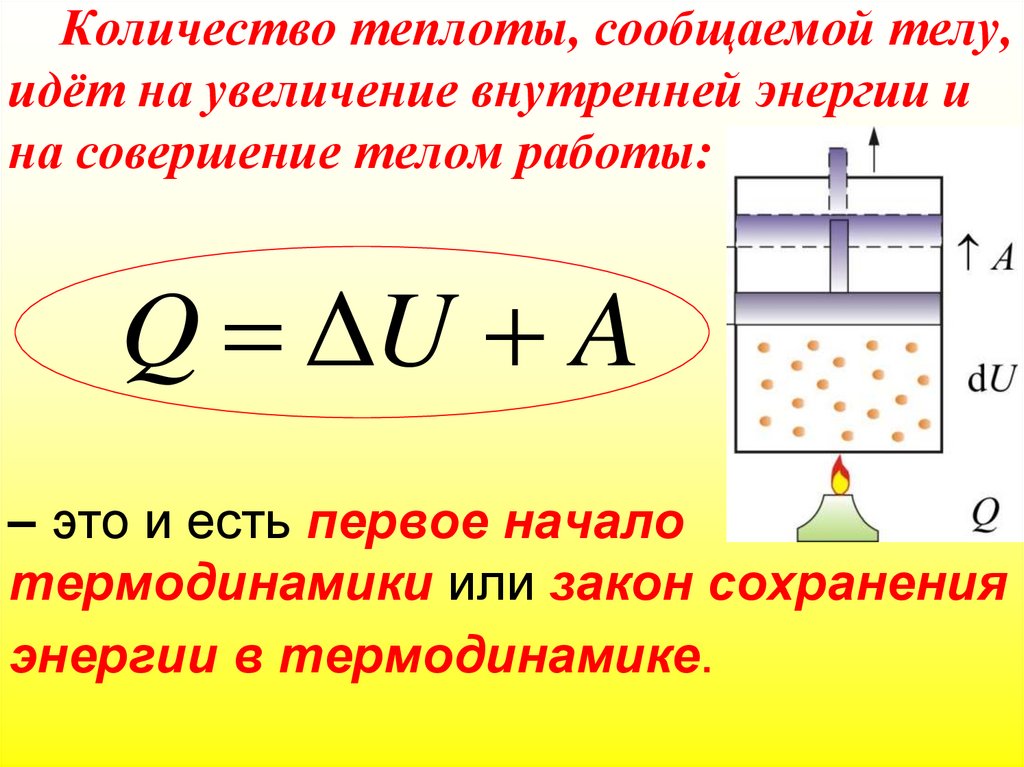


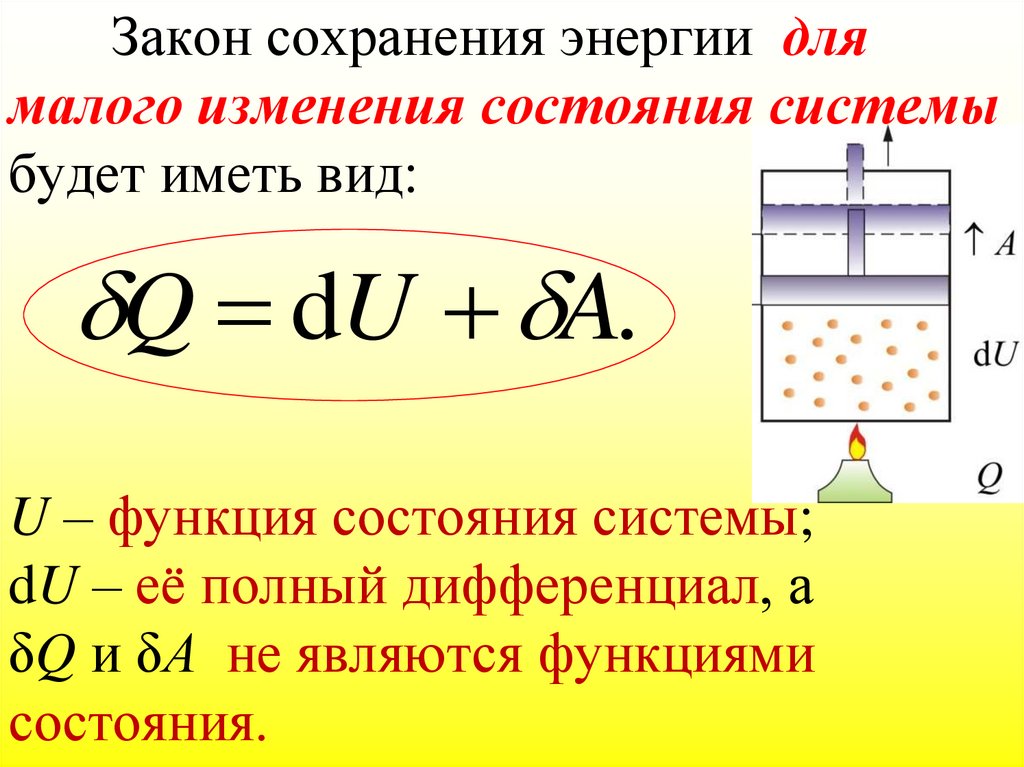

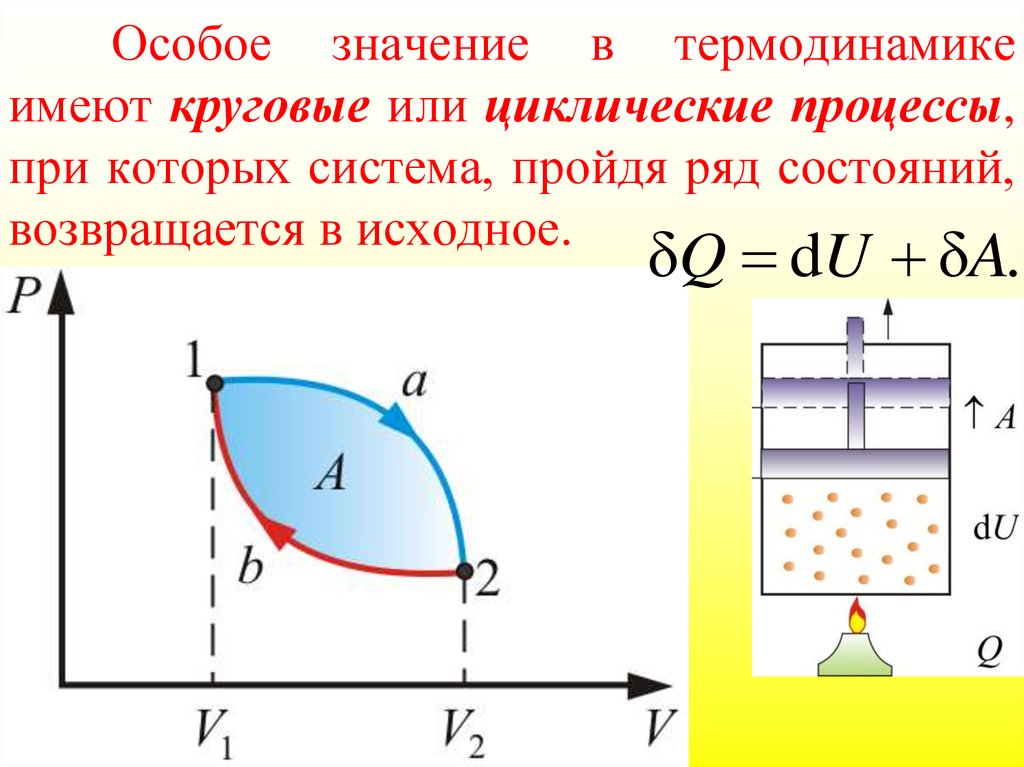


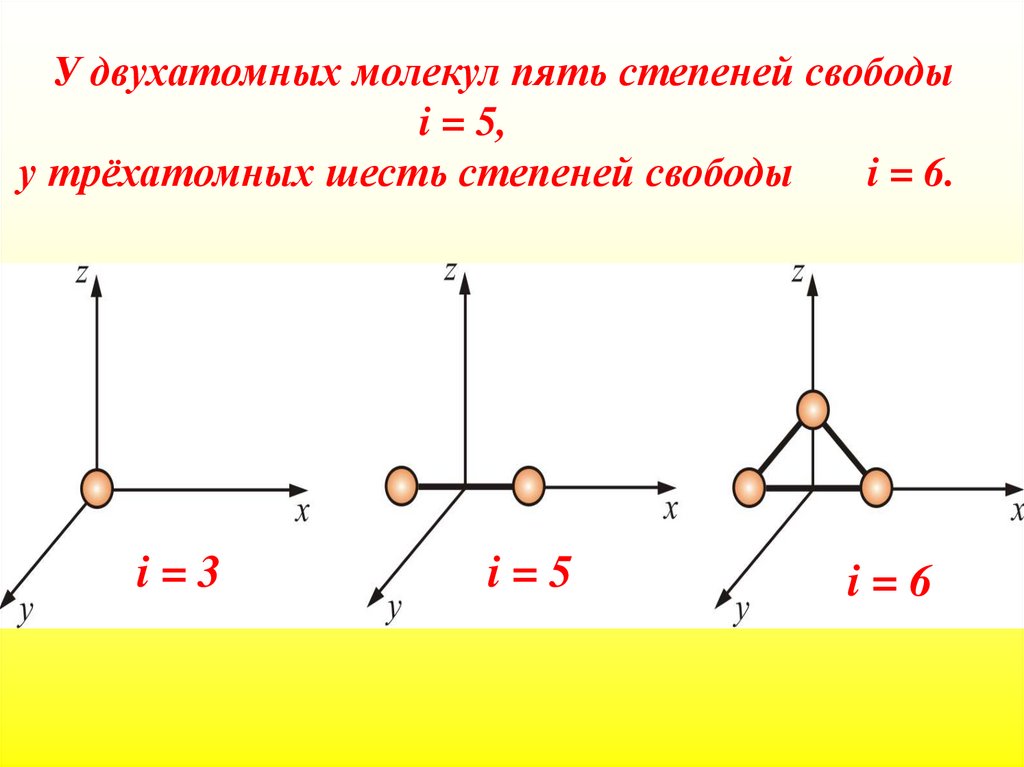







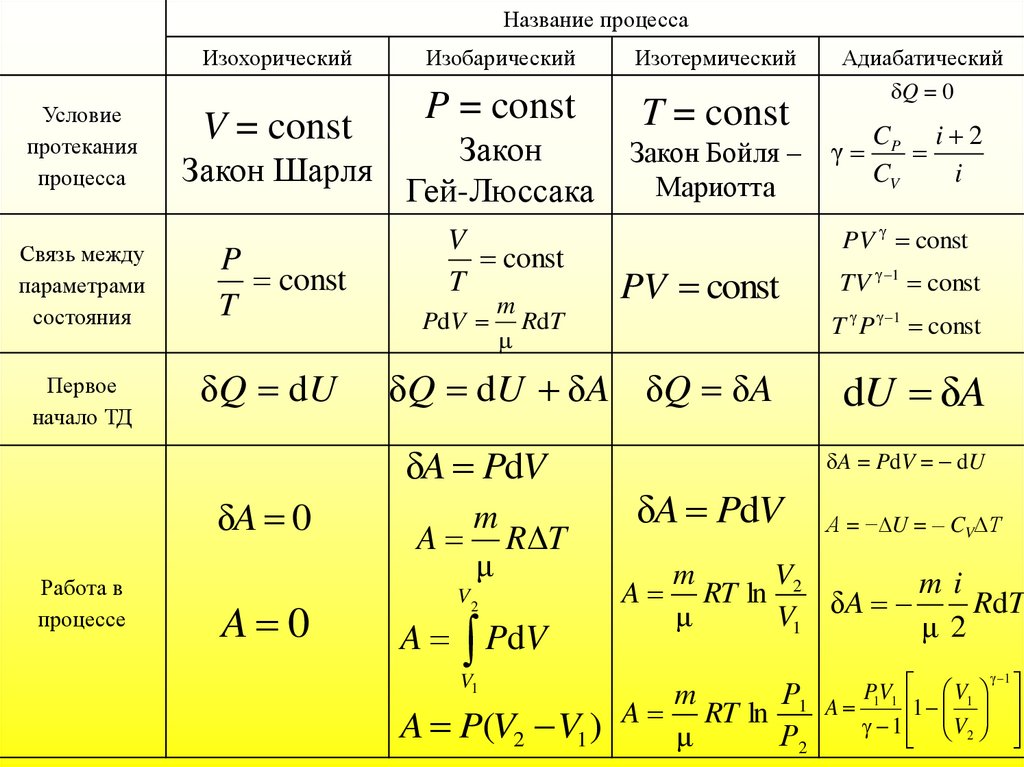

 physics
physics








