Геометрия Лобачевского

1. Геометрия Лобачевского

Для студентов 2 курса
математического факультета
(сост. доц. М.С. Ананьева)

2. 7. Треугольники

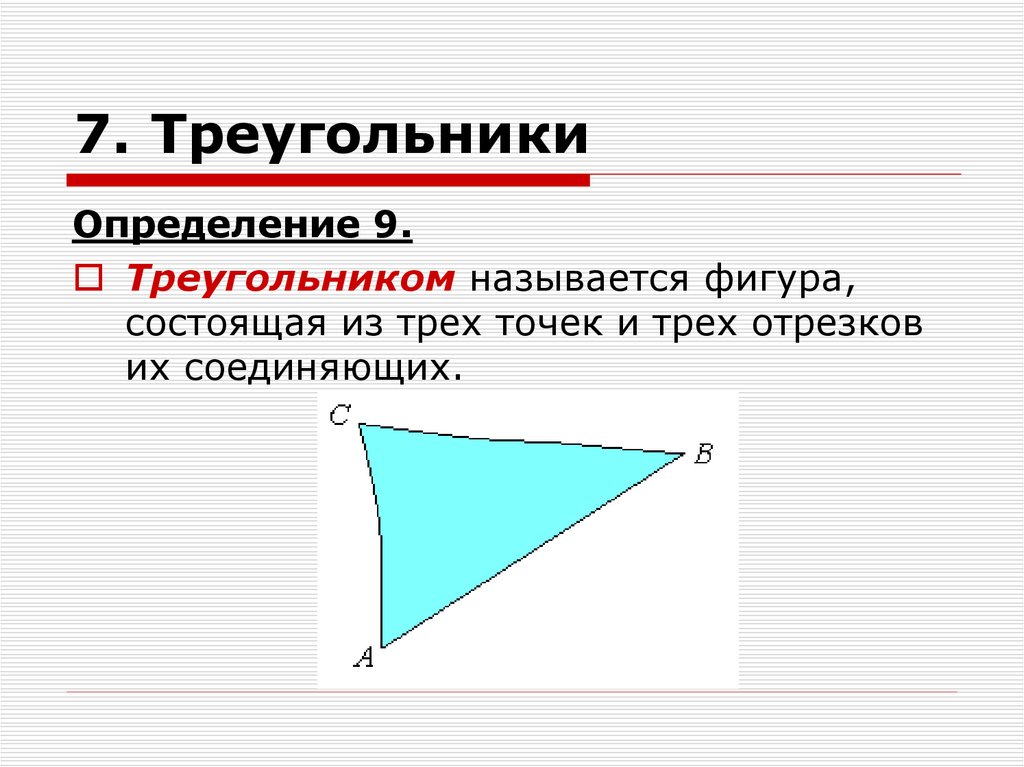
Определение 9.
Треугольником называется фигура,
состоящая из трех точек и трех отрезков
их соединяющих.

3. 7. Треугольники

Теорема 3. Саккери–Лежандра
(Эквивалент V постулата)
Если в одном треугольнике
сумма углов равна 2d, то сумма
углов любого треугольника
равна 2d.
(без доказательства, Ат-Ч.2, С.250)

4. 7. Треугольники

Определение 10.
Дефектом треугольника АВС называется
число
АВС 2d ABC
где
( ABC ) А В С
сумма мер углов АВС.
(7.1)

5. 7. Треугольники. Свойства дефекта треугольника

1. В евклидовой геометрии дефект любого
треугольника равен 0.
Доказательство:
( ABC ) А В С ,
АВС 2d 180 0 0 .

6. 7. Треугольники. Свойства дефекта треугольника

2. Если в АВС точка D ВС, то
АВС АВD АСD
Доказательство (самостоятельно).

7. 7. Треугольники. Свойства дефекта треугольника

3. Если в АВС точка В АВ, С АС и
АВС 0 , то АВ С 0 .
Доказательство (самостоятельно).

8. 7.2. Гиперболические треугольники: свойства

1. Имеют место абсолютные свойства
треугольников – все теоремы
о треугольниках, которые доказываются без
помощи аксиомы параллельных (V постулата):
1.1. Свойства равнобедренного треугольника.
1.2. Признаки равенства треугольников.
1.3. Свойства внешнего угла треугольника.
1.4. Соотношения между сторонами и углами.
1.5. Теоремы о пересечении медиан и биссектрис.

9. 7.2. Свойства треугольников в геометрии Лобачевского

2. Имеют место теоремы о
треугольниках, специфические для
геометрии Лобачевского
Теорема 4.
На плоскости Лобачевского
сумма углов любого
треугольника меньше 2d
(АВС) 2d
(7.2)

10. 7.2. Свойства треугольников в геометрии Лобачевского

Дано:
АВС
( ABC ) 2d
Доказать:
Доказательство. От противного. Пусть ( ABC ) 2d.
Случай 1.
Тогда АВС 2d ABC 2d.
=0, тогда выполняется V постулат Евклида,
( ABC ) =2d, получили противоречие.

11. 7.2. Свойства треугольников в геометрии Лобачевского

Дано:
АВС
( ABC ) 2d
Доказать:
Доказательство. От противного. Пусть ( ABC ) 2d.
Случай 2.
Тогда АВС 2d ABC 2d.
0, тогда ( ABC ) >2d
противоречие с теоремой Саккери–Лежандра (см. слайд 4).
Значит, ( ABC ) 2d
Что и требовалось доказать

12. 7.2. Свойства треугольников в геометрии Лобачевского

Следствие 1.
На плоскости Лобачевского дефект
любого треугольника есть
положительное число
(АВС) 0.
(7.3)
Следствие 2.
Сумма углов треугольника
непостоянна, т.е. не одна и та же для
всех треугольников

13. 7.3. Гиперболические четырехугольники

На плоскости Лобачевского
сумма углов выпуклого
четырехугольника меньше 4d
( ABCD ) А В С D 4d
(7.4)

14. 7.3.1. Свойства четырехугольников: Теорема 5

Дано: АВСD
Доказать:
(АВСD) 4d

15. 7.3.1. Свойства четырехугольников: Теорема 5

Доказательство.
1. Проведем
диагональ АС
2. Рассмотрим
АВС и АСD

16. 7.3.1. Свойства четырехугольников: Теорема 5

А В С D =
ВАС САD B BCA ACD D
АСD САD D BCA CAB B
( ACD ) ( ABC ) 4d
.
2 d
2 d
Что и требовалось доказать

17. 7.3. Четырехугольники Двупрямоугольники

Определение 11.
Двупрямоугольником называется
четырехугольник с двумя прямыми
углами, прилежащими к одной
стороне

18. 7.3.2. Двупрямоугольники

Двупрямоугольник
ABCD четырехугольник с
двумя прямыми
углами A и B,
прилежащими к
одной стороне АВ
АВ – основание
АD, ВС – боковые
стороны
СD – четвертая
сторона

19. 7.3.2. Двупрямоугольники

Определение 12.
Двупрямоугольник
с равными боковыми
сторонами
называется
четырехугольником
Саккери (или
Хайяма–Саккери).

20. 7.3.2. Двупрямоугольники: свойства

1. В четырехугольнике
Саккери углы при
четвертой вершине
равны и каждый из
них острый

21. 7.3.2. Двупрямоугольники: свойства

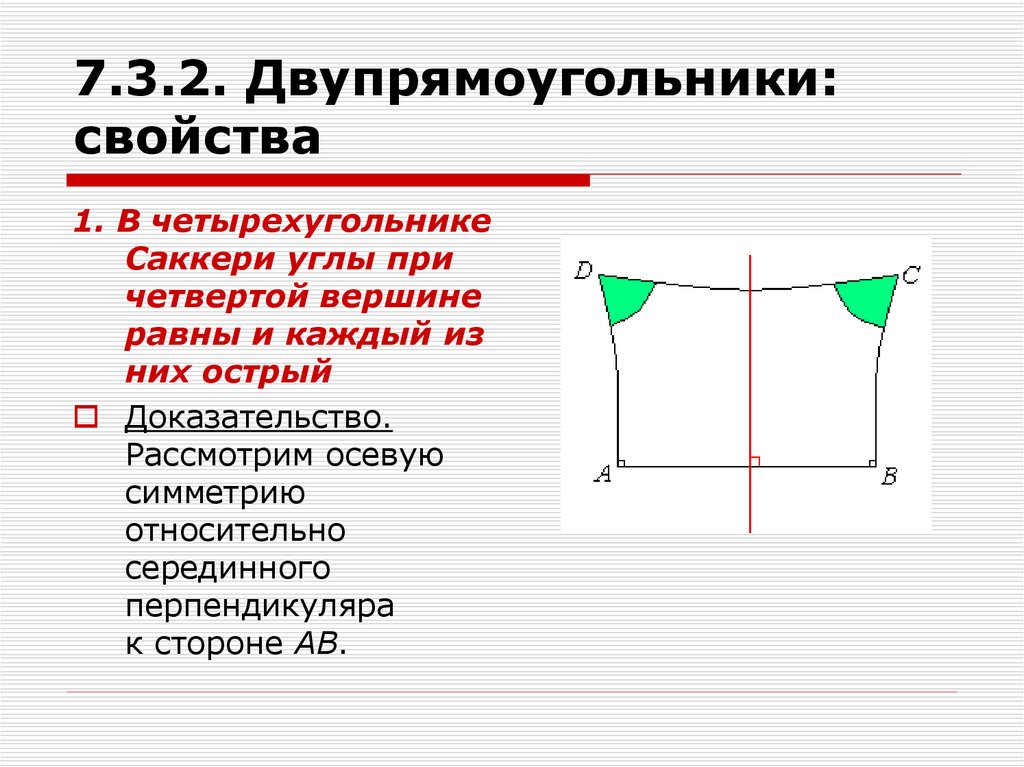
1. В четырехугольнике
Саккери углы при
четвертой вершине
равны и каждый из
них острый
Доказательство.
Рассмотрим осевую
симметрию
относительно
серединного
перпендикуляра
к стороне АВ.

22. 7.3.2. Двупрямоугольники: свойства

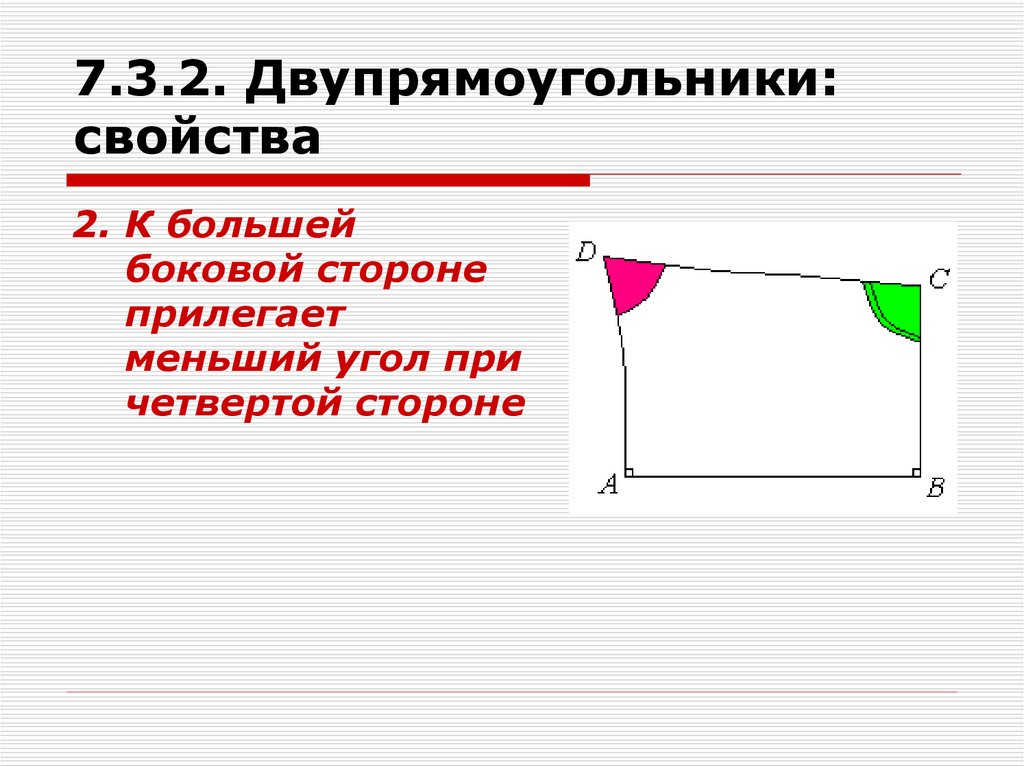
2. К большей
боковой стороне
прилегает
меньший угол при
четвертой стороне

23. 7.4. Линии: Окружность. Эквидистанта. Орицикл

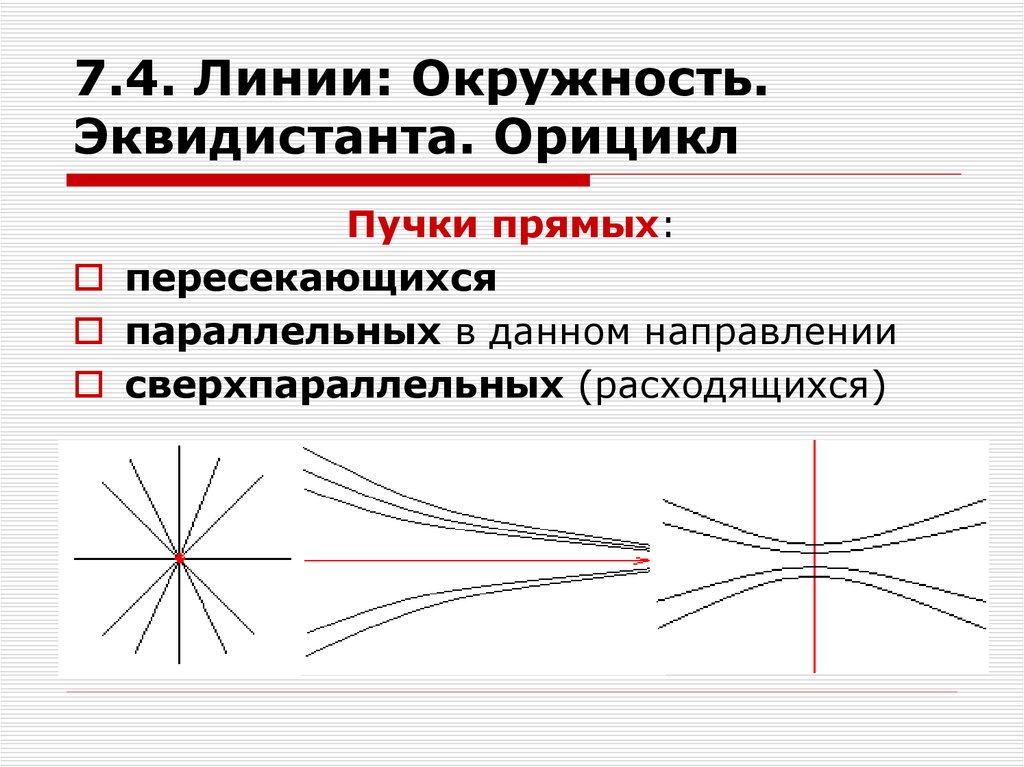
Пучки прямых:
пересекающихся
параллельных в данном направлении
сверхпараллельных (расходящихся)

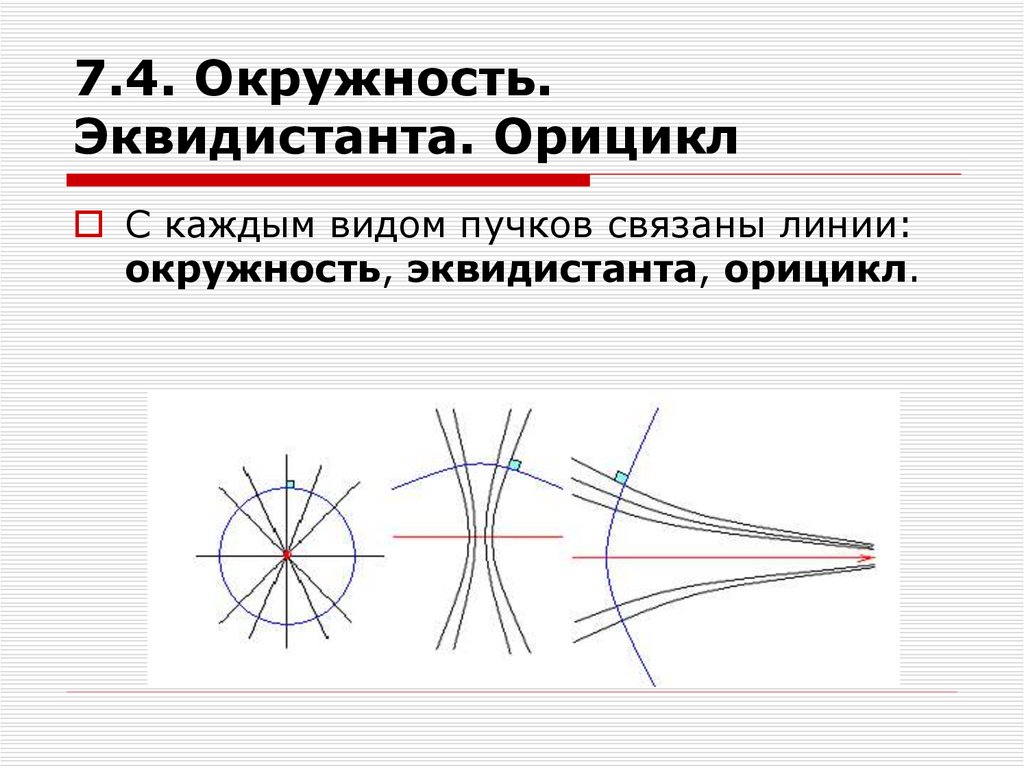
24. 7.4. Окружность. Эквидистанта. Орицикл

С каждым видом пучков связаны линии:
окружность, эквидистанта, орицикл.

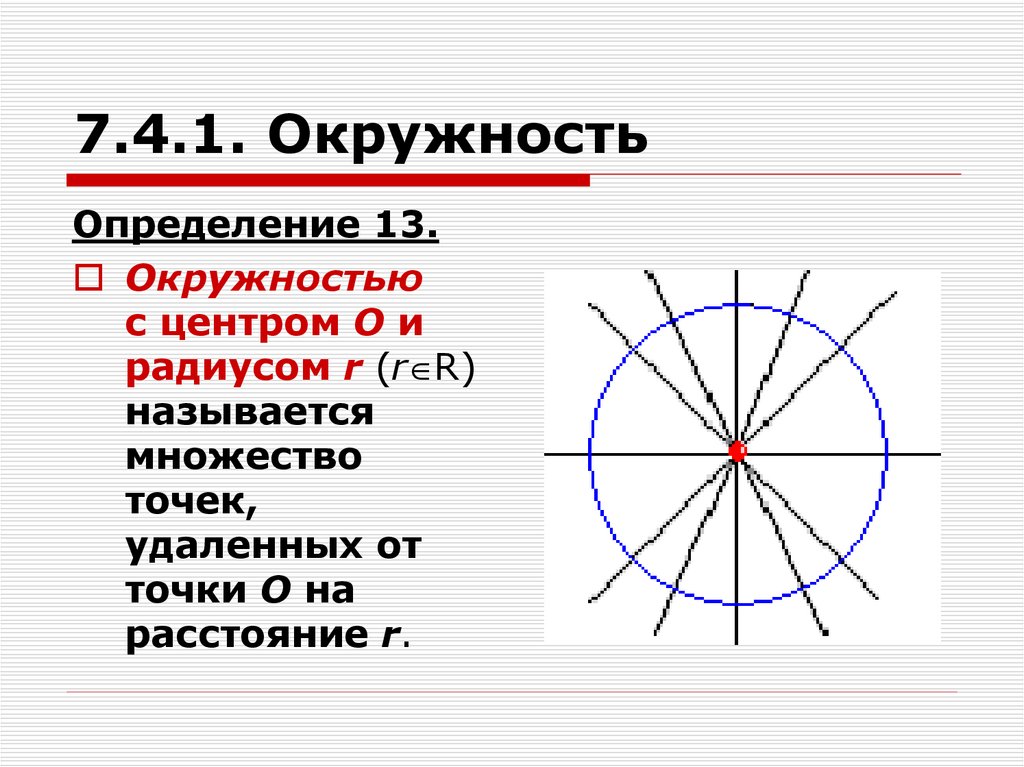
25. 7.4.1. Окружность

Определение 13.
Окружностью
с центром О и
радиусом r (r R)
называется
множество
точек,
удаленных от
точки О на
расстояние r.

26. 7.4.1. Окружность

Свойства окружности:
1. Определение абсолютной геометрии.
2. Многие теоремы об окружности
доказываются без аксиомы
параллельных, поэтому
соответствующие свойства
окружности справедливы в
геометрии Лобачевского.
3. Любая прямая пересекает
окружность не более чем в двух
точках.

27. 7.4.1. Окружность

Свойства окружности:
Рассмотрим прямые, проходящие через
центр окружности. Они образуют пучок
пересекающихся в точке О прямых.
Прямые этого пучка называют осями
окружности
4. Окружность симметрична
относительно любой своей оси.
Окружность – геометрическое место
точек, попарно симметричных
относительно пучка пересекающихся
прямых.

28. 7.4.1. Окружность

Свойства окружности:
5. В каждой точке окружности
существует касательная,
перпендикулярная оси, т.е.
окружность пересекает оси под
прямым углом.
Окружность – ортогональная траектория
пучка пересекающихся прямых с центром
в центре окружности.

29. 7.4.1. Окружность

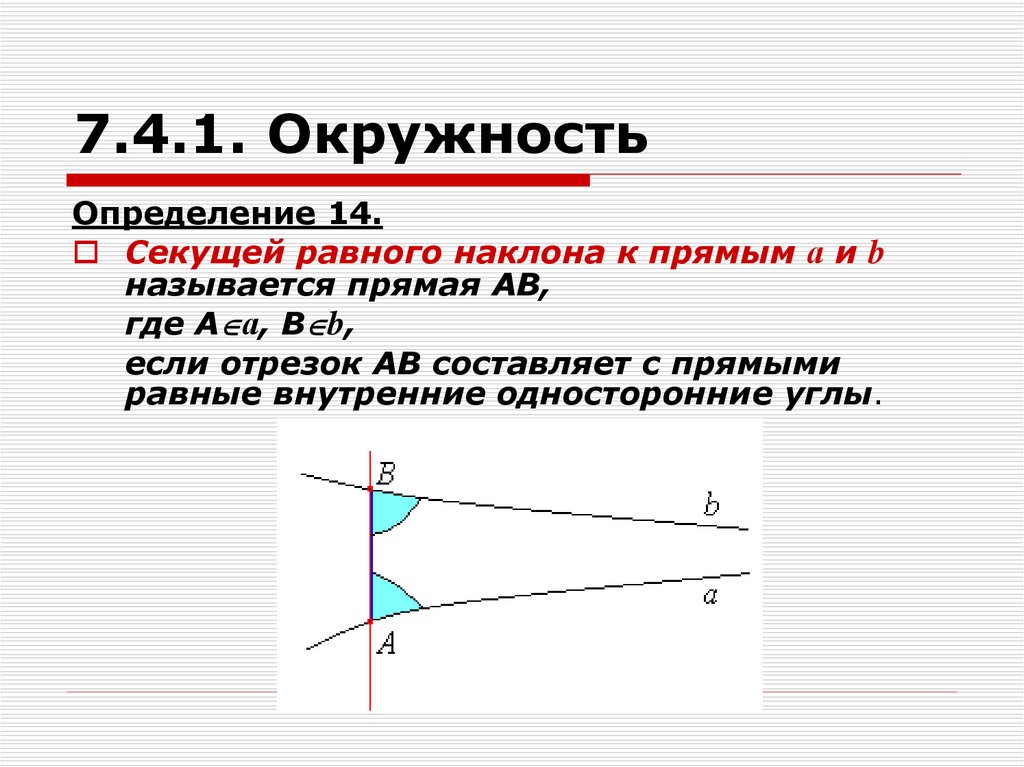
Определение 14.
Секущей равного наклона к прямым а и b
называется прямая АВ,
где А а, В b,
если отрезок АВ составляет с прямыми
равные внутренние односторонние углы.

30. 7.4.1. Окружность

6. Прямая, содержащая хорду окружности, отличную от
диаметра, является секущей равного наклона к осям,
проходящим через концы хорды.
7. Серединный перпендикуляр к хорде окружности
является ее осью симметрии.
8. Любой угол, вписанный в окружность и опирающийся
на ее диаметр, острый.
Доказательство. (самостоятельно. А.Ч.2.С.271)
9. Около треугольника можно описать окружность, если
два серединных перпендикуляра к его сторонам
пересекаются.
(дома: к свойствам сделать чертежи)

31. 7.4.2. Эквидистанта

Определение 15.
Эквидистантой называется
множество всех точек, лежащих в
одной полуплоскости с границей а и
равноудаленных от нее.

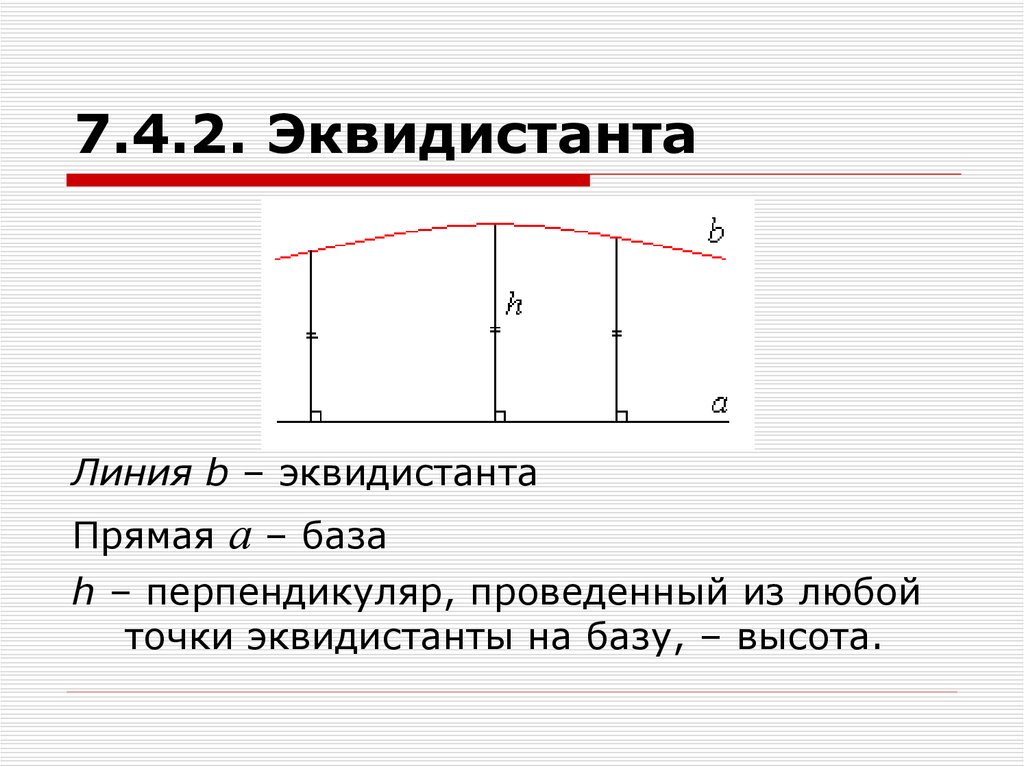
32. 7.4.2. Эквидистанта

Линия b – эквидистанта
Прямая а – база
h – перпендикуляр, проведенный из любой
точки эквидистанты на базу, – высота.

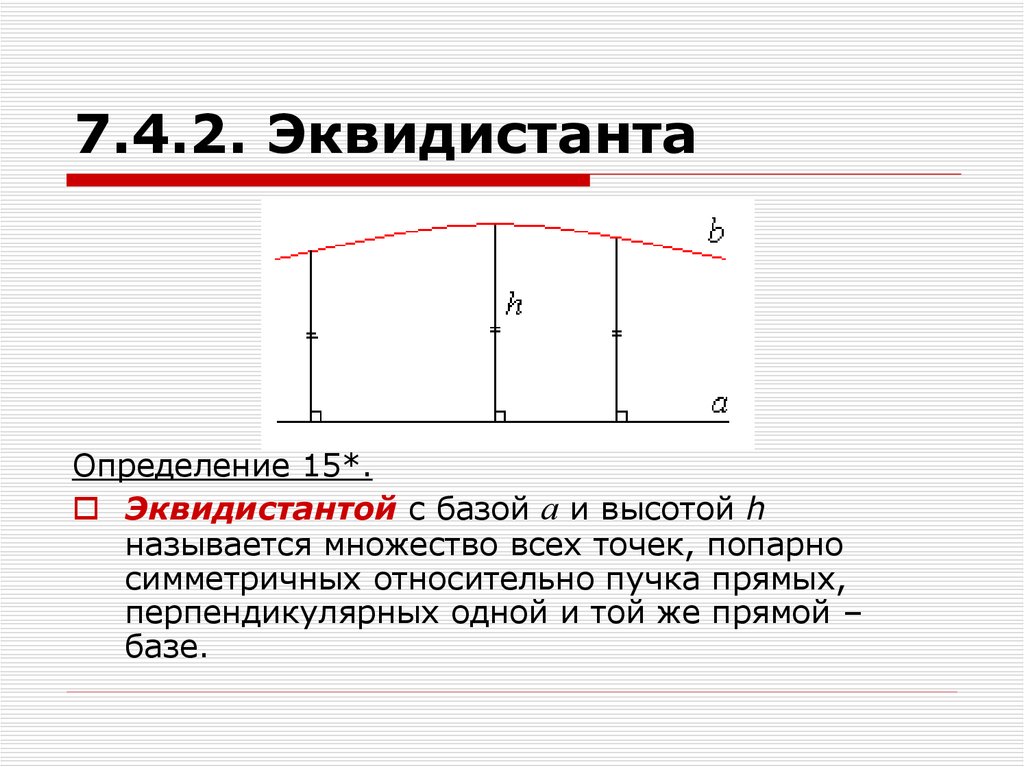
33. 7.4.2. Эквидистанта

Определение 15*.
Эквидистантой с базой а и высотой h
называется множество всех точек, попарно
симметричных относительно пучка прямых,
перпендикулярных одной и той же прямой –
базе.

34. 7.4.2. Эквидистанта

1.
Свойства эквидистанты:
Любая прямая, лежащая в плоскости эквидистанты,
пересекается с ней не более чем в двух точках.
2. Все прямые, перпендикулярные к базе эквидистанты, образуют
пучок сверхпараллельных (расходящихся) прямых.
Прямые пучка называют осями эквидистанты.
3. Эквидистанта симметрична относительно любой своей оси.
4. В каждой точке эквидистанты существует касательная,
перпендикулярная оси, проведенной через точку касания.
Эквидистанта – ортогональная траектория пучка
сверхпараллельных прямых, перпендикулярных базе
эквидистанты.

35. 7.4.2. Эквидистанта

Свойства эквидистанты:
5. Прямая, содержащая хорду эквидистанты, является
секущей равного наклона к осям, проходящим
через концы хорды.
6. Серединный перпендикуляр к хорде эквидистанты
является ее осью симметрии.
7. Около треугольника можно описать эквидистанту,
если два серединных перпендикуляра к сторонам
сверпараллельны.

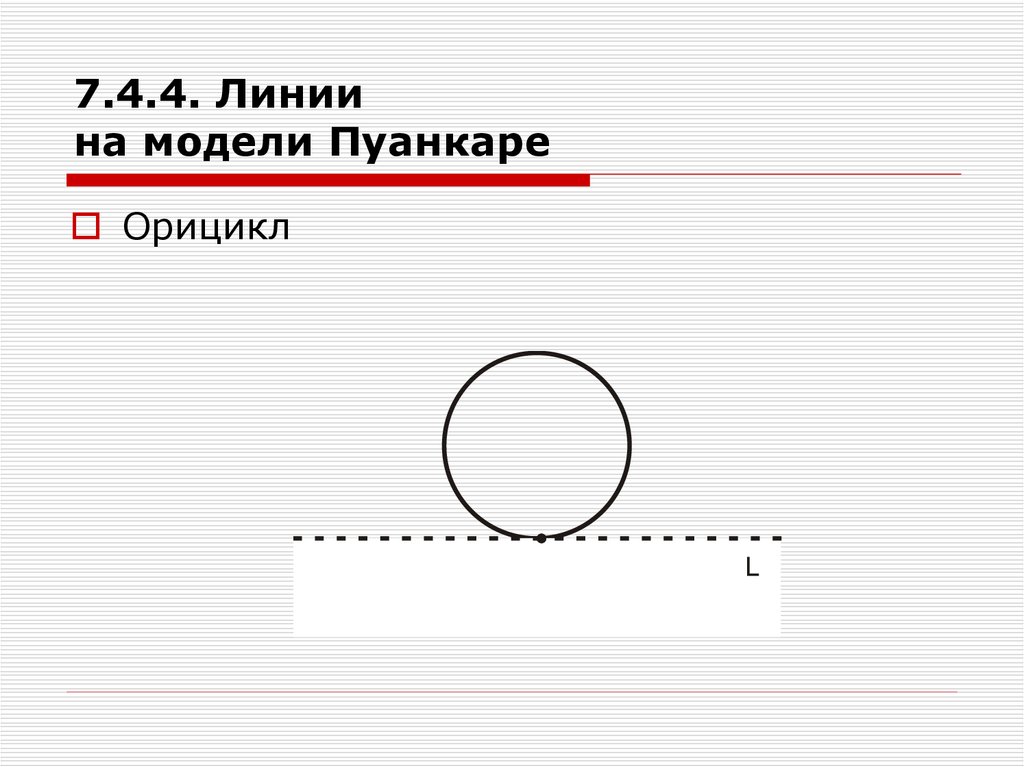
36. 7.4.3. Орицикл

Определение 16.
Орициклом называется множество точек
плоскости, попарно симметричных пучка
прямых параллельных в данном
направлении.

37. 7.4.3. Орицикл

Свойства орицикла:
1. Любая прямая, лежащая в плоскости орицикла,
пересекается с ней не более чем в двух точках.
2. Все прямые, перпендикулярные к орициклу, образуют
пучок прямых, параллельных в данном направлении.
Прямые пучка называют осями орицикла.
3. Орицикл симметричен относительно любой своей оси.
4. В каждой точке орицикла существует касательная,
перпендикулярная оси, проведенной через точку
касания.
Орицикл – ортогональная траектория пучка его
параллельных осей.

38. 7.4.3. Орицикл

Свойства орицикла:
5. Прямая, содержащая хорду орицикла,
является секущей равного наклона к осям,
проходящим через концы хорды.
6. Серединный перпендикуляр к хорде орицикла
является ее осью симметрии.
7. Любые два орицикла равны.
8. Около треугольника можно описать орицикл,
если два серединных перпендикуляра к
сторонам параллельны в некотором
направлении.

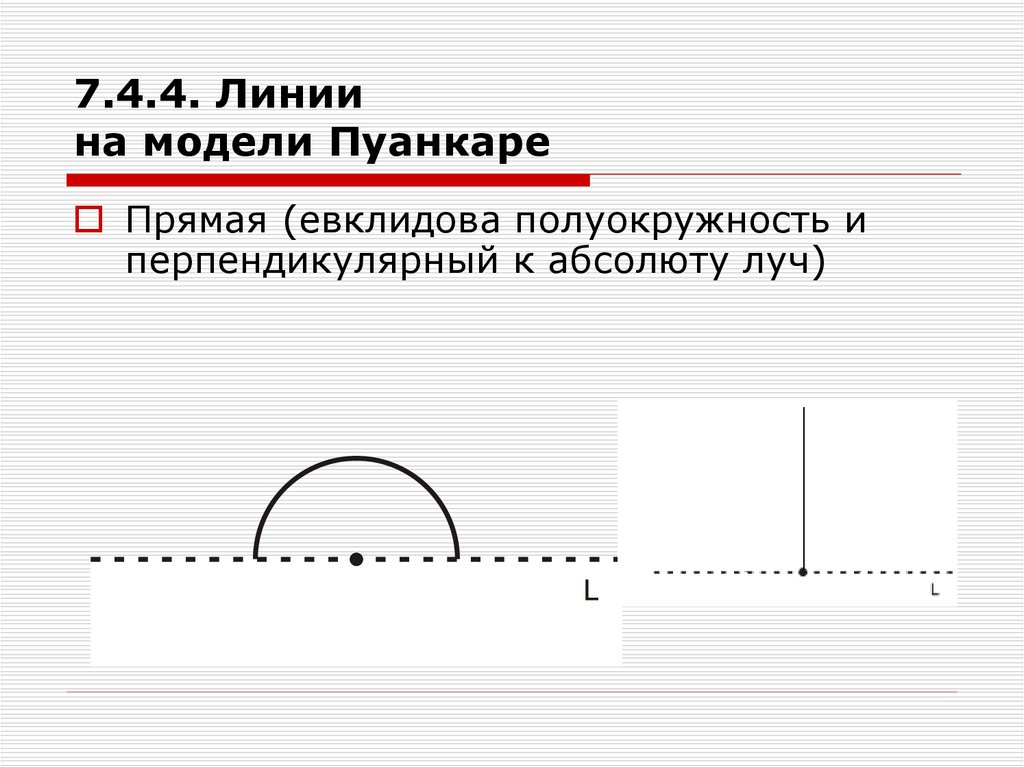
39. 7.4.4. Линии на модели Пуанкаре

Прямая (евклидова полуокружность и
перпендикулярный к абсолюту луч)

40. 7.4.4. Линии на модели Пуанкаре

Окружность

41. 7.4.4. Линии на модели Пуанкаре

Эквидистанта

42. 7.4.4. Линии на модели Пуанкаре

Орицикл