Отличие геометрии Лобачевского от геометрии Евклида

1.

Министерство образования Нижегородской области
Государственное бюджетное профессиональное образовательное учреждение
«Павловский техникум народных художественных промыслов России»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
«ПАВЛОВСКИЙ ТЕХНИКУМ НАРОДНЫХ ХУДОЖЕСТВЕННЫХ ПРОМЫСЛОВ
РОССИИ»
Индивидуальный проект
Тема: «Отличие геометрии Лобачевского
от геометрии Евклида»
ИНДИВИДУАЛЬНЫЙ
ПРОЕКТ
ТЕМА: «ОТЛИЧИЕ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
ОТ ГЕОМЕТРИИ ЕВКЛИДА»
Автор: Кондрашева Дарья Борисовна,
Автор:I Кондрашева
Дарья Борисовна,
обучающаяся
курса по специальности
обучающаяся I курса по специальности
54.02.02
Декоративно-прикладное
54.02.02
Декоративно-прикладное
искусство
и
народные
промыслы (по
искусство и народные
промыслы
(по
видам)
видам)
Руководитель: Клюкина
О. В.,
преподаватель
математики
и
Руководитель:
Клюкина
О.
В.,
естествознания ГБПОУ ПТ НХП РФ
преподаватель математики
ГБПОУ ПТ НХП РФ

2.

Геометрия – это раздел математики,
изучающий
пространственные
структуры
Геометрия –это математики, изучающий пространственные структуры и
и отношения,
их
обобщения.
отношения, а такжеаихтакже
обобщения.
Геометрия
как систематическая наука
появилась в Древней Греции, её аксиоматические построения описаны в
«Началах» Евклида.
Геометрия как систематическая наука
появилась в Древней Греции,
её аксиоматические построения описаны в
«Началах» Евклида.

3.

Биография Евклида
Евклид (365 - 300 до н. э.) – известный
древнегреческий математик
Родился в Афинах .
Был учеником Платона.
Расцвет его деятельности пришёлся на время
царствования в Египте Птолемея I (IV в. до н. э.)
Основал математическую школу,
Создал для своих учеников фундаментальный труд по
геометрии под общим названием «Начала»,
в котором изложил основы планиметрии,
стереометрии, теории чисел, алгебры, описаны
методы определения площадей и объёмов и т. д.
«Начала» состоят из 13 книг.
Это был самый популярный письменный памятник
древности после Библии.
Умер Евклид предположительно в Александрии.

4.

Биография Н.И Лобачевского
Николай Иванович Лобачевский (1792-1856) - известный математик,
создатель неевклидовой геометрии.
Родился 1 декабря 1792 г. в Нижнем Новгороде.
В семилетнем возрасте остался без отца и мать вместе с тремя сыновьями переехала в
Казань, где окончил Казанский университет.
В 1814 г. приступил к чтению лекций по теории чисел.
Трудился над созданием неевклидовой геометрии с перерывами не менее 20 лет.
Его первое публичное сообщение по этой теме было сделано на физикоматематическом факультете Казанского университета в 1826 году и затем представлено
в статье «Новые начала геометрии с полной теорией
параллельных»
(«Учёные записки Казанского университета», 1835 г.).
Европейские учёные узнали о работах Лобачевского в 1840 г.,
в 1842 он был избран членом-корреспондентом Гёттингенского
научного общества.
В Казанском университете Лобачевский читал лекции
по астрономии и проводил астрономические наблюдения.

5.

В 1883-1886 гг. Казанский университет издал «Полное
собрание сочинений по геометрии Лобачевского».
В 1893 г. в честь столетия
со дня рождения Лобачевского ему
воздвигли памятник в Казани на
собранные по международной
подписке средства. В 1895 г. Казанское
физико-математическое общество
учредило премию имени Лобачевского
за выдающиеся работы в области
геометрии. Эту награду и сейчас
присуждает Российская академия наук

6.

Основные периоды развития математики
Андрей Николаевич Колмогоров (1903-1987) – крупнейший
современный математик, академик, известный своими
выдающимися трудами в различных областях математики –
выделил 4 периода в развитии математики:
I период зарождения математики, который длился до VI-V вв. до н.э.
II период – период элементарной математики
(период математики постоянных величин).
Длился с VI-V вв. до н.э. по XVII в. н.э.
III период – период математики переменных величин, изучающей
процессы движения, изменения, развития. Длился с XVII по XIX в. н.э.
IV период – период современной математики
(математики математических структур).
Длится с середины XIX в. по настоящее время.

7.

Постулаты Евклида –
утверждения, принимаемые без доказательств
Евклид – автор первого дошедшего до нас строгого логического построения геометрии.
Определения: 1. Точка есть то, что не имеет частей 2. Линия есть длина без ширины. 3. Границы линии суть точки
ПОСТУЛАТЫ:
Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.
И чтобы каждую прямую можно было неопределенно продолжить. И чтобы все прямые углы были равны.
И чтобы из любого центра можно было описать окружность любым радиусом.
И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними
Односторонние внутренние углы, сумма которых меньше двух прямых, эти прямые пересекались
с той стороны, с которой эта сумма меньше двух прямых.
АКСИОМЫ:
Равные порознь третьему равны между собой.
И если от равных отнимем равные, то получим равные.
И совмещающиеся равны.
И если к неравным прибавим равные, то получим неравные.
И целое больше части.
И если удвоим равные, то получим равные.
И две прямые не могут заключать пространства
И если к ним прибавим равные, то получим равные.
И половины равных равны между собой.

8.

ПОНЯТИЕ ОБ АКСИОМАТИЧЕСКОМ МЕТОДЕ
1. Вводятся в рассмотрение первичные
(неопределяемые) объекты.
2. Свойства этих объектов, их взаимосвязи формулируются
в специальных предложениях, называемых аксиомами,
которые принимаются без доказательства.
3.Формируется понятийный аппарат
(даются определения новым понятиям)
на основе первичных и ранее
определенных понятий.
4. Устанавливается истинность
новых предложений,
то есть доказываются теоремы,
на основе аксиом
и ранее доказанных теорем.

9.

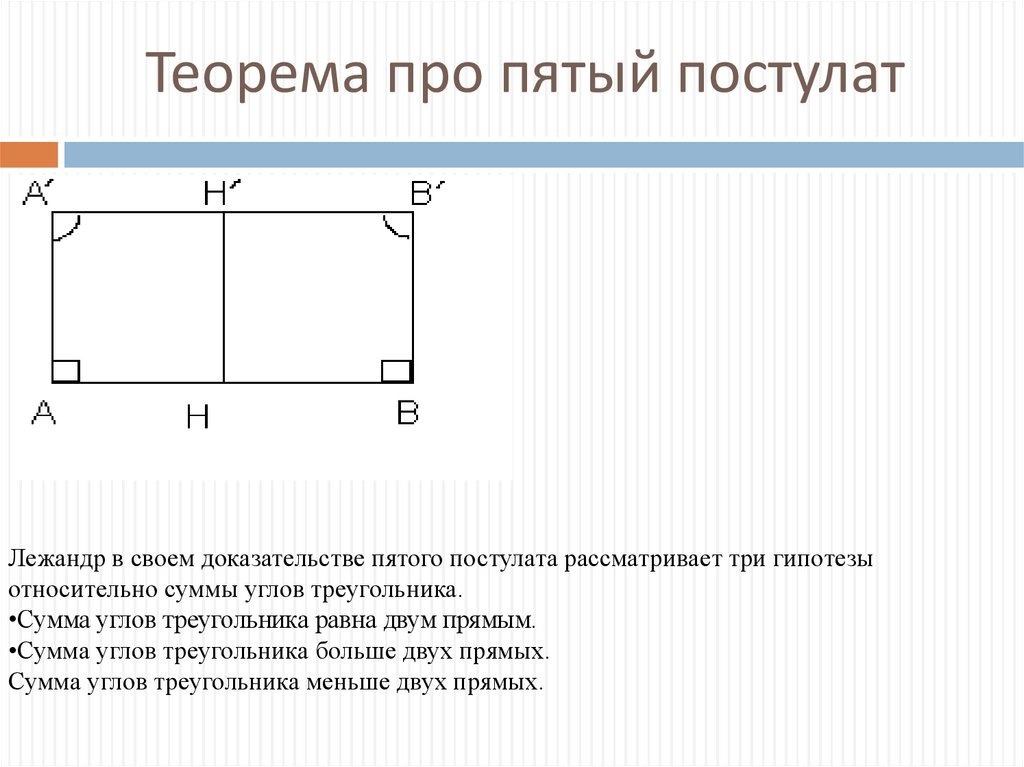
Теорема про пятый постулат
Лежандр в своем доказательстве пятого постулата рассматривает три гипотезы
относительно суммы углов треугольника.
•Сумма углов треугольника равна двум прямым.
•Сумма углов треугольника больше двух прямых.
Сумма углов треугольника меньше двух прямых.

10.

АКСИОМАТИКА ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
Пятый постулат называется постулатом о параллельных.
Относительная сложность и неинтуитивность его
формулировки вызывала ощущение его вторичности и
порождала попытки вывести его как теорему из остальных
постулатов Евклида.
Возникало понимание о том, что возможно построение
теории, основанной на противоположном постулате:
Лобачевский в работе «О началах геометрии» (1829) заявили,
что V постулат не может быть доказан на основе других
посылок евклидовой геометрии, и что допущение постулата,
противоположного постулату Евклида, позволяет построить
геометрию столь же содержательную, как и евклидова, и
свободную от противоречий.
Лобачевский доказал, что пятый постулат не зависит от
остальных предложений и доказать его нельзя.

11.

ОТЛИЧИЕ ГЕОМЕТРИИ ЕВКЛИДА
ОТ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих её и находящихся с
ней в одной плоскости; среди них есть две крайние b, b`, которые и называются параллельными прямой а в смысле
Лобачевского.
В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) а общий конец
(который по определению модели исключается, так что эти прямые не имеют общих точек). Угол ее между прямой b (или b`)
и перпендикуляром из О на а - так называемый угол параллельности - по мере удаления точки О от прямой убывает от 90° до
0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно
видеть непосредственно). Параллель b с одной стороны (а b` с противоположной) асимптотически приближается к а, а с
другой - бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не
виден).
Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно
восстановить перпендикуляры, которые не достигают другой прямой.
Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.
Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной
окружностью, или орициклом.
Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность - предельная сфера, или
орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода
формул тригонометрии.
Длина окружности не пропорциональна радиусу, а растет быстрее.
Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой
области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место
евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от p; чем меньше
окружность, тем меньше отношение её длины к радиусу отличается от 2p, и т. п. Уменьшение области формально
равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы Лобачевского
геометрия переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай
Лобачевского геометрии

12.

Спасибо за внимание