Similar presentations:
Лобачевский и его геометрия
1.
2. Евклид (III век до н. э.) Древнегреческий математик, автор первого трактата по геометрии «Начала» (в 13 книгах).
В основе всей геометрии греческогоматематика Евклида лежало несколько простых
первоначальных утверждений (аксиом),
которые принимались за истинные без
доказательств. Из аксиом путем доказательств
выводились более сложные утверждения, из
тех выводились еще более сложные.
Особый интерес математиков всегда вызывала
пятая аксиома о параллельных прямых. В
отличие от остальных аксиом элементарной
геометрии, аксиома параллельных не обладает
свойством непосредственной очевидности.
Поэтому на всем протяжении истории
геометрии имели место попытки доказать
аксиому параллельных.
3.
Любая теория современной науки считается единственноверной, пока не создана следующая. Невозможность
доказать некоторое геометрическое утверждение средствами
евклидовой геометрии послужило поводом построения
другой геометрии, которая также является верной.
Был мудрым Евклид,
Но его параллели,
Как будто бы вечные сваи легли.
И мысли его, что как стрелы летели,
Всегда оставались в пределах Земли.
А там, во вселенной, другие законы,
Там точками служат иные тела.
И там параллельных лучей миллионы
Природа сквозь Марс, может быть, провела.
4. Видите движение на этой картинке?
5. Эксперимент «Иллюзии зрения»
На рисунке буквырасположены
параллельно (стоят
прямо) или нет?
1
На рисунке изображена
спираль или
несколько
окружностей?
2
6. Эксперимент «Иллюзии зрения»
ВЫВОД:В геометрии истинность каждого
утверждения необходимо доказывать, нельзя полагаться
только на наблюдения.
7.
Все! Перечеркнуты “Начала”.Довольно мысль на них скучала,
Хоть прав почти во всем Евклид,
Но быть не вечно постоянству:
И плоскость свернута в
пространство,
И мир
Иной имеет вид...
Заменив V постулат евклидовой геометрии на аксиому,
Лобачевский пришел к выводу, что можно построить другую
геометрию, отличную от евклидовой.
8. Николай Иванович Лобачевский (1792 – 1856 гг.)
Дата рождения:Место рождения:
Дата смерти:
Место смерти:
1 (12) декабря 1792[1]
Нижний Новгород[2]
24 февраля (7 марта) 1856[1][3](63 года)
Казань, Казанская
губерния, Российская империя[2]
Страна:
Научная сфера:
Российская империя
математика
Место работы:
Казанский университет
Альма-матер:
Казанский университет
Научный
Мартин Бартельс
руководитель:
Известные
ученики:
И. А. Больцани,
Н. Н. Зинин,
А. Ф. Попов,
Э. П. Янишевский
Известен как:
Один из создателей неевклидовой
геометрии
Награды
и премии:
Подпись:
9.
7 февраля 1826 годаЛобачевский
представил для
напечатания в
Записках физикоматематического
отделения сочинение:
«Сжатое изложение
начал геометрии со
строгим
доказательством
теоремы о
параллельных» (на
французском языке)
«Через точку, не
лежащую на данной
прямой, проходят по
крайней мере две
прямые, лежащие с
данной прямой в
одной плоскости и не
пересекающие её»
10. «Чем отличается геометрия Лобачевского от геометрии Евклида?»
Евклидова аксиомао параллельных:
через точку, не лежащую на
данной прямой, проходит
только одна прямая, лежащая
с данной прямой в одной
плоскости и не пересекающая
её.
Аксиома
Лобачевского
о параллельных:
через точку, не лежащую на
данной прямой, проходят по
крайней мере две прямые,
лежащие с данной прямой в
одной плоскости и не
пересекающие её.
ВЫВОД: Геометрия Лобачевского отличается от
евклидовой лишь в одной аксиоме — пятой.
11.
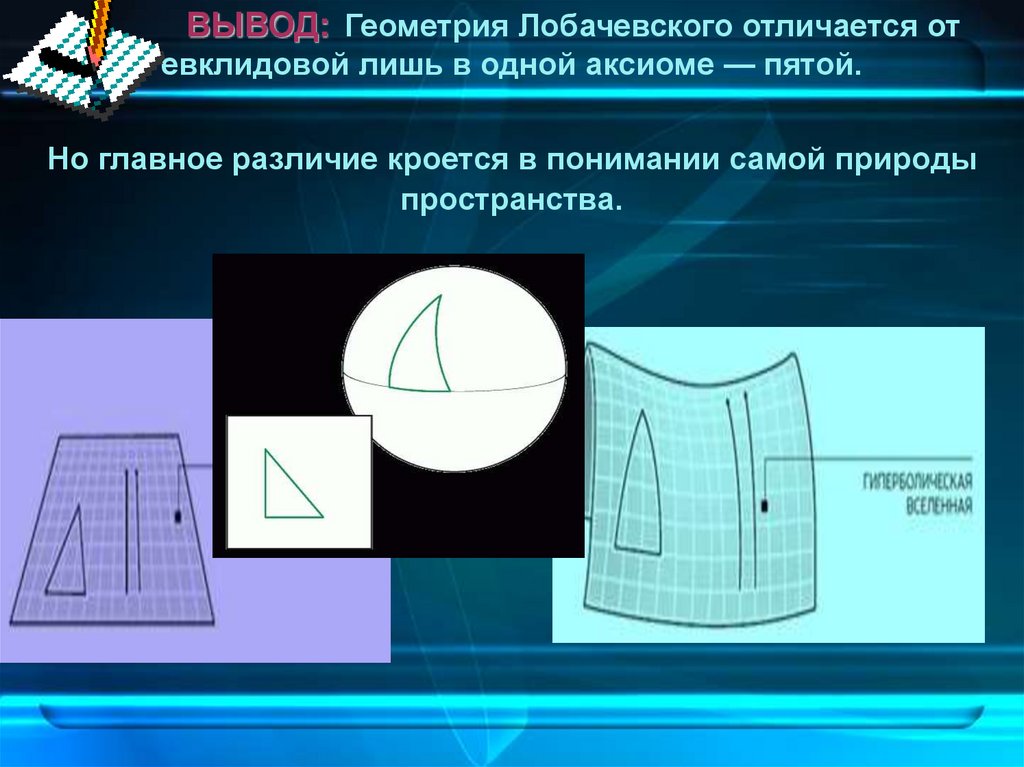
ВЫВОД: Геометрия Лобачевского отличается отевклидовой лишь в одной аксиоме — пятой.
Но главное различие кроется в понимании самой природы
пространства.
12.
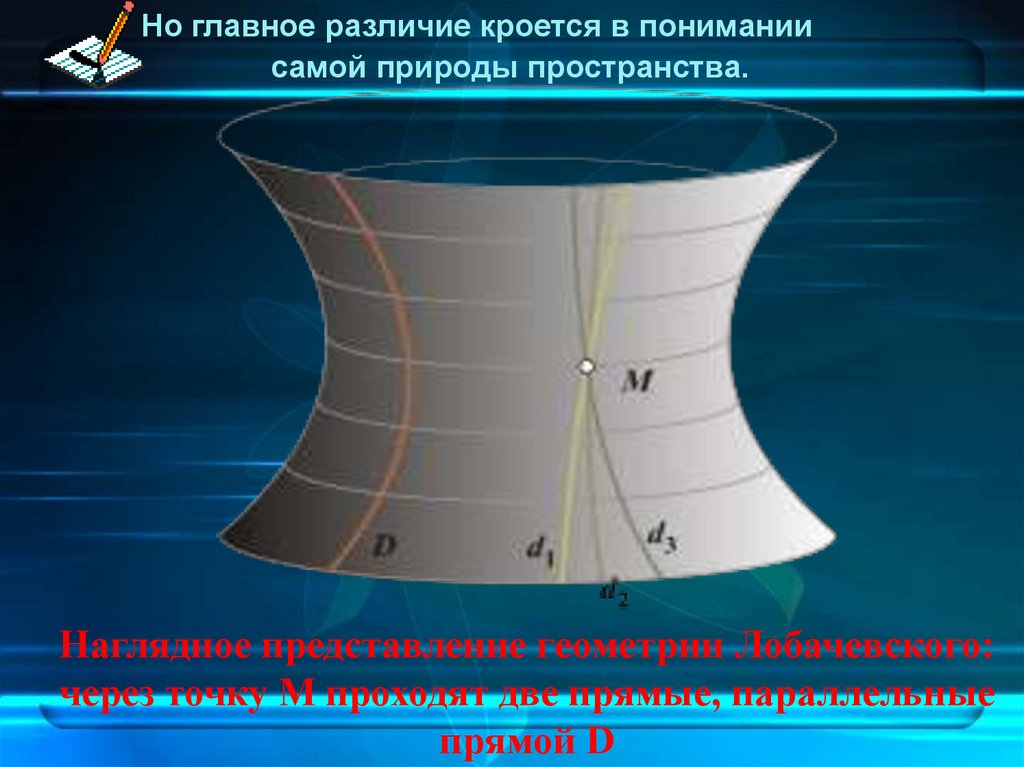
Но главное различие кроется в пониманиисамой природы пространства.
Наглядное представление геометрии Лобачевского:
через точку M проходят две прямые, параллельные
прямой D
13.
Однако научные идеиЛобачевского не были
поняты
современниками. Его
труд «О началах
геометрии»,
представленный в 1832
году советом
университета в
Академию наук,
получил у М. В.
Остроградского
отрицательную оценку
14.
Но Лобачевский несдаётся.
В 1835—1838 он
публикует в «Учёных
записках» статьи о
«воображаемой
геометрии», а затем
выходит наиболее
полная из его работ
«Новые начала
геометрии с полной
теорией
параллельных»
15. Выводы
Как показали исследования, геометрияЛобачевского (в то числе и 5-ый
постулат) совершенно верна, если ее
рассматривать не на плоскости, а на
поверхности гиперболического
параболоида (вогнутой поверхности,
напоминающей седло).
16. Выводы
Любая теория современной наукисчитается единственно верной, пока не
создана следующая. Это своеобразная
аксиома развития науки.













 mathematics
mathematics








