Similar presentations:
Кинематический анализ расчётных схем сооружений. Лекция №2
1.
СТРОИТЕЛЬНАЯ МЕХАНИКАЧасть 1
Статически определимые системы
Лекция №2
Кинематический анализ
расчётных схем
сооружений
2.
Кинематическийанализ
это исследование расчётной схемы
сооружения (системы), выполняемое
до начала расчёта с целью определения
кинематического качества системы
(геометрической неизменяемости, мгновенной
изменяемости или
геометрической изменяемости), а в случае
геометрической неизменяемости системы – также
для выявления ее статической определимости
или неопределимости.
3. Основные понятия кинематического анализа
Диск–часть системы (один или несколько
соединённых друг с другом элементов),
форма и размеры которой могут изменяться
только вследствие деформации материала.
С в я з и (механические) –
ограничения на перемещения
(линейные и/или угловые) точек или сечений
элементов системы, а также устройства,
технически реализующие эти ограничения.
Степени свободы–
независимые геометрические параметры,
полностью определяющие положение
всех точек диска или системы в целом
при их допустимых перемещениях.
4.
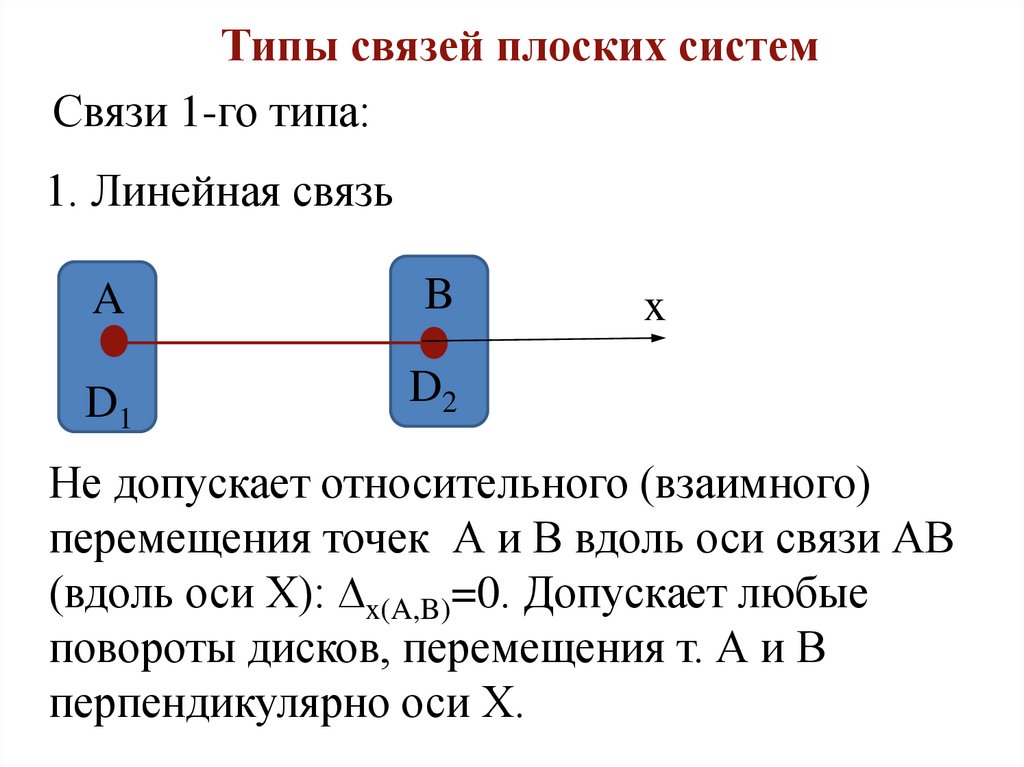
Типы связей плоских системСвязи 1-го типа:
1. Линейная связь
A
B
D1
D2
x
Не допускает относительного (взаимного)
перемещения точек А и В вдоль оси связи АВ
(вдоль оси Х): ∆x(A,B)=0. Допускает любые
повороты дисков, перемещения т. А и В
перпендикулярно оси Х.
5.
BA
D1
R
D2
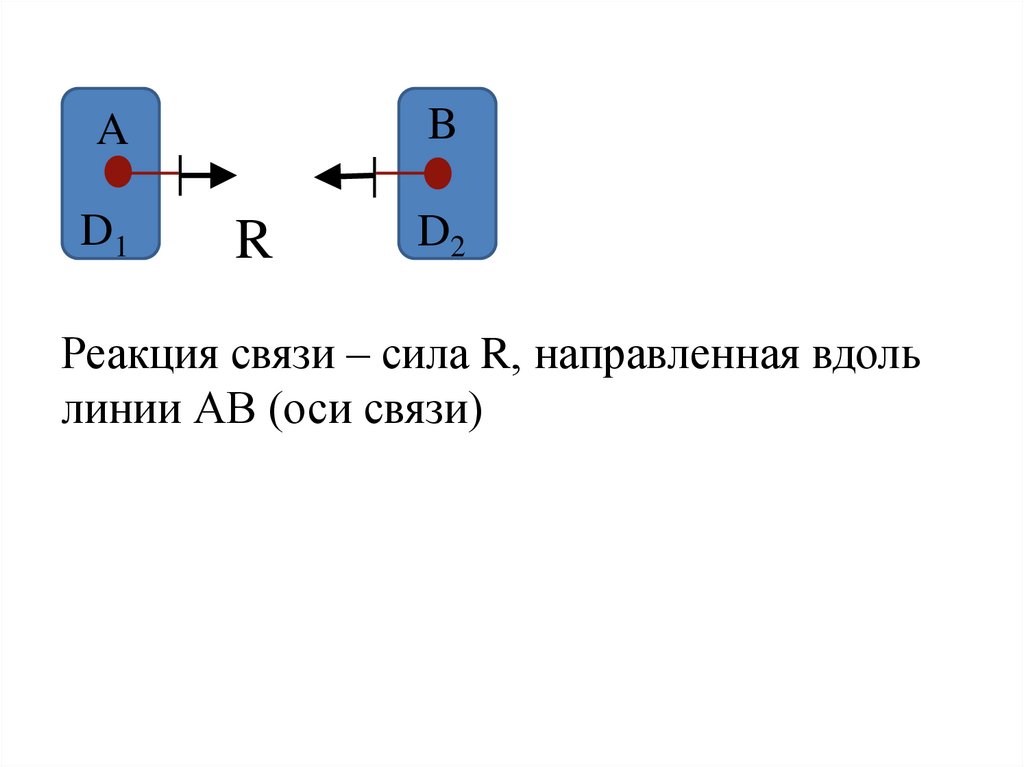
Реакция связи – сила R, направленная вдоль
линии АВ (оси связи)
6.
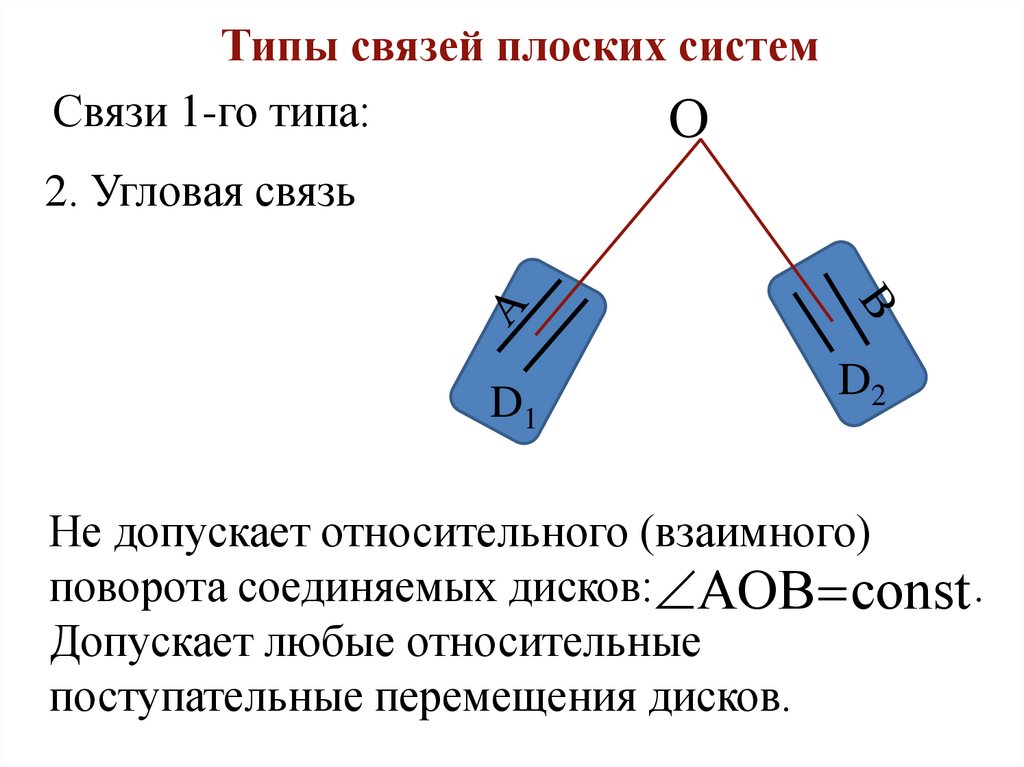
Типы связей плоских системСвязи 1-го типа:
О
2. Угловая связь
D1
D2
Не допускает относительного (взаимного)
поворота соединяемых дисков: АОВ const .
Допускает любые относительные
поступательные перемещения дисков.
7.
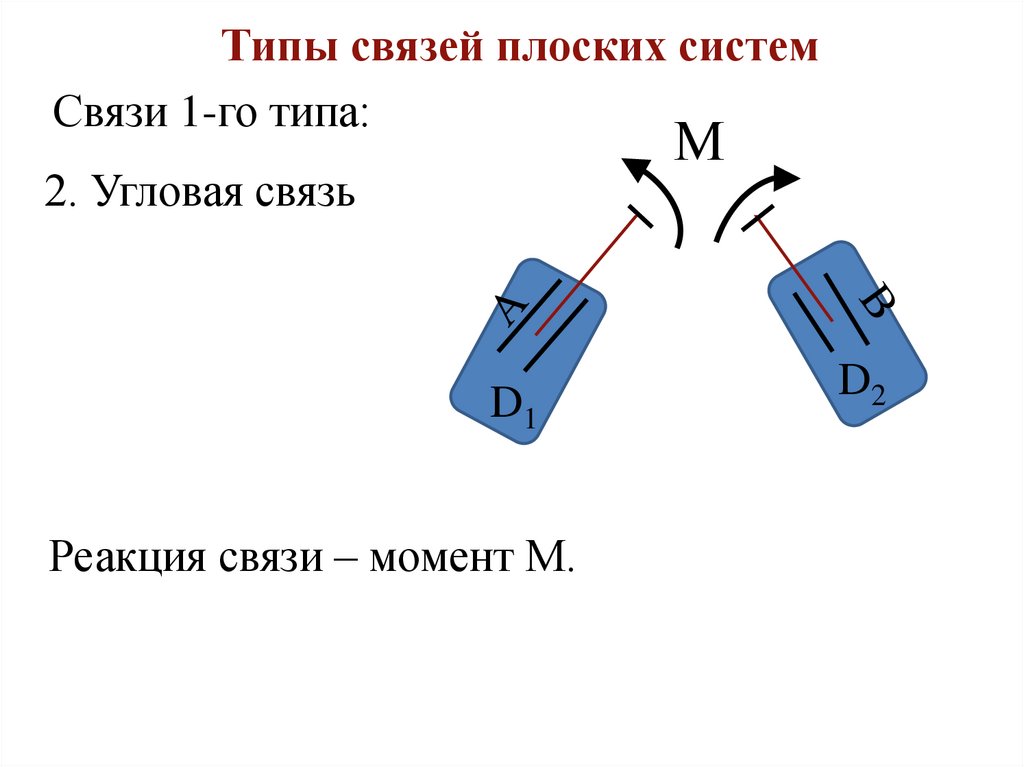
Типы связей плоских системСвязи 1-го типа:
О
М
2. Угловая связь
D1
Реакция связи – момент М.
D2
8.
Типы связей плоских системСвязи 2-го типа (шарнир):
2. Цилиндрический
шарнир
С
Не допускает относительного
D1
(взаимного)линейного
перемещения точек С1 и С2 дисков
D1и D2, совпадающих с шарниром С по
любому направлению. Не препятствует любым
поворотам дисков вокруг шарнира С.
9.
Типы связей плоских системVC1
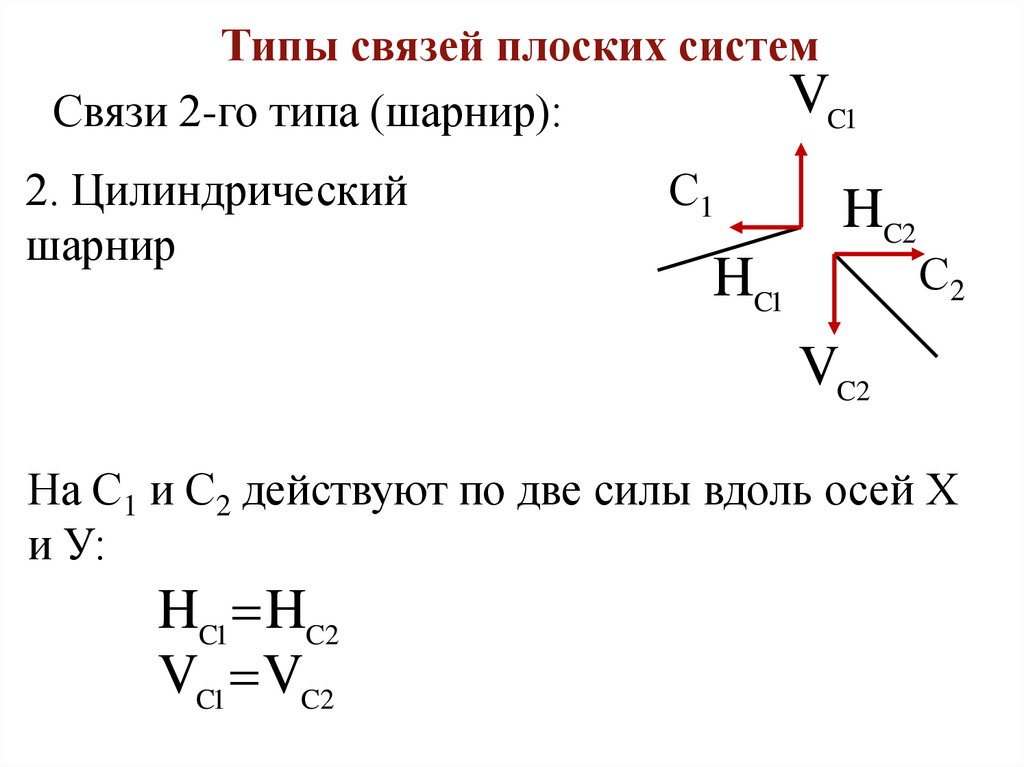
Связи 2-го типа (шарнир):
2. Цилиндрический
шарнир
С1
HC2
HC1
С2
VC2
На С1 и С2 действуют по две силы вдоль осей Х
и У:
HC1 HC2
VC1 VC2
10.
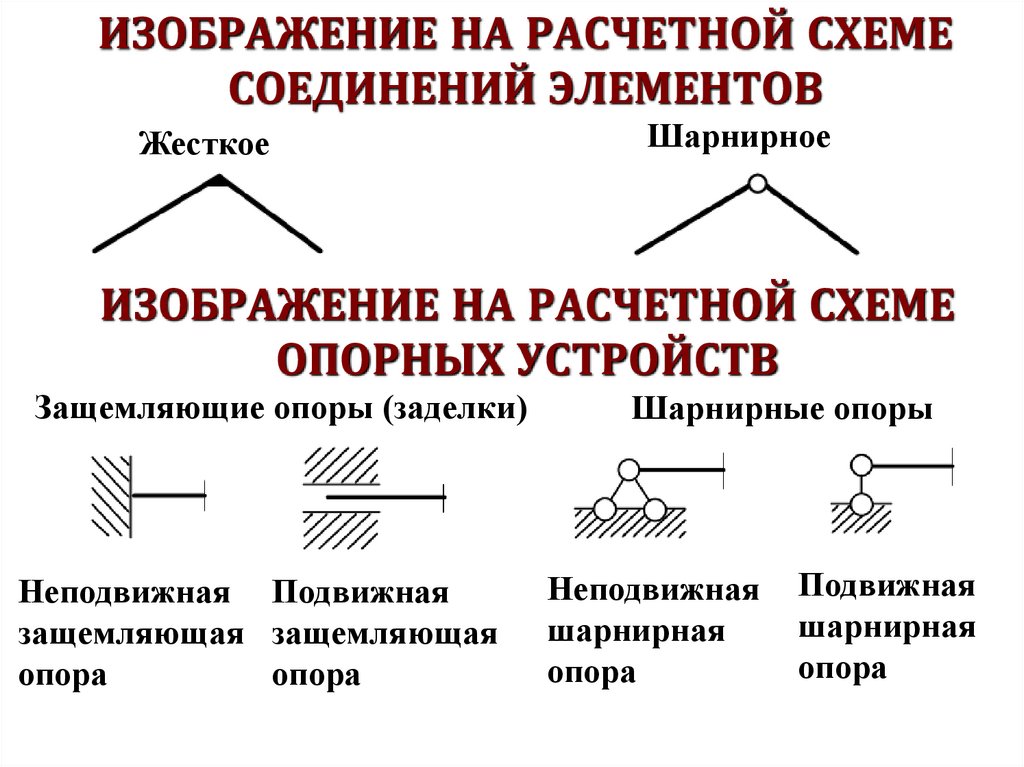
ИЗОБРАЖЕНИЕ НА РАСЧЕТНОЙ СХЕМЕСОЕДИНЕНИЙ ЭЛЕМЕНТОВ
Жесткое
Шарнирное
ИЗОБРАЖЕНИЕ НА РАСЧЕТНОЙ СХЕМЕ
ОПОРНЫХ УСТРОЙСТВ
Защемляющие опоры (заделки)
Неподвижная Подвижная
защемляющая защемляющая
опора
опора
Шарнирные опоры
Неподвижная
шарнирная
опора
Подвижная
шарнирная
опора
11.
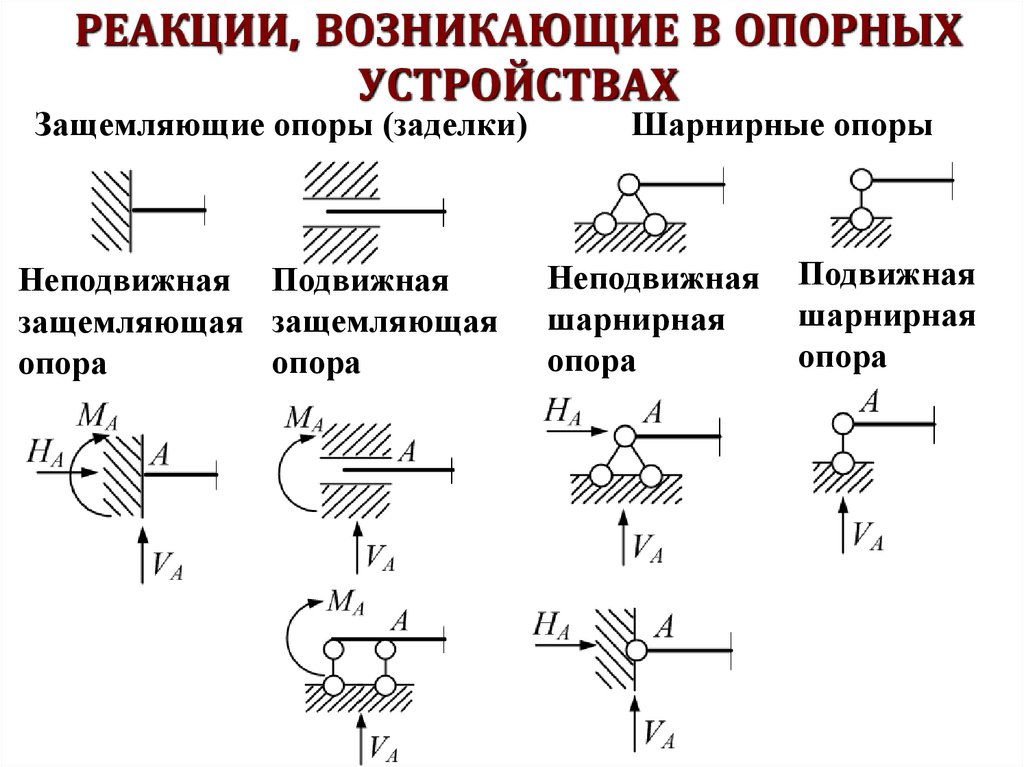
РЕАКЦИИ, ВОЗНИКАЮЩИЕ В ОПОРНЫХУСТРОЙСТВАХ
Защемляющие опоры (заделки)
Неподвижная Подвижная
защемляющая защемляющая
опора
опора
Шарнирные опоры
Неподвижная
шарнирная
опора
Подвижная
шарнирная
опора
12. Степени свободы
уНесвязанный диск
в пространстве имеет шесть
степеней свободы:
координаты xOD , yO D и zOD
yD
D
zD
OD
D
некоторой точки OD диска –
начала его локальной (собственной) системы координат
и трёх углов D, D и D
между глобальными и
локальными осями.
xD
yOD
O
z OD
xOD
z
D
x
В плоскости диск обладает тремя степенями свободы – это
координаты xOD , yOD и угол D . Точка в пространстве имеет три
степени свободы – xA, yA и zA , а в плоскости – две (xA и yA).
у
у
yD
xD
A
D
yOD
OD
yA
O
O
xOD
x
zA
x
z
xA
13.
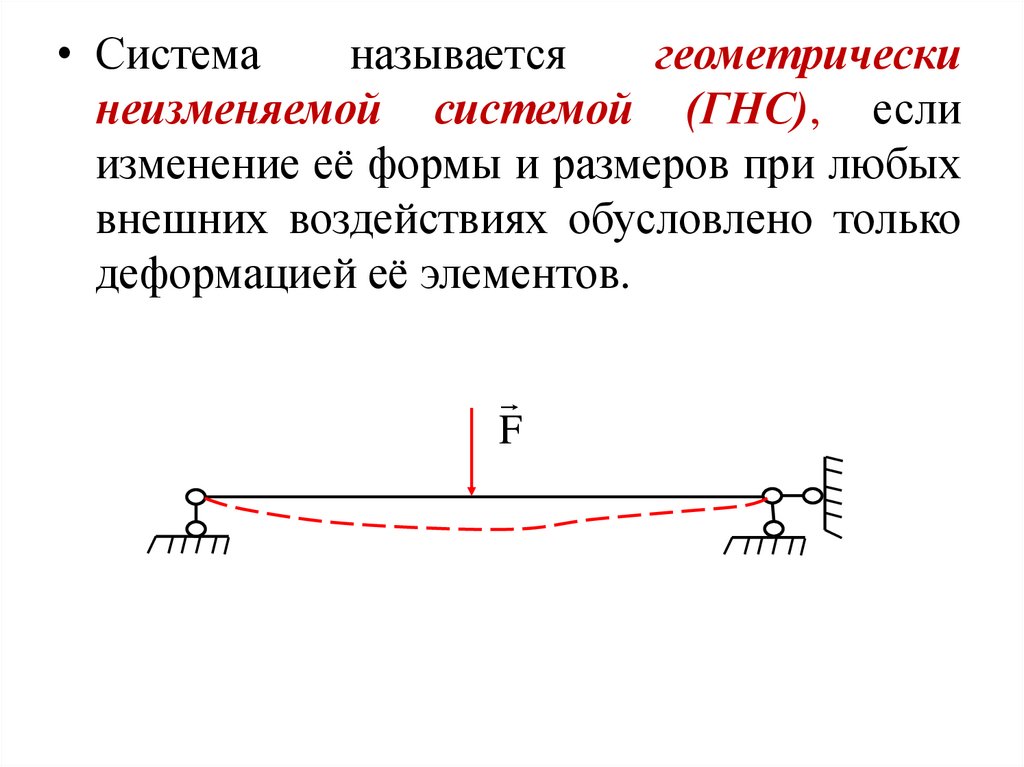
• Системаназывается
геометрически
неизменяемой системой (ГНС), если
изменение её формы и размеров при любых
внешних воздействиях обусловлено только
деформацией её элементов.
F
14.
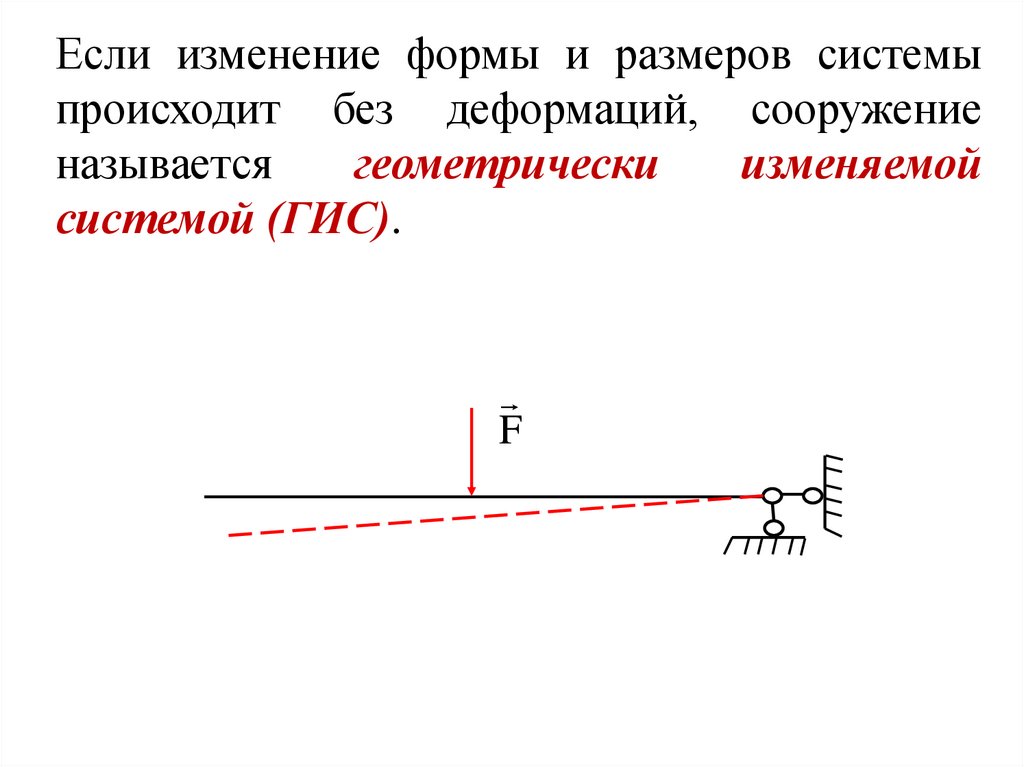
Если изменение формы и размеров системыпроисходит без деформаций, сооружение
называется
геометрически
изменяемой
системой (ГИС).
F
15.
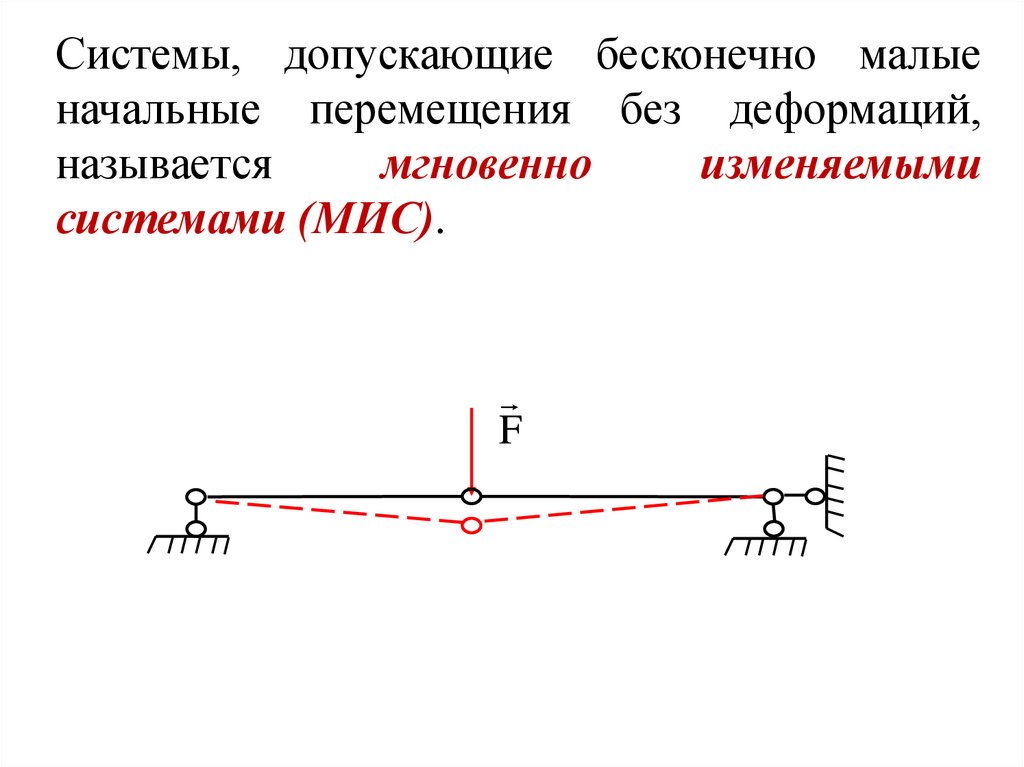
Системы, допускающие бесконечно малыеначальные перемещения без деформаций,
называется
мгновенно
изменяемыми
системами (МИС).
F
16.
• Кинематический анализ выполняют длявыявления ГИС и МИС. К проектированию
принимают
только
геометрически
неизменяемые системы.
• Различают количественный и качественный
анализ. Количественный – выполнение
необходимых, но недостаточных условий
ГНС. Качественный – анализ структуры
сооружения.
17.
Количественныйанализ
определяет
соотношение между числом степеней свободы
системы (числом уравнений статики, которые
мы можем записать для системы) nΔ и числом
связей, наложенных на систему nC:
W = nΔ – nC
18.
Статически определимой системой (СОС)называется геометрически неизменяемая
система, в которой все силовые факторы
( реакции внешних и внутренних связей,
включая внутренние усилия в сечениях
элементов ) могут быть найдены с помощью
одних лишь уравнений равновесия.
W = 0 - статически определимая система (СОС)
W<0 - статически неопределимая система (СНС)
19.
W>0геометрической изменяемая система (ГИС)
(механизм)
W = 0 или W<0
может быть геометрически неизменяемой или
мгновенно изменяемой системой (МИС)
20.
Для плоской системы:nD = 3D; nc = nвнут. св. + nвнеш. св. =
= 3П + 2H + C + C0
nвнут. cв.
nвнеш. cв.
D – количество дисков;
П – число простых припаек между дисками cистемы,
Н – число простых шарниров без учёта диска «земля»;
С – количество внутренних связей первого
типа ( линейных и угловых );
С0 – число внешних ( опорных ) связей – в
пересчёте на связи первого типа.
W = 3D – ( 3П + 2H + C + C0 )
21.
Простая припайка – жёсткое соединениедвух дисков.
Простой шарнир ( цилиндрический или
поступательный ) – шарнирное соединение
двух дисков.
Сложная ( кратная )
Сложный ( кратный )
припайка
шарнир
Соответствующее
( жёсткое или шарнирное )
соединение более чем двух
дисков
Учитываются эквивалентным числом
простых припаек ( шарниров ):
П = nD – 1 nD – число соединяемых дисков в узле H = nD – 1
22.
Для многопролётной балки:W = 3D –(2H+С0) ≤ 0.
D – количество дисков, Н – количество
простых
шаровых,
цилиндрических
шарниров, С0 – количество опорных
линейных и угловых связей.
23.
Качественный (структурный) анализ –это исследование структуры
расчётной схемы сооружения, заключающееся
в проверке правильности расположения
связей, выявлении возможных дефектов
соединения дисков и завершающееся
определением кинематического качества
(природы) системы (её геометрической
неизменяемости, изменяемости или
мгновенной изменяемости).
24.
Типовые способы соединения элементов,образующих диск
«Диада». Прикрепление точки А к диску с
помощью 2-х линейных связей. Оси связей не
должны располагаться на одной прямой.
25.
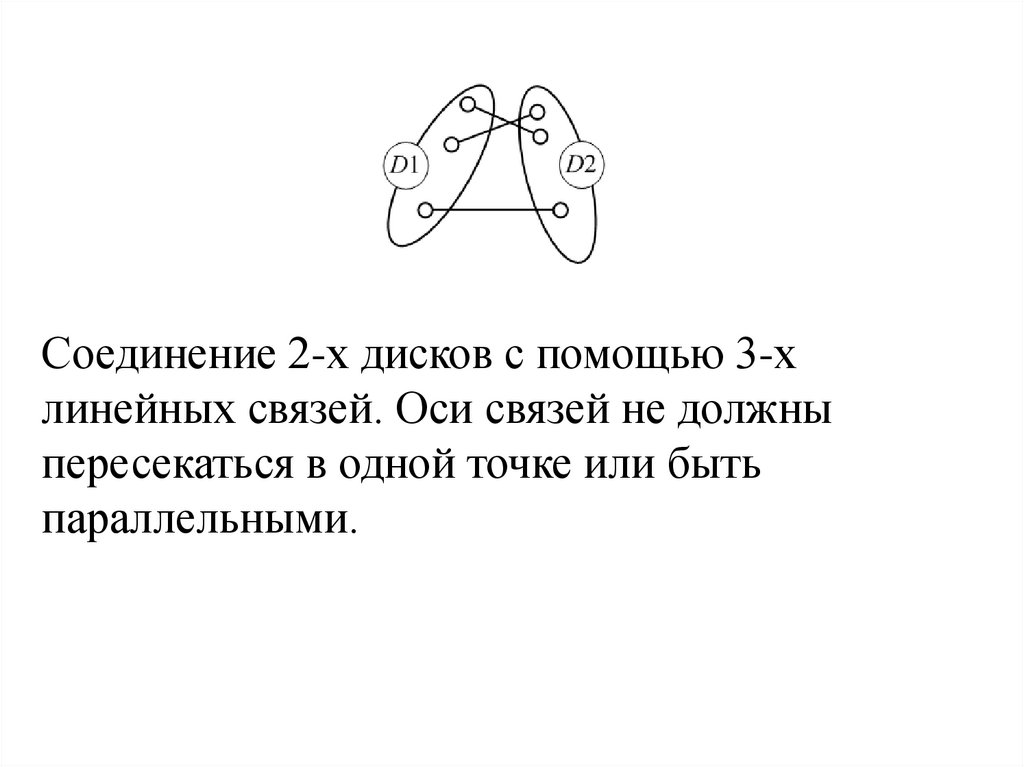
Соединение 2-х дисков с помощью 3-хлинейных связей. Оси связей не должны
пересекаться в одной точке или быть
параллельными.
26.
Соединение 2-х дисков с помощью шарнира А илинейной связи. Ось линейной связи не должна
проходить через центр шарнира А.
27.
Попарное соединение 3-х дисков с помощью3-х пар линейных связей. Мгновенные центры
вращения 3-х дисков (12, 13, 23) не должны
лежать на одной прямой.
28.
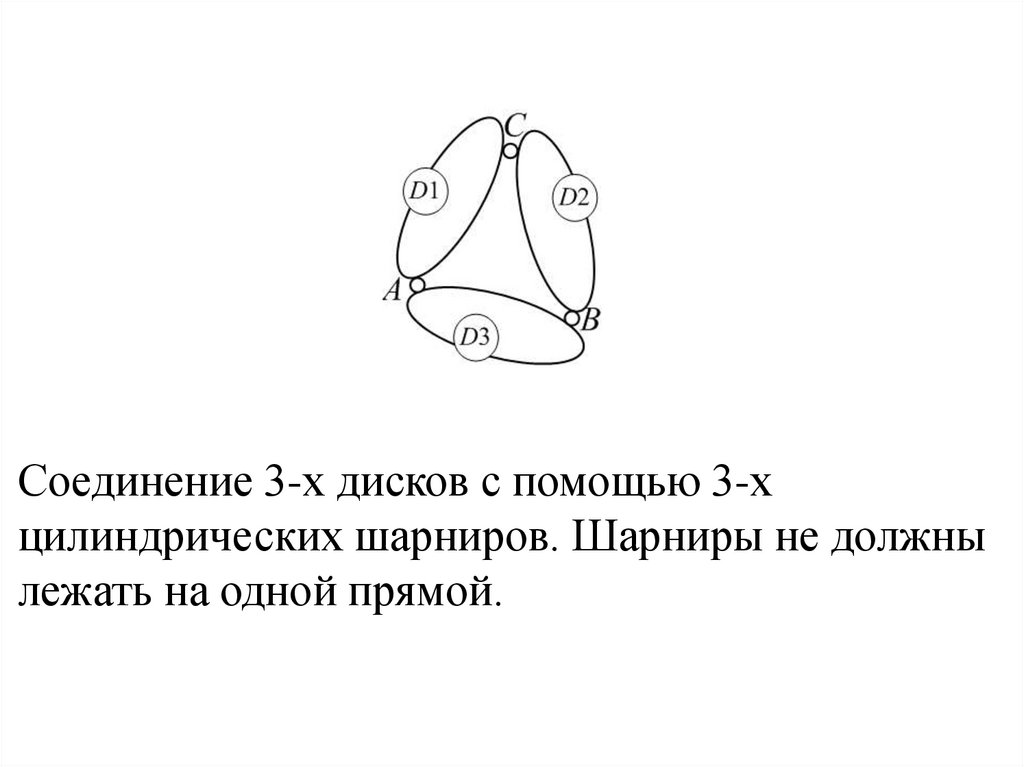
Соединение 3-х дисков с помощью 3-хцилиндрических шарниров. Шарниры не должны
лежать на одной прямой.
29.
Главной называется геометрически неизменяемая частьсоставной системы, способная воспринимать любые
воздействия даже при отсутствии всех других частей.
Второстепенная часть составной системы – это часть,
утрачивающая
работоспособность
вследствие
возникновения её геометрической или мгновенной
изменяемости при удалении других частей (всех или
некоторых).
30.
Кинематический анализ многопролётной балкиКоличественный анализ:
W = 3D –(2H+С0); W = 3∙4–(2 ∙3 +6)=0
Вывод:
1) система является статически определимой
системой (СОС);
2) Выполняется необходимое, но не достаточное
условие того, что система является
геометрически неизменяемой системой (ГНС).
31.
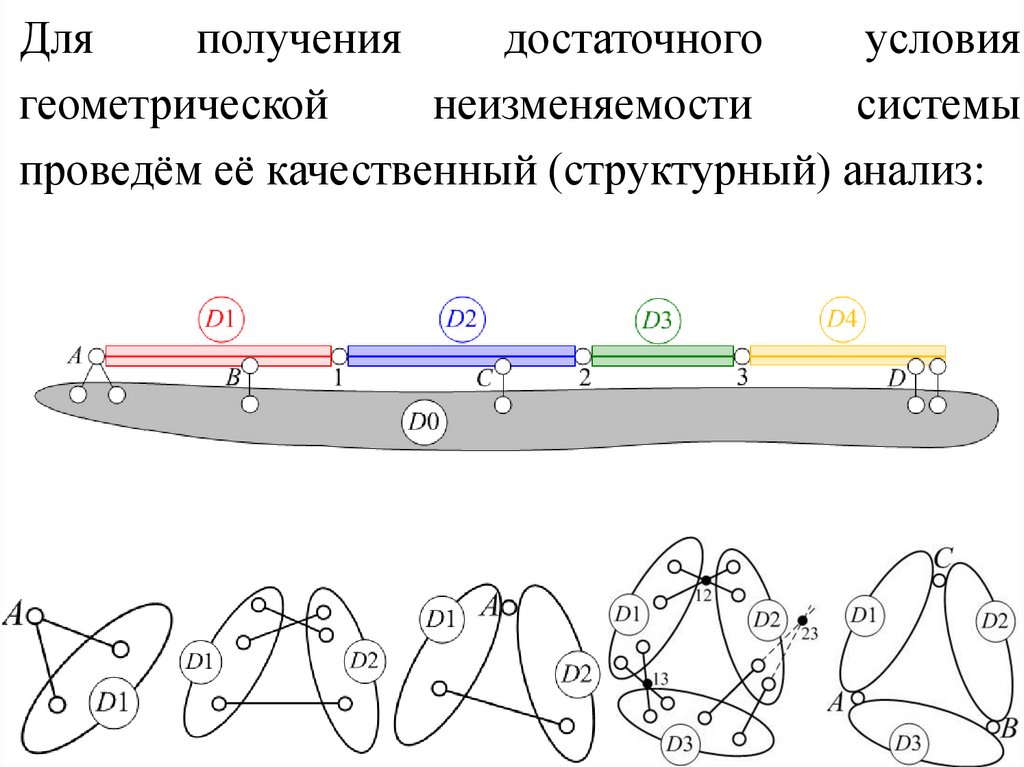
Дляполучения
достаточного
условия
геометрической
неизменяемости
системы
проведём её качественный (структурный) анализ:
32.
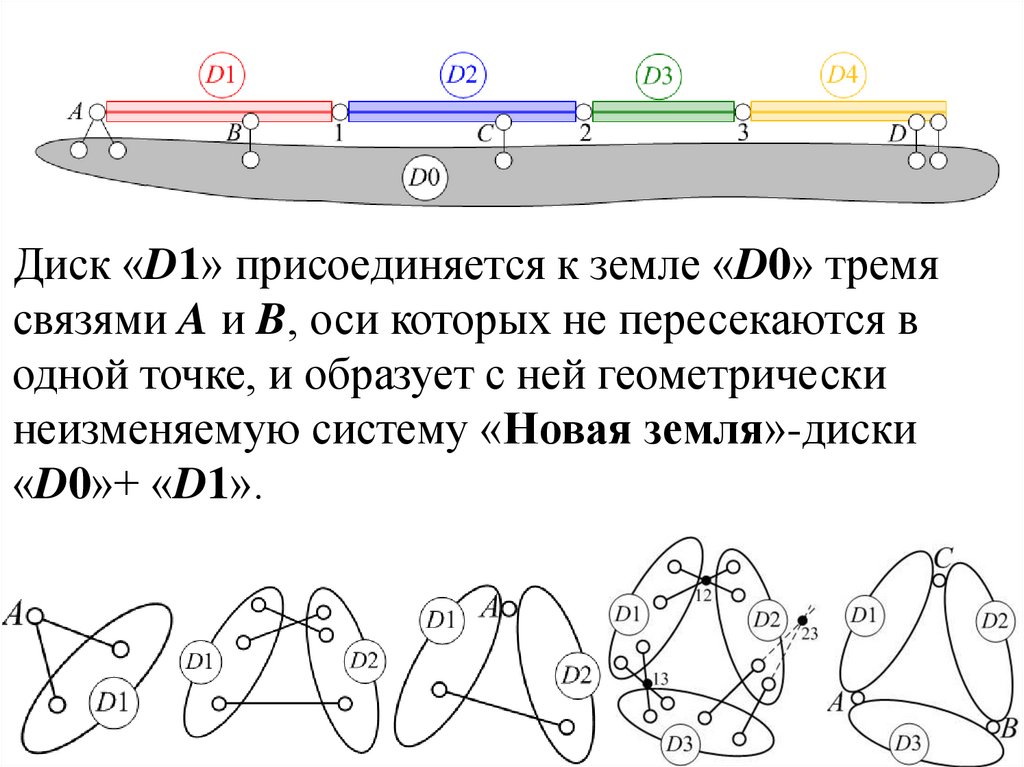
Диск «D1» присоединяется к земле «D0» тремясвязями A и B, оси которых не пересекаются в
одной точке, и образует с ней геометрически
неизменяемую систему «Новая земля»-диски
«D0»+ «D1».
33.
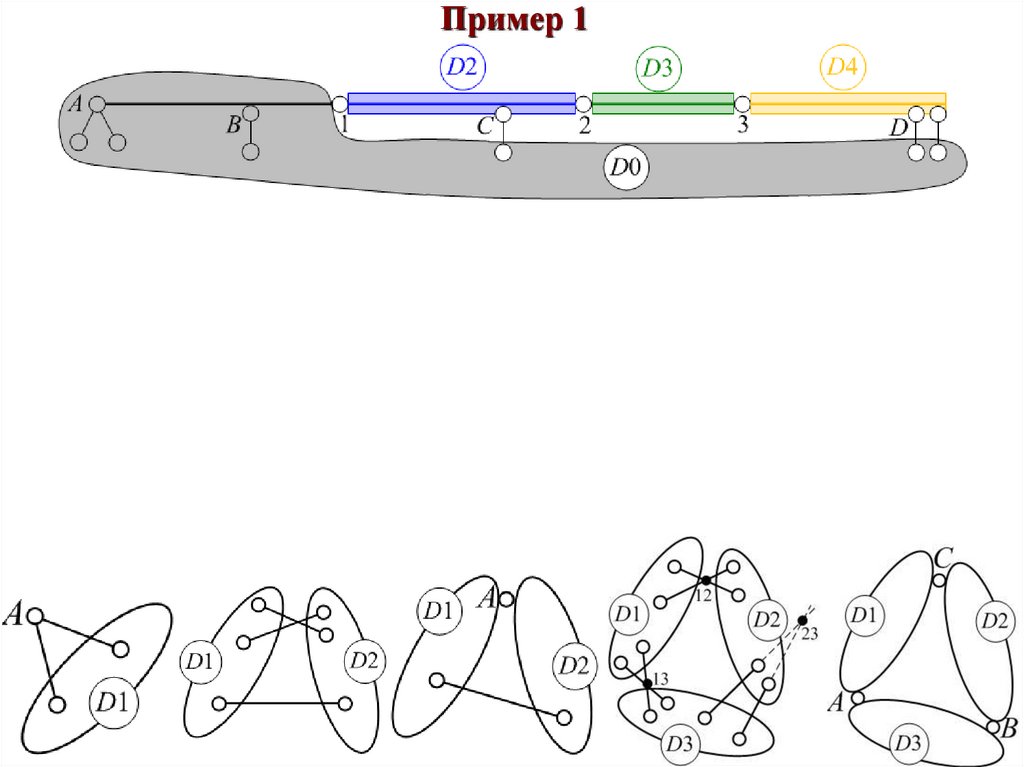
Пример 134.
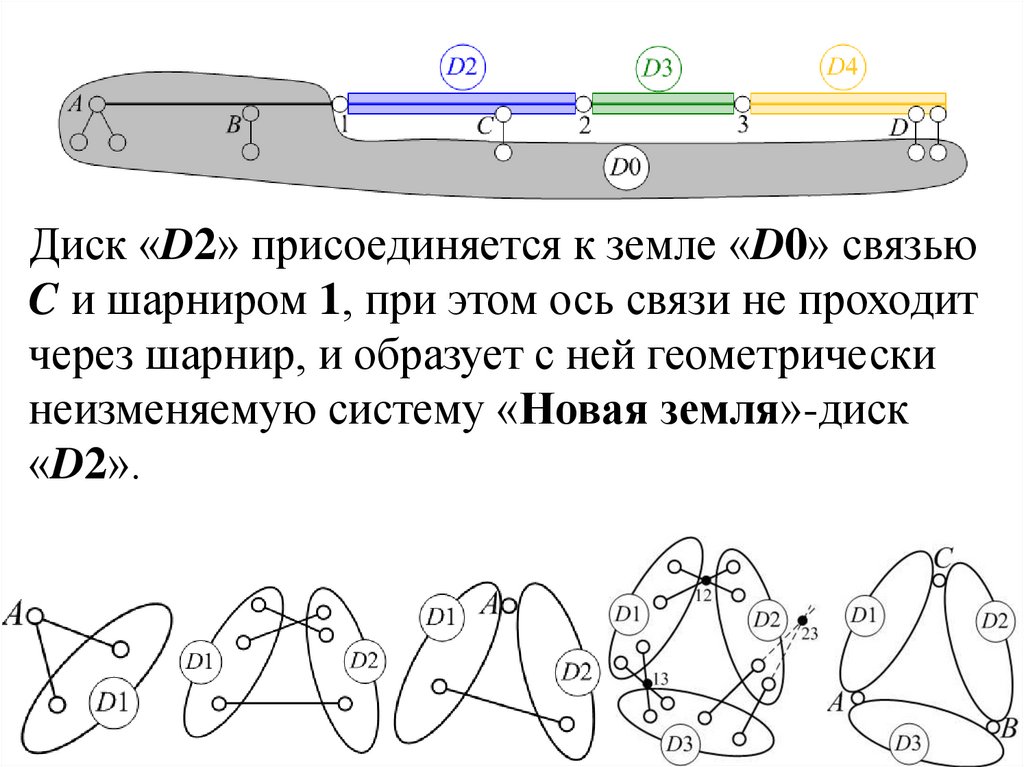
Диск «D2» присоединяется к земле «D0» связьюC и шарниром 1, при этом ось связи не проходит
через шарнир, и образует с ней геометрически
неизменяемую систему «Новая земля»-диск
«D2».
35.
36.
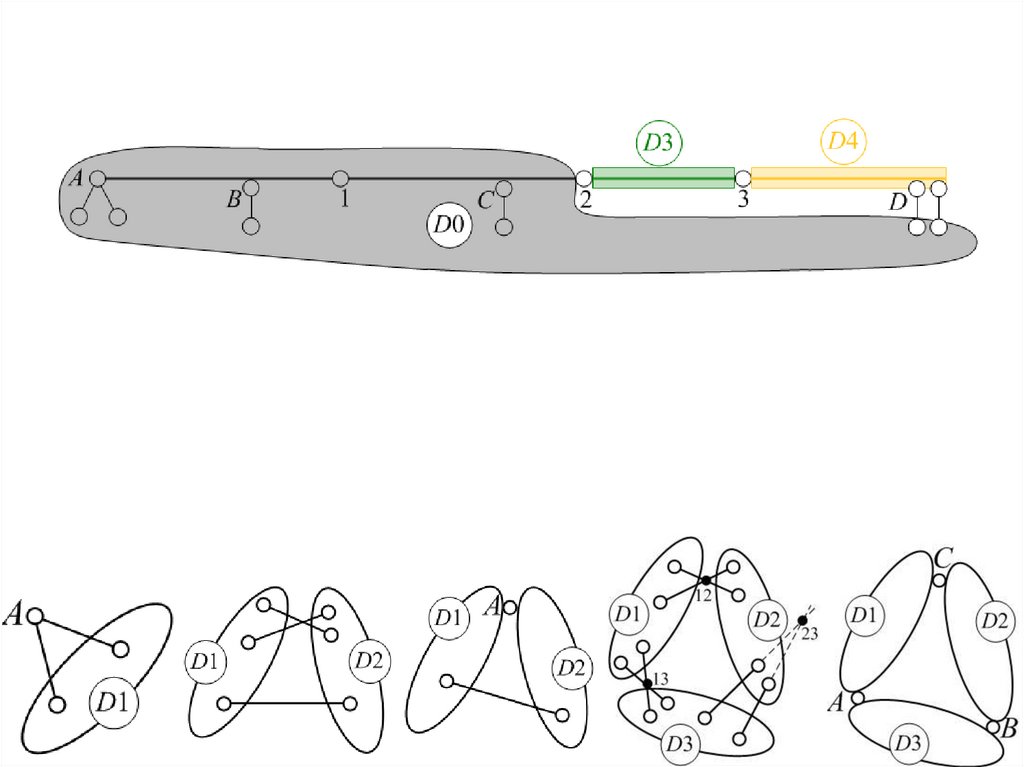
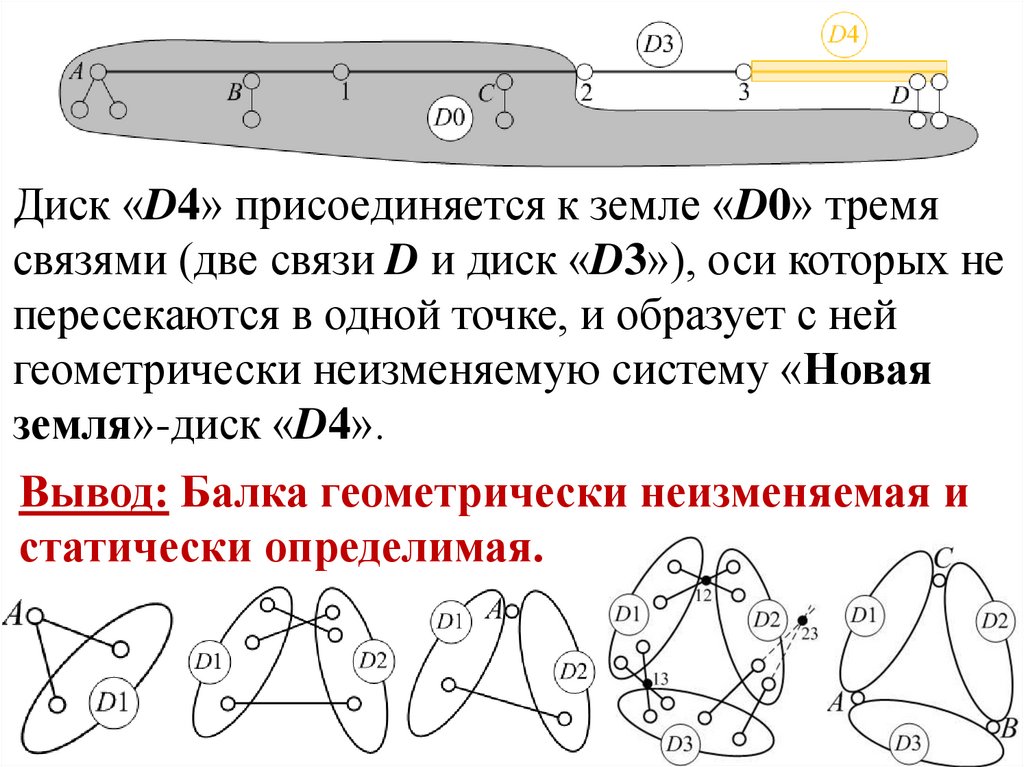
Диск «D4» присоединяется к земле «D0» тремясвязями (две связи D и диск «D3»), оси которых не
пересекаются в одной точке, и образует с ней
геометрически неизменяемую систему «Новая
земля»-диск «D4».
Вывод: Балка геометрически неизменяемая и
статически определимая.
37.
Кинематический анализ фермыКоличественный анализ:
W = 2У –(С+С0 )
W = 2∙10–(17 +3)=0
Отсюда следует, что:
1) система является статически определимой
системой (СОС);
2) Выполняется необходимое, но не достаточное
условие того, что система является
геометрически неизменяемой системой (ГНС).
38.
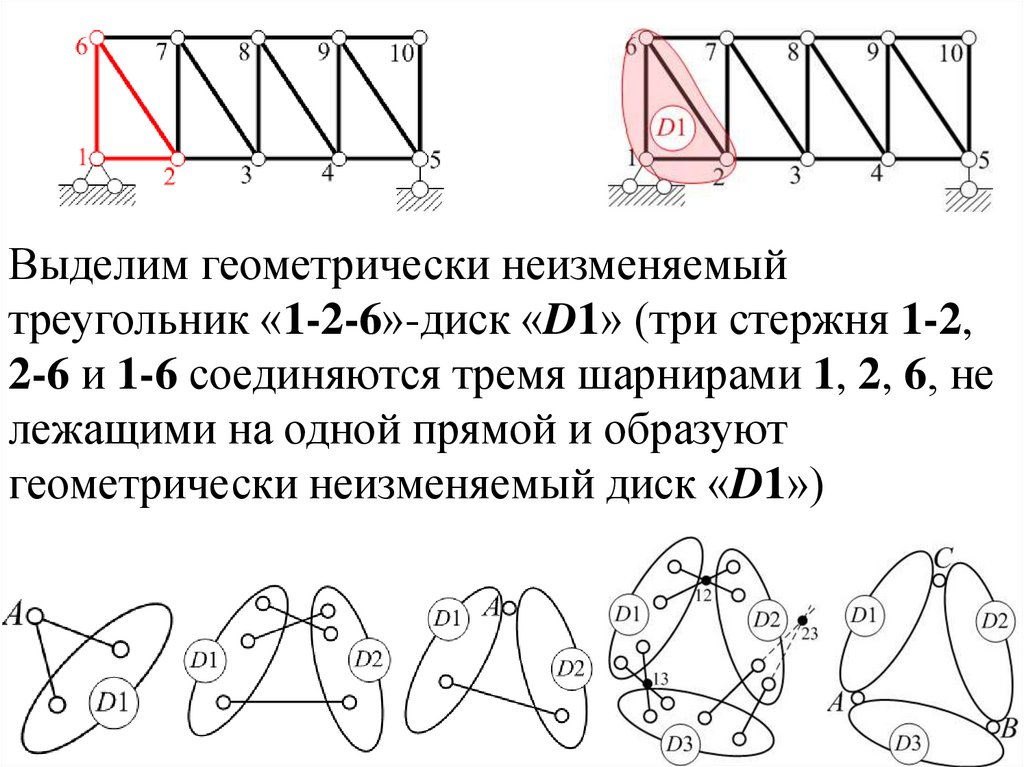
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»)
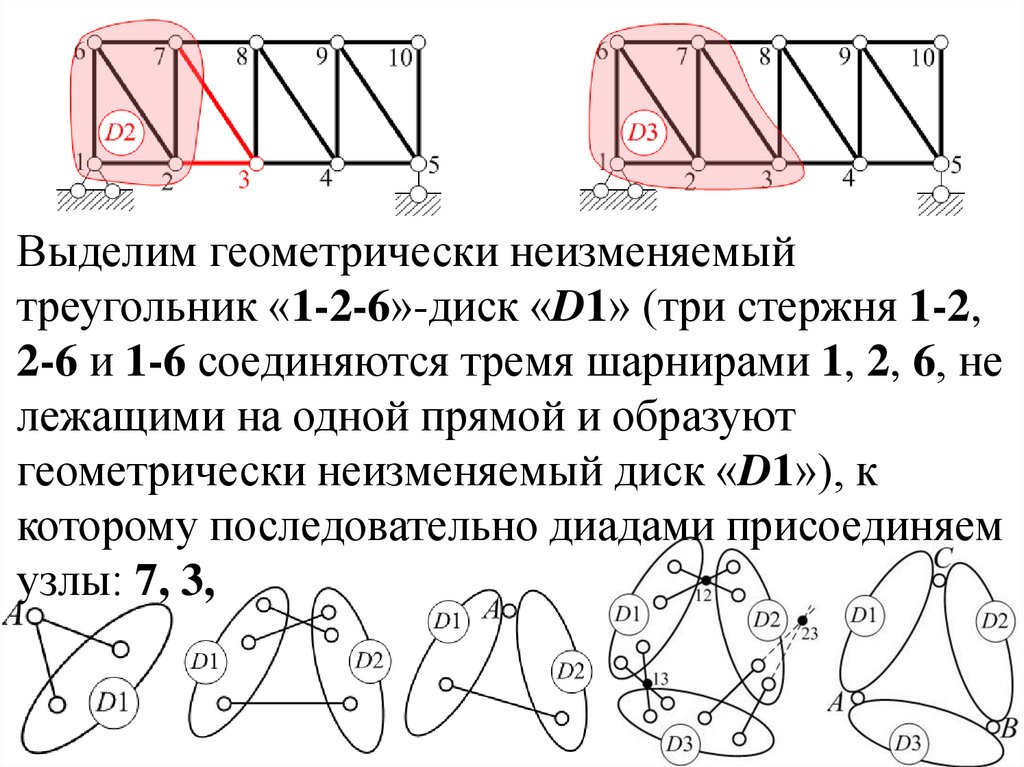
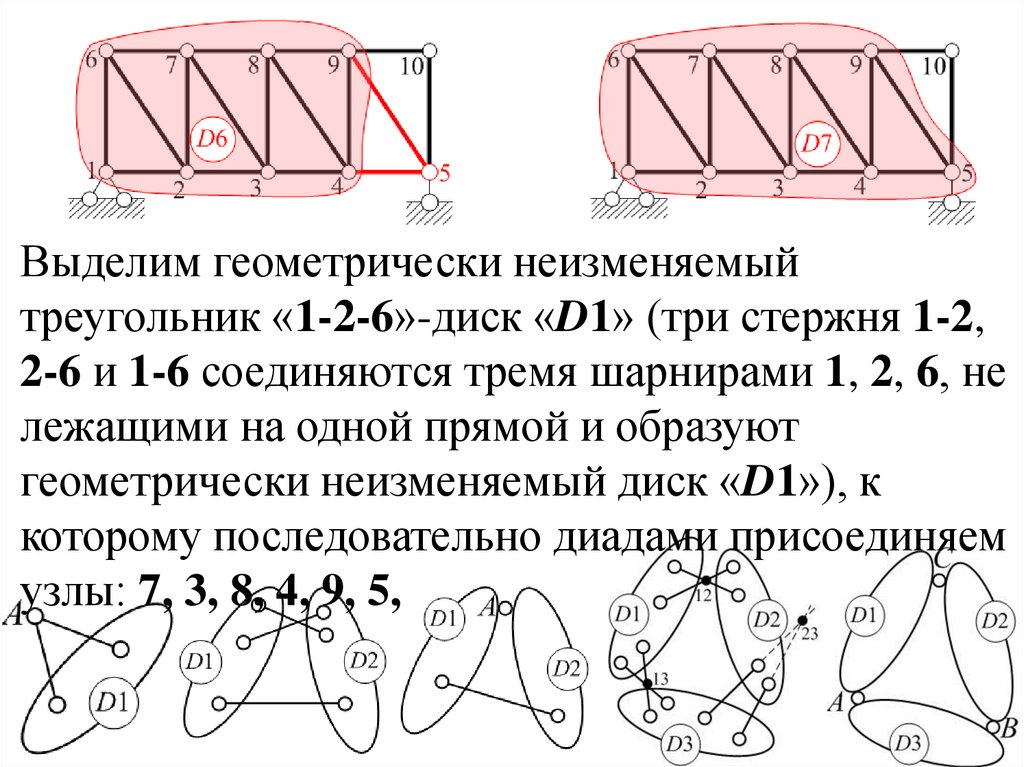
39.
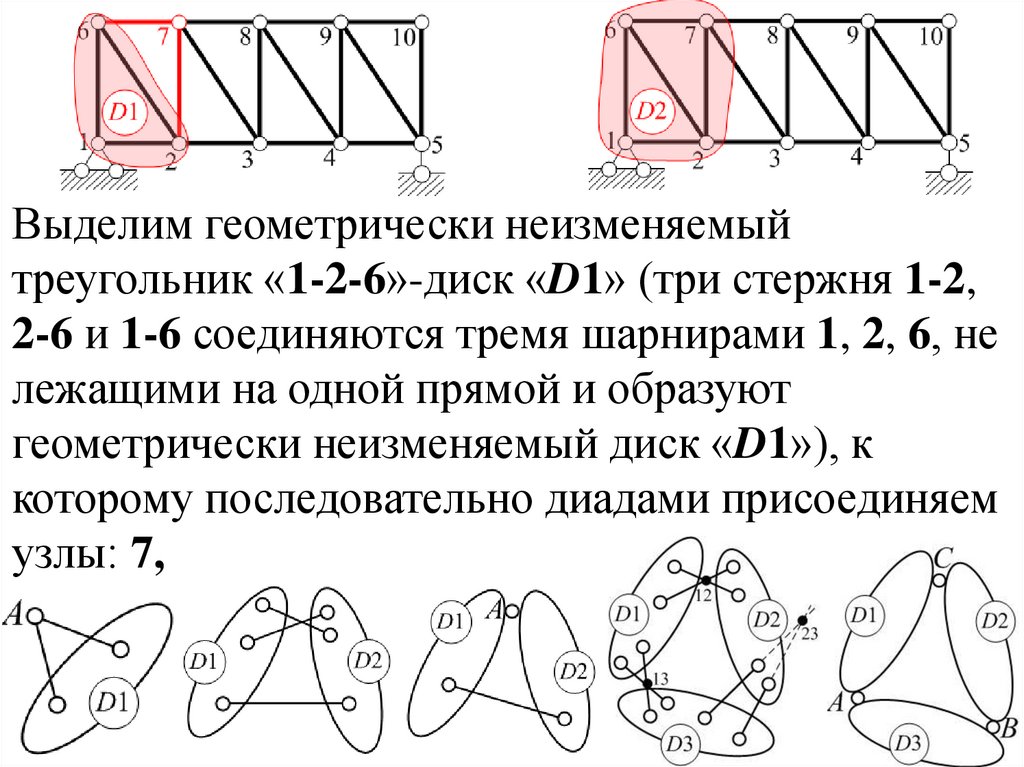
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7,
40.
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7, 3,
41.
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7, 3, 8,
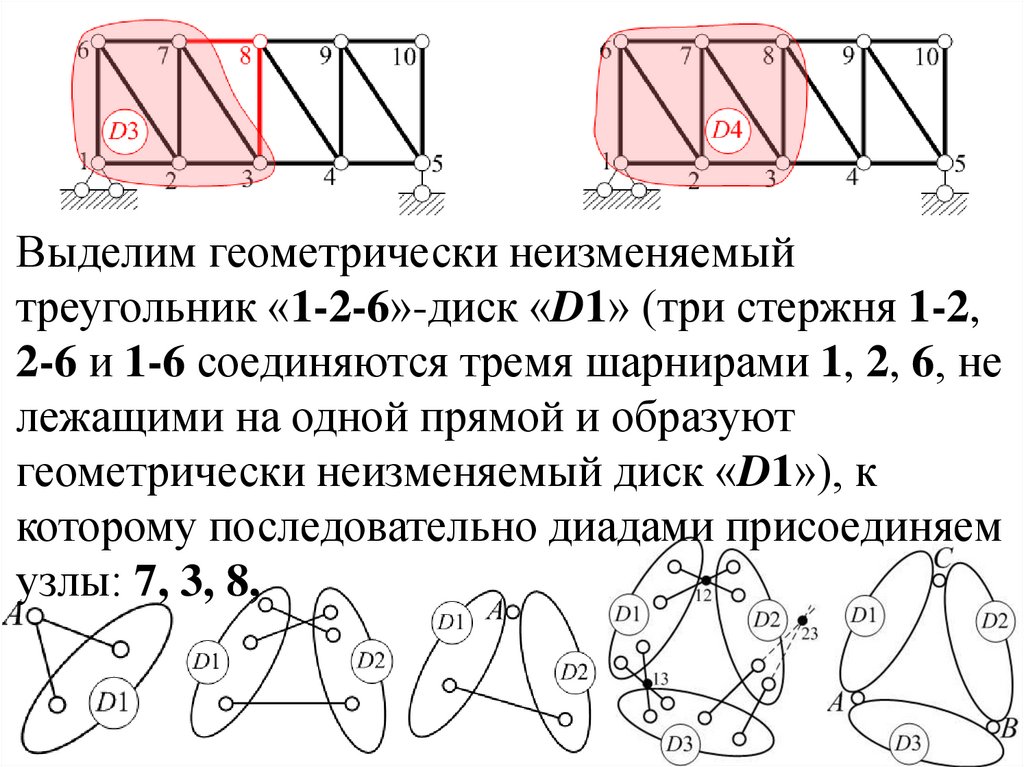
42.
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7, 3, 8, 4,
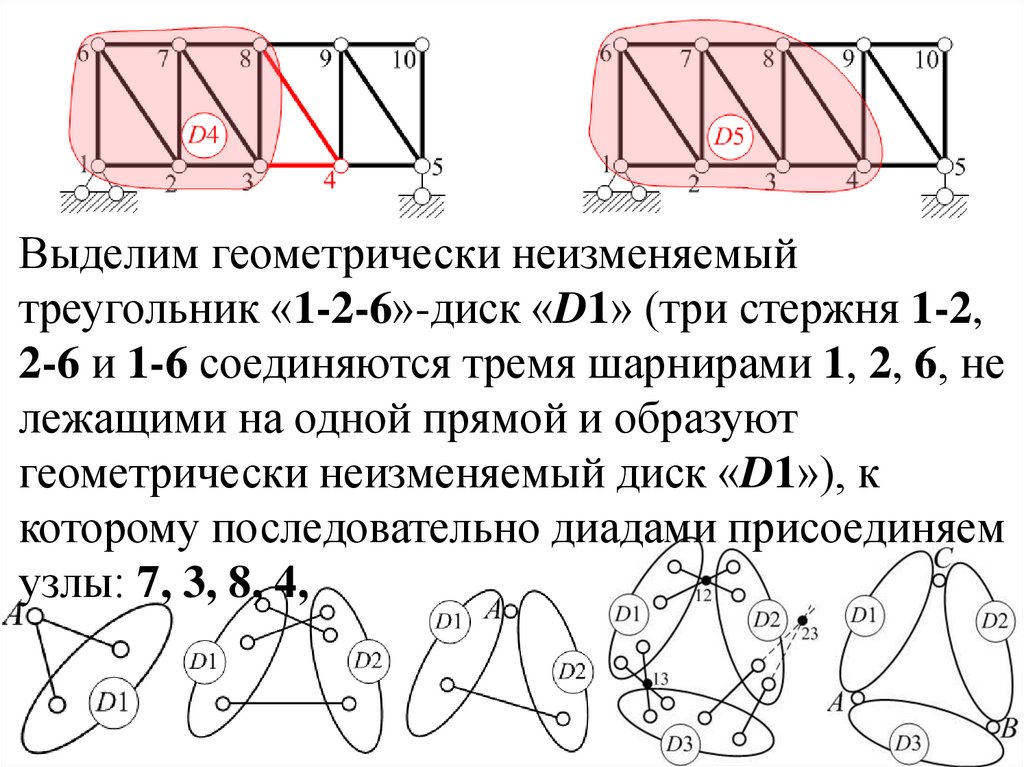
43.
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7, 3, 8, 4, 9,
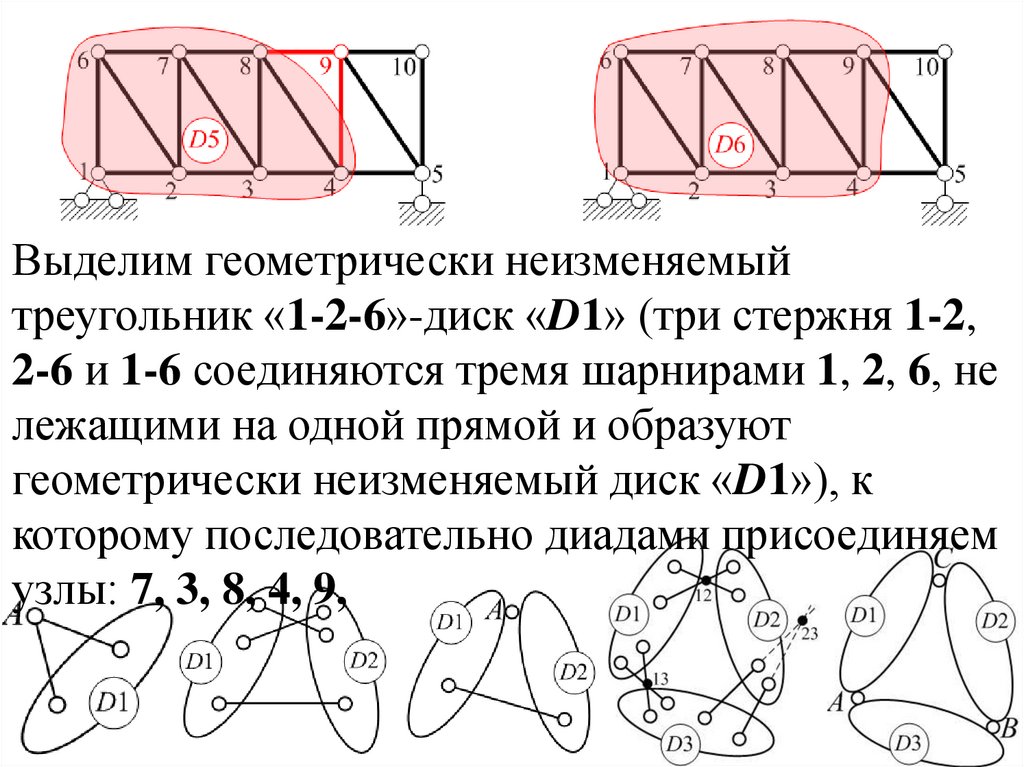
44.
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7, 3, 8, 4, 9, 5,
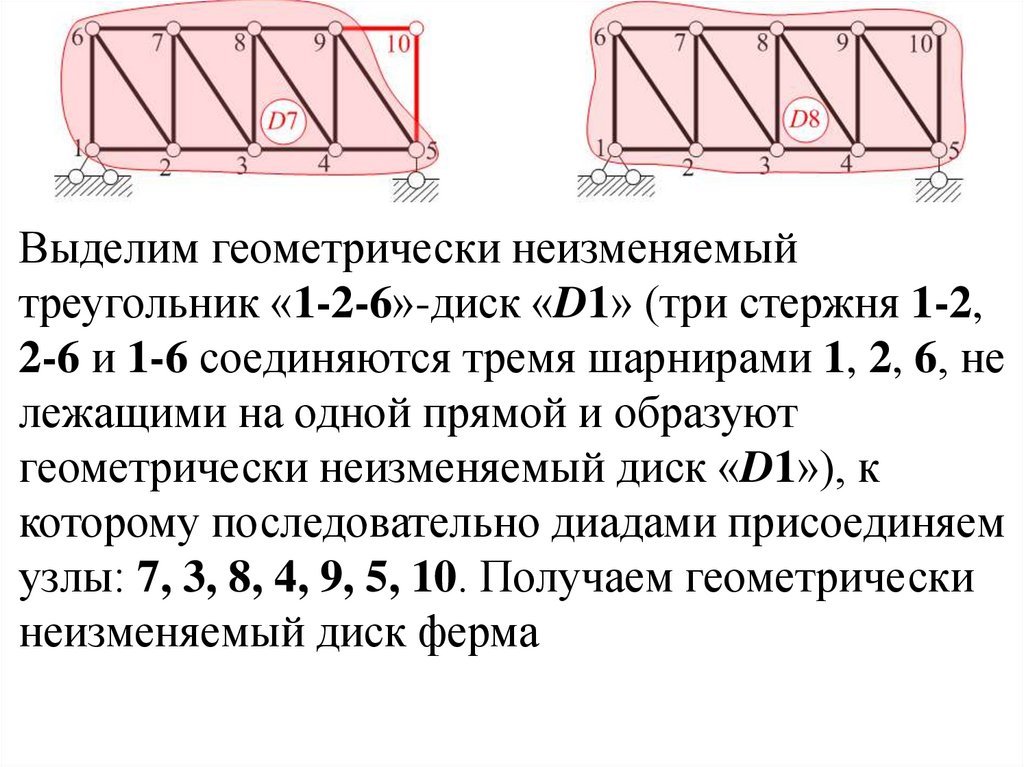
45.
Выделим геометрически неизменяемыйтреугольник «1-2-6»-диск «D1» (три стержня 1-2,
2-6 и 1-6 соединяются тремя шарнирами 1, 2, 6, не
лежащими на одной прямой и образуют
геометрически неизменяемый диск «D1»), к
которому последовательно диадами присоединяем
узлы: 7, 3, 8, 4, 9, 5, 10. Получаем геометрически
неизменяемый диск ферма
46.
Получаем геометрически неизменяемый диск«D8», который к земле «D0» крепится при помощи
трех связей в узлах 1 и 5, оси которых не
пересекаются в одной точке.
Вывод: Ферма геометрически неизменяемая и
статически определимая.
47.
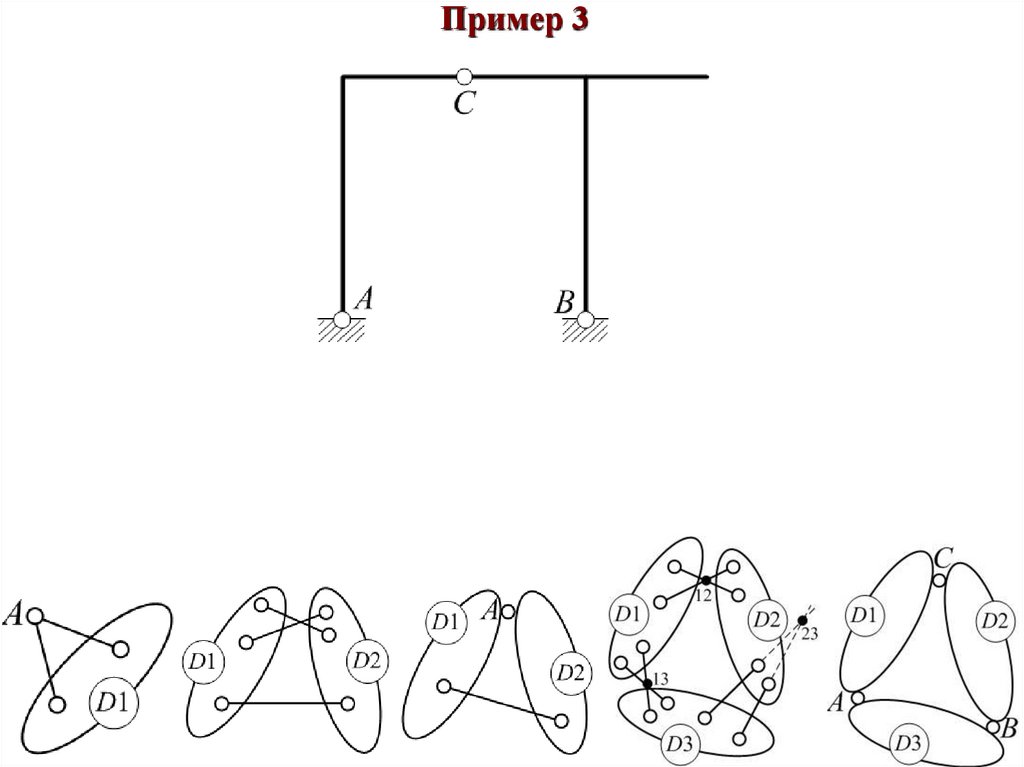
Пример 348.
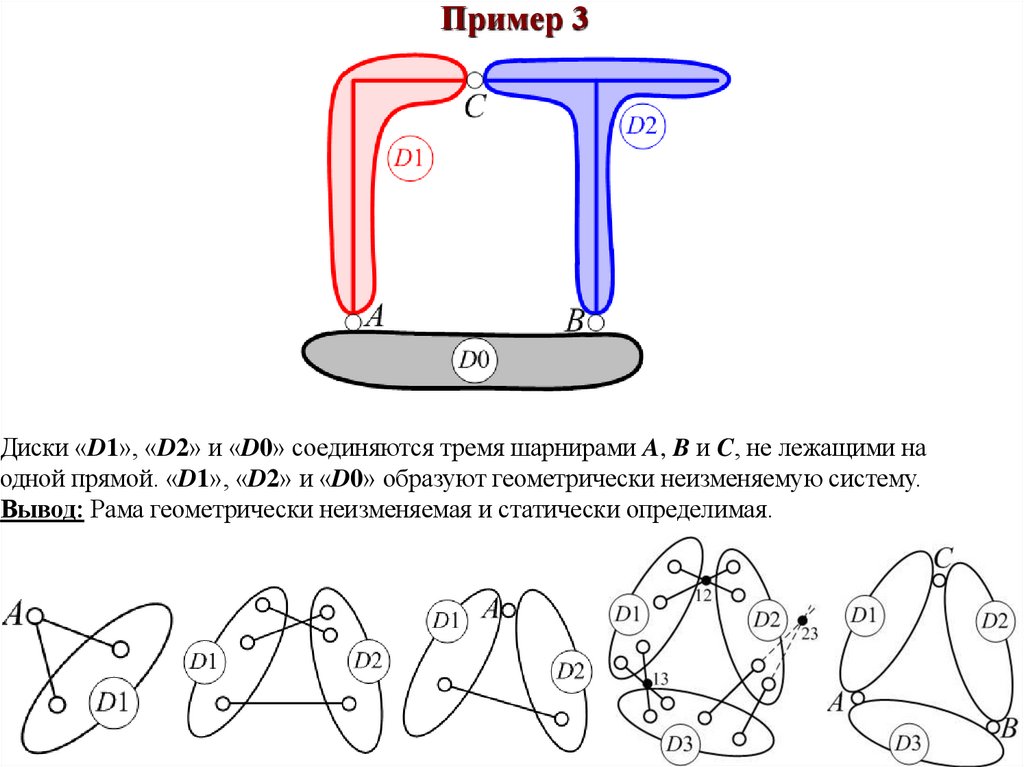
Пример 3Диски «D1», «D2» и «D0» соединяются тремя шарнирами A, B и C, не лежащими на
одной прямой. «D1», «D2» и «D0» образуют геометрически неизменяемую систему.
Вывод: Рама геометрически неизменяемая и статически определимая.
49.
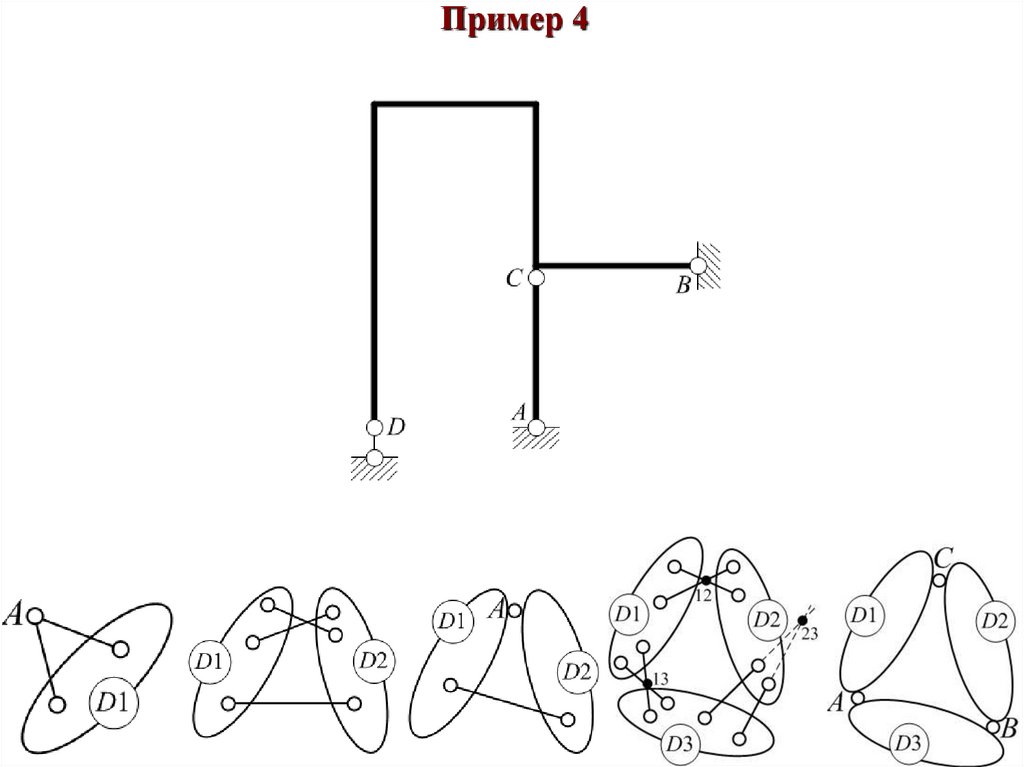
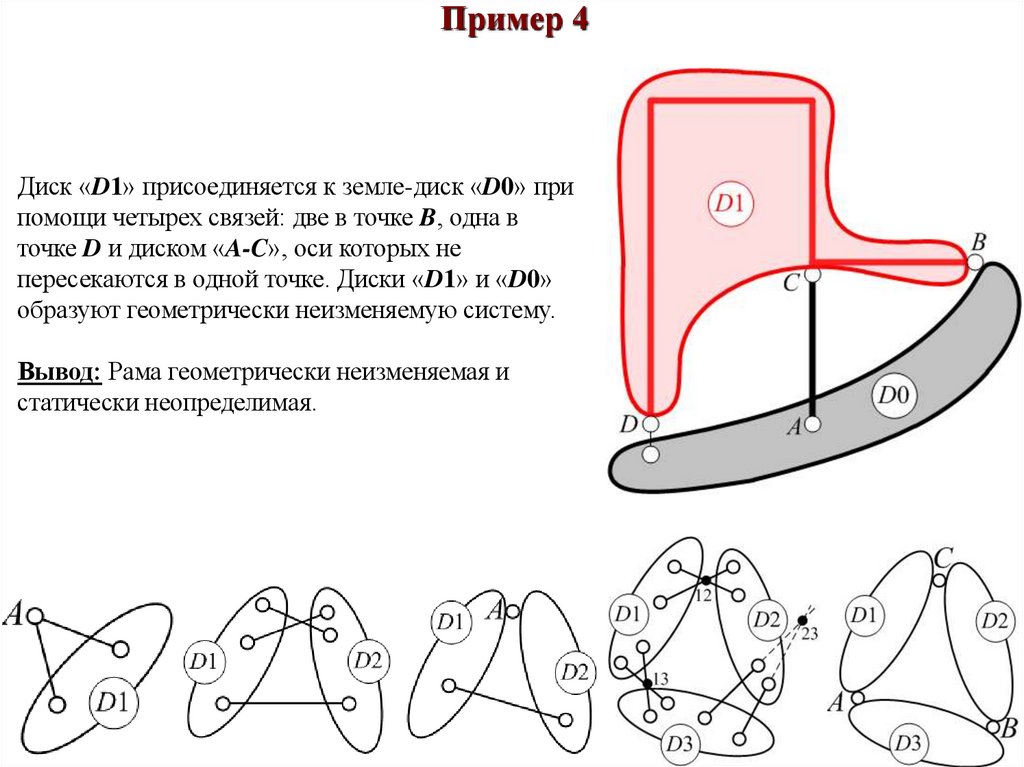
Пример 450.
Пример 4Диск «D1» присоединяется к земле-диск «D0» при
помощи четырех связей: две в точке B, одна в
точке D и диском «A-C», оси которых не
пересекаются в одной точке. Диски «D1» и «D0»
образуют геометрически неизменяемую систему.
Вывод: Рама геометрически неизменяемая и
статически неопределимая.
51.
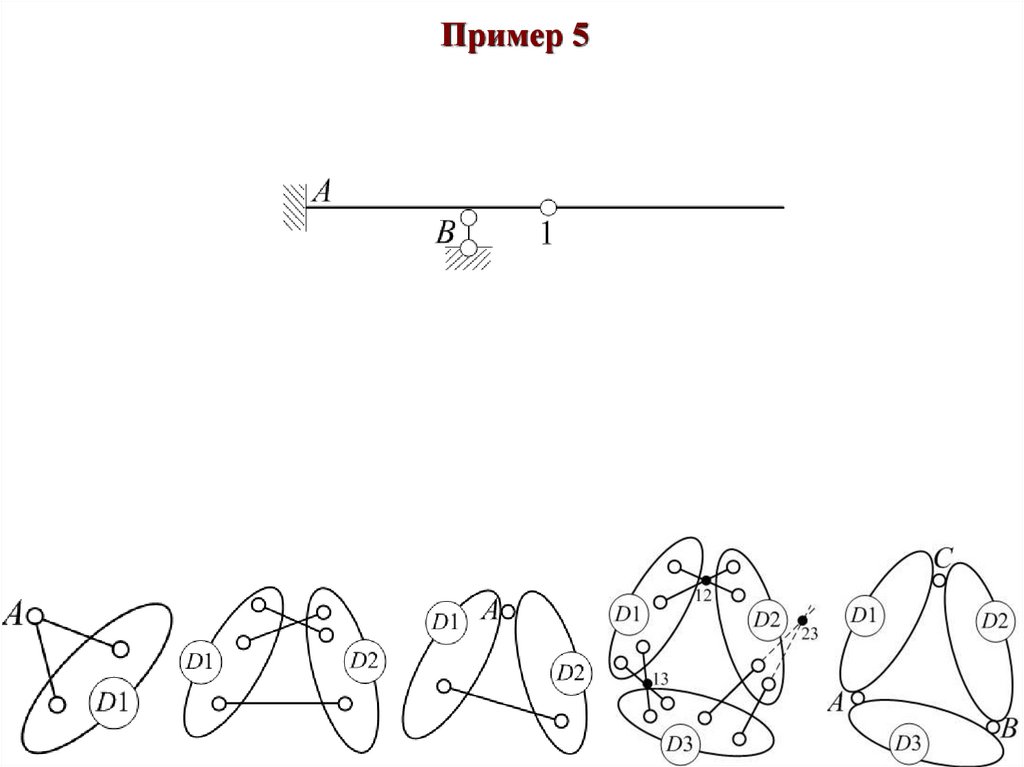
Пример 552.
Пример 553.
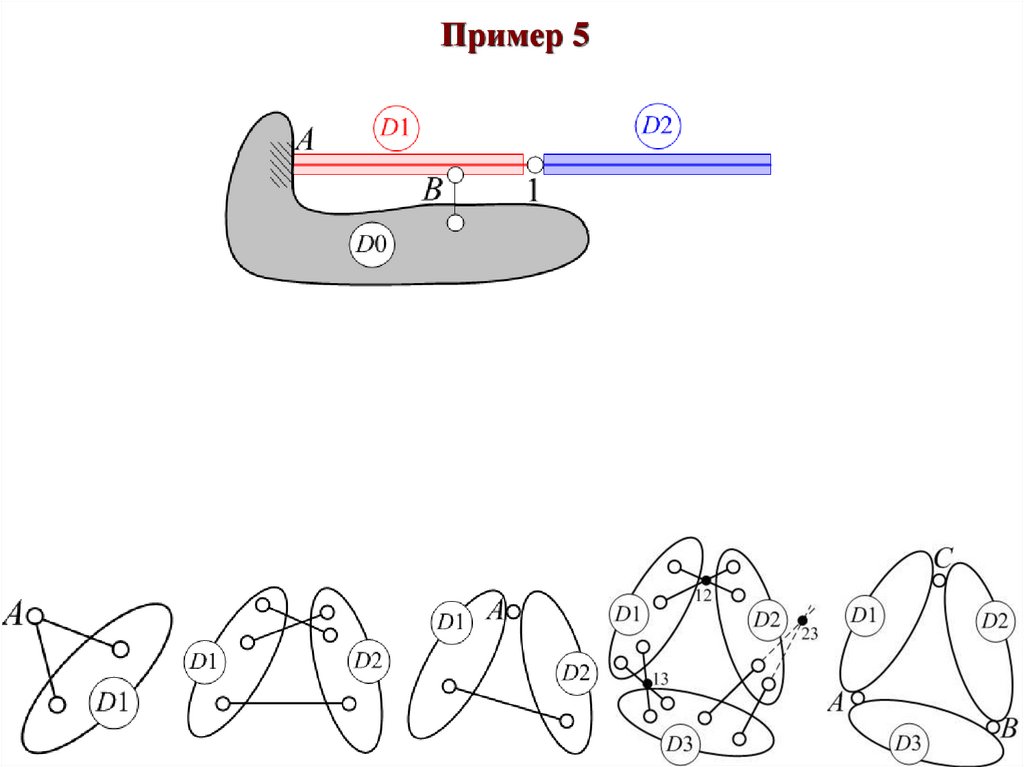
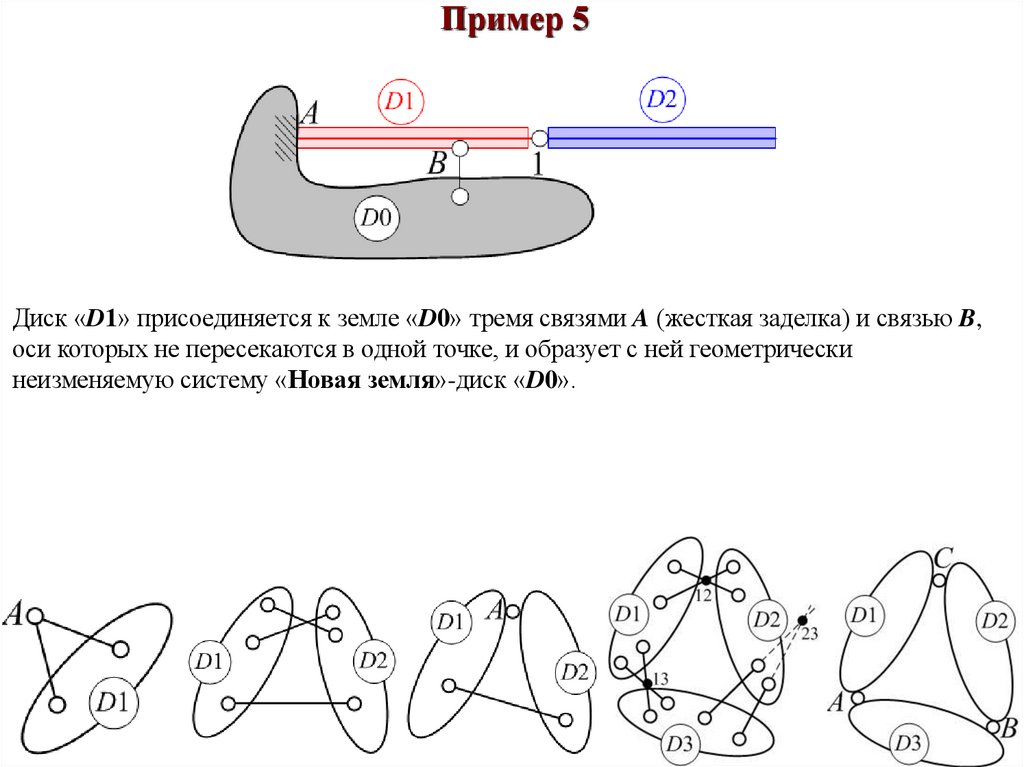
Пример 5Диск «D1» присоединяется к земле «D0» тремя связями A (жесткая заделка) и связью B,
оси которых не пересекаются в одной точке, и образует с ней геометрически
неизменяемую систему «Новая земля»-диск «D0».
54.
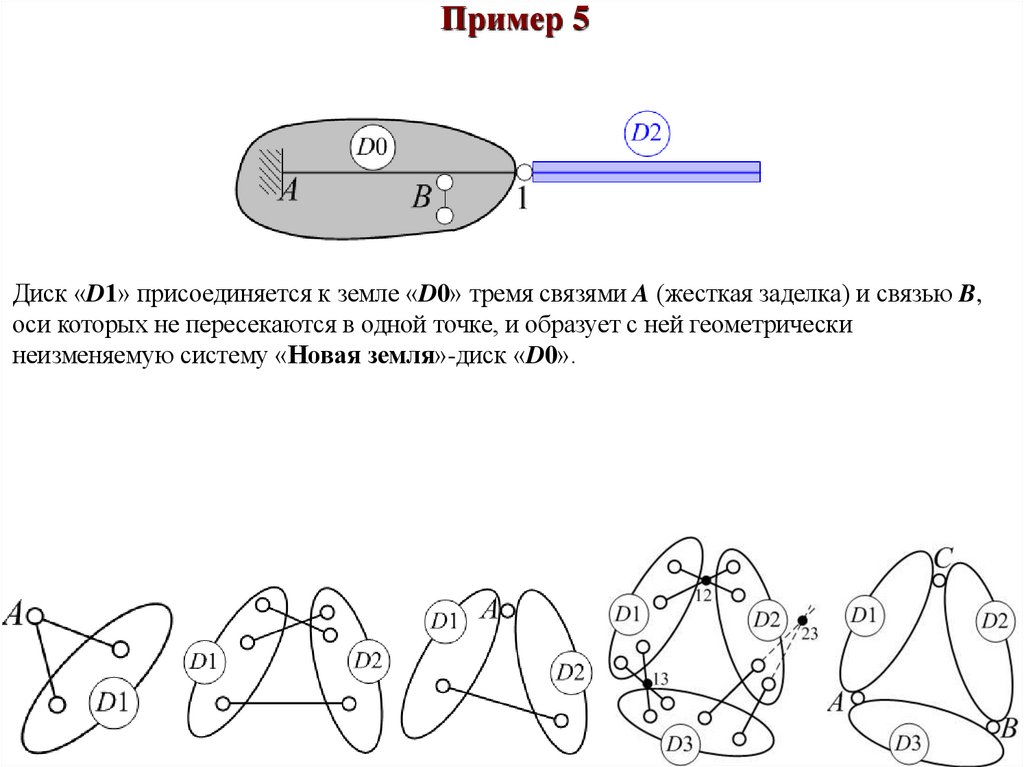
Пример 5Диск «D1» присоединяется к земле «D0» тремя связями A (жесткая заделка) и связью B,
оси которых не пересекаются в одной точке, и образует с ней геометрически
неизменяемую систему «Новая земля»-диск «D0».
55.
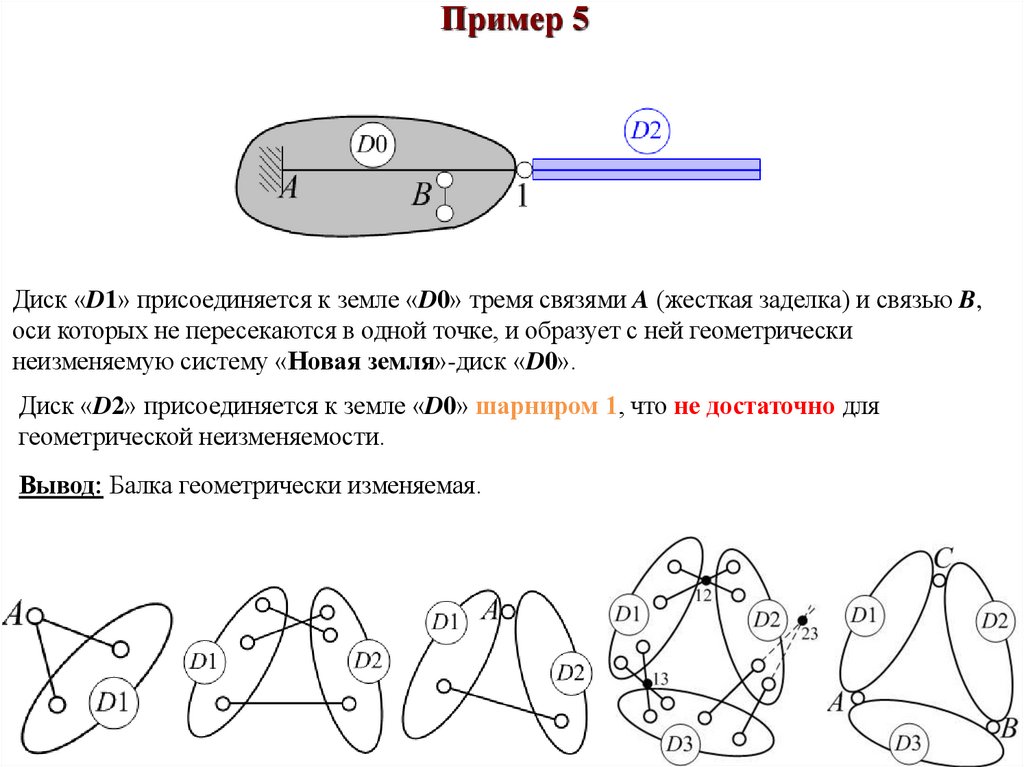
Пример 5Диск «D1» присоединяется к земле «D0» тремя связями A (жесткая заделка) и связью B,
оси которых не пересекаются в одной точке, и образует с ней геометрически
неизменяемую систему «Новая земля»-диск «D0».
Диск «D2» присоединяется к земле «D0» шарниром 1, что не достаточно для
геометрической неизменяемости.
Вывод: Балка геометрически изменяемая.
56.
Пример 657.
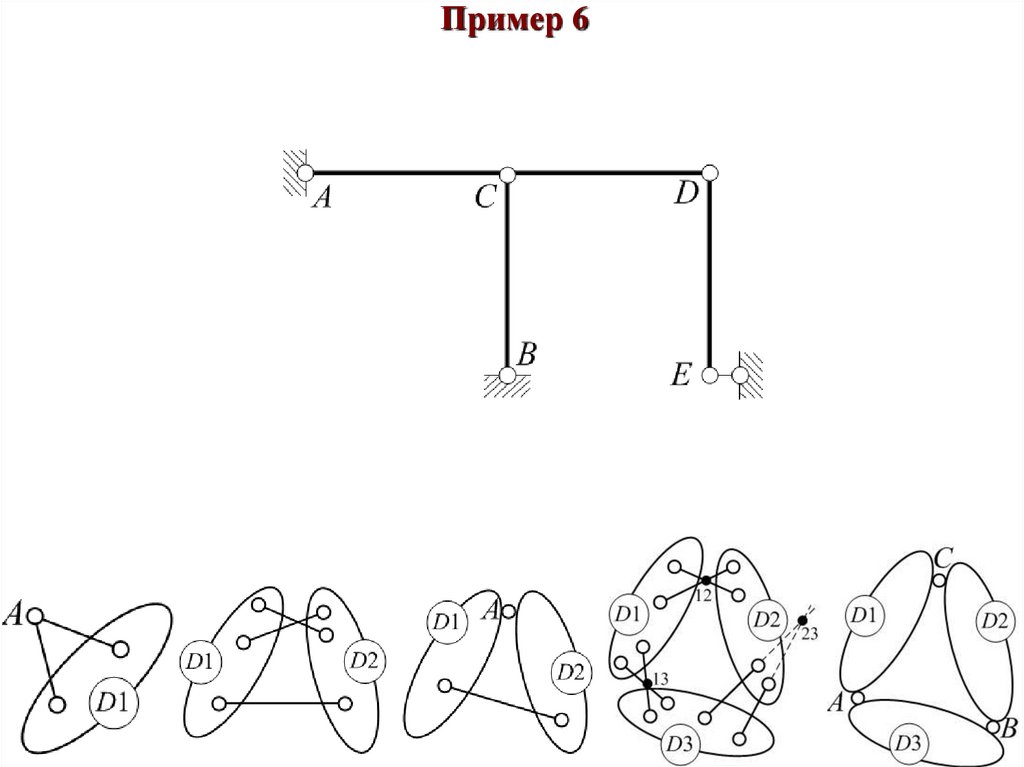
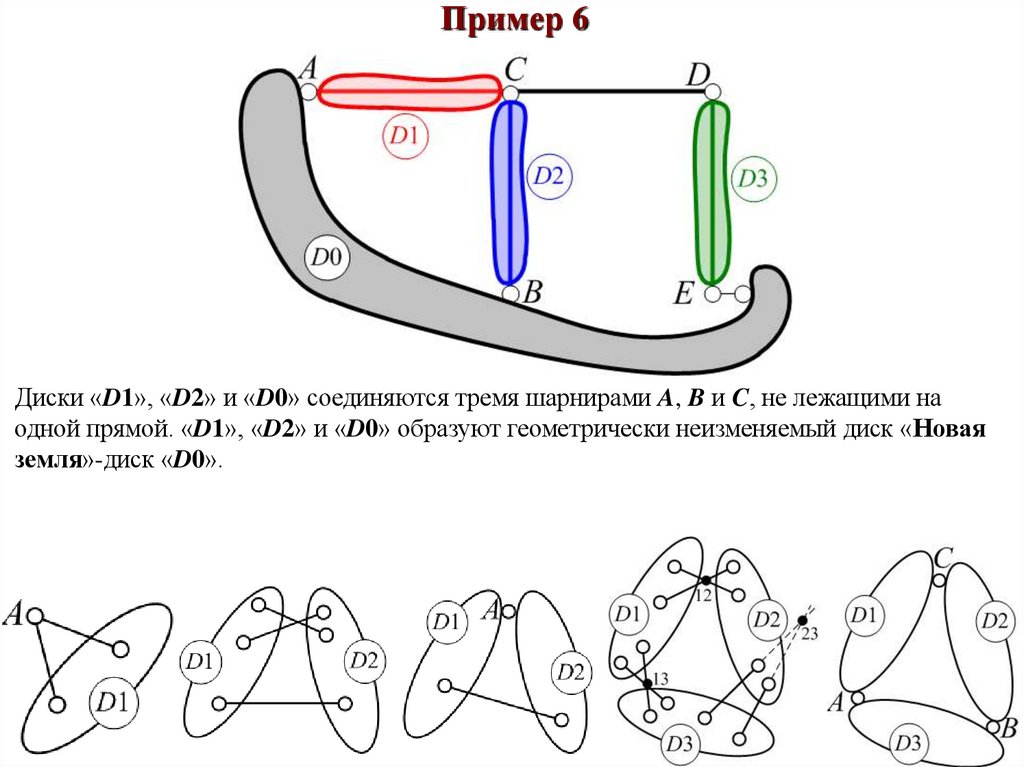
Пример 6Диски «D1», «D2» и «D0» соединяются тремя шарнирами A, B и C, не лежащими на
одной прямой. «D1», «D2» и «D0» образуют геометрически неизменяемый диск «Новая
земля»-диск «D0».
58.
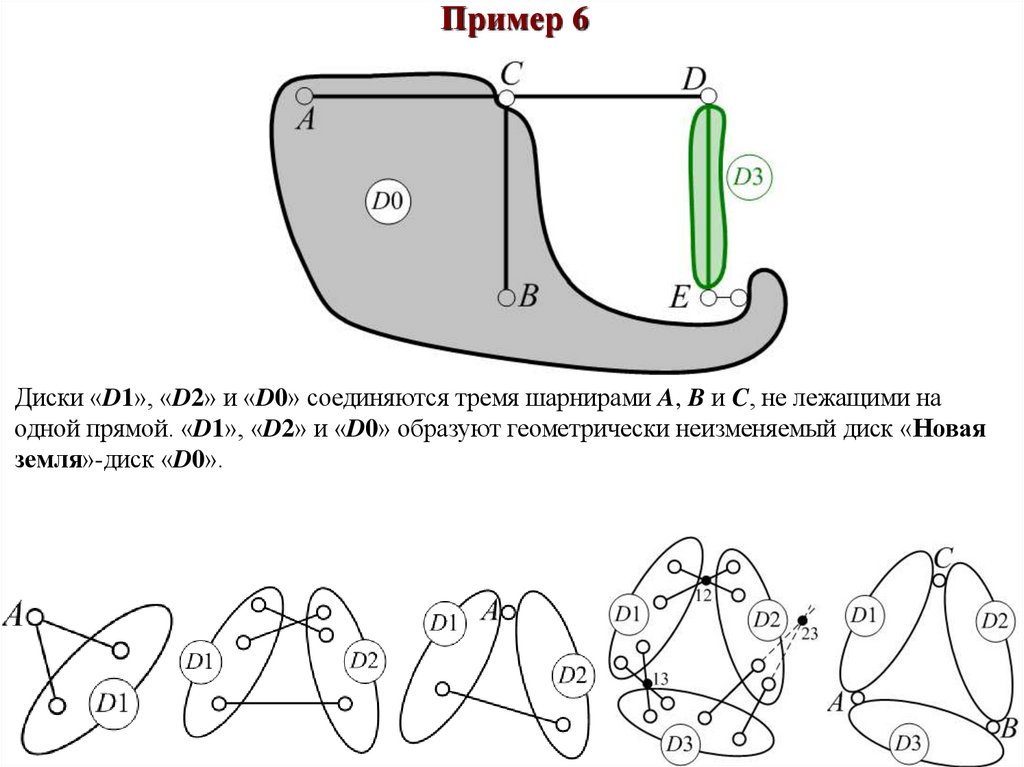
Пример 6Диски «D1», «D2» и «D0» соединяются тремя шарнирами A, B и C, не лежащими на
одной прямой. «D1», «D2» и «D0» образуют геометрически неизменяемый диск «Новая
земля»-диск «D0».
59.
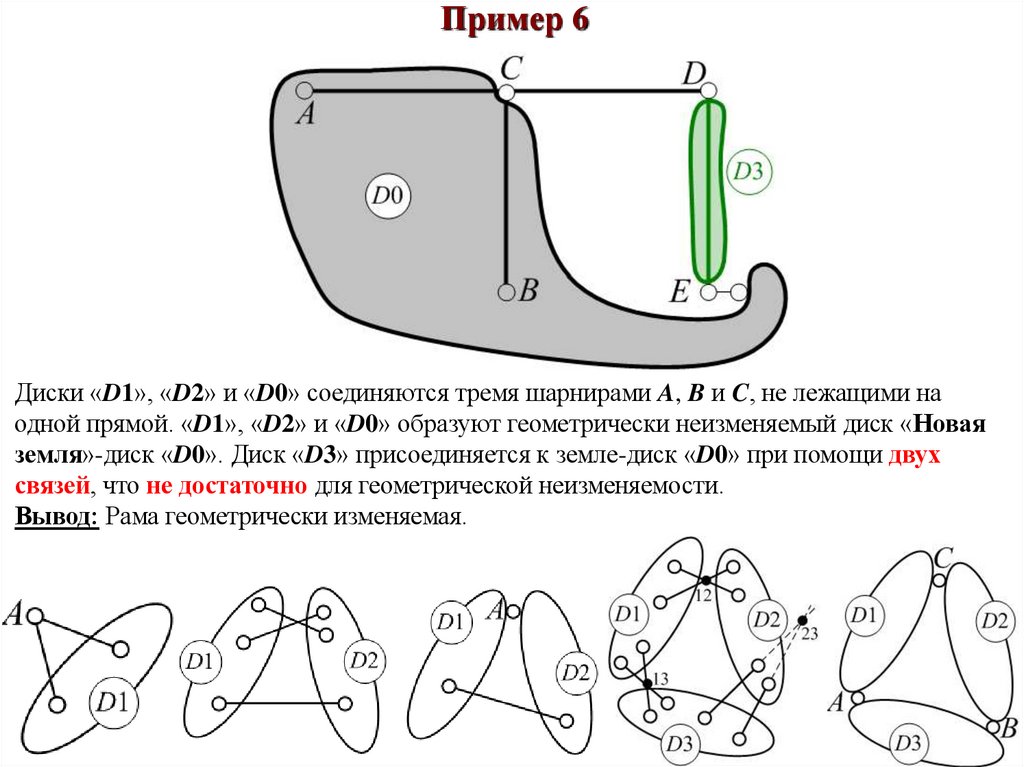
Пример 6Диски «D1», «D2» и «D0» соединяются тремя шарнирами A, B и C, не лежащими на
одной прямой. «D1», «D2» и «D0» образуют геометрически неизменяемый диск «Новая
земля»-диск «D0». Диск «D3» присоединяется к земле-диск «D0» при помощи двух
связей, что не достаточно для геометрической неизменяемости.
Вывод: Рама геометрически изменяемая.
60.
Пример 761.
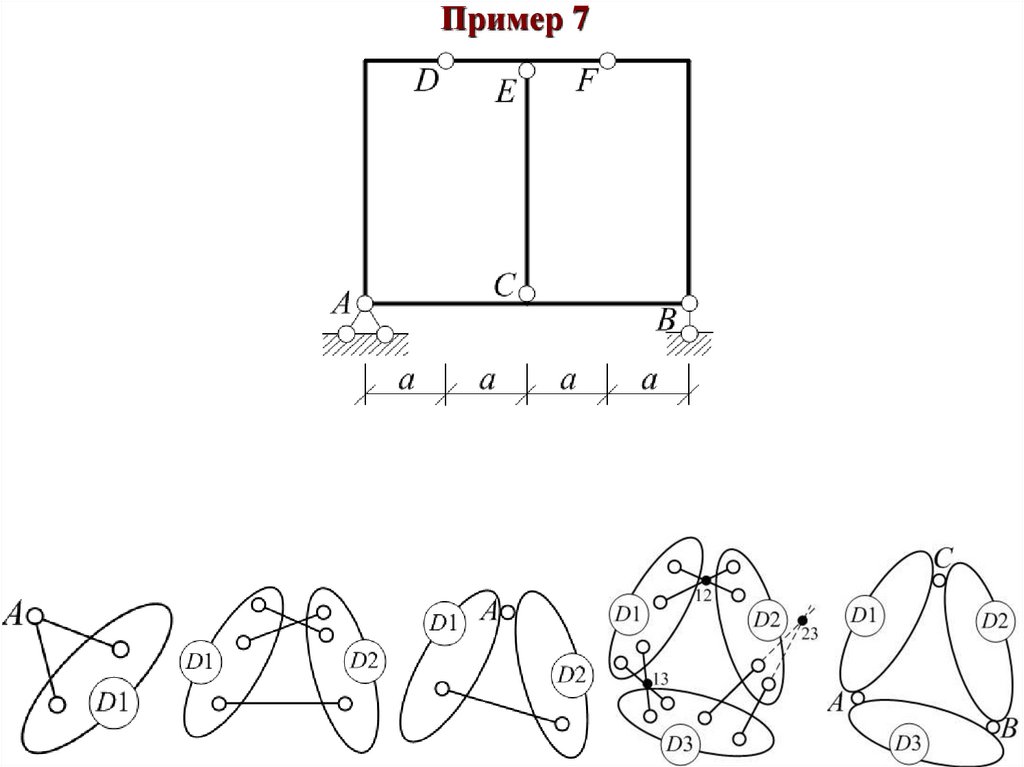
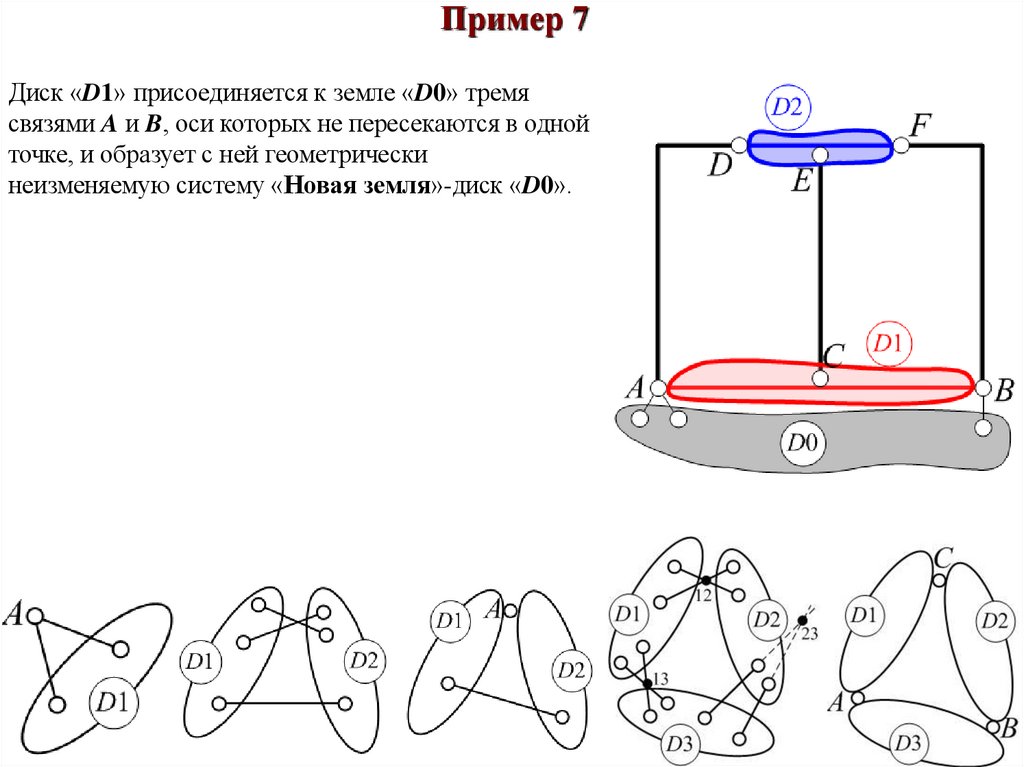
Пример 7Диск «D1» присоединяется к земле «D0» тремя
связями A и B, оси которых не пересекаются в одной
точке, и образует с ней геометрически
неизменяемую систему «Новая земля»-диск «D0».
62.
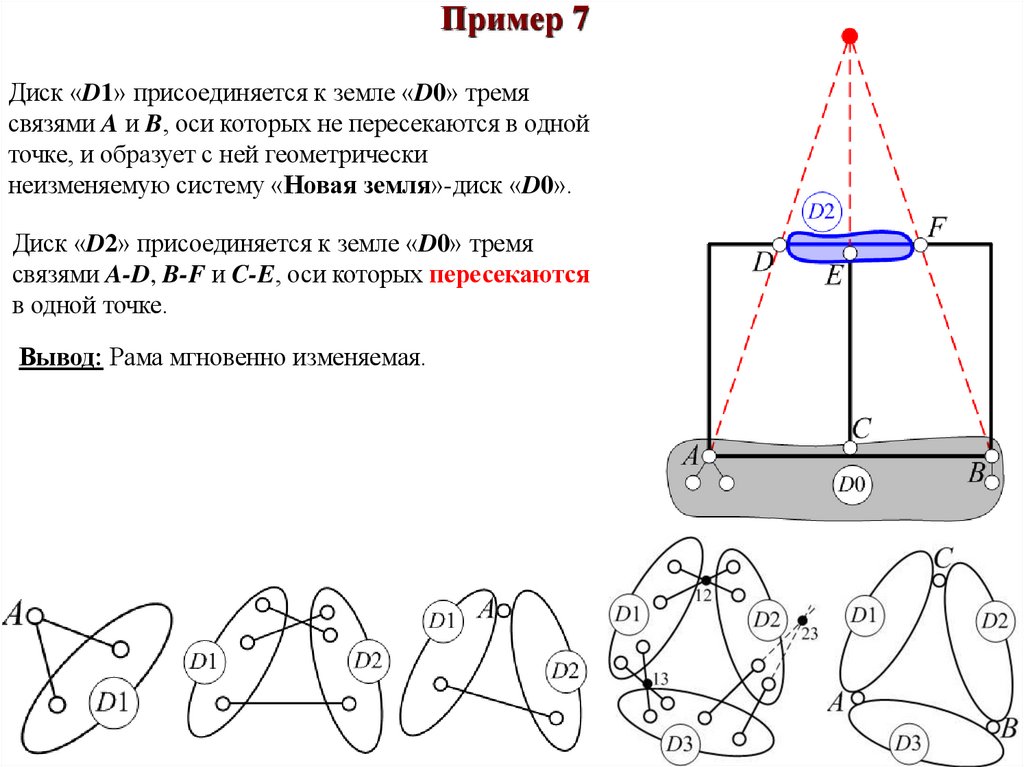
Пример 7Диск «D1» присоединяется к земле «D0» тремя
связями A и B, оси которых не пересекаются в одной
точке, и образует с ней геометрически
неизменяемую систему «Новая земля»-диск «D0».
Диск «D2» присоединяется к земле «D0» тремя
связями A-D, B-F и C-E, оси которых пересекаются
в одной точке.
Вывод: Рама мгновенно изменяемая.
63.
Конец лекции64. Типы связей плоских систем
Типсвязи
Наименование
связи
1
2
Изображение
связи на
расчетной
схеме
3
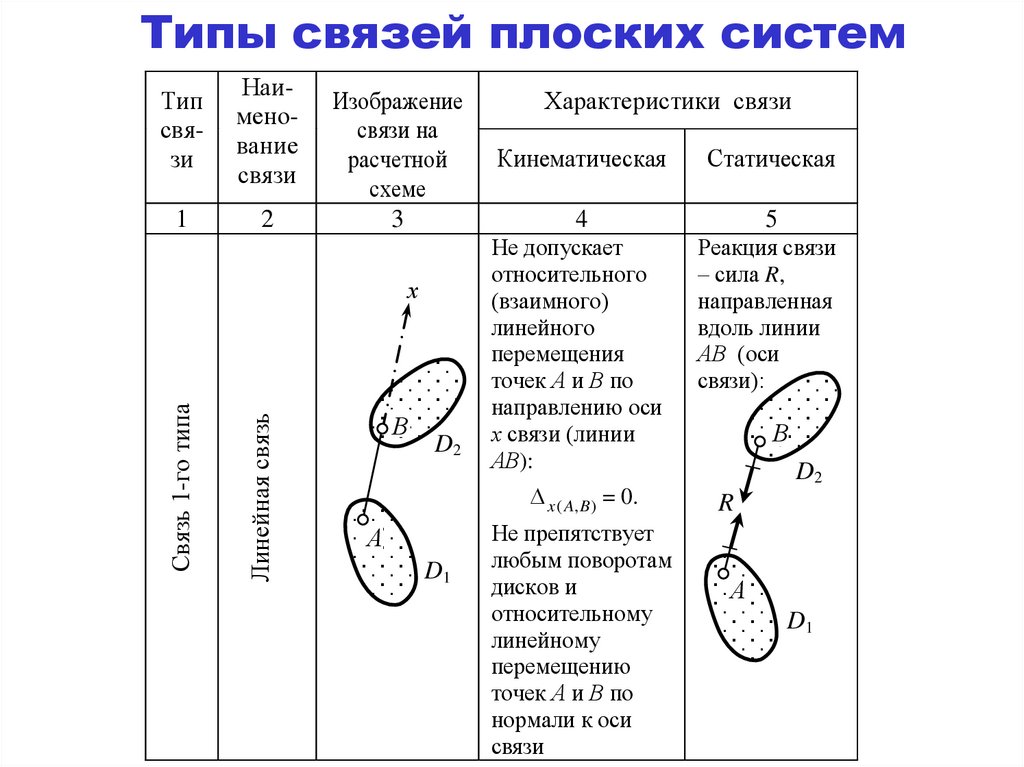
Линейная связь
Связь 1-го типа
х
В
D2
Характеристики связи
Кинематическая
Статическая
4
5
Не допускает
относительного
(взаимного)
линейного
перемещения
точек А и В по
направлению оси
х связи (линии
АВ):
Реакция связи
– сила R,
направленная
вдоль линии
АВ (оси
связи):
x ( A, B ) = 0.
А
D1
Не препятствует
любым поворотам
дисков и
относительному
линейному
перемещению
точек А и В по
нормали к оси
связи
В
D2
R
А
D1
65.
66. Свойства статически определимых систем
67.
68.
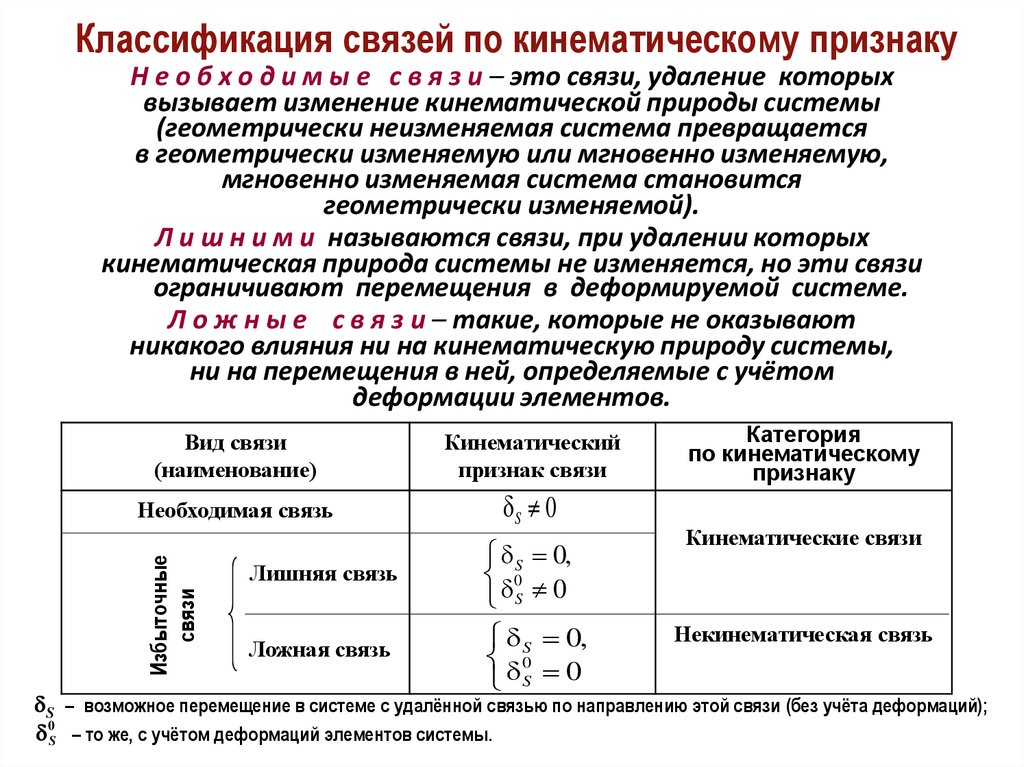
Классификация связей по кинематическому признакуВид связи
(наименование)
Кинематический
признак связи
Необходимая связь
S 0
Избыточные
связи
Н е о б х о д и м ы е с в я з и – это связи, удаление которых
вызывает изменение кинематической природы системы
(геометрически неизменяемая система превращается
в геометрически изменяемую или мгновенно изменяемую,
мгновенно изменяемая система становится
геометрически изменяемой).
Л и ш н и м и называются связи, при удалении которых
кинематическая природа системы не изменяется, но эти связи
ограничивают перемещения в деформируемой системе.
Л о ж н ы е с в я з и – такие, которые не оказывают
никакого влияния ни на кинематическую природу системы,
ни на перемещения в ней, определяемые с учётом
деформации элементов.
S 0,
0 0
S
S 0,
0 0
S
Лишняя связь
Ложная связь
Категория
по кинематическому
признаку
Кинематические связи
Некинематическая связь
S – возможное перемещение в системе с удалённой связью по направлению этой связи (без учёта деформаций);
0S – то же, с учётом деформаций элементов системы.
69. Д и с к и
Дискиа)
б)
е)
в)
г)
ж)
и)
д)
з)
к)
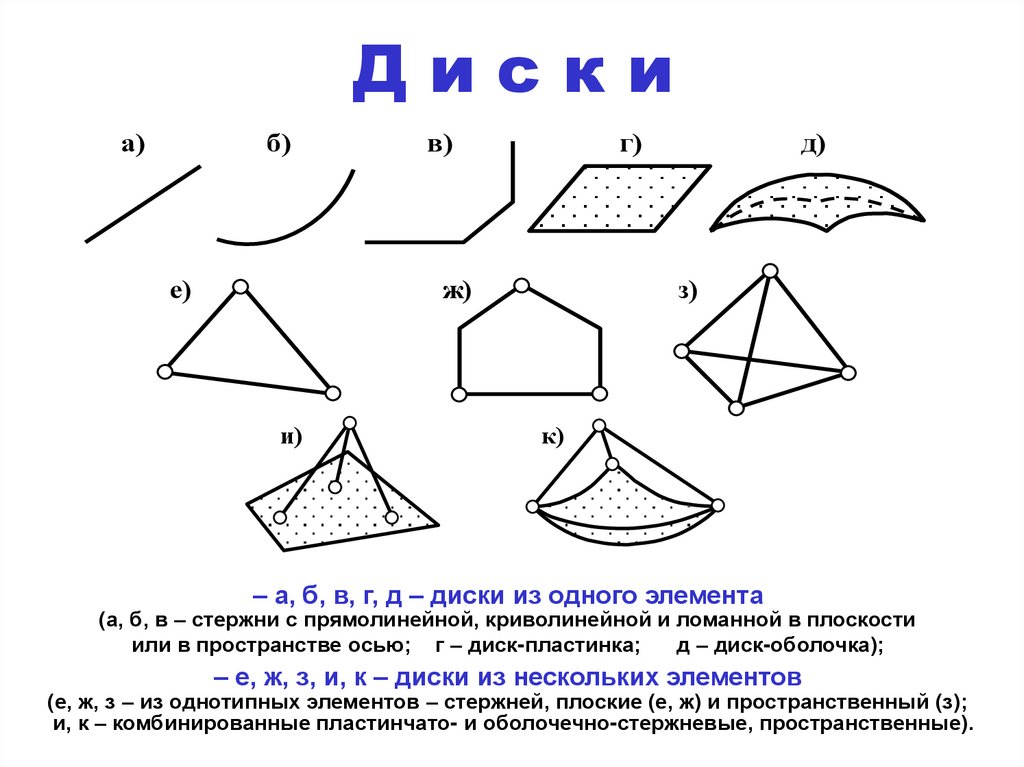
– а, б, в, г, д – диски из одного элемента
(а, б, в – стержни с прямолинейной, криволинейной и ломанной в плоскости
или в пространстве осью; г – диск-пластинка;
д – диск-оболочка);
– е, ж, з, и, к – диски из нескольких элементов
(е, ж, з – из однотипных элементов – стержней, плоские (е, ж) и пространственный (з);
и, к – комбинированные пластинчато- и оболочечно-стержневые, пространственные).
70. Классификация связей
– по соединяемым дискамдискретные (в отдельных точках или
сечениях)
континуальные (распределённые по объёму,
поверхности или линии)
внутренние
внешние
– по числу ограничиваемых
перемещений
простые (линейные и угловые)
сложные
– по физическим свойствам
жёсткие (недеформируемые)
податливые (деформируемые)
– по кинематическому
признаку
необходимые
избыточные (лишние и ложные)
– по области расположения
71. Типы связей плоских систем
Типсвя-зи
Наименование
связи
1
Изображение
связи на
расчетной схеме
2
3
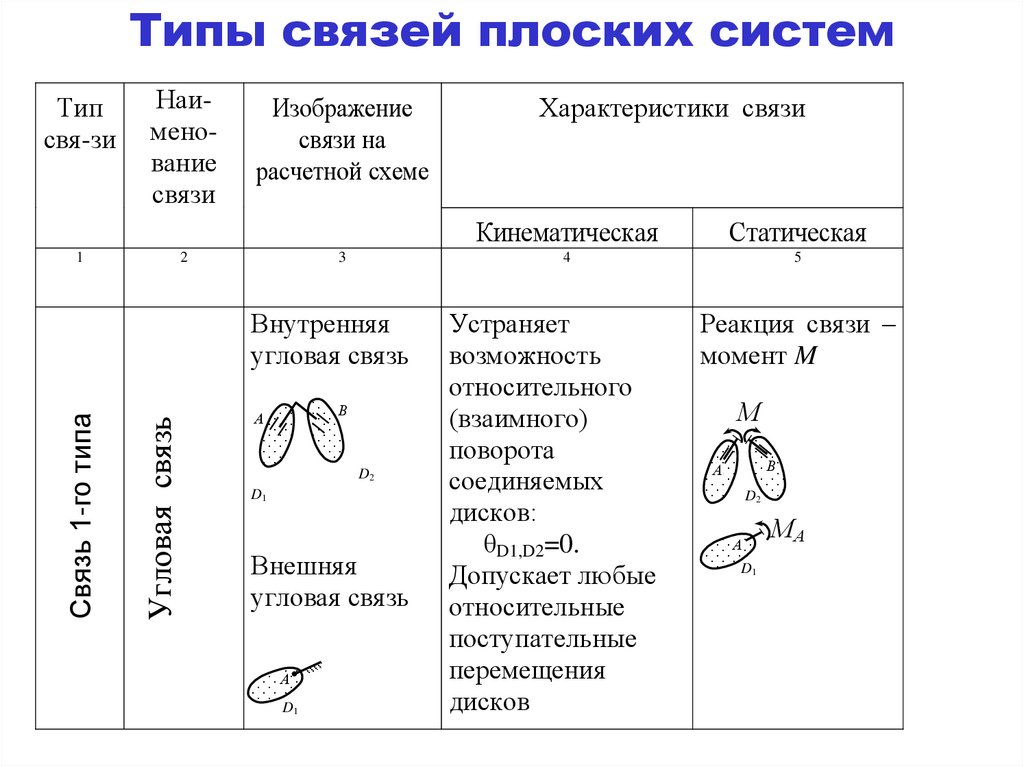
Угловая связь
Связь 1-го типа
Внутренняя
угловая связь
В
А
D2
D1
Внешняя
угловая связь
А
D1
Характеристики связи
Кинематическая
Статическая
4
5
Устраняет
возможность
относительного
(взаимного)
поворота
соединяемых
дисков:
θD1,D2=0.
Допускает любые
относительные
поступательные
перемещения
дисков
Реакция связи –
момент M
М
В
А
D2
А
D1
МА
72.
Цилиндрический шарнир2
3
4
5
Не допускает относительного
(взаимного) линейного
перемещения точек С1 и С2 дисков
D
1 и 2, совпадающих с шарниром
у
С, по любому направлению ( = С R R
х
С
С
D
С
С 0)
R
D
или,
в
проекциях
на
произвольные
R
D
D
оси х и у:
R R ;
С
Реакция связи – сила RС по
направлению, требующему
определения расчетом, или
ее составляющие RСх и RСу
RC1 у
С
D1
2
1
С C1 x
1
С1 ,С 2
1
2
2
C2 x
1
2
C2 у
2
ds
D1
C1 x
х (С1 ,С2 ) 0,
C2 x
RC1 y RC2 y .
у (С1 ,С2 ) 0.
Не препятствует любым взаимным
поворотам дисков вокруг точки С
у
D
Реакции связи – cила R ,
Устраняет возможность
нормальная
А
к оси связи,
относительного (взаимного)
и момент М
D
поворота соединяемых дисков и
В
М R
х относительного линейного
D
D
у перемещения
точек А и В по
А
А
М
D направлению нормали у к оси х
В
В
D
R
D
у связи (линии АВ):
А
D2
1
Поступательный шарнир
Связь 2-го типа (шарнир)
1
y
2
A
Aу
1
1
B
2
Bу
1
В
D1
D1
D2
D1 , D2 0,
y ( A, B ) 0.
Допускает относительное
линейное перемещение точек А и
В вдоль оси х связи
2
RAy RBy ;
M A M B.
73. Типы связей плоских систем
Типсвязи
Наименование
связи
Изображение
связи
на расчетной
схеме
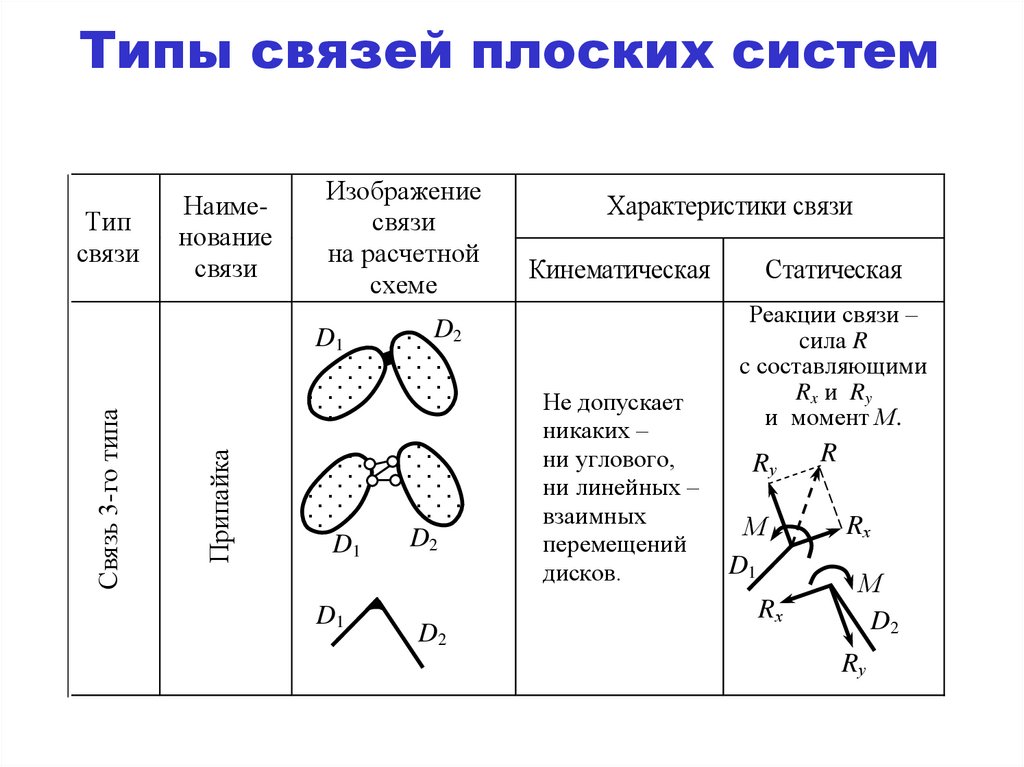
Припайка
Связь 3-го типа
D1
D1
D1
Характеристики связи
Кинематическая
D2
D2
D2
Не допускает
никаких –
ни углового,
ни линейных –
взаимных
перемещений
дисков.
Статическая
Реакции связи –
cила R
c составляющими
Rx и Ry
и момент М.
Rу
М
D1
Rх
R
Rх
М
D2
Rу
74. Этапы кинематического анализа
1) количественный анализ;2) качественный (структурный) анализ.
К о л и ч е с т в е н н ы й а н а л и з–
это исследование расчётной схемы сооружения,
заключающееся в оценке
W = n – nc
разности суммарного числа nΔ степеней
свободы дисков системы до наложения на них
внешних и внутренних связей (т.е. несвязанных
дисков) и суммарного числа nc внешних и внутренних
связей системы, в пересчёте на связи первого
типа.
Необходимое условие
геометрической неизменяемости системы:
W 0
75.
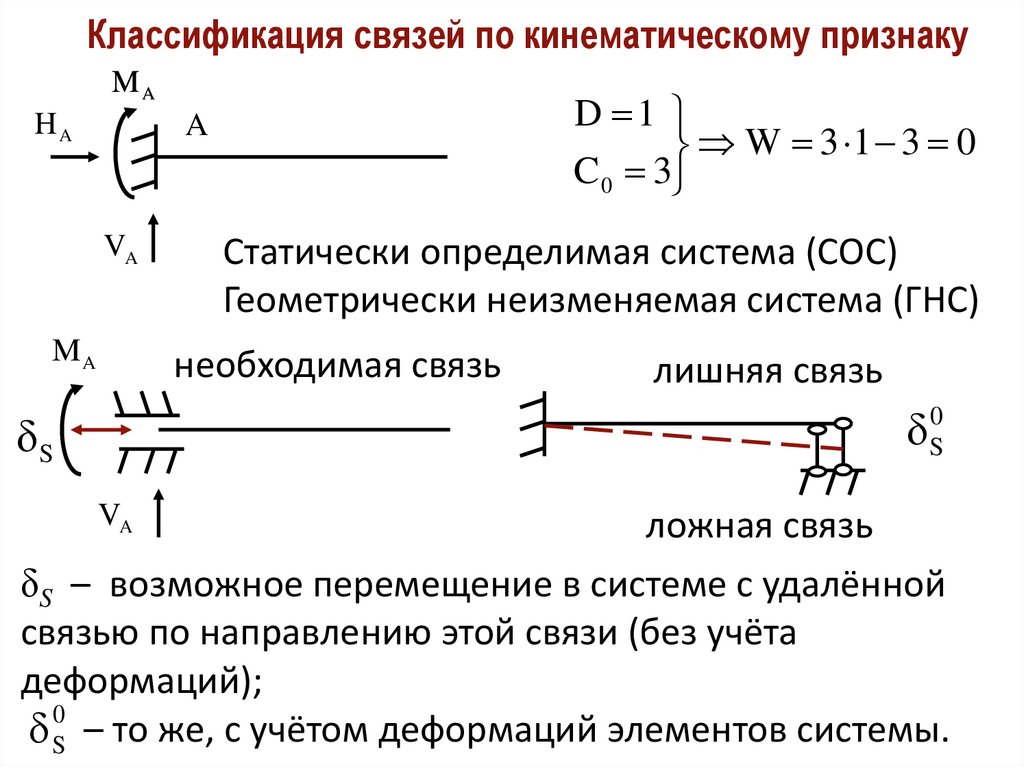
Классификация связей по кинематическому признакуMA
HA
D 1
W 3 1 3 0
C 0 3
A
VA
MA
Статически определимая система (СОС)
Геометрически неизменяемая система (ГНС)
необходимая связь
лишняя связь
S
VA
0
S
ложная связь
δS – возможное перемещение в системе с удалённой
связью по направлению этой связи (без учёта
деформаций);
0
S – то же, с учётом деформаций элементов системы.
76.
Второстепенные части могут образовыватьиерархию по признаку большей-меньшей
второстепенности. Самой второстепенной
частью является та, которая неработоспособна
при отсутствии любой другой части системы.
Практическая рекомендация по последовательности
расчёта статически определимой составной
системы: для определения реакций связей
рассматривается равновесие частей, начиная с
самой второстепенной и заканчивая главной
(то есть в порядке, обратном последовательности
синтеза).
Замечание: понятия составной системы,
главной и второстепенной частей, а также
соображения о последовательности расчёта не
относятся непосредственно к
кинематическому анализу ; принципиально
важными они являются для статически
определимых систем.
77.
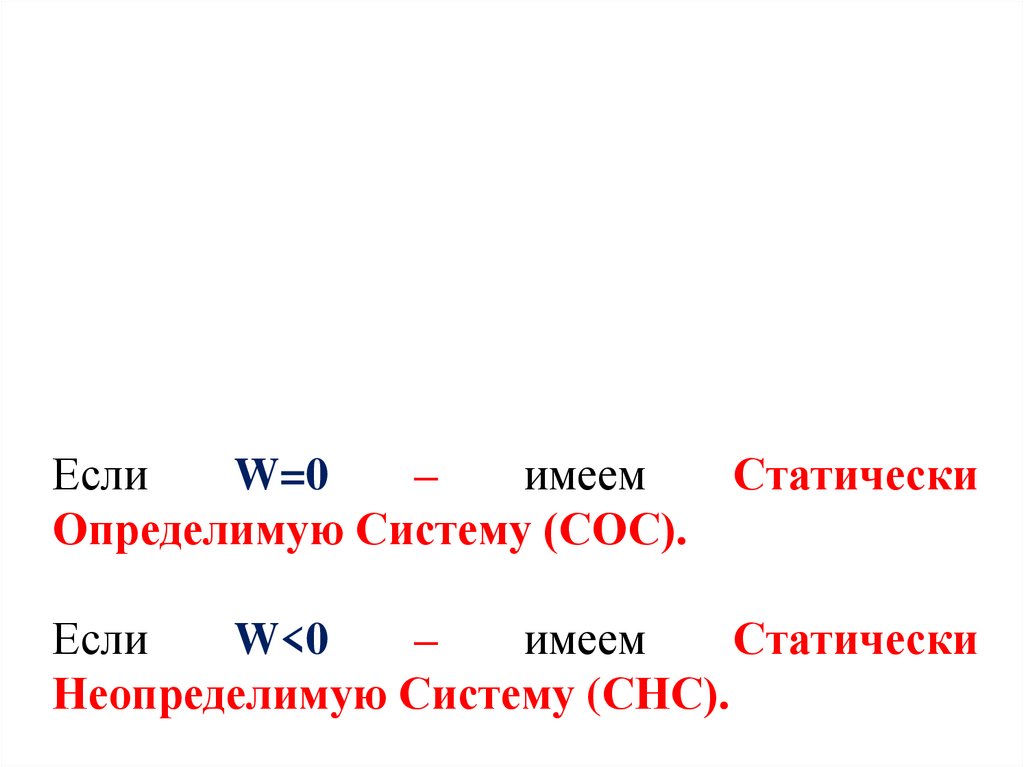
ЕслиW=0
–
имеем
Статически
Определимую Систему (СОС).
Если
W<0
–
имеем
Статически
Неопределимую Систему (СНС).
78.
Необходимое (но не достаточное) условиегеометрической неизменяемости системы:
W≤0
W = nΔ – nC
Для плоских ферм:
W = 2У –(С+С0 ) ≤ 0.
У – количество узлов, С – количество
стержней системы, С0 – количество опорных
связей.





























 mechanics
mechanics








