Частотная передаточная функция и частотные характеристики

1. Частотная передаточная функция и частотные характеристики

2. Определения частотных характеристик

0
x t X msin t
X j
W j
y t Ymsin( t )
Y j
Амплитудная частотная характеристика (АЧХ)
A
Фазовая частотная характеристика (ФЧХ)
Xm
Ym
Амплитудно-фазовая частотная характеристика
j
(АФЧХ или АФХ)
W j A e
W j W p p j
Графики АЧХ и ФЧХ один под другим в западной
литературе называется диаграммой Боде

3. Амплитудно-фазовая ха­рактеристика

Амплитудно-фазовая характеристика
АФХ в общем виде
показательная форма АФХ
алгебраическая форма АФХ
тригонометрическая
форма АФХ
W j A e
W j k
bm j bm 1 j
m
an j an 1 j
j
W j Re W j j Im W j
W j P jQ
W j A cos jA sin
n
m 1
n 1
... 1
... 1
m n

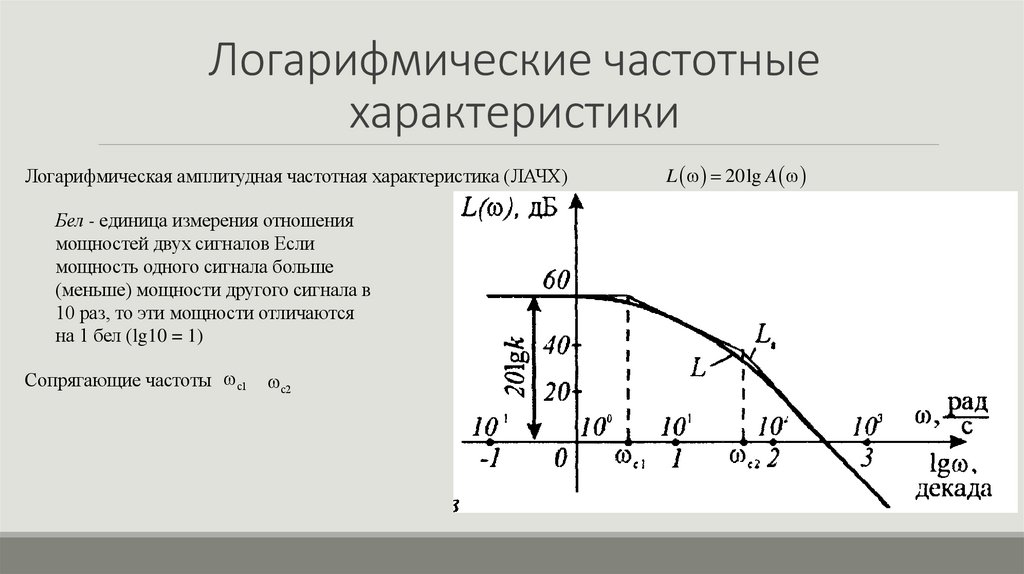
4. Логарифмические частотные характеристики

Логарифмическая амплитудная частотная характеристика (ЛАЧХ)
Бел - единица измерения отношения
мощностей двух сигналов Если
мощность одного сигнала больше
(меньше) мощности другого сигнала в
10 раз, то эти мощности отличаются
на 1 бел (lg10 = 1)
Сопрягающие частоты с1
с2
L 20lg A

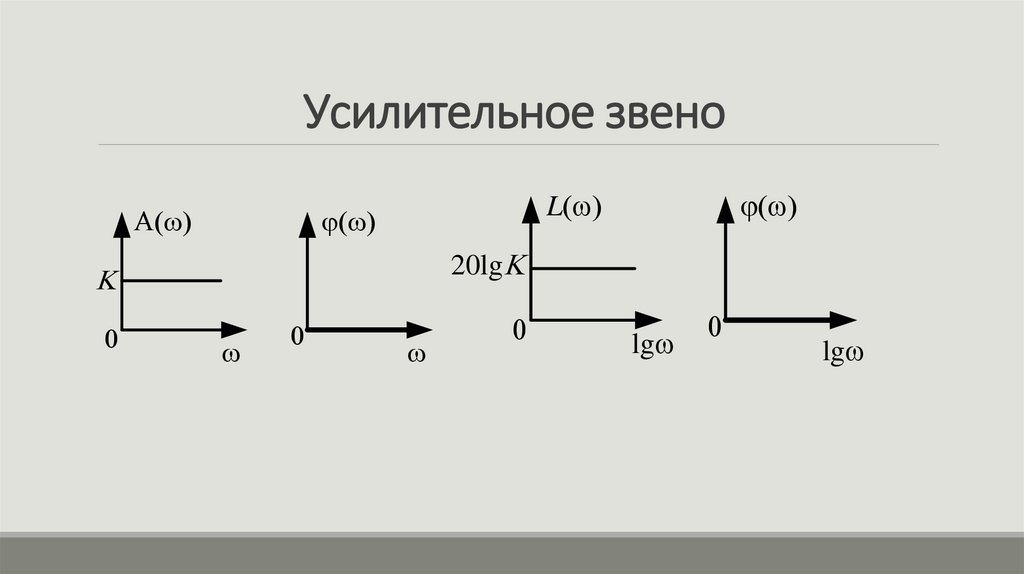
5. Усилительное звено

частотная передаточная функция
W ( j ) K
АЧХ
A( ) K
Действительная часть частотной
передаточной функции
P( ) K
Мнимая часть частотной передаточной
функции
Q( ) 0
ФЧХ
ЛЧХ
Q( )
( ) arctg
0.
P( )
L( ) 20lg K
ЛФЧХ
L ( ) 0

6. Усилительное звено

A
20lgK
K
0
L
0
0
lg
0
lg

7. Интегрирующее звено

частотная передаточная функция
Действительная часть частотной
передаточной функции
Мнимая часть частотной передаточной
функции
АЧХ
ФЧХ
ЛЧХ
ЛФЧХ
K
K K j 2
W ( j )
j e
j
P( ) 0
K
K
A( )
Q( )
K /
( ) arctg
arctg
2
0
P( )
Q( )
L( ) 20lg k 20lg .
L ( ) 20lg
2

8. Интегрирующее звено

0
АФЧХ
P(
0
АЧХ
0
2
L
ФЧХ
20lgk
A
jQ
-20 дБ/дек
0
lgk lg
ЛАЧХ

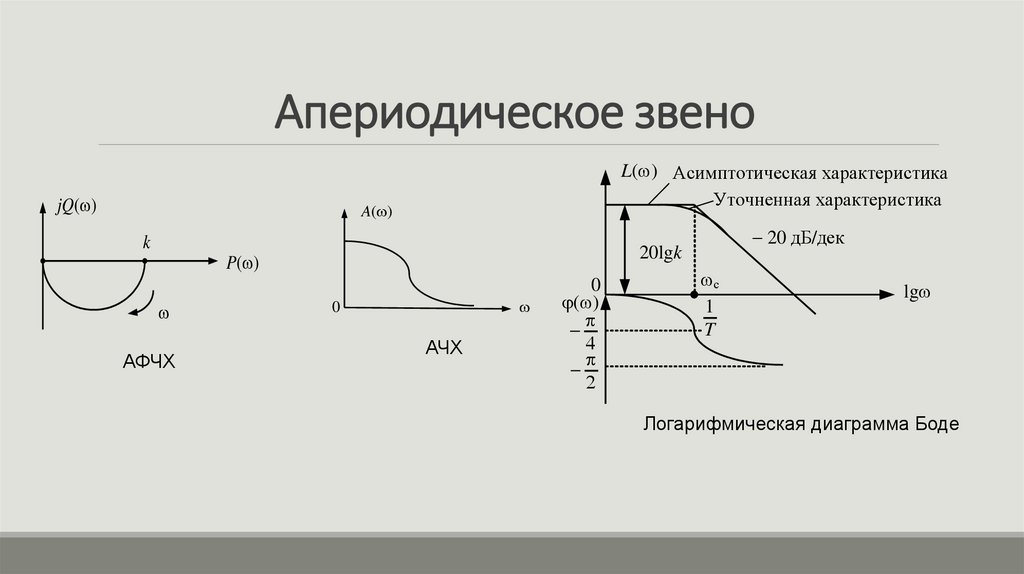
9. Апериодическое звено

частотная передаточная функция
АЧХ
Действительная часть частотной
передаточной функции
Мнимая часть частотной передаточной
функции
ФЧХ
ЛЧХ
W ( j )
k
k
kT
j
jT 1 1 T 2 2
1 T 2 2
k2
k 2T 2 2
k
A( )
(1 T 2 2 )2 (1 T 2 2 ) 2
1 T 2 2
k
P( )
1 T 2 2
kT
1 T 2 2
Q( )
( ) arctg
arctg T .
P( )
Q( )
L( ) 20lg k 20lg 1 T 2 2

10. Апериодическое звено

jQ( )
L( ) Асимптотическая характеристика
Уточненная характеристика
A( )
k
P( )
АФЧХ
20 дБ/дек
20lgk
0
АЧХ
0
( )
2
с
1
T
lg
Логарифмическая диаграмма Боде

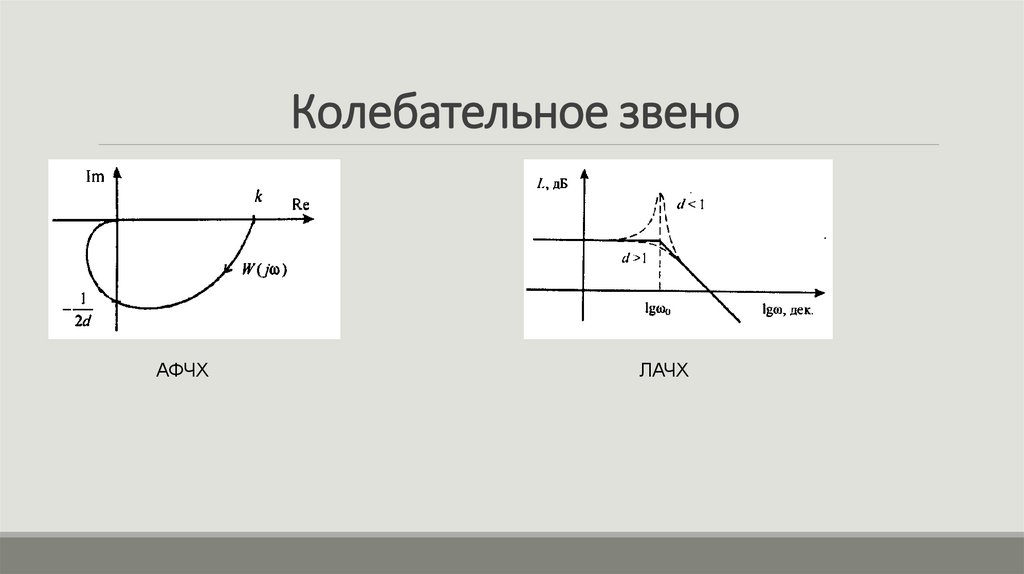
11. Колебательное звено

частотная передаточная функция
k 1 T 2 2 j 2kT
k
W ( j )
2 2
T j 2 T 1 1 T 2 2 2 4 2T 2 2
АЧХ
A( )
Действительная часть частотной
передаточной функции
Мнимая часть частотной передаточной
функции
ФЧХ
ЛЧХ
k
1 T 2 2 4 2T 2 2
2
P( )
Q ( )
k 1 T 2 2
1 T 2 2 4 2T 2 2
2
2kT
1 T 4 T
2
2
2
2
2
2
2 T
arctg
1 T 2 2
( )
arctg 2 T
1 T 2 2
L( ) 20lgk 20lg (1 T 2 2 ) 2 4 2T 2 2
при с ,
при c .
при c ,
20lgk
L( )
20lgk 40lgT при c .

12. Колебательное звено

АФЧХ
ЛАЧХ

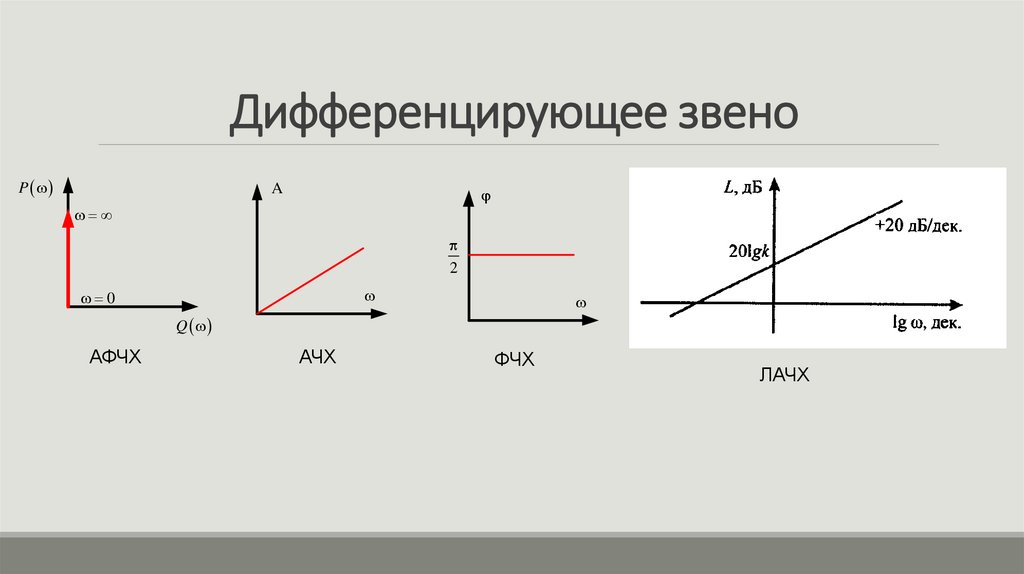
13. Дифференцирующее звено

частотная передаточная функция
W ( j ) jk
АЧХ
A( ) k
Действительная часть частотной
передаточной функции
P( ) 0
Мнимая часть частотной передаточной
функции
Q( ) k
ФЧХ
Q( )
( ) arctg
2.
P
(
)
ЛЧХ
L( ) 20lg k 20lg

14. Дифференцирующее звено

P
A
2
0
Q
АФЧХ
АЧХ
ФЧХ
ЛАЧХ

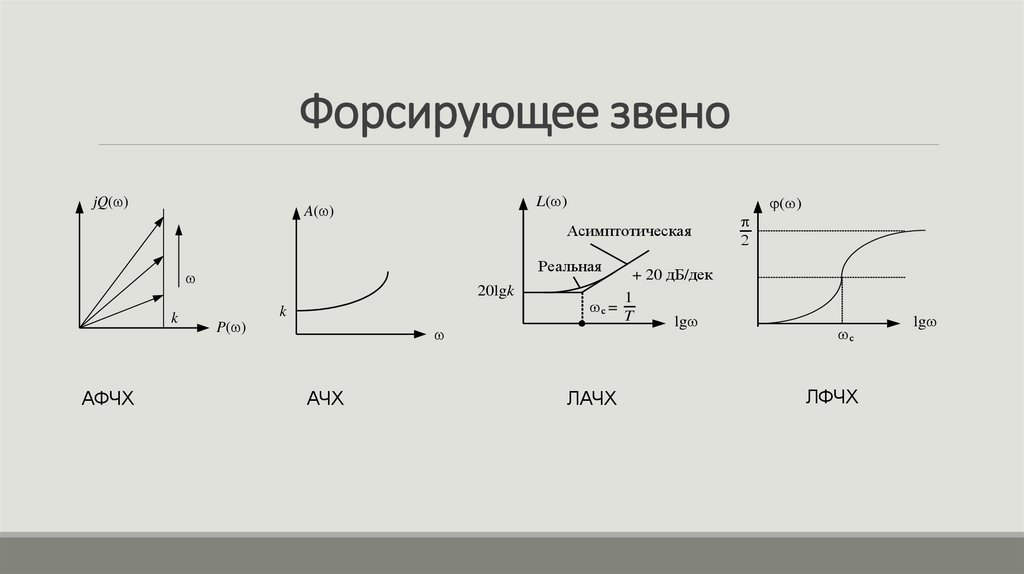
15. Форсирующее звено

частотная передаточная функция
АЧХ
W ( j ) k jkT
A( ) k
1 T
Действительная часть частотной
передаточной функции
P( ) k
Мнимая часть частотной передаточной
функции
Q( ) kT
ФЧХ
ЛЧХ
2
2
Q( )
( ) arctg
T .
P
(
)
при c ,
20lgk
L( ) 20lg k 20lg 1 T 2 2
20lgk 20lgT при c .

16. Форсирующее звено

jQ( )
L( )
A( )
Асимптотическая
Реальная
k
АФЧХ
2
( )
20lgk
k
P( )
АЧХ
+ 20 дБ/дек
1
с =
T
lg
ЛАЧХ
с
ЛФЧХ
lg

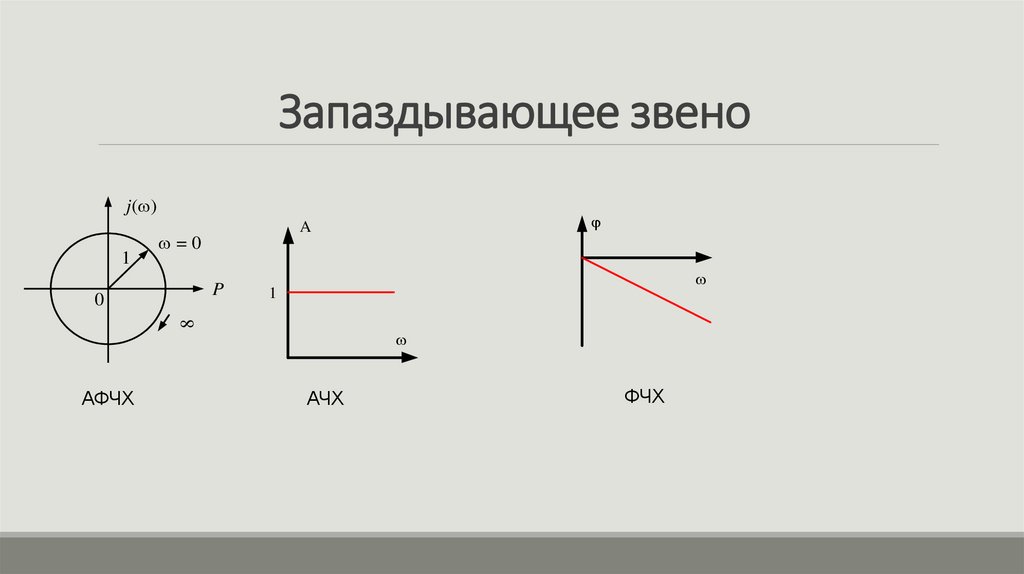
17. Запаздывающее звено

частотная передаточная функция
W ( j ) W ( j ) e j cos jsin
АЧХ
A( ) 1
Действительная часть частотной
передаточной функции
P( ) cos
Мнимая часть частотной передаточной
функции
Q( ) sin
ФЧХ
Q( )
( ) arctg
.
P
(
)
ЛЧХ
L( ) 20lg1 0

18. Запаздывающее звено

j( )
1
= 0
P
1
8
0
A
АФЧХ
АЧХ
ФЧХ