Выражения с переменными. Многочлены

1.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Числовое выражение — запись,
состоящая из чисел, знаков действий и скобок.
Определение. Значение числового выражения —
число, получающееся, если выполнить в данном
выражении все входящие в него действия.

2.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Числовые выражения, не имеющие смысла
(их значение не определено):
−5,
2
0
Определение. Числовым равенством
называется запись вида A=B (1),
где A и B — числовые выражения.

3.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
A=B (1)
Если хотя бы одно из выражений A и B не имеет смысла
(т. е. его значение не определено), то говорят, что
равенство (1) не имеет смысла.
Если же оба выражения A и B имеют смысл, то и
равенство (1) имеет смысл.
Если значения числовых выражений A и B равны, то
равенство(1) называют верным; в противном случае его
называют неверным.

4.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Выражение с переменными – это запись,
содержащая числа, знаки действий, скобки,
переменные, обозначенные буквами
Выражение с переменными х, у, …, z кратко
записывают в виде Р(х, у, …, z).

5.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Пусть переменные х, у, …, z принимают соответственные
значения х0, у0, …, z0.
Если числовое выражение Р(х0, у0, …, z0) имеет смысл
(все указанные в нем операции выполнимы), то набор
числовых значений называется допустимым.
Множество всех наборов числовых значений
переменных, допустимых для выражения Р(х, у, …, z),
называется областью определения этого выражения.

6.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
В курсе элементарной математики рассматриваются
выражения, которые называются элементарными.
1) х +2х +3; 2)
2
6) log2(x-7);
; 4) 3х у ; 5) 2sin
4 3
; 3)
7)
;
8)
; 9) 7
+11; 10)

7.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
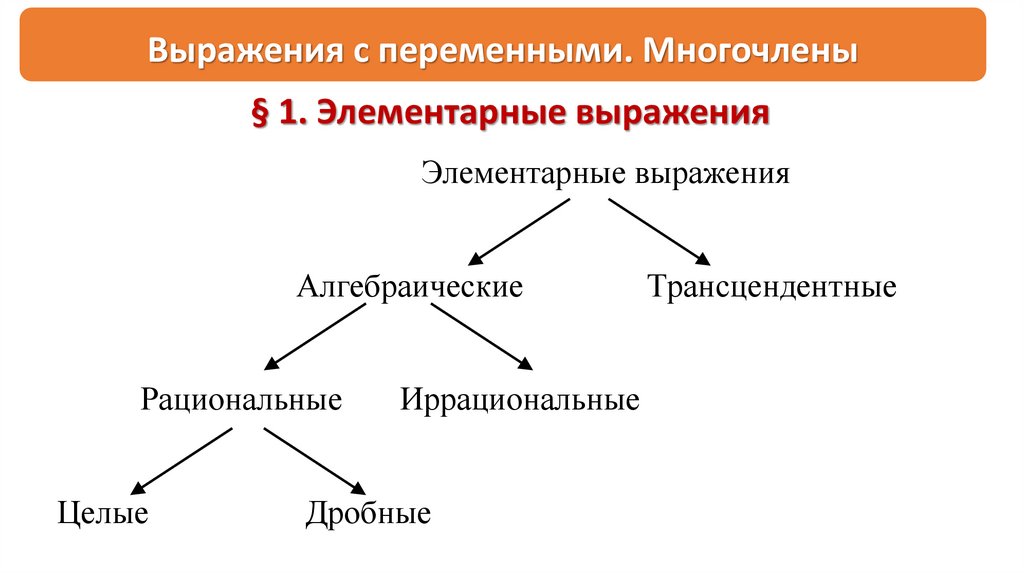
Элементарные выражения
Алгебраические
Рациональные
Целые
Иррациональные
Дробные
Трансцендентные

8.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Алгебраическое выражение − это
выражение, составленное из чисел и переменных с
помощью знаков сложения, вычитания, умножения,
деления, возведения в рациональную степень и
извлечения корня и скобок.
(1-4, 9-10)

9.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Если выражение содержит действия
возведения в иррациональную степень, взятие
логарифма, тригонометрической функции и обратной
тригонометрической функции, то оно называется
трансцендентным
(5-8)

10.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. В рациональных выражениях
используются только сложение, умножение,
вычитание, деление, возведение в степень с целым
показателем (сводится к умножению или делению).
(1, 4, 10)

11.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Иррациональное выражение
содержит извлечение корня.
(2, 3, 9)

12.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Целое рациональное выражение не
содержит деления на выражения с переменными
(деление на параметры допускается).
(1,4)

13.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Дробное рациональное выражение
содержит деление на выражение с переменными.
(10)

14.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Многочленом n-й степени
относительно переменной х называется выражение
вида
n
anx + an-1x
n-1
+ …+ a1x+ a0,
где an 0, n 0, ai – коэффициенты многочлена,
an – старший коэффициент, a0 – свободный член.
Многочлен является целым рациональным выражением!

15.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
Определение. Многочленом относительно
переменных х, у, …, z называется сумма
произведений вида
axn y m … zk, где а – числовой коэффициент,
n, m, …, k –неотрицательные целые числа.
Само выражение axn y m … zk называется одночленом.
Число n+m+…+k – степень одночлена.

16.

Выражения с переменными. Многочлены
§ 1. Элементарные выражения
5a(74a ) 4xy (−3xz)
a+b
Наибольшая из степеней одночленов, входящих в
многочлен, называется степенью многочлена.
Два одночлена называются подобными, если они
совпадают или же отличаются только числовыми
коэффициентами.
Стандартным (каноническим) видом многочлена
называется многочлен, заданный в виде суммы
попарно неподобных одночленов.
3
2

17.

Выражения с переменными. Многочлены
§ 2. Тождественные преобразования выражений
Определение. Алгебраическим равенством называется
запись вида A=B, где A и B — алгебраические выражения.
При подстановке в алгебраическое выражение некоторых
чисел в качестве значений переменных получится числовое
выражение.
Это значение называется числовым значением
алгебраического выражения при данных значениях
переменных.
Для алгебраического равенства нельзя определить,
является ли это равенство верным или нет!

18.

Выражения с переменными. Многочлены
§ 2. Тождественные преобразования выражений
Определение. Два алгебраических выражения
называются тождественно равными, если
• они определены на одном и том же множестве
значений переменных
• и принимают равные числовые значения при всех
допустимых значениях переменных, входящих в них.
1) Выражения 3+x2-2 и x2+1
2) Выражения 2(x+5) и 2x+10
3) Выражения x и x2/х

19.

Выражения с переменными. Многочлены
§ 2. Тождественные преобразования выражений
Определение. Тождество — алгебраическое
равенство, правая и левая части которого
тождественно равны.
(a+b)(a+c)=a2+ab+ac+bc
Определение. Тождественное преобразование
алгебраического выражения — замена этого
выражения другим, тождественно равным ему.

20.

Выражения с переменными. Многочлены
§ 3. Метод неопределенных коэффициентов
Метод применяется в тех случаях, когда заранее
известно, к какому виду требуется свести данное
выражение.
Коэффициенты искомого выражения
обозначаются буквами (А,В,С, …) и их рассматривают
как неизвестные.
Коэффициенты заданного и искомого выражения
приравниваются.

21.

Выражения с переменными. Многочлены
§ 3. Метод неопределенных коэффициентов
Пример 1. Многочлен х3+6х2+4х+6
расположить по степеням (х-1).
Решение.
х3+6х2+4х+6=А(х-1)3+В(х-1)2+С(х-1)+D
Подставим x=1 => D=17.
Подставим x=0, x= -1, x=2

22.

Выражения с переменными. Многочлены
§ 3. Метод неопределенных коэффициентов
Решение.
х3+6х2+4х+6=А(х-1)3+В(х-1)2+С(х-1)+D
x=0, x= -1, x=2