Пример решения задач симплекс-методом

1.

Пример решения задач
симплекс – методом

2. Пример

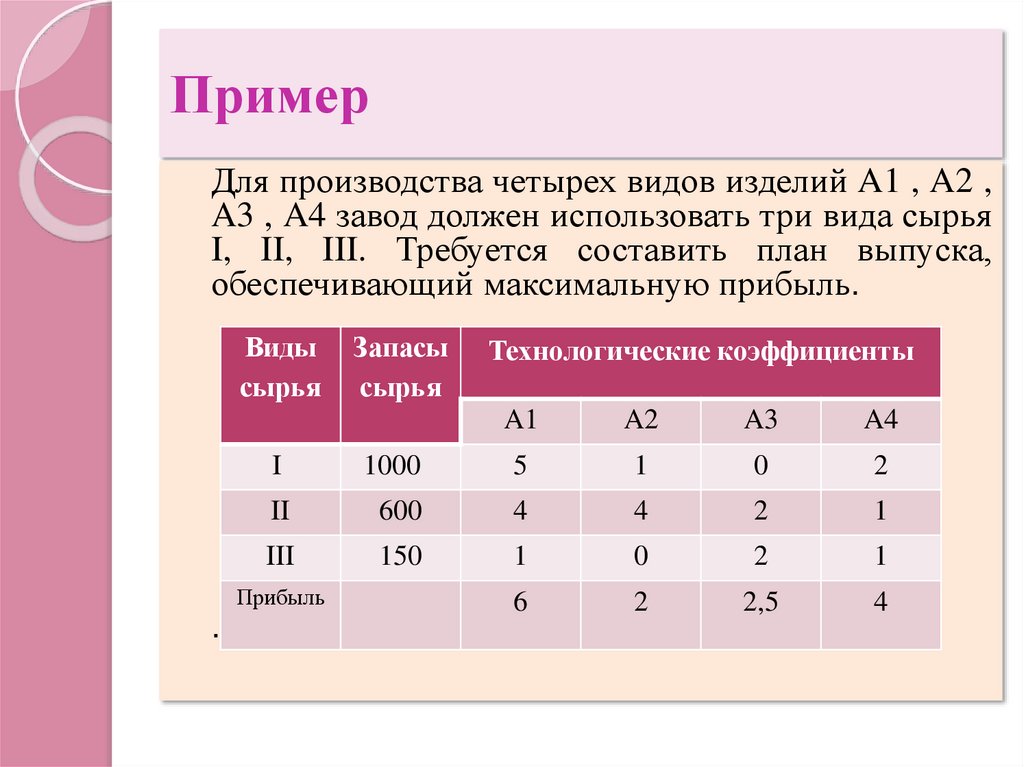
Для производства четырех видов изделий A1 , A2 ,
A3 , A4 завод должен использовать три вида сырья
I, II, III. Требуется составить план выпуска,
обеспечивающий максимальную прибыль.
Виды
сырья
Технологические коэффициенты
A1
A2
A3
A4
I
1000
5
1
0
2
II
600
4
4
2
1
III
150
1
0
2
1
6
2
2,5
4
Прибыль
.
Запасы
сырья

3. Пример

Математическая модель задачи:
.

4. Пример

Приведение задачи к каноническому виду:
Примем за базисные переменные x5, x6, x7.
Тогда опорное решение: (0; 0; 0; 0; 1000; 600; 150).

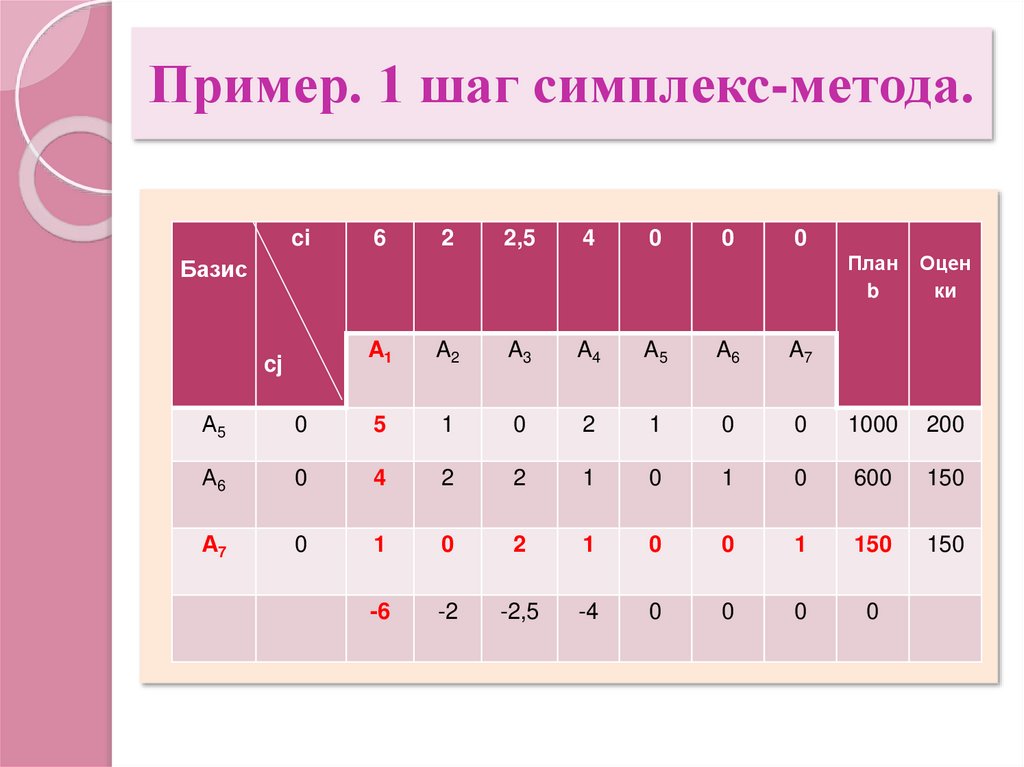
5. Пример. 1 шаг симплекс-метода.

ci
6
2
2,5
4
0
0
0
Базис
cj
A1
A2
A3
A4
A5
A6
A7
План
b
Оцен
ки
А5
0
5
1
0
2
1
0
0
1000
200
А6
0
4
2
2
1
0
1
0
600
150
А7
0
1
0
2
1
0
0
1
150
150
-6
-2
-2,5
-4
0
0
0
0

6. Подробный расчет 1 шага

А5
А6
А7
J

7. Пример. 1 шаг симплекс-метода

Базисное решение (0; 0; 0; 0; 1000; 600;
150).
Поиск ключевой строки (оценки Qi) :
min{
1000 600 150
;
;
} 150
5
4
1
Выводим из базиса переменную x7 и
вводим переменную x1

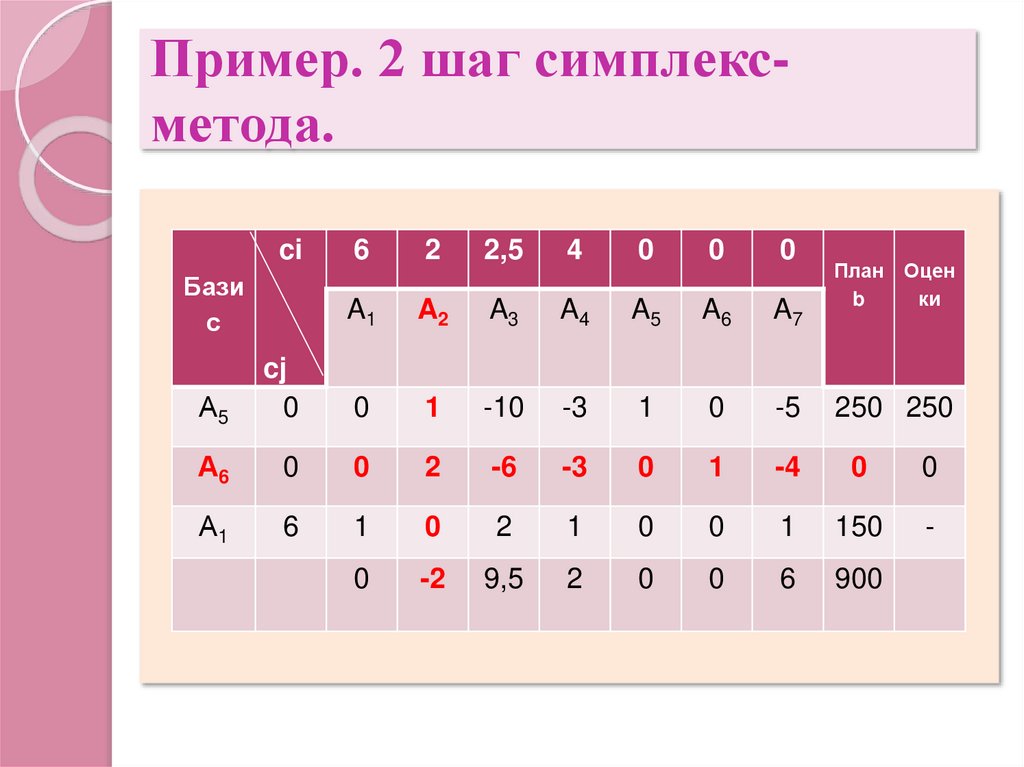
8. Пример. 2 шаг симплекс-метода.

Пример. 2 шаг симплексметода.
ci
6
2
2,5
4
0
0
0
A1
A2
A3
A4
A5
A6
A7
А5
cj
0
0
1
-10
-3
1
0
-5
250 250
А6
0
0
2
-6
-3
0
1
-4
0
0
А1
6
1
0
2
1
0
0
1
150
-
0
-2
9,5
2
0
0
6
900
Бази
с
План
b
Оцен
ки

9. Пример. 2 шаг симплекс-метода

Базисное решение (150; 0; 0; 0; 250; 0; 0).
Определение ключевой строки(оценки Qi):
0 250
min{ ;
} 0
2 1
Выводим из базиса переменную x6 и
вводим переменную x2.

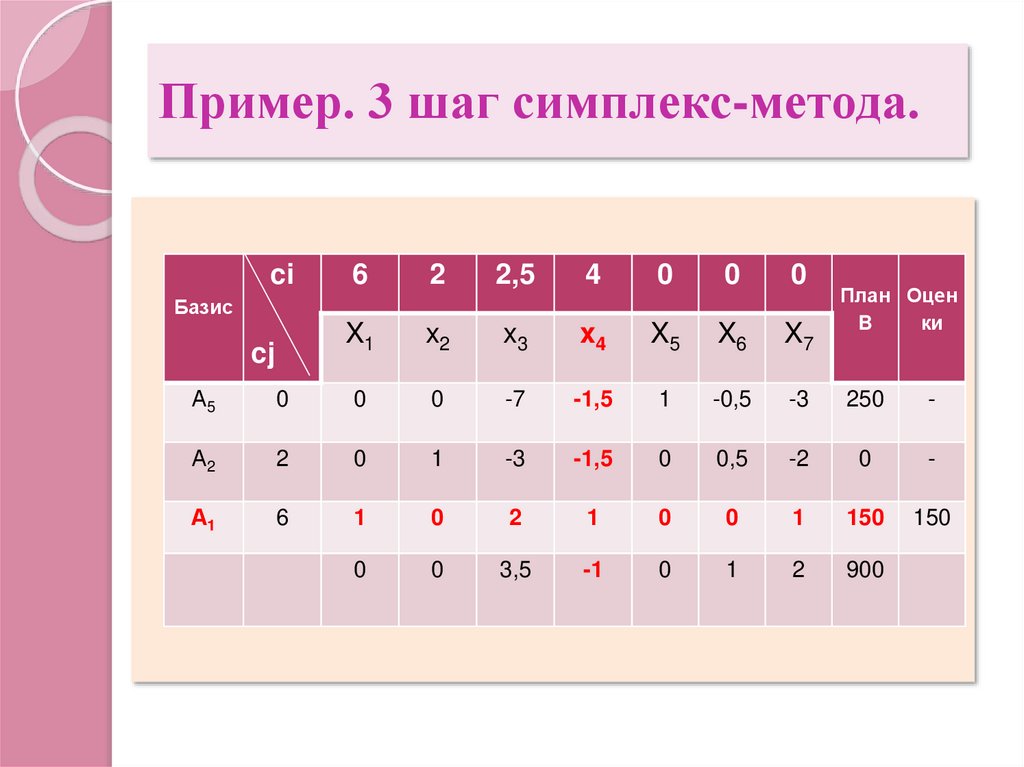
10. Пример. 3 шаг симплекс-метода.

ci
6
2
2,5
4
0
0
0
X1
x2
x3
x4
X5
X6
X7
Базис
cj
План Оцен
B
ки
А5
0
0
0
-7
-1,5
1
-0,5
-3
250
-
А2
2
0
1
-3
-1,5
0
0,5
-2
0
-
А1
6
1
0
2
1
0
0
1
150
150
0
0
3,5
-1
0
1
2
900

11. Пример. 3 шаг симплекс-метода

Базисное решение (150; 0; 0; 0; 250; 0; 0).
Определение ключевой строки (оценки Qi) :
150
min{
} 150
1
Выводим из базиса переменную x1 и вводим
переменную x4.

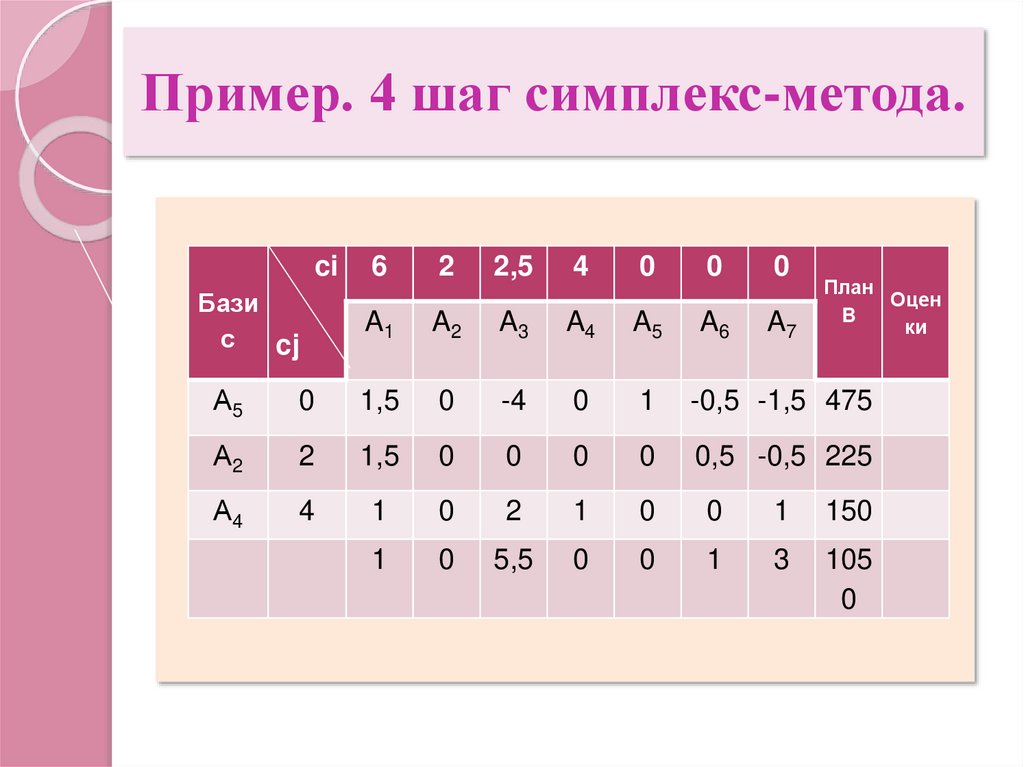
12. Пример. 4 шаг симплекс-метода.

ci
6
2
2,5
4
0
0
0
Бази
с
cj
A1
A2
A3
A4
A5
A6
A7
А5
0
1,5
0
-4
0
1
-0,5 -1,5 475
А2
2
1,5
0
0
0
0
0,5 -0,5 225
А4
4
1
0
2
1
0
0
1
150
1
0
5,5
0
0
1
3
105
0
План
Оцен
B
ки

13. Пример. 4 шаг симплекс-метода

Оптимальное решение:
(0; 225; 0; 150; 475; 0; 0),
при котором Fmax = 1050.
То есть, для получения наибольшей
прибыли, равной 1050 денежных единиц,
предприятие должно выпустить 225 единиц
продукции вида A2, 150 единиц продукции
вида A4. Продукцию вида A1 и A3
производить не выгодно. При этом сырье
типа II и III будет использовано полностью, а
475 единиц сырья типа I останутся
неизрасходованными.

14. Метод искусственного базиса

15. Пример

Исходная задача:
F ( x) 4 x1 4 x2 2 x3
2 x1 x2 x3 1
2 x1 x2 2 x3 2
x1, 2,3 0

16. Пример

М-задача:
F ( x) 4 x1 4 x2 2 x3 Mx4 Mx5
2 x1 x2 x3 x4 1
2 x1 x2 2 x3 x5 2
x1, 2,3, 4,5 0

17. Пример

М-задача с преобразованной целевой
функцией:
( 4M 4) x1 4 x2 ( 3M 2) x3 3M F ( x)
2 x1 x2 x3 x4 1
2 x1 x2 2 x3 x5 2
x1, 2,3, 4,5 0

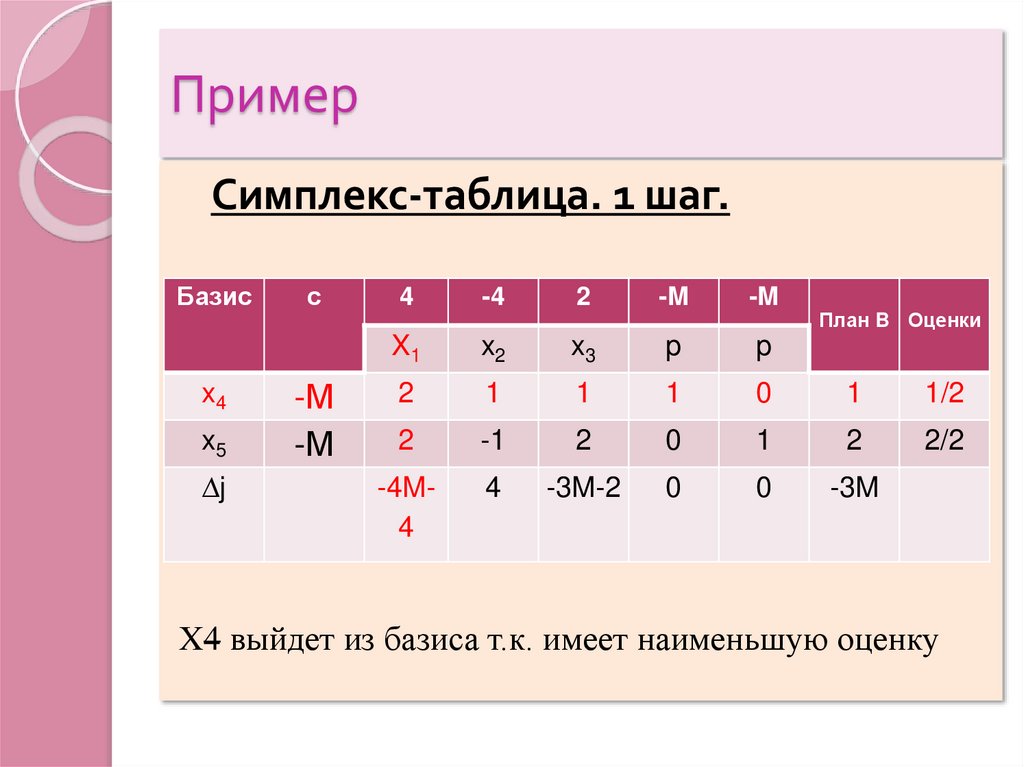
18. Пример

Симплекс-таблица. 1 шаг.
Базис
x4
x5
∆j
с
-М
-М
4
-4
2
-M
-M
X1
x2
x3
p
p
2
1
1
1
0
1
1/2
2
-1
2
0
1
2
2/2
-4M4
4
-3M-2
0
0
-3M
План B Оценки
X4 выйдет из базиса т.к. имеет наименьшую оценку

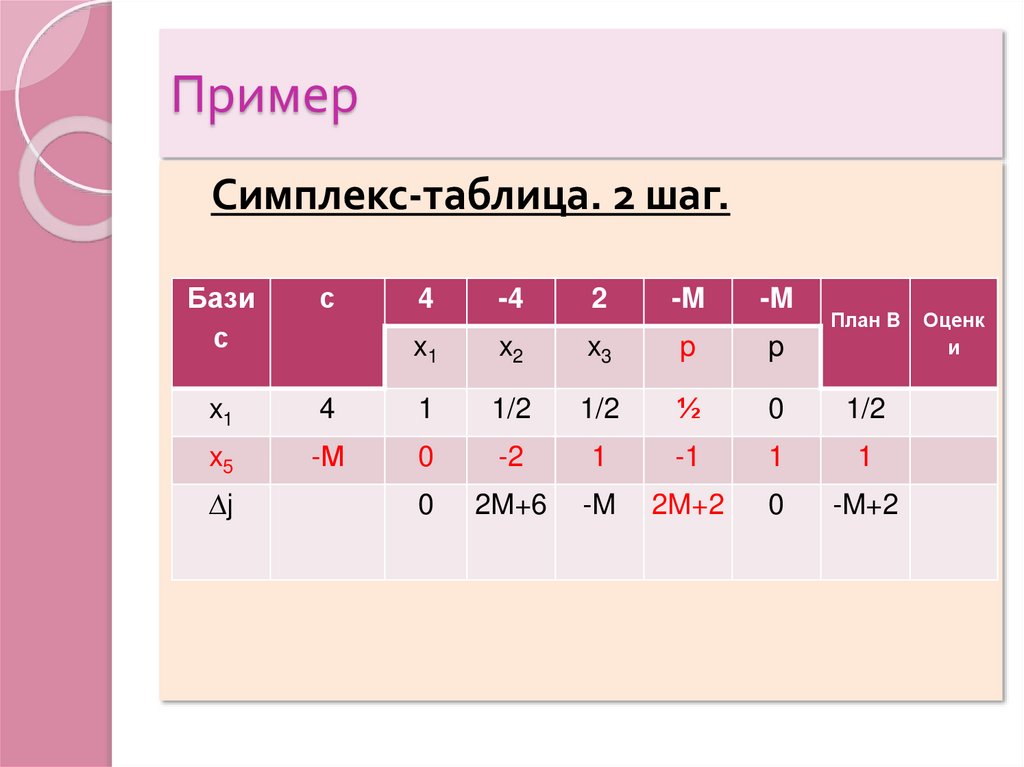
19. Пример

Симплекс-таблица. 2 шаг.
Бази
с
с
x1
x5
∆j
4
-4
2
-M
-M
x1
x2
x3
p
p
4
1
1/2
1/2
½
0
1/2
-М
0
-2
1
-1
1
1
0
2M+6
-M
2M+2
0
-M+2
План B
Оценк
и

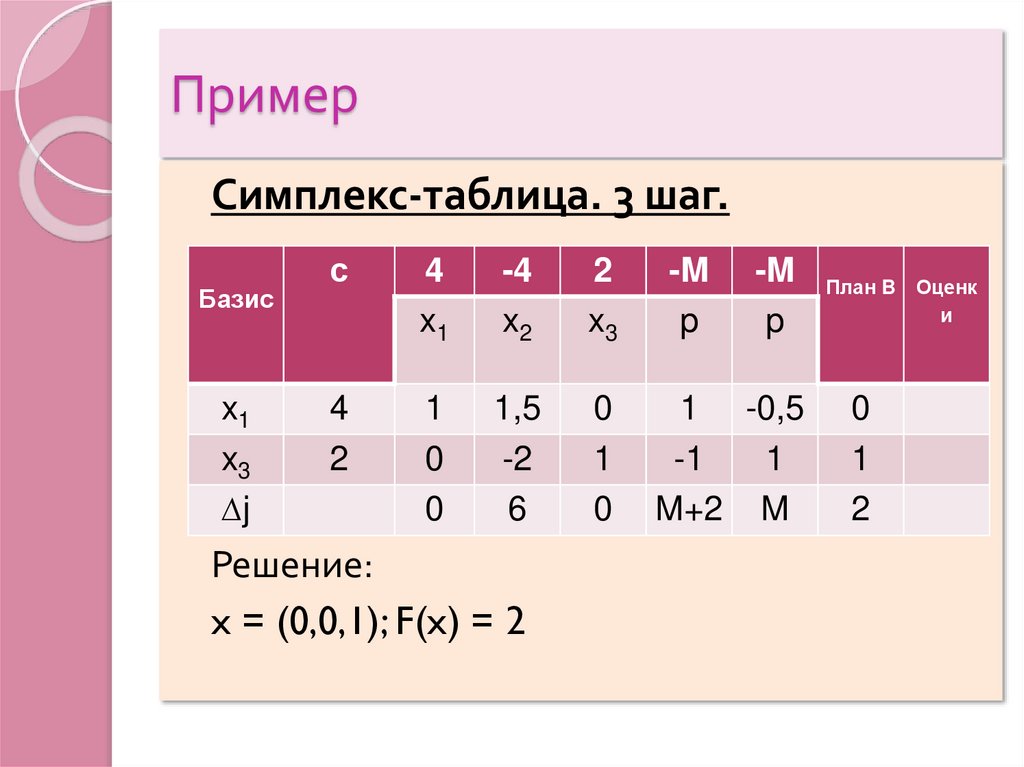
20. Пример

Симплекс-таблица. 3 шаг.
Базис
x1
x3
∆j
с
4
x1
-4
x2
2
x3
-M
p
4
2
1
0
0
1,5
-2
6
0
1
0
1 -0,5
-1
1
M+2 M
Решение:
x = (0,0,1); F(x) = 2
-M
p
План B Оценк
и
0
1
2