Similar presentations:
Интегралы. Первообразная функция. Неопределенный интеграл
1. интегралы
2. Таблица основных неопределенных интегралов
3.
Пример.воспользуемся формулой
1
2
xdx x dx
x
3
2
x
n
x
dx
C
,
n
1
n 1
2 3
3 C
x C
3
2
n 1
4.
Пример.воспользуемся формулой
1
13
n 1
dx
x
dx
x
3x
n
x
dx
C
,
n
1
n 1
13 1
2
3
x
x
33 2
1
C
x C
3 1
2/3 2
5.
Пример.воспользуемся формулой
dx
x 2 9 dx 1 arctg x C
a2 x2 a
a
dx
1
x
arctg
C
2
3
3
9 x
6.
Пример.10
2
10
5 x 3x 4 x x 6 dx
10
2
10
5 xdx 3 x dx 4 x dx dx 6dx
x
1
1
2
10
5 x dx 3 x dx 4 x dx 10 dx 6 dx
x
2
3
11
x
x
x
5 3 4
10ln x 6 x C
2
3
11
5 2
4 11
3
x x x 10ln x 6 x C
2
11
7.
Пример.1
2
x
x 2 sin x x dx
1
x dx 2 dx sin xdx dx
x
3
x
x
2
cos x ln x C
3 ln 2
2
x
8.
Пример.4
sin x
sin
x
d
sin
x
C
,
4
2
ln x
ln
x
d
ln
x
C
2
4
t
3
t
dt
C
4
3
9.
Пример.2sin x 6 3x dx 2sin xdx 6dx 3x dx
2
2
2 sin xdx 6 dx 3 x dx
2
3
x
3
2cos x 6 x 3 C 2cos x 6 x x C .
3
10.
Замечание. Задача всех остальных методов – привестиинтеграл
к
виду,
позволяющему
выполнить
непосредственное интегрирование.
При сведении данного интеграла к табличному часто
используются следующие преобразования дифференциала
(операция «внесение под знак дифференциала»):
11.
Пример.x 5 xdx x 5 x x 5 '
x 5 x d x 5 1
x 5 d x 5
2 x
2
d x 5
2
10
2
10
2
2
2
10
2
2
1 x 5
2
11
2
C x 5 C.
11
11
2
22
10
2
12.
sinUdU
cos
U
C
Пример.
x sin x dx x sin x x '
x sin x d x 1
sin x d x
2 x
2
2
2
d x
2
2
2
2
2
1
2
cos x C.
2
2
13.
Пример.d x 5
2
x
x
dx
x2 5
x2 5 x2 5 '
x d x 5
2
1
1
2
2 x 5
x 5 2 x
d
x
5
1
1
ln x 5 C.
2 x 5 2
2
2
2
2
d x 5
2
14.
Пример.d 1 x
1
xdx
1
x
dx
1
x
1 x '
1
2
1
2
1
d 1 x
2
1 x
1 x d 1 x
1
1
2
1 x
2 3
C
x C
3
2
3
2
3
15. Метод подстановки или замены переменной
Данный метод заключается во введении новойпеременной интегрирования. При этом заданный интеграл
приводится к новому интегралу, табличному или
сводящемуся к нему.
f x dx
Пусть требуется вычислить
Сделаем подстановку x=φ(t), где φ(t) – функция,
имеющая непрерывную производную.
Тогда dx=φ’(t)dt. Следовательно, формула замены
переменной в неопределенном интеграле будет иметь вид:
f
x
dx
f
t
t
dt
16.
Замечание. После нахождения интеграла следует перейтиот новой переменной интегрирования t назад к x.
Пример.
x
t
,
x
4
t
,
x
4
e dx 4
dx 4t ' dt 4dt
x
4
e 4dt 4 e dt 4e C 4e C.
t
t
t
17.
Пример.t x 3, x t 2 3,
x x 3dx dx 2tdt
t 3 t 2tdt 2 t 3t
2
5
3
t
t
2
2 6 C
5
3
5
4
2
dt
x 3 2 x 3 C.
5
3
18.
Пример.t x
cos x
x dx dt
x ' dx dt 2 x dx
1
dx 2 x dt
cos t
2 x dt 2 cos tdt 2sin t C
x
2sin x C.
19. Метод интегрирования по частям
udvuv
vdu
20.
Пример.u u x x,
du dx
dv
e
dx
,
v
e
dx
e
x
e
dx
e
dx
dv
e
dx
xx
xx
x
udv
uv
vdu
udv
uv
vdu
x e e dx xe e C
x
x
x
x
x
21.
Пример.dx
u ln x, du ln x ' dx
x
ln
xdx
dv
dx
dv dx,
v dx x
udv
uv
vdu
udv uv vdu
dx
x ln x x x ln x dx
x
x ln x x C
22.
Рассмотрим случаи применения метода интегрирования почастям.
Pn ( x)
e kx dx
Pn ( x)
cos xdx
Pn ( x)
sin xdx
ln x
Pn ( x)dx
arcsin x
Pn ( x)dx
arccos x
Pn ( x)dx
arctgx
Pn ( x)dx
arcctgx
Pn ( x)dx
Формула интегрирования по
частям применяется два раза,
при этом за U выбирается одна
и та же функция
23.
Пример.u x,
du x ' dx du dx
1
x sin 2 xdx dv sin 2 xdx, v sin 2 xdx 2 cos 2 x
udv uv vdu
1
1
1
1
x cos 2 x cos 2 x dx x cos 2 x cos 2 xdx
2
2
2
2
d 2x
1
1
1
1
x cos 2 x cos 2 x
C x cos 2 x sin 2 x C
2
2
2
2
4
24.
dx2t
1 t
2dt
x
4sin x 3cos x 3 t tg 2 ; sin x 1 t 2 ; cos x 1 t 2 ; dx 1 t 2
2
2dt
2
2 1 t dt
2
1
t
2
2
2
2
1 t
1 t 8t 3 3t 3 3t
2t
4
3
3
2
2
1 t 1 t
2dt
8t 6
dt
4t 3
1
ln 4tg 2x 3 C.
4
1 d 4t 3
4 4t 3
1
ln 4t 3 C
4
25.
x 2x 4 x 2 dx
Пример .
Сумма простых дробей примет вид:
x 2
A B Cx D
2 2
2
2
x
x x 1 x
x 1
26.
Найдём числа A,B,C,D методом неопределённыхкоэффициентов: приведём слагаемые в правой части
равенства (10) к общему знаменателю, раскроем скобки,
сгруппируем слагаемые с одинаковыми степенями :
x 2
x
2
x 2
x 1
2
x x 1
2
2
x 2 1
A
x
2
x x 2 1
B
x
x2
Cx D
x 1
2
A x 1 Bx x 1 Cx D x
2
2
x x 1
2
2
x 2
B C x A D x Bx A
2 2
2 2
x x 1
x x 1
3
2
2
27.
Слева и справа от знака равенства находятся дробнорациональных функции с равными знаменателями.Следовательно, их числители должны быть равны
x 2 B C x A D x Bx A
3
2
Для
нахождения
чисел
A,B,C,D
приравняем
коэффициенты многочленов при одинаковых степенях х.
x : B C 0,
3
2
x :
A D 0,
1
x :
B 1,
0
A 2;
x :
A 2,
A 2,
B 1,
B 1,
C
B
,
C
1
,
D A;
D 2,
28.
A 2,B 1,
C
1,
D 2,
Подставим найденные
коэффициенты в равенство
x 2
2 1 x 2
2 2
2
2
x x 1
x x 1 x
И вычислим интеграл от полученной функции
29.
x 2x 4 x 2 dx
2dx dx
x 2
2 1 x 2
x 2 x x 2 1 dx x 2 x x 2 1 dx
2
x
2dx
ln x 2
dx 2
x
x 1
x 1
2
x d x 1
dx
ln x 2
2 2
x
x 1 2x
x 1
2
1
2
ln x ln x 1 2arctg x C.
x
2
2
30.
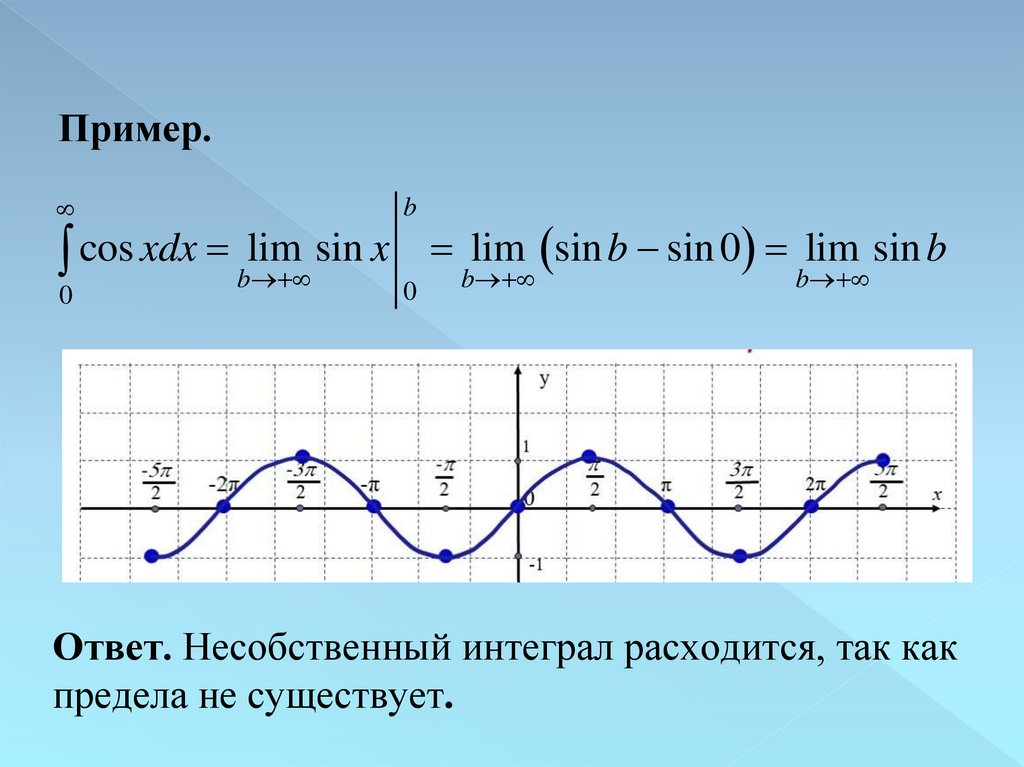
Пример.b
0
0
sin x
cos xdx blim
lim sin b sin 0 lim sin b
b
b
Ответ. Несобственный интеграл расходится, так как
предела не существует.
31.
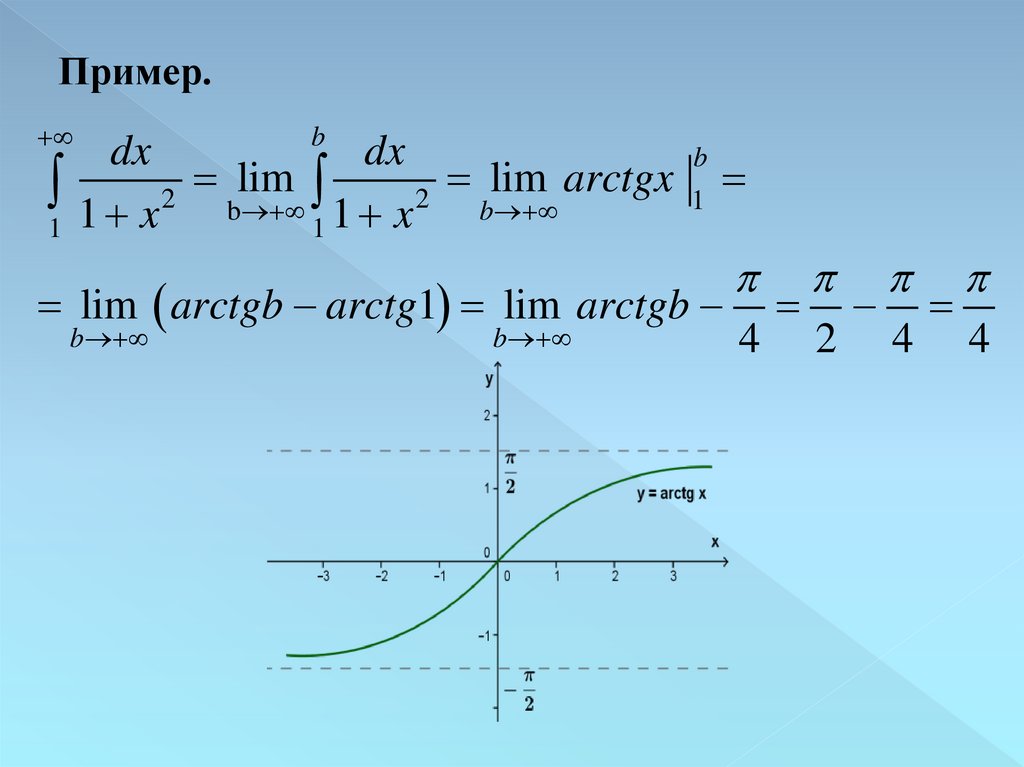
Пример.b
dx
dx
b
lim
arctgx
1 x 2 blim
1
1 x 2
b
1
1
lim arctgb arctg1 lim arctgb
b
b
4
2
4
4
32.
Пример.dx
dx
1
2
lim
x
dx
lim
x 2 blim
x 2
b
b x
1
1
1
1
b
b
b
1 1
lim 0 1 1
b b
1
Ответ. Несобственный интеграл сходится и равен 1.
33.
Пример.1
1
1
dx
dx
lim
lim
ln
x
x a x a
a
a
lim ln 1 ln a 0
a
Ответ. Несобственный интеграл расходится.





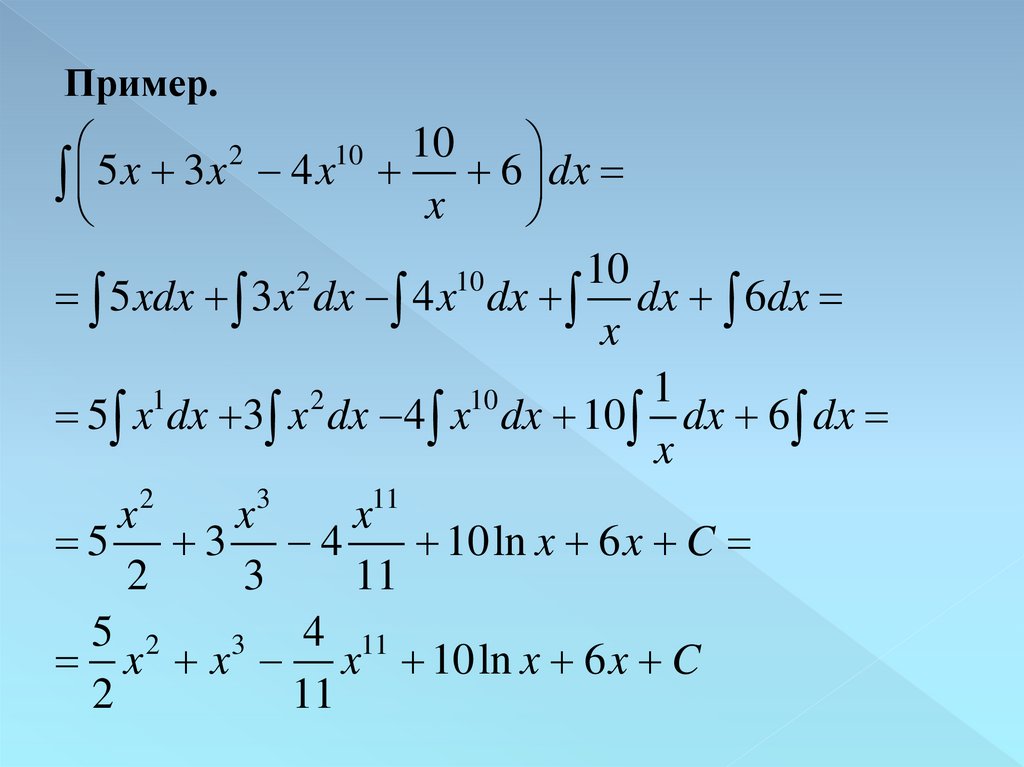
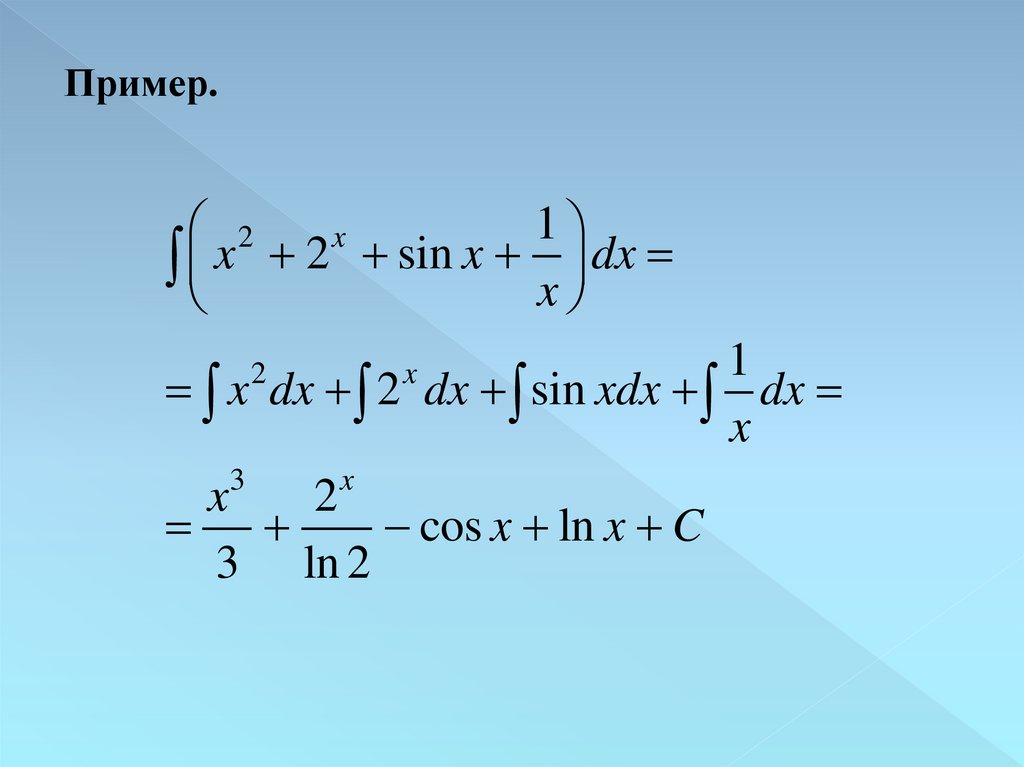
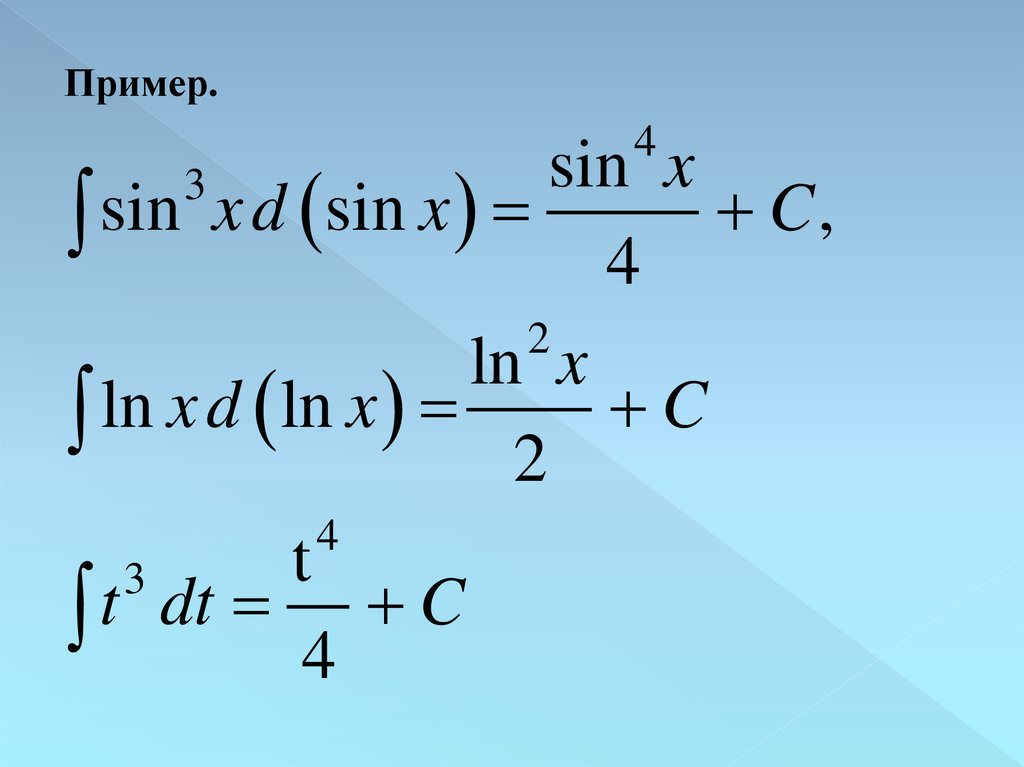
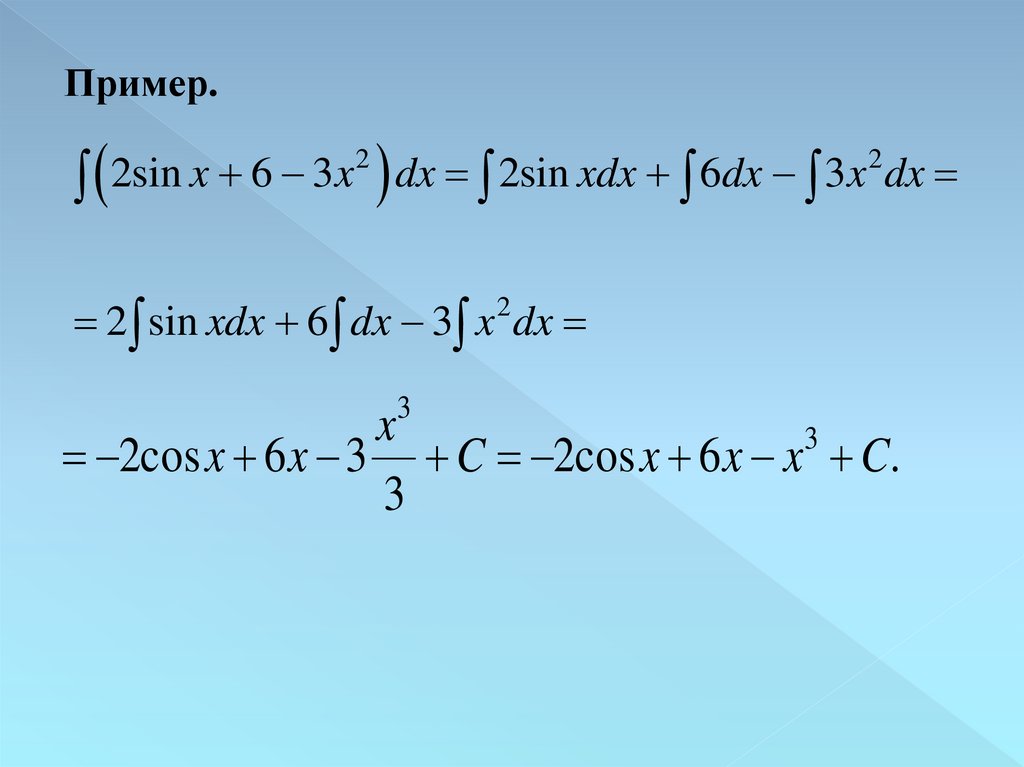

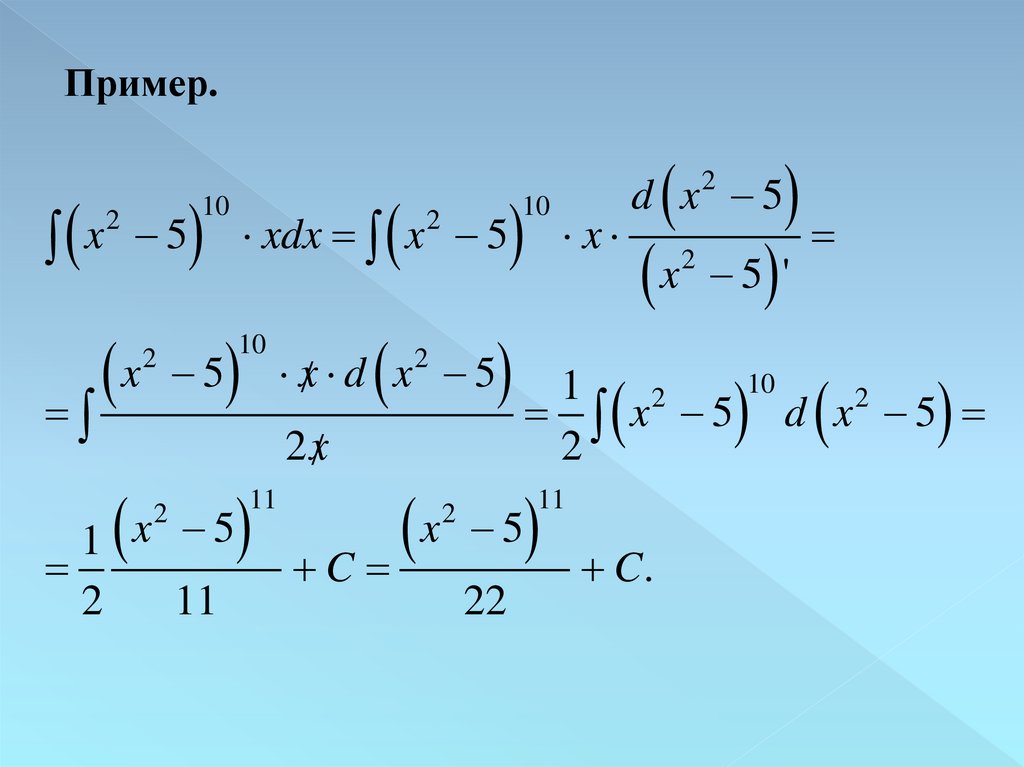
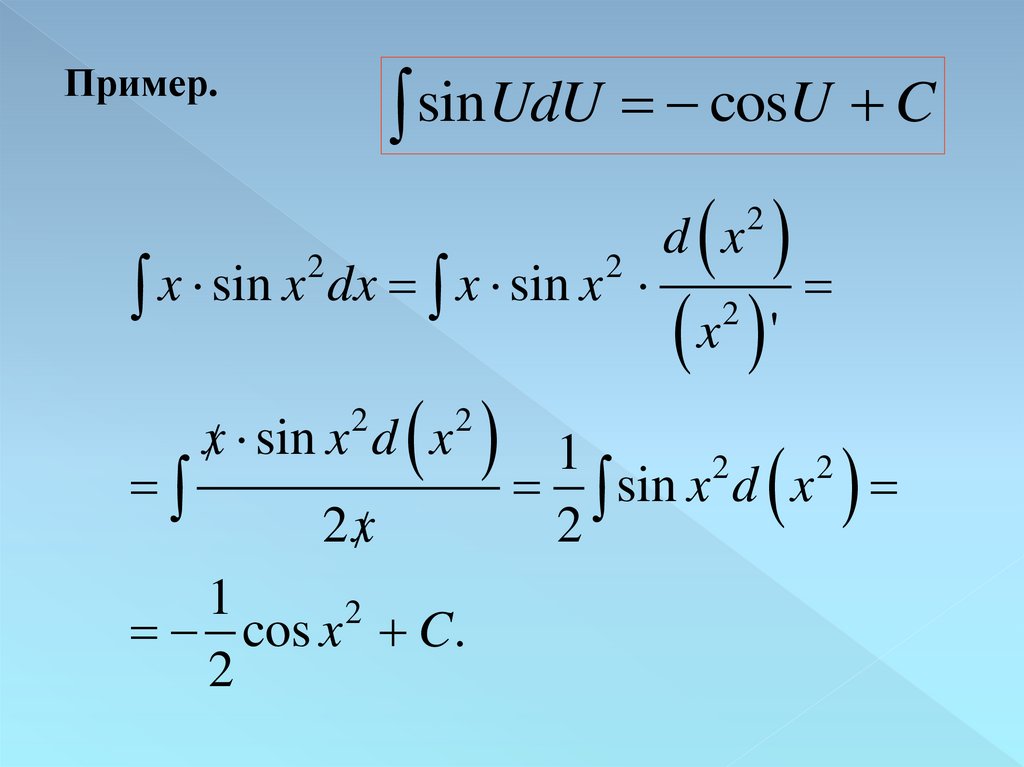
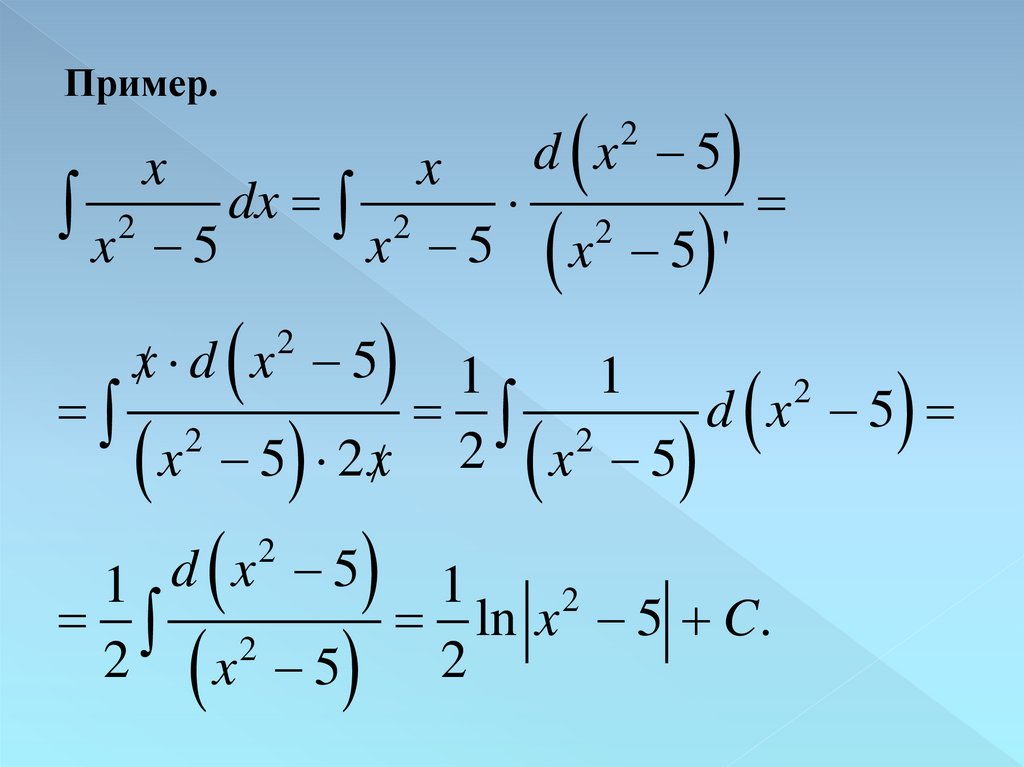
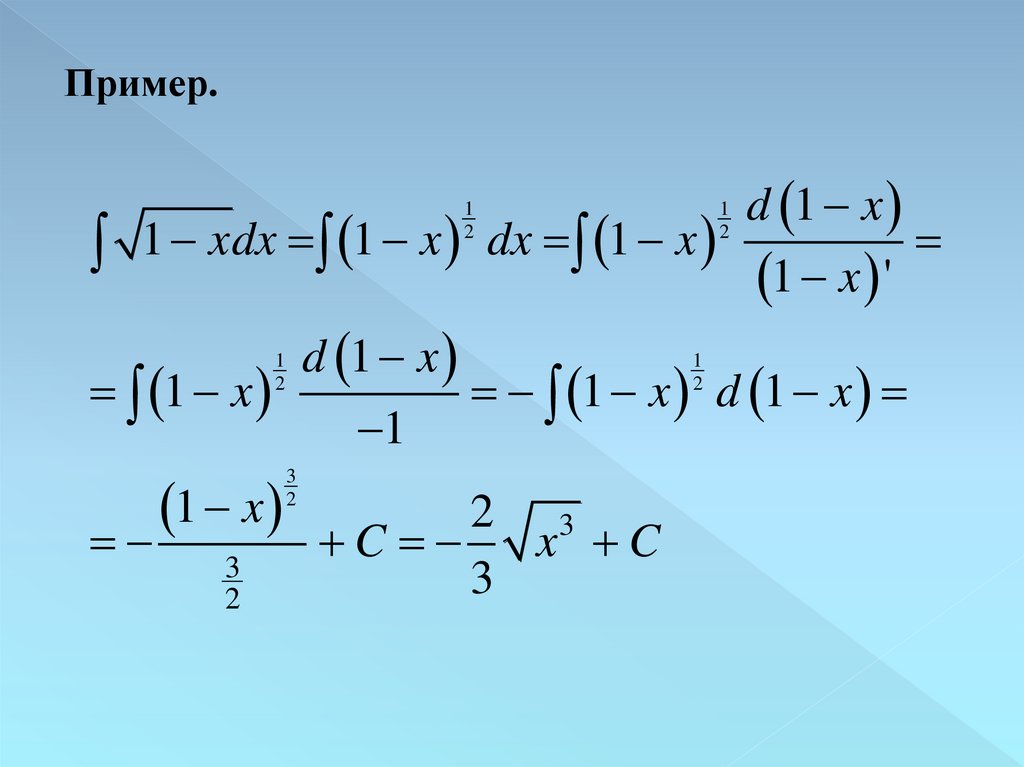


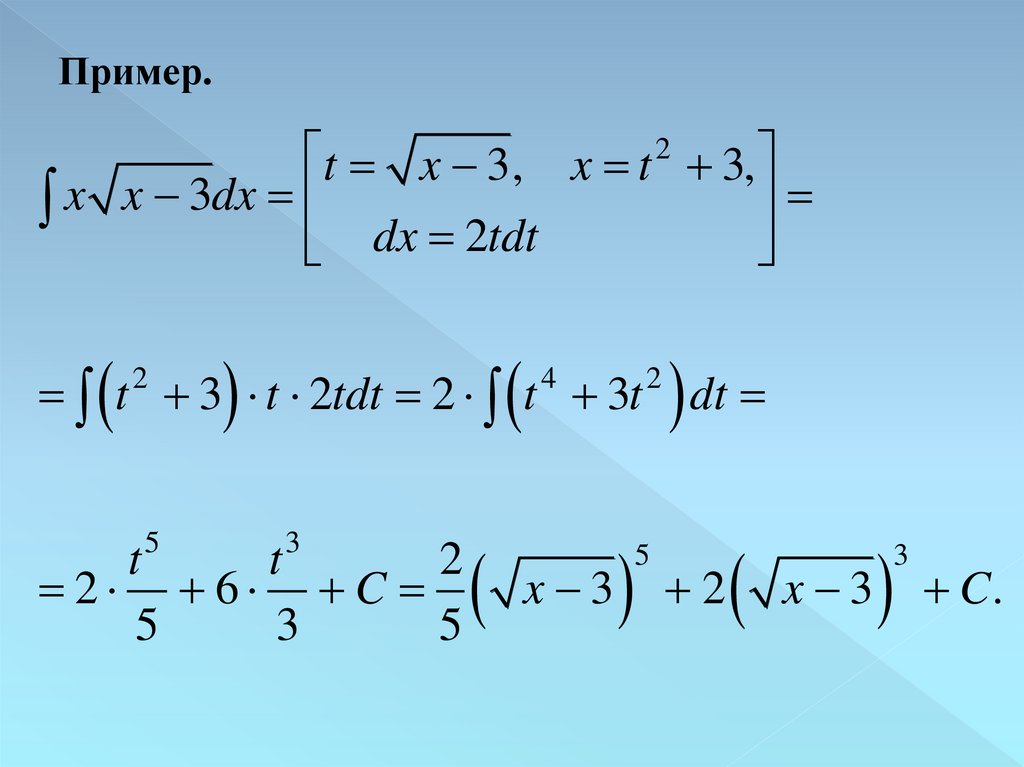
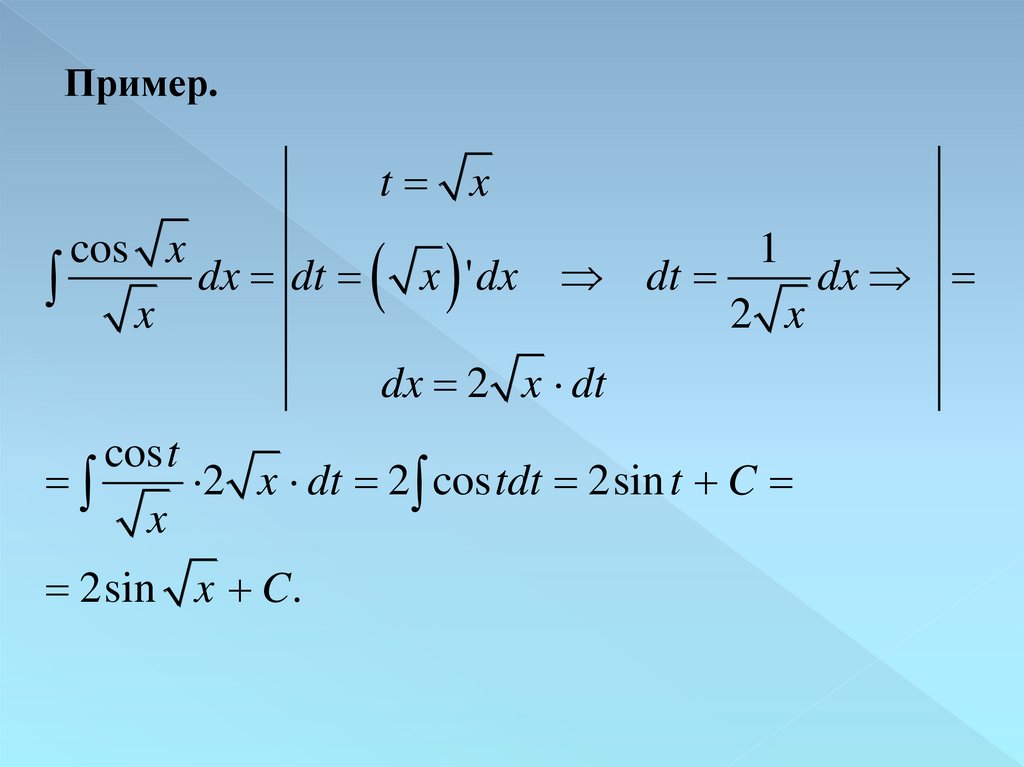

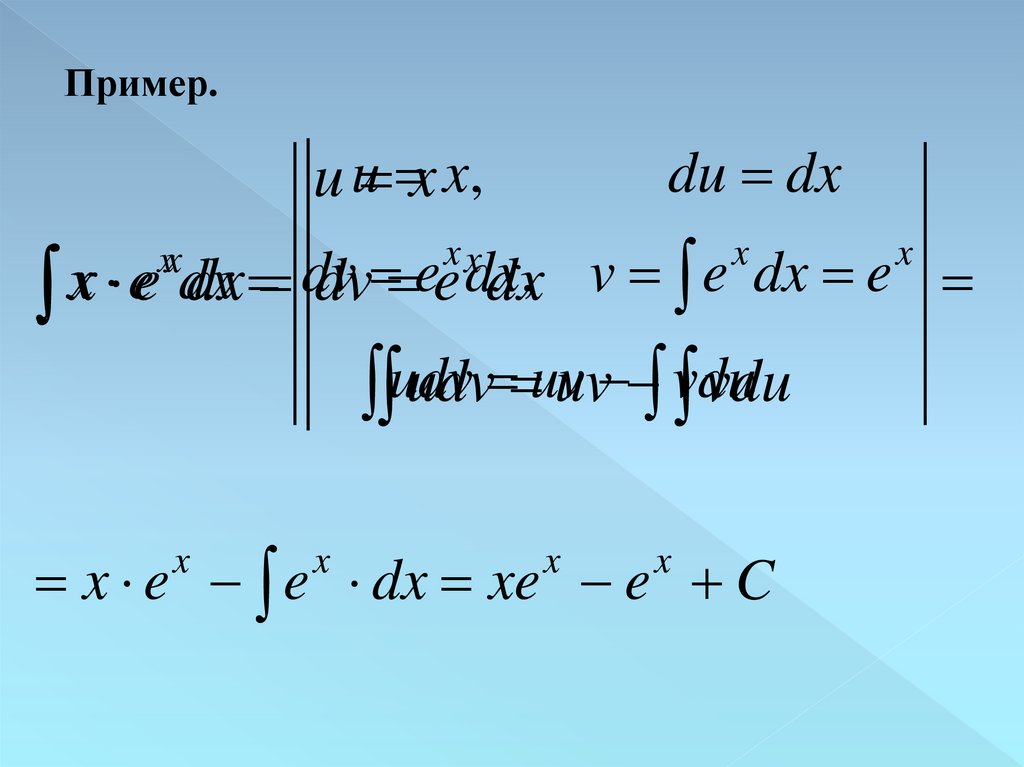
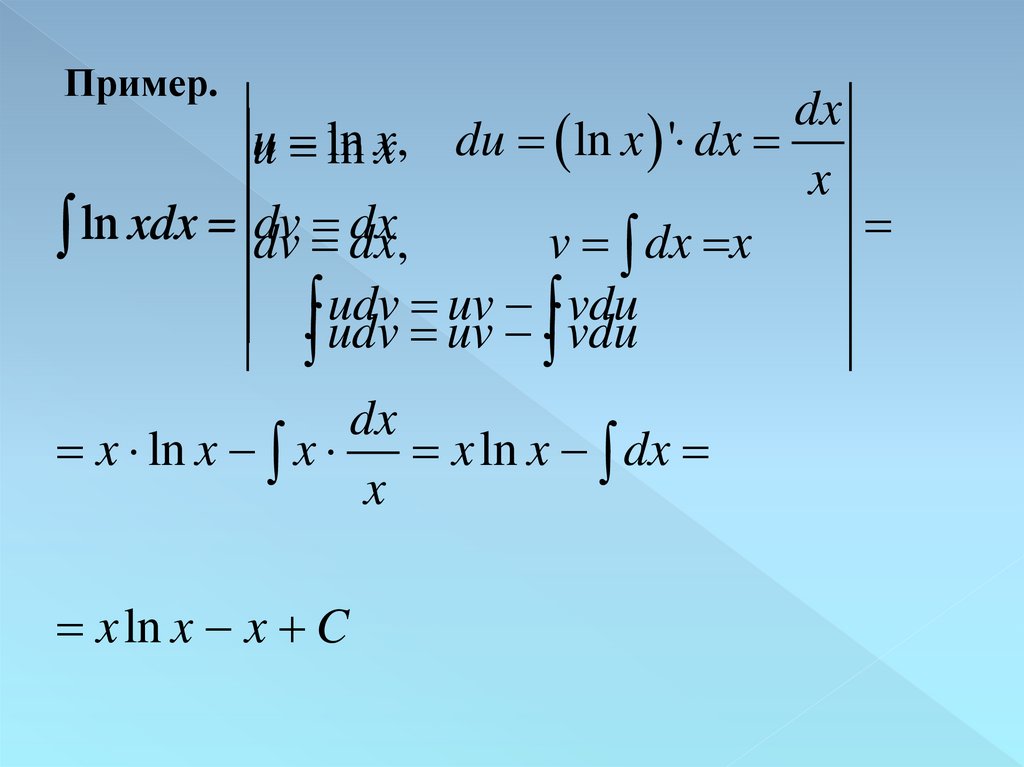

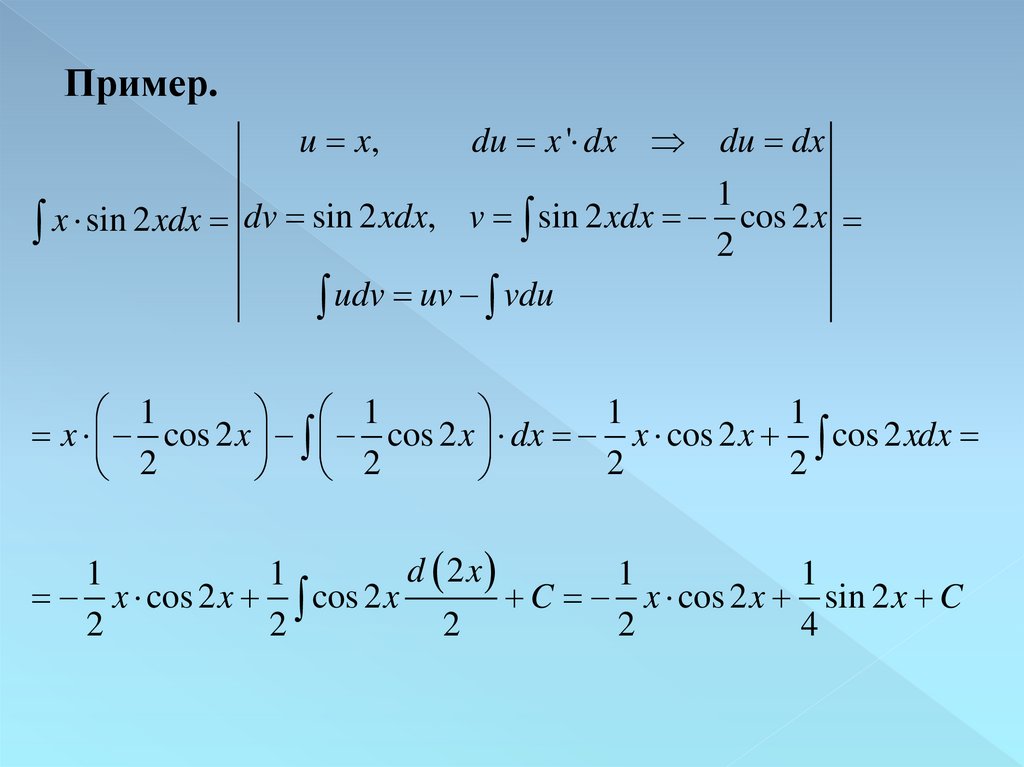
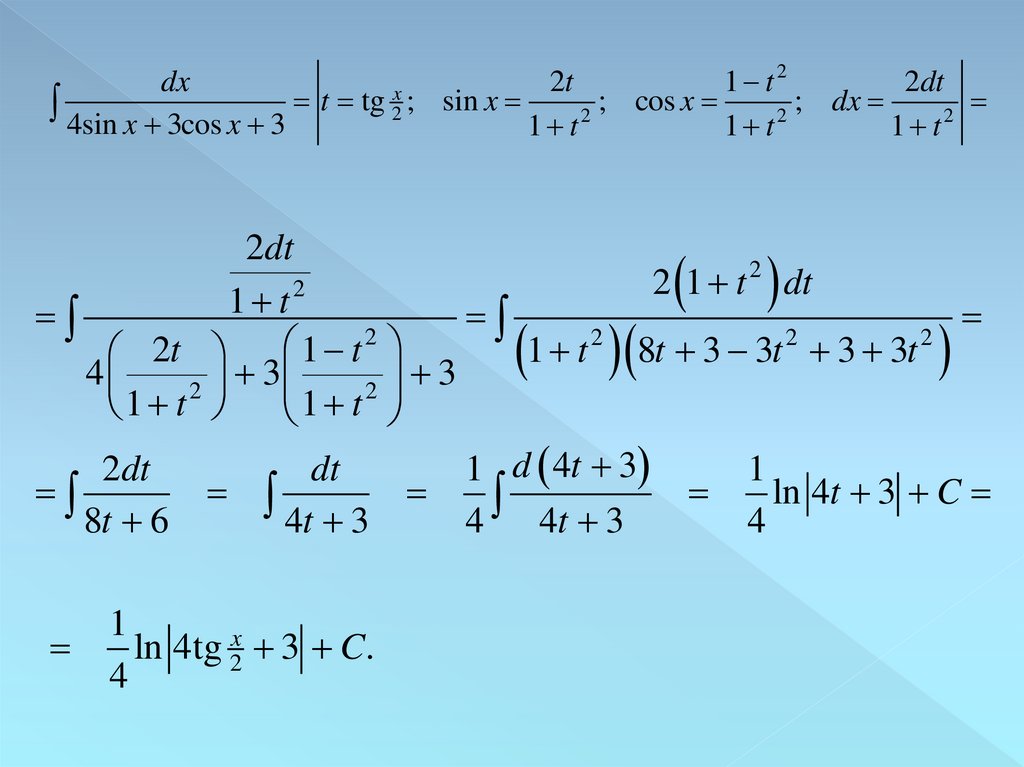




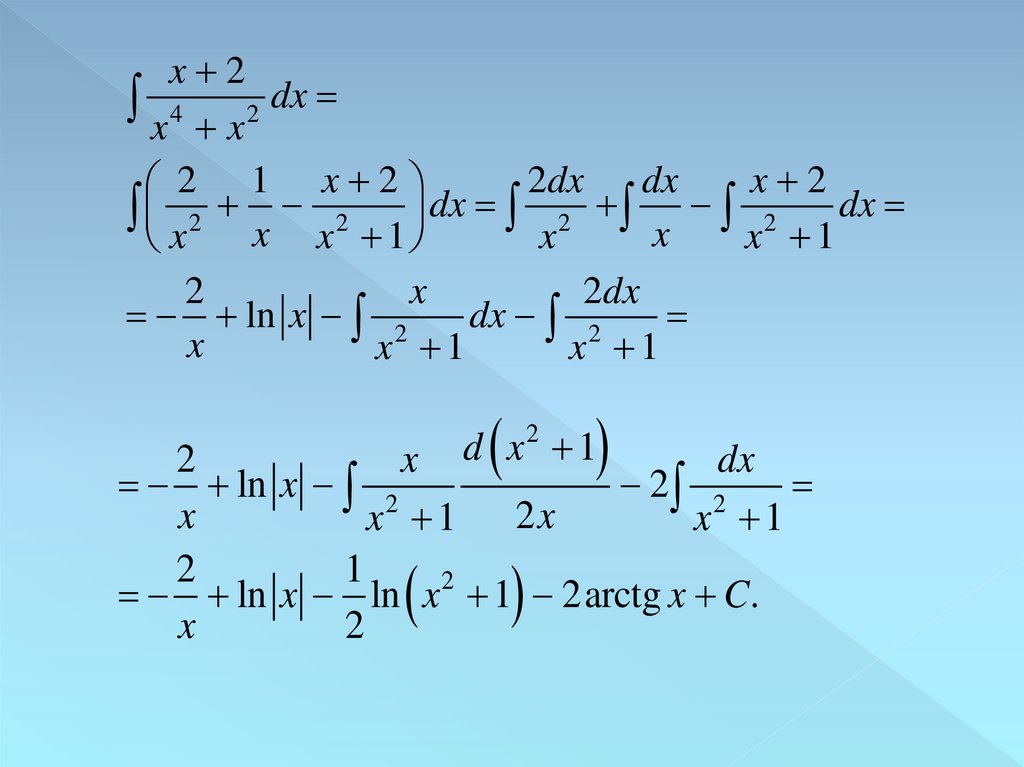



 mathematics
mathematics








