Методы оптимизации. Линейное программирование

1.

МЕТОДЫ ОПТИМИЗАЦИИ

2.

ЛИНЕЙНОЕ
ПРОГРАММИРОВАНИЕ
2

3.

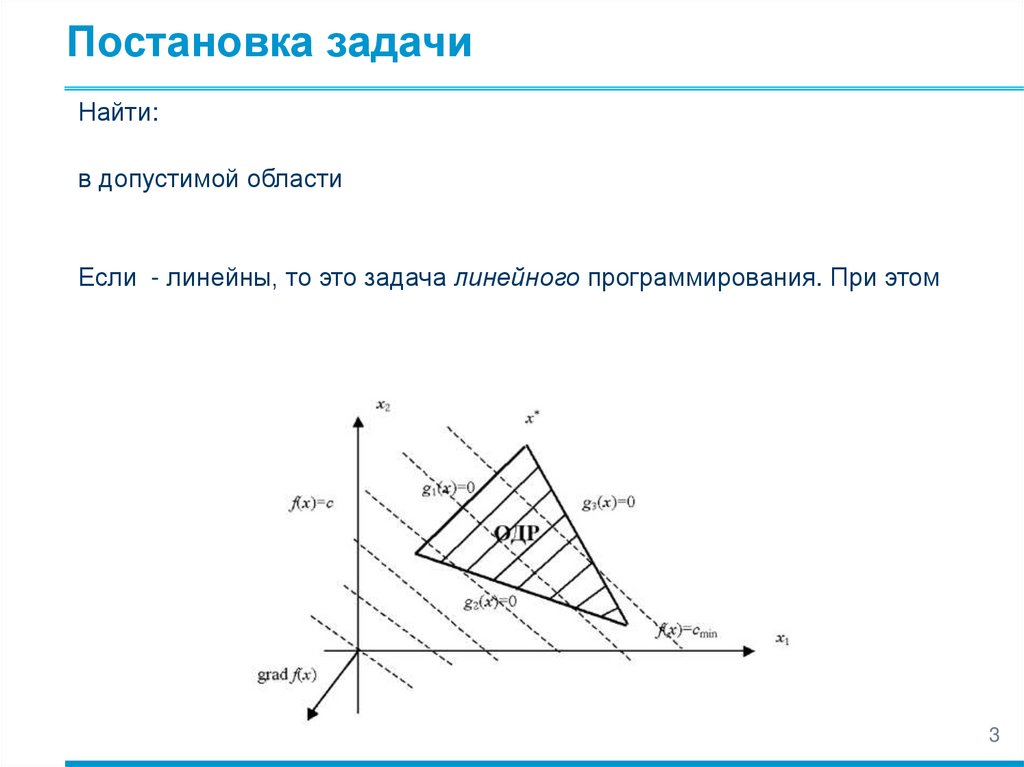
Постановка задачи
Найти:
в допустимой области
Если - линейны, то это задача линейного программирования. При этом
3

4.

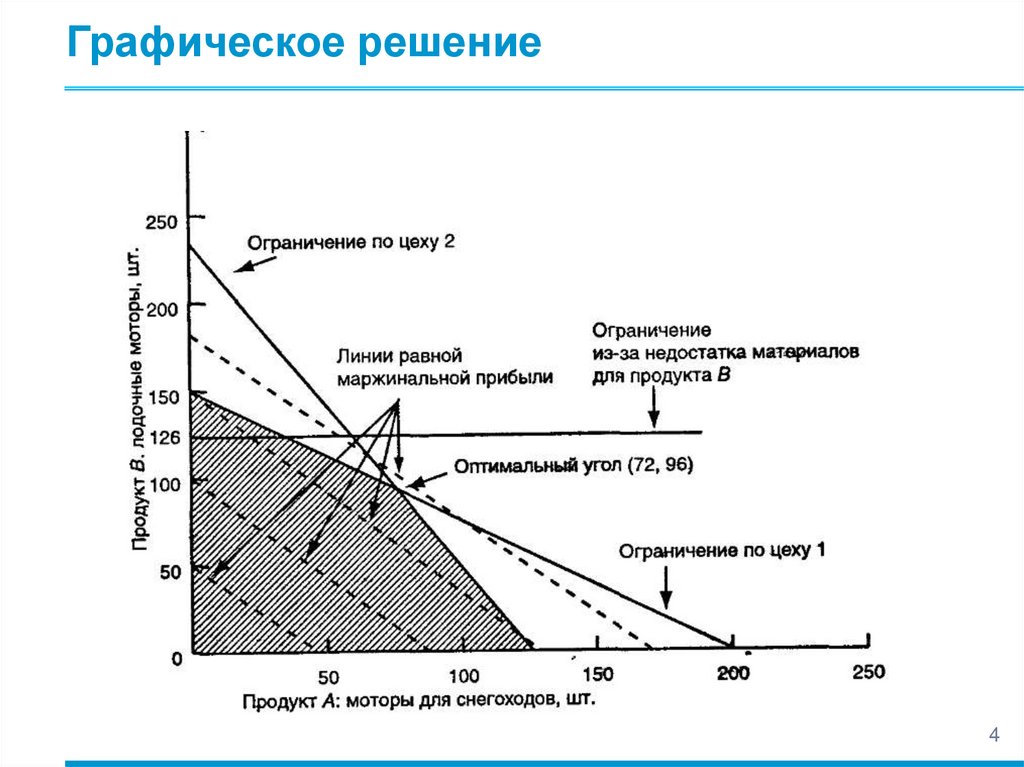
Графическое решение
4

5.

Формы представления задачи ЛП
Общая форма
Ограничения представлены в виде равенств и неравенств
Стандартная форма
Неравенства превращены в эквивалентные равенства с помощью введения
фиктивных переменных:
Эквивалентное равенство:
При этом: общее число переменных, общее число равенств системы.
5

6.

Формы представления задачи ЛП
Каноническая форма
Целевая функция:
- базисные переменные, оставшиеся - свободные переменные.
Базисное решение (БР):
Допустимое базисное решение (ДБР):
Метод Жордана – Гаусса, Теорема Кронекера – Капелли, ранг матрицы,
базисный минор,
6

7.

Симплекс-метод
Приращение целевой функции
Поиск ведется по смежным ДБР.
Смежные ДБР отличаются одной базисной переменной.
ДБР:
Приращение по :
Положим ,
Отсюда:
Если все то решение – оптимальное.
Задание: описать алгоритм!
7

8.

Симплекс-метод
Поиск ДБР
Метод замены переменных
8

9.

Симплекс-метод
Основные этапы
Шаг 1. Привести задачу линейного программирования к канонической
форме с n неизвестными.
Шаг 2. В системе из m уравнений выбрать m базисных переменных,
остальные n – m считать свободными. Выразить базисные переменные
через свободные и найти соответствующее базисное решение. Если
найденное базисное решение окажется допустимым, перейти к
допустимому базисному решению.
Шаг 3. Выразить ЦФ через базисные переменные ДБР. Если все
приращения ЦФ по свободным переменным не отрицательны, то
полученное базисное решение является оптимальным. STOP.
Шаг 4. Из свободных переменных выбирают ту, которой соответствует
наибольшее (по модулю) отрицательное приращение ЦФ, и переводят её в
базисные. Переход к шагу 2.
9

10.

Симплекс-метод
Правило замены базисной и свободной переменных
Рассмотрим матрицу коэффициентов и свободных членов системы
линейных уравнений-ограничений, построенной для данного ДБР.
Замена базисной и свободной переменной заключается в выборе
направляющего столбца и направляющей строки и замене
соответствующих им переменных.
Выбор направляющего столбца :
Выбор направляющей строки :
10

11.

Симплекс-метод
Симплексные таблицы
11

12.

Симплекс-метод
Симплексные таблицы
12

13.

Кейс 2
Источник:
Смирнов А.П. Методы оптимизации: учеб. пособие. – М.: МИСиС, 2003. –
131 с.
Пусть требуется спланировать на один месяц работу цеха, в котором
имеются два типа станков. Цех должен производить два вида изделий,
причем каждый тип станка может производить оба вида изделия, но с
разной производительностью (количество изделий в месяц). Известна
себестоимость изделий каждого вида.
Имеются ограничения, состоящие в том, что нельзя произвести изделий
каждого вида меньше, чем задано, а также необходимо, чтобы все станки
были заняты. При этих условиях нужно получить минимальную себестоимость произведенного товара.
13

14.

Кейс 2
Введем систему неизвестных.
Обозначим количество станков первого типа, предназначенных для
изготовления изделий первого и второго видов как
Производительность таких станков 3 и 6 тыс. штук в месяц соответственно.
Обозначим количество станков второго типа, предназначенных для
изготовления изделий первого и второго видов как
Производительность таких станков 10 и 5 тыс. штук в месяц
соответственно.
Количество станков первого типа равно 20, второго типа - 40. Задание на
производство: 200 тысяч изделий первого вида и 100 тысяч изделий второго
вида.
Себестоимость тысячи изделий первого вида 2 у.е., второго вида - 5 у.е.
14