Линейное программирование. Графический метод

1.

Линейное
программирование
Графический метод

2.

Литература
• Таирова Е.В. Линейное программирование: учебное пособие /Е.В
Таирова. – Иркутск: ИрГУПС, 2007. – 75 с.
• https://sdo2.irgups.ru/pluginfile.php/22444/mod_resource/content/
1/Линейное%20прог%20Таирова.pdf
• Аргучинцев А.В. Введение в оптимизацию: учеб. пособие / А.В.
Аргучинцев, А.И.Беников. –Иркутск : Изд-во ИГУ, 2011. –Вып. 3. –
105с.
• https://studylib.ru/doc/6226410/arguchincev-a.v.--benikov-a.i.vvedenie-v-optimizaciyu.-uche...

3.

Наш мир – лучший из миров
• Готфрид Лейбниц
• «Бог действует всегда самым совершенным и наиболее
желательным образом»[4]. Следовательно, Его выбор всегда
будет лучшим. Следовательно,
• «Вселенная, которую избрал Бог, является лучшим из всех
возможных миров»[2].

4.

Оптимизация
• Оптимизация (в математике, информатике и исследовании операций)
— это задача нахождения экстремума (минимума или максимума)
целевой функции в некоторой области конечномерного векторного
пространства, ограниченной набором линейных и/или нелинейных
равенств и/или неравенств.
• Условная и безусловная оптимизация

5.

Методы оптимизации

6.

Глобальный и локальный экстремумы

7.

Задачи оптимизации

8.

Задачи математического программирования

9.

Задача линейного программирования

10.

Краткая запись, оптимальный план

11.

Почему задачи ЛП наиболее применимы

12.

Пример задачи о производстве красок
Задача фирмы Reddy Mikks
• Небольшая фабрика фирмы Reddy Mikks изготовляет два вида красок: для внутренних (I) и наружных (E)
работ. Продукция обоих видов поступает в оптовую продажу.
• Для производства красок используются два исходных продукта-А и В. Максимально возможные суточные
запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1 т соответствующих красок и
максимально возможный запас приведены в таблице.
Исходный
продукт
Расход исходных продуктов на 1 т
краски, т
краска Е
краска I
А
В
1
2
2
1
Максимально
возможный
запас исходных
продуктов, т
6
8
• Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е
более чем на 1 т.
• Кроме этого установлено, что спрос на краску I никогда не превышает 2 т в сутки.
• Оптовые цены одной тонны красок равны:
• 3 тыс. долл. для краски Е
• 2 тыс. долл. для краски I.
• Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации
продукции был максимальным?

13.

Как построить математическую модель
• Для решения этой задачи необходимо построить математическую модель.
Процесс построения модели можно начать с ответа на следующие три
вопроса:
• 1) для определения каких величин строится модель (т.е. каковы переменные
модели);
• 2) в чем состоит цель, для достижения которой из множества всех
допустимых значений переменных выбираются оптимальные;
• 3) каким ограничениям должны удовлетворять неизвестные.
• В нашем случае фабрике необходимо спланировать объем производства
красок так, чтобы максимизировать прибыль. Поэтому переменными
являются x1– суточный объем производства краски I и x2 – суточный объем
производства краски Е.

14.

Построение математической
модели
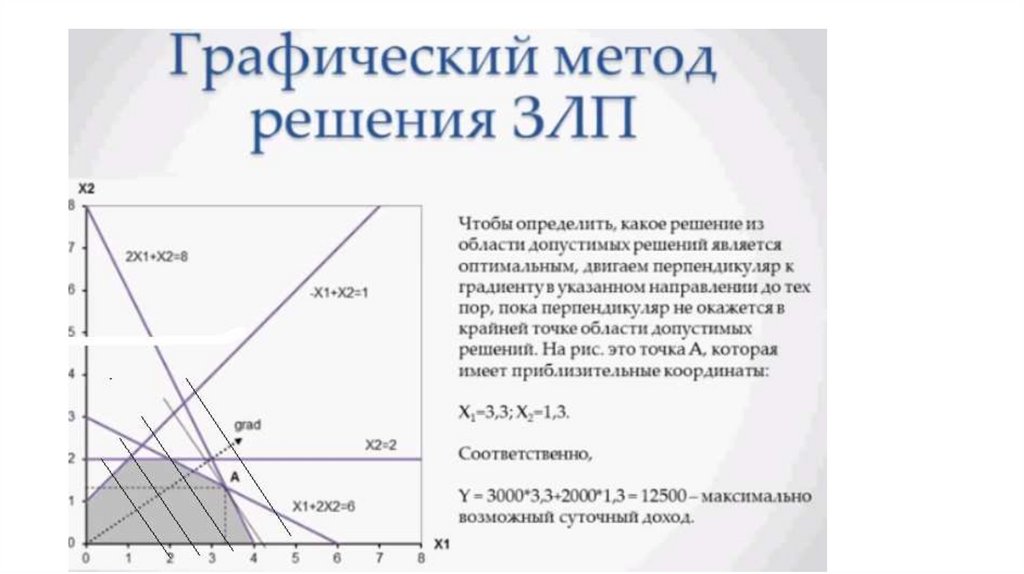
• Суммарная суточная прибыль от производства суточного
объема (x1) краски I и суточного объема (x2) краски Е
равна:
• z = 3000·x1 + 2000·x2.
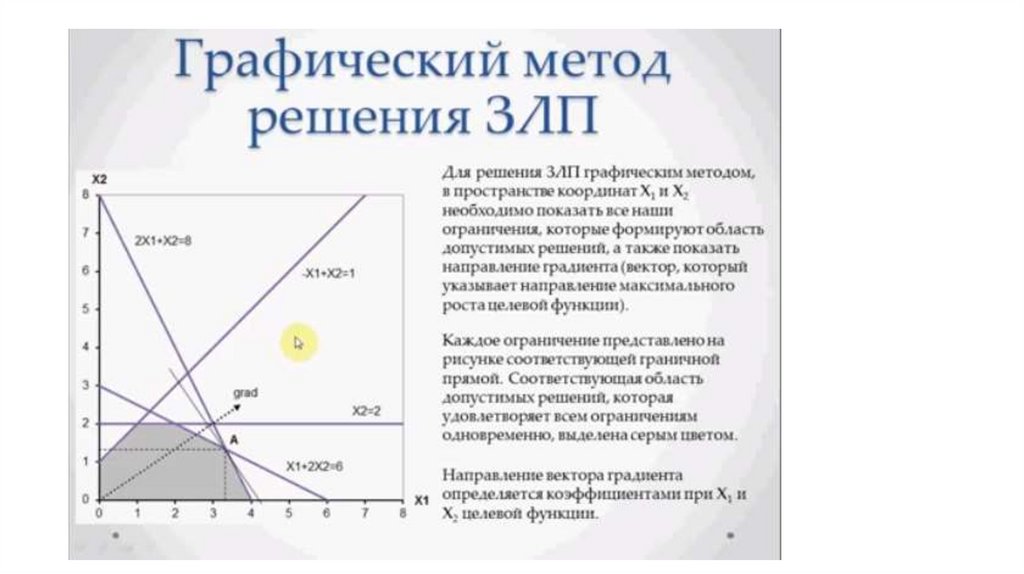
• Целью фабрики является определение среди всех
допустимых значений x1 и x2 таких, которые максимизируют
суммарную прибыль, т.е. целевую функцию z.

15.

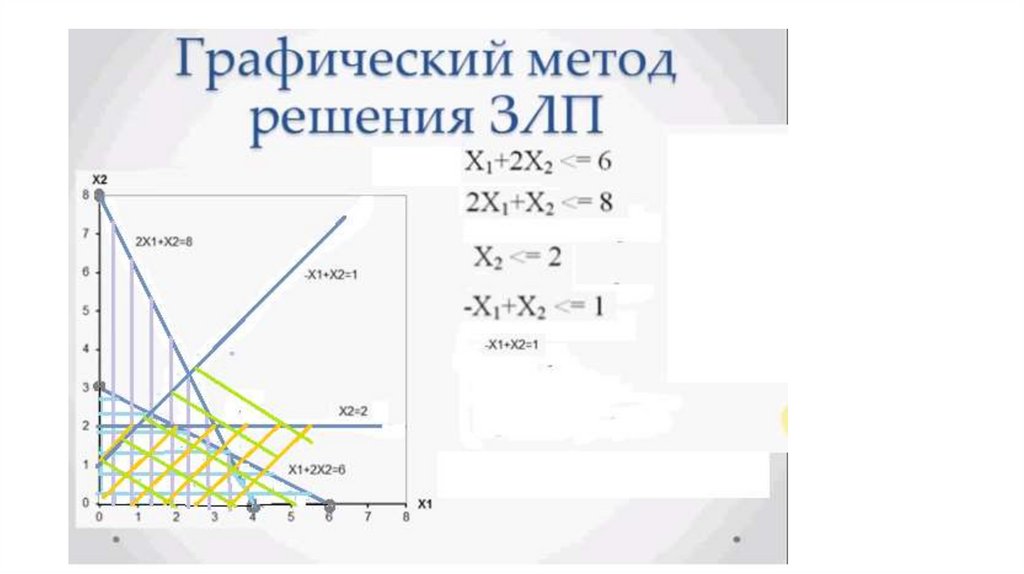
Построение математической модели
• Перейдем к ограничениям, которые налагаются на x1 и x2.
• Расход исходного продукта для производства обоих видов красок
не может превосходить максимально возможный запас данного
исходного продукта, следовательно:
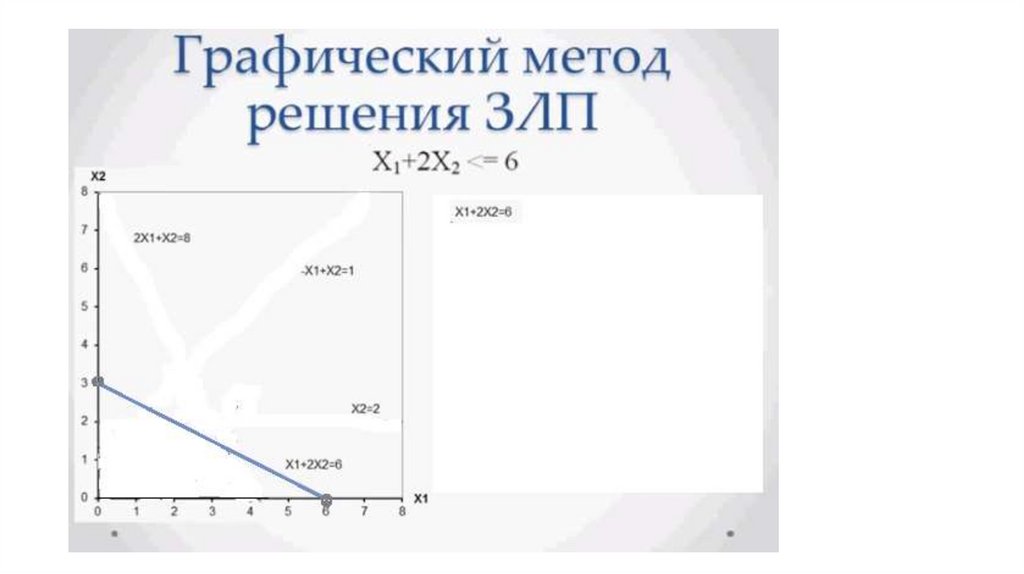
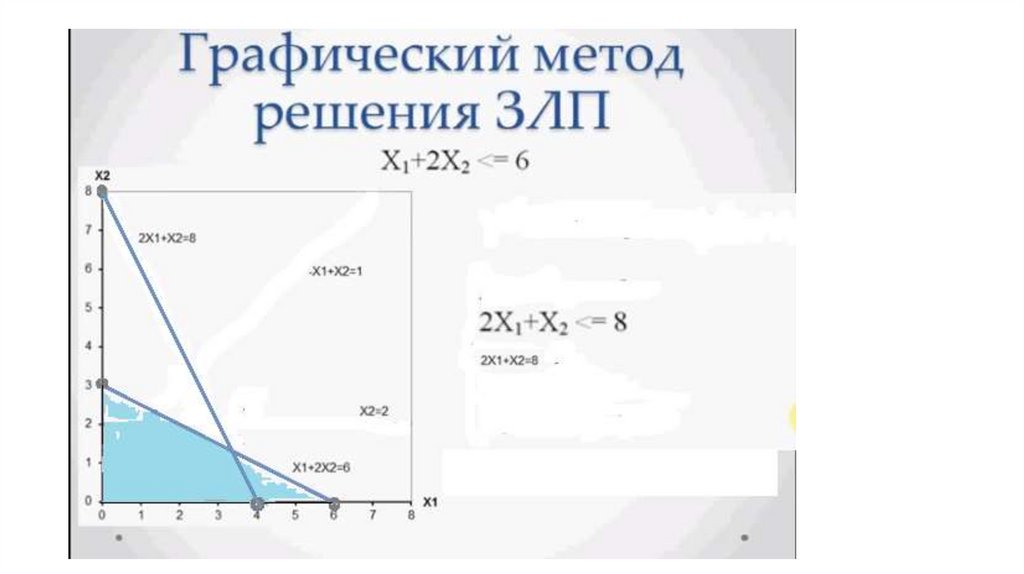
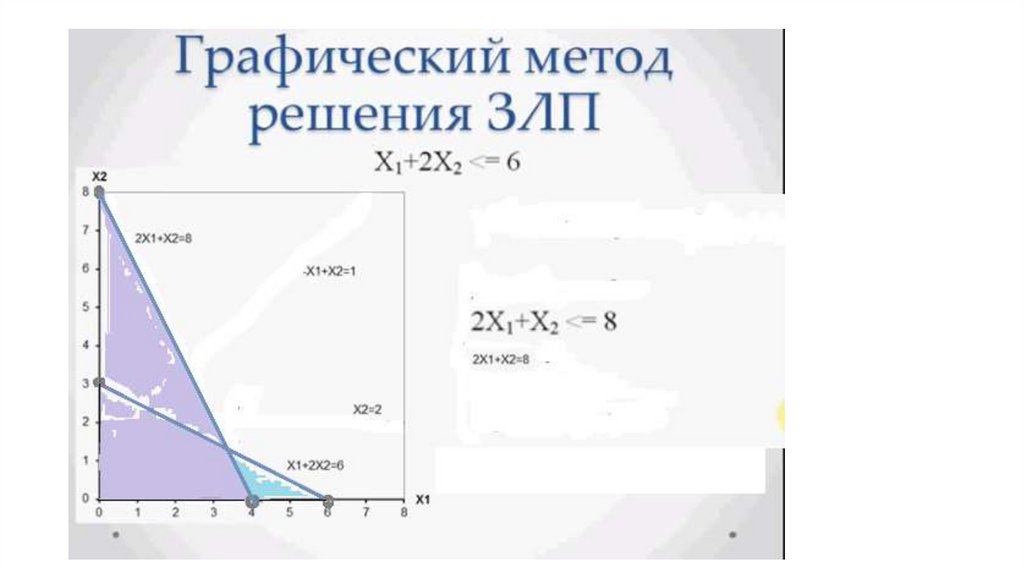
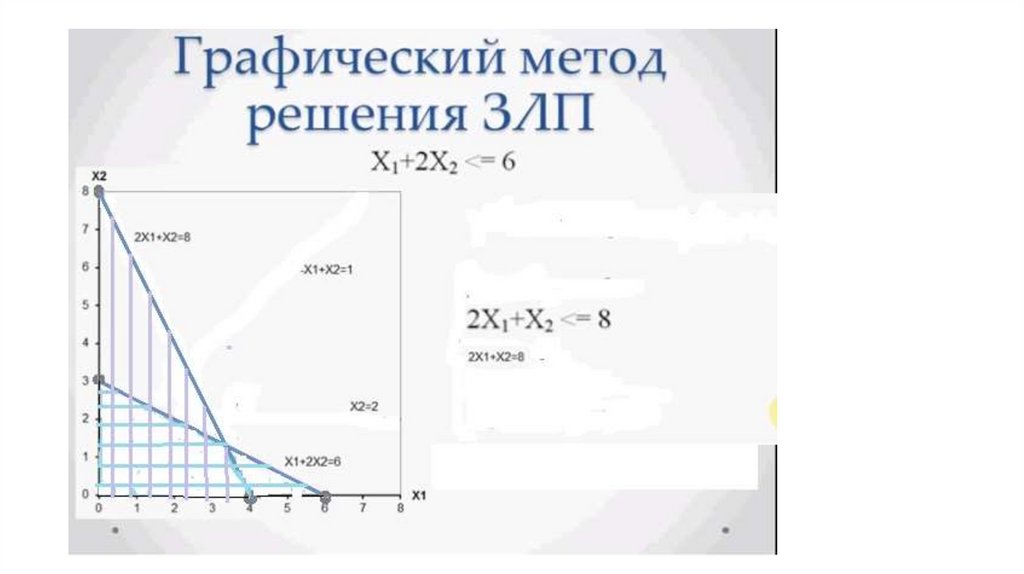
• x1 + 2·x2 ≤ 6;
• 2·x1 + x2 ≤ 8.
• Кроме того, ограничения на величину спроса на краски таковы:
• x2 – x1 ≤ 1;
• x2 ≤ 2.

16.

Математическая модель задачи о красках

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

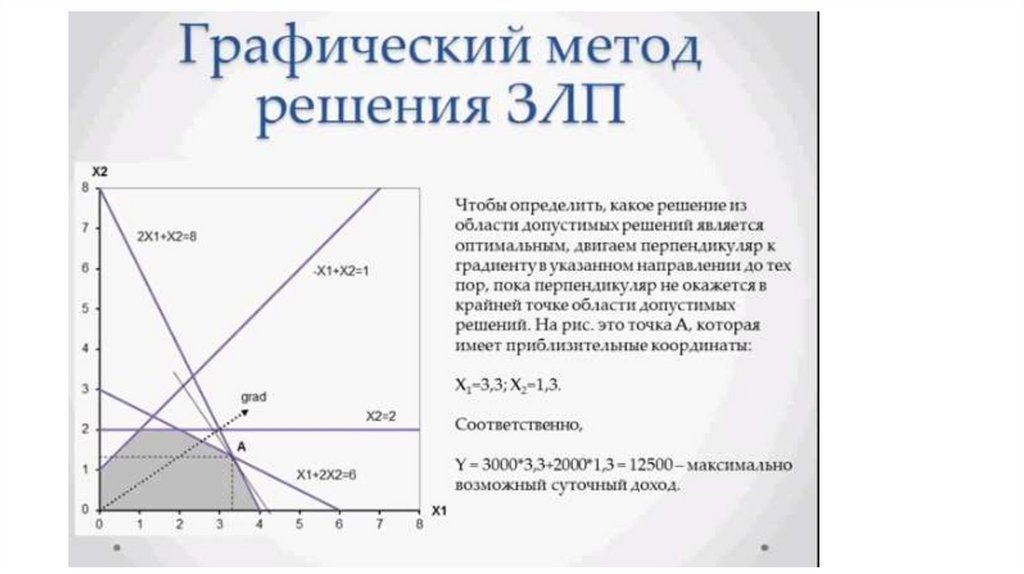
Выводы из графического решения задачи ЛП
• Решение ОЗЛП, если оно существует, не может лежать внутри области допустимых решений, а только на ее
границе.
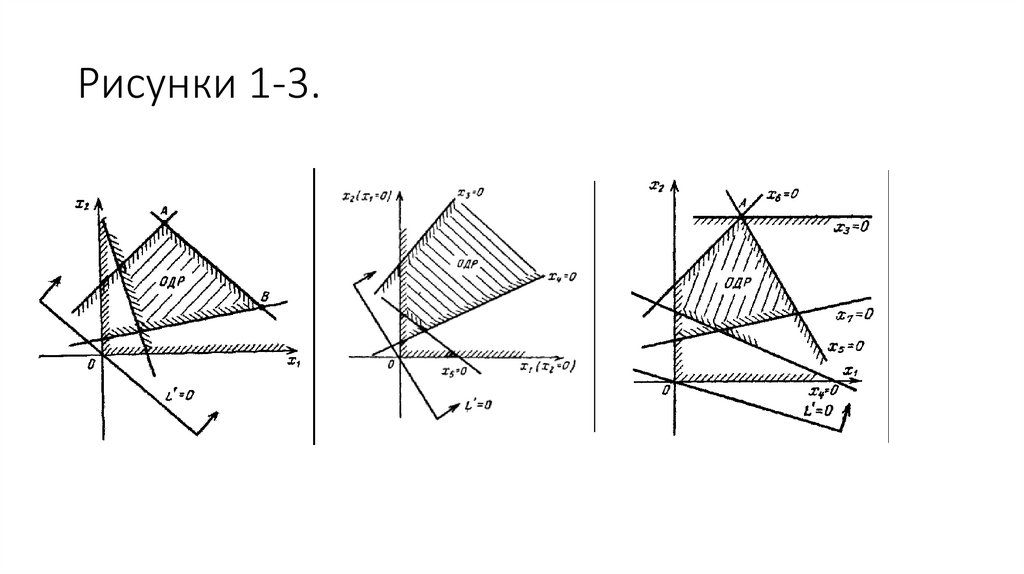
• Решение ОЗЛП может быть и не единственным (см. рис. 1).
• Действительно, если основная прямая параллельна той стороне многоугольника допустимых решений, где
достигается минимум L', то он достигается не в одной точке, а на всей этой стороне. В этом случае ОЗЛП имеет
бесчисленное множество оптимальных решений.
• ОЗЛП может не иметь решения даже в случае, когда существует ОДР (рис. 2)
• Это бывает тогда, когда в направлении стрелок ОДР неограничена, т. е. в области допустимых решений
линейная функция L неограничена снизу. Перемещая основную прямую в направлении стрелок, мы будем
получать все меньшие и меньшие значения L', а значит, и L.
• Решение ОЗЛП, минимизирующее функцию L (оптимальное решение), всегда достигается в одной из вершин
многоугольника допустимых решений {если оно достигается на целой стороне, то оно же достигается и в
каждой из вершин, через которые проходит эта сторона). Решение, лежащее в одной из вершин ОДР,
называется опорным решением, а сама вершина-опорной точкой.
• Для того, чтобы найти оптимальное решение, в принципе достаточно перебрать все вершины ОДР (опорные
точки) и выбрать из них ту, где функция L достигает минимума.
• Если число свободных переменных в ОЗЛП равно n, а число базисных - т и решение ОЗЛП существует, то оно
всегда достигается в точке, где по крайней мере две из переменных x1,x2,...xn обращаются в нуль.
Действительно, в любой опорной точке пересекаются, по крайней мере две из ограничивающих прямых;
однако в ней могут пересекаться и более двух (см. рис. 3).

28.

Рисунки 1-3.

29.

Общая форма задач ЛП

30.

Стандартная форма задач ЛП

31.

Каноническая форма задач ЛП

32.

Переход от стандартной формы к канонической

33.

• https://yandex.ru/video/preview/?text=линейное%20программирование
%20графический%20метод&path=wizard&parentreqid=1611630414607947-697705477479210397100224-prestable-apphost-sas-web-yp-133&wiz_type=vital&filmId=8520333258355464510 (12
мин)
• https://yandex.ru/video/preview/?filmId=8060553222210575960&parentreqid=1611630414607947-697705477479210397100224-prestable-apphost-sas-web-yp133&path=wizard&text=линейное+программирование+графический+м
етод&wiz_type=vital (3 мин)
• https://yandex.ru/video/preview/?filmId=2386671455528984064&from=t
abbar&p=1&parent-reqid=1611630414607947697705477479210397100224-prestable-app-host-sas-web-yp133&text=линейное+программирование+графический+метод (4 мин)

34.

• http://andreyusoft.narod.ru/uchebnik1/part3p2.html
• https://libraryno.ru/laboratornaya-rabota-2-lineynaya-optimizacionnayazadacha-2013_pr_sredstva/
• Таирова Е.В. Линейное программирование: учебное пособие /Е.В
Таирова. – Иркутск: ИрГУПС, 2007. – 75 с.
• https://sdo2.irgups.ru/pluginfile.php/22444/mod_resource/content/1/Лин
ейное%20прог%20Таирова.pdf
• Введение в оптимизацию: учеб. пособие / А.В. Аргучинцев,
А.И.Беников. –Иркутск : Изд-во ИГУ, 2011. –Вып. 3. –105с.
• https://studylib.ru/doc/6226410/arguchincev-a.v.--benikov-a.i.-vvedenie-voptimizaciyu.-uche...

35.

• Харчистов Б.Ф. Методы оптимизации: Учебное пособие.
−Таганрог: Изд-во ТРТУ, 2004. − 140с.
• http://staff.ulsu.ru/semushin/_index/_pilocus/_gist/docs/mycoursew
are/10-optimeth/2-reading/tsure027.pdf