Similar presentations:
Механические колебания и волны (Лекция 1)
1. Механические колебания и волны.
Учебные вопросы:• Понятие колебаний, их основные характеристики
• Классификация механических колебаний
• Кинетическая, потенциальная, полная энергии колебательного
движения.
• Сложение гармонических колебаний направленных вдоль одной
прямой
• Затухающие колебания
• Вынужденные колебания
• Автоколебания
• Механические волны
• Уравнение механических волн и его решение.
• Поток энергии волн. Вектор Умова
• Эффект Доплера и его применение в медицине
• Природа звука. Физические характеристики.
• Характеристики слухового ощущения. Звуковые измерения
• Физические основы звуковых методов исследований в клинике
• Волновое сопротивление. Отражение звуковых волн
2. Понятие колебаний, их основные характеристики.
• Механические колебания - повторяющиесядвижения или изменения состояния
системы (движение маятника, работа
сердца и т. д.)
• Колебания распространяются в среде в
виде волн.
3. Основные характеристики колебаний:
• Амплитуда А – максимальноезначение колеблющейся величины;
• Период Т – время, за которое
происходит одно полное колебание;
• Частота ν – число полных колебаний,
совершаемых в единицу времени.
4. Классификация механических колебаний.
• Свободные колебания (или собственные) –совершаются за счет первоначально
сообщенной энергии;
• Вынужденные колебания – совершаются
за счет постоянно поступающей энергии;
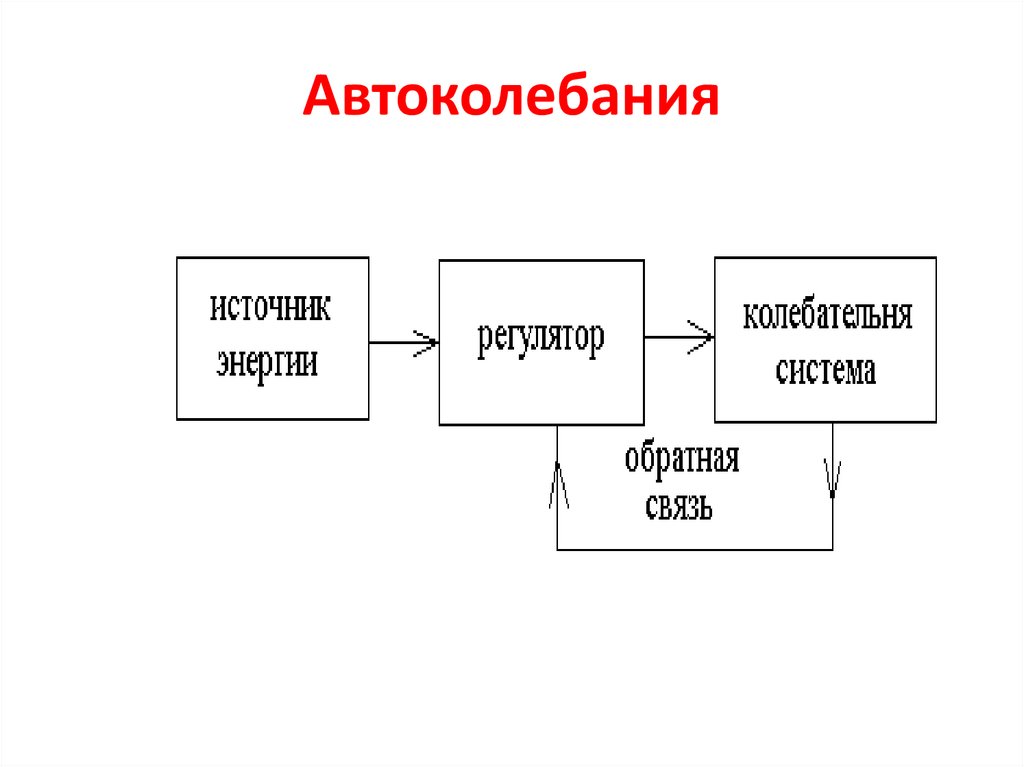
• Автоколебания – совершаются за счет
собственной внутренней энергии;
5. Незатухающие свободные колебания
• колебания, совершаемые колеблющейсясистемой с постоянной амплитудой
d х
2
(1)
х
0
0
2
dt
2
х A cos( 0 t )
(2)
6. Кинетическая, потенциальная, полная энергии колебательного движения.
=Кинетическая, потенциальная, полная
энергии колебательного движения.
2
Ек = 1 / 2kA sin
2
( 0 t 0 )
E П 1 / 2kA cos ( 0 t 0 )
2
E ЕК E П
2
2 2
2
1
/
2
m
1
/
2
kA
=
=
0A
7.
• Вывод формул кинетической,потенциальной и полной
энергий самостоятельно
8. Сложение гармонических колебаний направленных вдоль одной прямой
• х1=А1cos(ω01t+φ01)• х2=А2cos(ω02t+φ01)
• Пусть (ω01= ω02= ω0), тогда
• х=х1+х2= А1cos(ω01t+φ01)+ А2cos(ω02t+φ01)
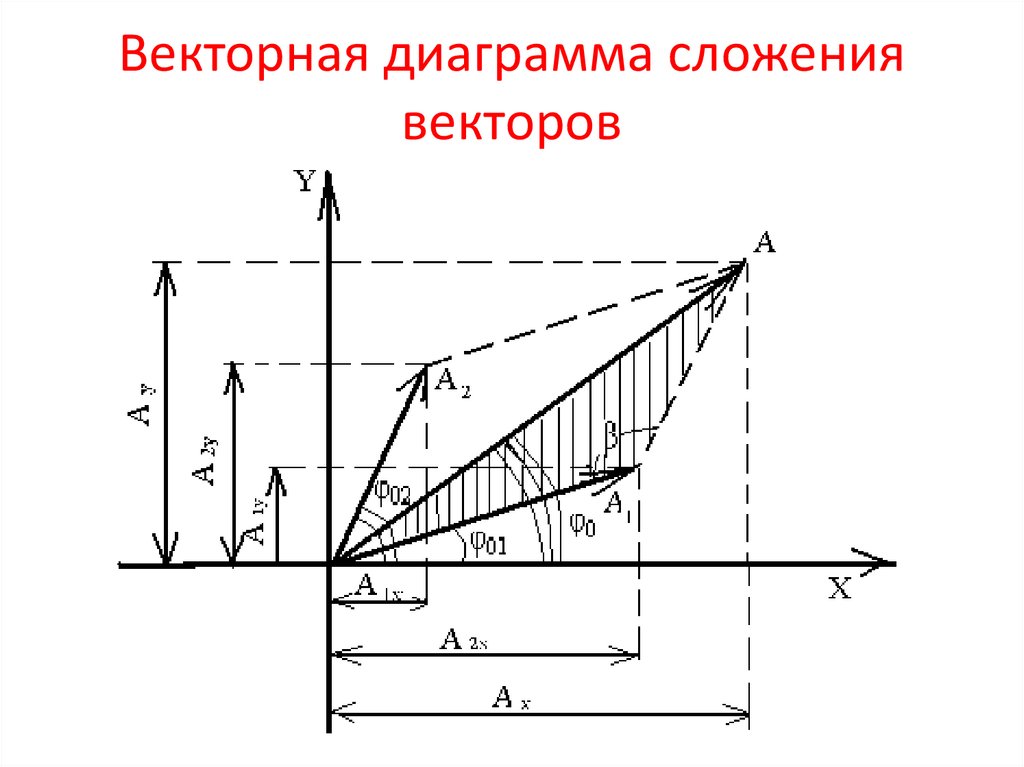
9. Векторная диаграмма сложения векторов
10.
A2 А12 А22 2 А1 А2 cos• Так как –соsβ= - cos[π-(φ02-φ01)]=cos(φ02φ01), то
A
À À 2 À1 À2 cos( 02 01 )
2
1
2
2
11.
• Так как tgφ0 равен отношению проекции А на осьOY к проекции А на ось OX, т.е.
• то Аy/Ax.Учитывая, что проекция равна сумме
проекций, имеем:
• Аy=A1y+A2y=A1sinφ01+A2sinφ02
• Аx=A1x+A2x=A1cosφ01+A2cosφ02
• tgφ0=Ax/Ay=
(A1sinφ01+A2sinφ02)/(A1cosφ01+A2cosφ02)
12. Затухающие колебания
-Затухающие колебания
2
d x
m 2 kx FTP
dt
• Для небольших амплитуд и частот сила
трения равна:
dx
FTP r r
dt
• где: r – коэффициент трения,
характеризующий свойства среды.
Следовательно:
13.
2d x
dx
2
2
0 x 0
2
dt
dt
• где 2β=r/m; = k/m;
• β – коэффициент затухания;
• ω0 – круговая частота собственных
колебаний системы
14. Решение дифференциального уравнения для затухающих колебаний
x A0 et
cos( t 0 )
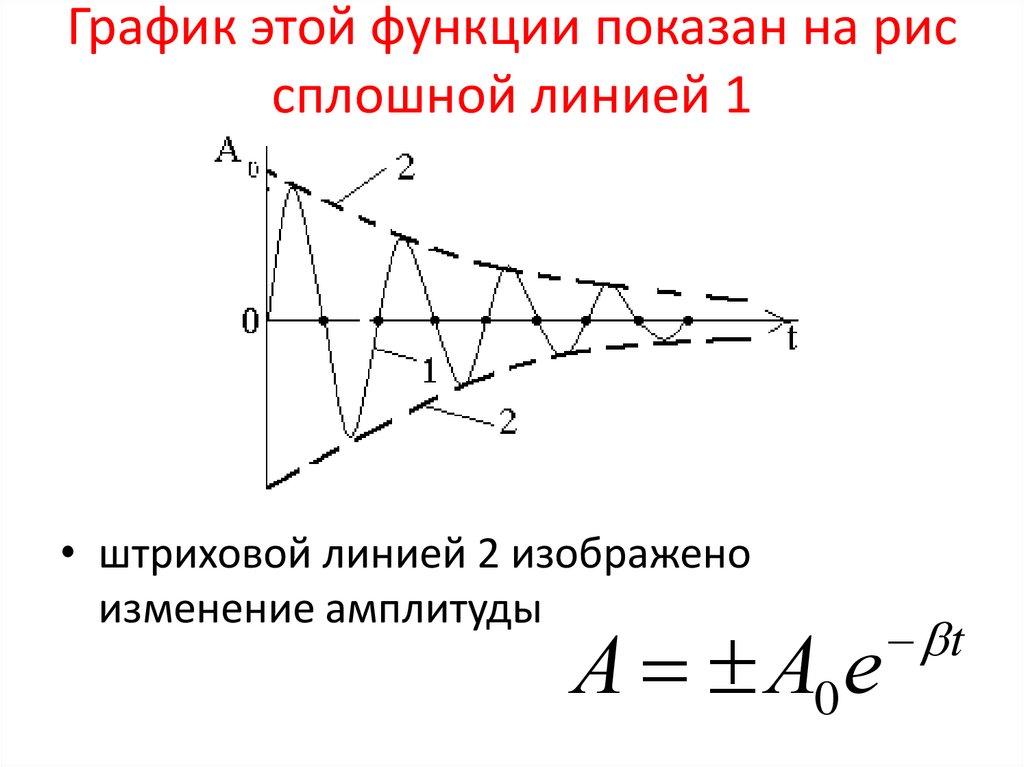
15. График этой функции показан на рис сплошной линией 1
• штриховой линией 2 изображеноизменение амплитуды
А А0 е
t
16.
T2
2
2
0
2
17.
• убывания амплитуды колебанийопределяется коэффициентом затухания.
• Степень затухания часто характеризуют
логарифмическим декрементом
затухания:
A(t )
ln
ln e t
A(t T )
• следовательно:
T
18. Вынужденные колебания
2d x
dx
m 2 kx r F0 cos t
dt
dt
19.
• Решением дифференциального уравненияявляется сумма двух слагаемых.
• Одно из них, соответствующее уравнению
затухающих колебаний, играет роль только
при установлении колебаний. Со временем
им можно пренебречь. Другое слагаемое
описывает смещение материальной точки в
установившихся вынужденных колебаниях:
х=Аcos(ω0t+φ0), где
А = f 0 / ( ) 4 ,
2
0
2 2
2
2
20.
• Если β и ω0 для системы заданы, тоамплитуда вынужденных колебаний
имеет максимальное значение при
некоторой определенной частоте
вынуждающей силы, называемой
резонансной. Само явление –
достижение максимальной амплитуды
для заданных β и ω0 - называют
резонансом.
21.
• Выражения для резонансной частоты иамплитуды имеют вид:
ωрез=
02 2 2
Арез = f0/(2 )
2
0
2
)
22. Автоколебания
23. Механические волны
• Механической волной называютмеханические возмущения,
распространяющиеся в
пространстве и несущие энергию.
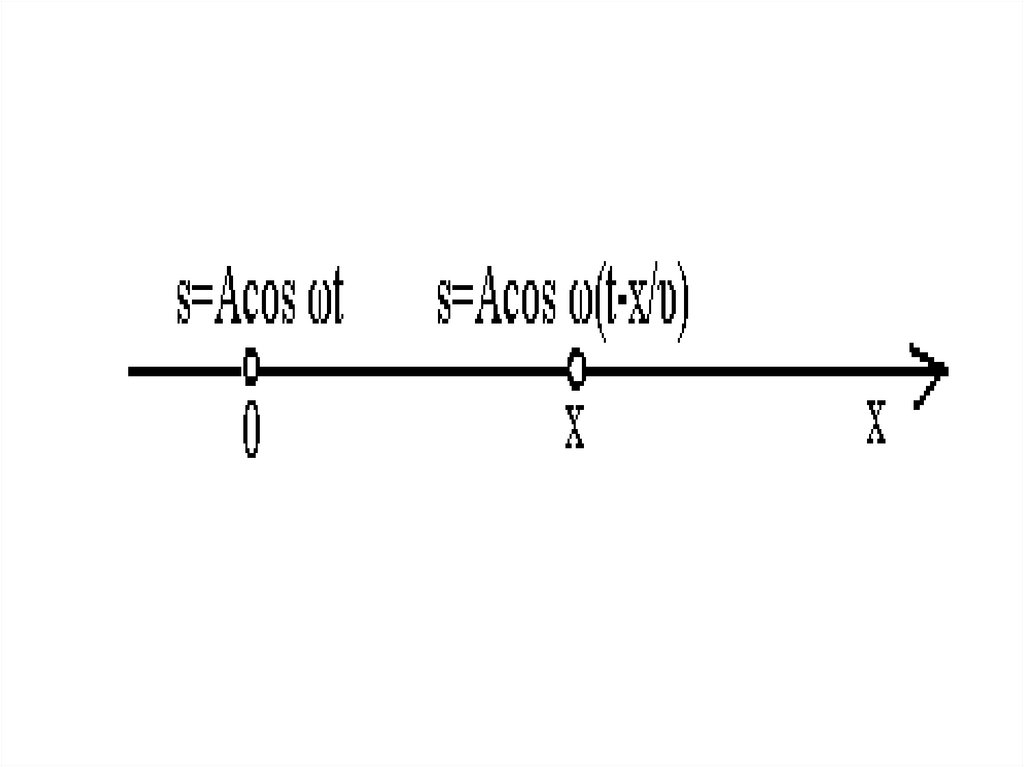
24. Уравнение механических волн и его решение
25.
26. уравнение плоской волны
• S = Acos [ω(t-х/υ)]• где (ωt-х/υ) – фаза
волны
27. волновое уравнение
s 1 s2
2
2
x
t
2
2
28. Поток энергии волн. Вектор Умова
• Волновой процесс связан с распределениемэнергии. Количественной характеристикой
перенесенной энергии является поток
энергии.
• Поток энергии (Ф) – средняя энергия (т. е. за
время, значительно больше периода
колебаний), переносимая волнами в единицу
времени через некоторую поверхность.
Единица измерения потока 1 ватт (Вт).













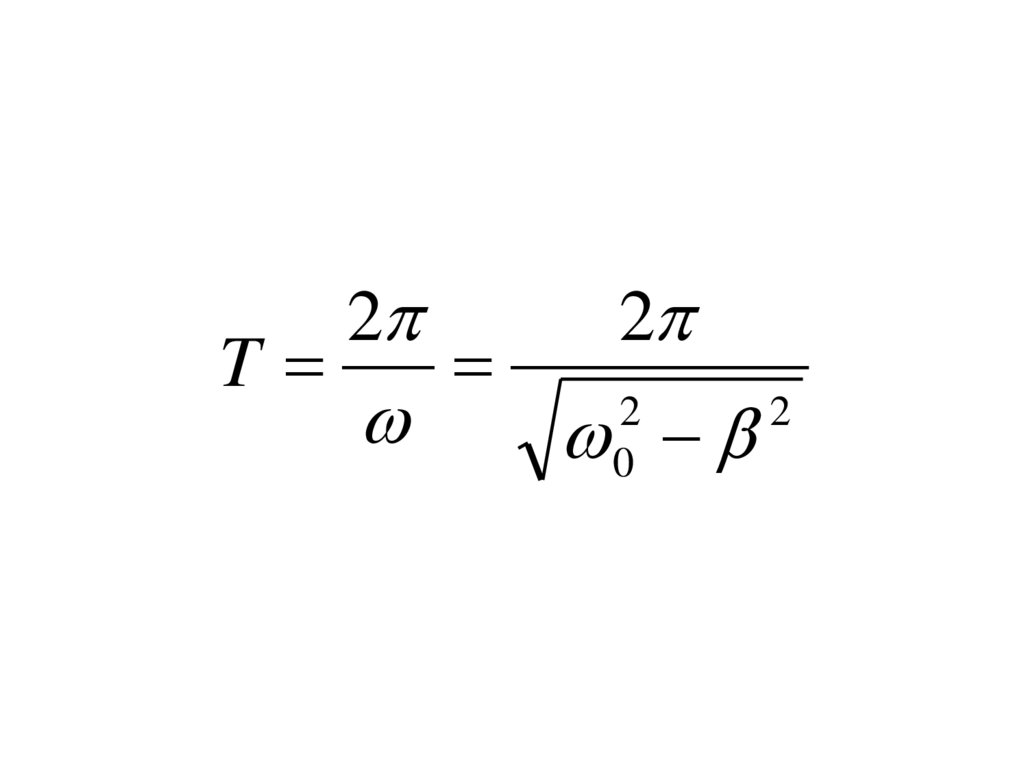










 physics
physics








