Тепловой режим реакторов (Лекция 7)

1.

Лекция 7. ТЕПЛОВОЙ РЕЖИМ РЕАКТОРОВ
Уравнение теплового баланса реактора в общем виде:
Qпр Q расх
Qпр Qс Q р
Q расх Qн Q рм Qт
Qс - количество тепла, поступающее в реактор с сырьевым потоком;
Q p - количество тепла, выделяющееся (для экзотермической реакции) или
поглощаемое (для эндотермической реакции) в результате химической
реакции;
Qн - количество тепла, накапливающееся в реакторе;
Q рм - количество тепла, уносимое из реактора потоком реакционной массы;
Qт - количество тепла, отводимого (или подводимого) извне в результате
теплообмена.
Qc Q p Qн Q рм Qт
Q рм Qс Qк - количество тепла, переносимое конвективным потоком;
Qн Qк Q р Qт
Для экзотермической
реакции
Qн Qк Q р Qт

2.

Математическое выражение теплового баланса на единицу времени, для
элементарного объема реактора и экзотермической реакции (на основе
дифференциального уравнения конвективного теплообмена):
Ср
скорость накопления
тепла в
элементарном
объеме реактора
T
T
C p u
( wA ) H Fуд k T
l
скорость
конвективного
переноса тепла в
элементарном
объеме реактора
скорость подвода
тепла в результате
химической
реакции
– плотность реакционной смеси;
C p – удельная теплоемкость реакционной смеси;
T
– температура реакционной смеси;
u – линейная скорость потока;
l – пространственная координата (длина реактора);
H – тепловой эффект реакции;
Fуд – удельная поверхность теплообмена (на единицу объема реакционной смеси);
K – коэффициент теплопередачи;
T T Tхл , Tхл – температура хладоагента.
скорость отвода
тепла в результате
теплообмена с
внешней средой

3.

1. Реактор идеального смешения
периодического действия
Qk 0
1.1. Политропический режим
dT
Cp
( wA ) H Fуд k T
d
(1)
Характеристическое уравнение РИС-П:
d
С A0
( wA )
0
d
C A0 d
( wA )
( wA )
C A0 d
d
Подставляем (2) в (1):
dT C A0 d
Сp
H Fуд k T
d
d
Поделим уравнение (3) на
C A0
d
, сократим и переставим члены уравнения:
H d
Cp
C A0
(3)
Cp
C A0
dT
Fуд k T
C A0
d
(4)
С p ' – теплоемкость, отнесенная к единице массы исходного реагента.
(2)

4.

Fуд k T
C A0
d
Fуд V p F
Fуд k T VР
C A0 VР
d
F k T
d
N A0
– общая поверхность теплообмена
C A0 V p N A0 – количество вещества
Уравнение теплового баланса РИС-П в политропическом режиме:
F k T
H d C p ' dT
d
N A0
(5)
1.2. Адиабатический режим
В этом режиме теплообмен с внешней средой отсутствует:
Уравнение (5) принимает вид:
T
H d C p ' dT
H d C ' dT
p
0
QТ
F k T
d 0
N A0
(6)
H C p ' T T0
(7)
T0
Уравнения теплового баланса РИС-П в адиабатическом режиме:

5.

Из уравнения (7) следует:
T T0
H
Cp '
При проведении химической реакции до конца, т.е. при α=1:
H
Tmax T0
T0 Tад
Cp '
Tmax
– максимально возможная температура для
экзотермической реакции в адиабатическом режиме;
Tад – адиабатический прирост температуры.
1.3. Изотермический режим
Так как режим в этом аппарате нестационарный, для поддержания постоянной
температуры отвод тепла должен быть переменным по времени, что в промышленных
условиях осуществить сложно. Поэтому изотермические периодические реакторы на
практике не применяются.
2. Реактор идеального вытеснения
2.1. Политропический режим
dT
0 C p u
( wA ) H Fуд k T
dl
dT
( wA ) H C p u
Fуд k T (8)
dl
Qн 0
Характеристическое уравнение РИВ:
d
С A0
( wA )
0
d
C A0 d
( wA )
( wA )
C A0 d
d
(9)

6.

Линейная скорость потока: u
dl
d
(10)
Подставляем (9) и (10) в (8) и после сокращения получаем:
C A0 H d
d
Поделим уравнение (11) на
C A0
d
C A0
u
Cp
C A0
dT
Fуд k T
C A0
d (12)
Сp '
Fуд k T
C A0
Fуд
(11)
:
H d
Cp
dT
Cp
Fуд k T
d
Fуд k T dl
d
C A0
u
F
– поверхность теплообмена в пересчете на единицу длины реактора
F k T
dl
FA0
C A0 FA0 – мольный расход вещества
Уравнение теплового баланса РИВ в политропическом режиме:
'
F
k T
'
H d C p dT
dl
FA0
(13)

7.

2.2. Адиабатический режим
В этом режиме теплообмен с внешней средой отсутствует:
Уравнение (13) принимает вид:
H d C p ' dT
F k T
QТ
dl 0
FA0
Уравнения теплового баланса РИВ в адиабатическом режиме:
H C p ' T T0
H
T T0
Cp '
2.3. Изотермический режим
В этом режиме температура в реакторе постоянна:
Уравнение (13) принимает вид:
T T0 ; dT 0; Qк C p dT 0
F ' k T
H d
dl
FA0
Уравнение теплового баланса РИВ в изотермическом режиме:
(14)

8.

3. Реактор идеального смешения
непрерывного действия
3.1. Политропический режим
В этом реакторе параметры процесса постоянны как во времени, так и в объеме реактора,
поэтому уравнение теплового баланса составляем для всего реактора в целом и параметры
в дифференциальной форме заменяем разностью параметров на входе и на выходе.
Q р Qк Qт
Qн 0
Q р wA H VР
Qр
Характеристическое уравнение РИС-Н:
C A0
( wA )
( wA )
C A0 H VР
C A0 H VР
C A0 H
VР
C A0
T T0
T T0
V p C p T T0
Qk C p u
V p C p
l
u
l
l u
VР
(15)
(16)

9.

Qт Fуд k T V p F k T
(17)
Подставляем (15), (16) и (17) в уравнение теплового баланса:
C A0 H С p T T0 F k T
(18)
Поделим уравнение (18) на С A :
0
H
Сp
Cp
C A0
F k T
T T0
C A0
FA0
Уравнение теплового баланса РИС-Н в политропическом режиме:
F k T
H C T T0
FA0
'
p
(19)
3.2. Адиабатический режим
В этом режиме теплообмен с внешней средой отсутствует:
Уравнение (19) принимает вид:
H C p ' T T0
QТ
F k T
0
FA0

10.

Уравнения теплового баланса РИС-Н в адиабатическом режиме:
H C p ' T T0
T T0
H
Cp '
Примечание: для всех типов реакторов в адиабатическом режиме работы
тепловой баланс выражается одинаковыми уравнениями.
3.3. Изотермический режим
В этом режиме температура в реакторе постоянна:
T T0 ; T T0 0; Qк C p (T T0 ) 0
Уравнение (19) принимает вид:
H
F k T
FA0
Уравнение теплового баланса РИС-Н в изотермическом режиме:
(20)

11.

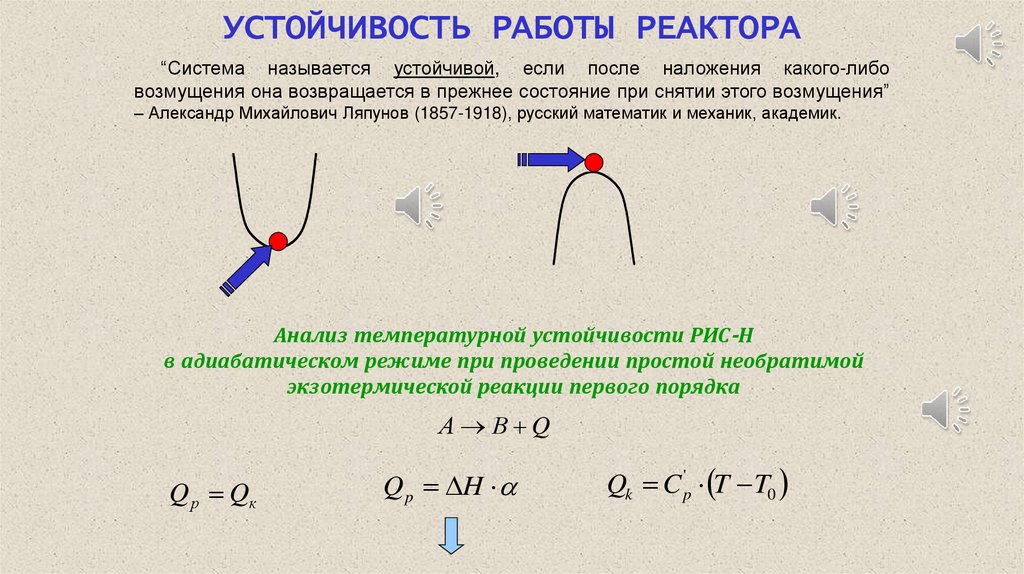
УСТОЙЧИВОСТЬ РАБОТЫ РЕАКТОРА
“Система называется устойчивой, если после наложения какого-либо
возмущения она возвращается в прежнее состояние при снятии этого возмущения”
– Александр Михайлович Ляпунов (1857-1918), русский математик и механик, академик.
Анализ температурной устойчивости РИС-Н
в адиабатическом режиме при проведении простой необратимой
экзотермической реакции первого порядка
А В Q
Q р Qк
Q p H
Qk C p' T T0

12.

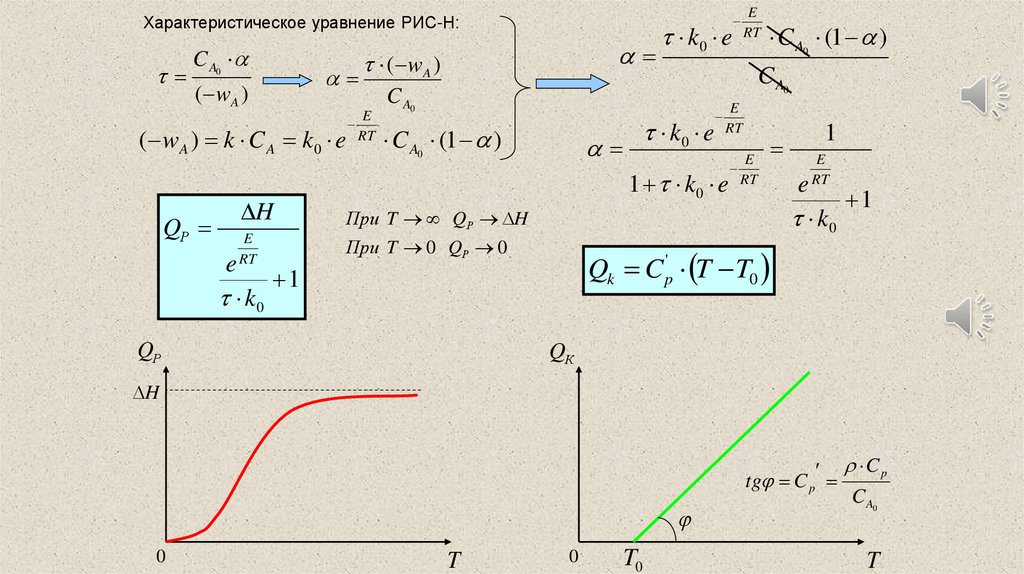
Характеристическое уравнение РИС-Н:
C A0
( wA )
( wA ) k C A k 0 e
QР
( wA )
E
RT
C A0 (1 )
k0 e
E
RT
C A0 (1 )
C A0
C A0
E
RT
E
1 k0 e RT
H
При T QР H
E
RT
При T 0 QР 0
e
1
k0
k0 e
QР
1
E
RT
e
1
k0
Qk C p' T T0
QК
H
tg C p
0
T
0
T0
Cp
C A0
T

13.

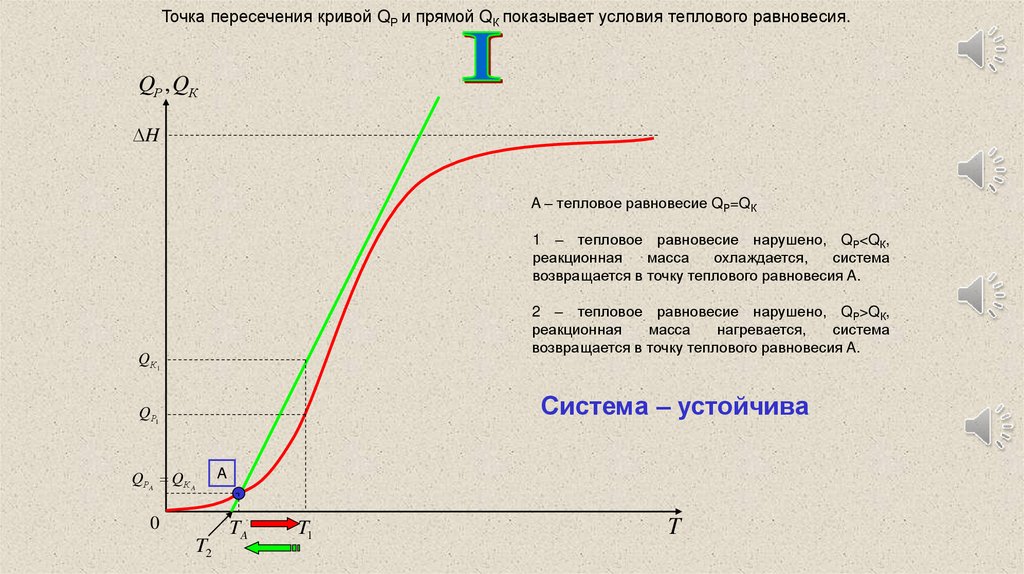
Точка пересечения кривой QР и прямой QК показывает условия теплового равновесия.
QР , QК
H
A – тепловое равновесие QР=QК
1 – тепловое равновесие нарушено, QР<QК,
реакционная
масса
охлаждается,
система
возвращается в точку теплового равновесия A.
2 – тепловое равновесие нарушено, QР>QК,
реакционная
масса
нагревается,
система
возвращается в точку теплового равновесия A.
Q К1
Система – устойчива
QР1
QРA QК A
A
0
T2
TA
T1
T

14.

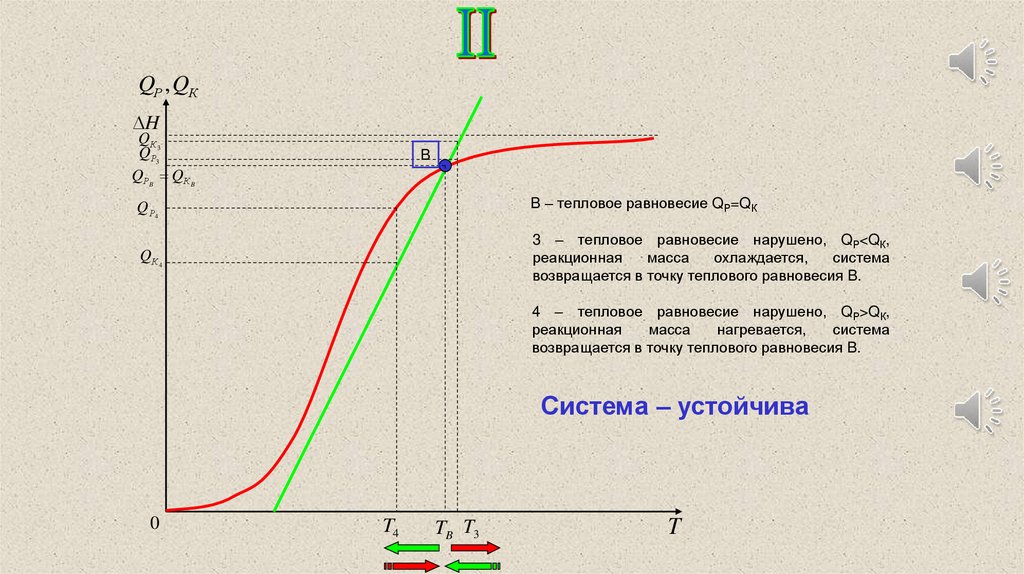
QР , QК
H
QК 3
QР3
QРB QК B
B
Q Р4
B – тепловое равновесие QР=QК
QК 4
3 – тепловое равновесие нарушено, QР<QК,
реакционная
масса
охлаждается,
система
возвращается в точку теплового равновесия B.
4 – тепловое равновесие нарушено, QР>QК,
реакционная
масса
нагревается,
система
возвращается в точку теплового равновесия B.
Система – устойчива
0
T4
TB T3
T

15.

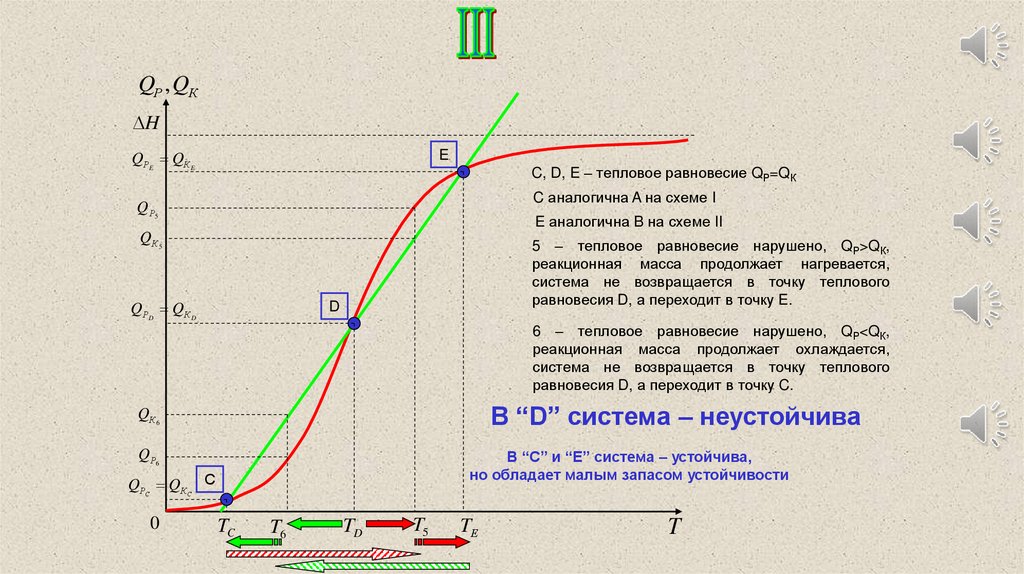
QР , QК
H
QРE QК E
E
C, D, E – тепловое равновесие QР=QК
C аналогична A на схеме I
Q Р5
E аналогична B на схеме II
QК 5
QР D QК D
5 – тепловое равновесие нарушено, QР>QК,
реакционная масса продолжает нагревается,
система не возвращается в точку теплового
равновесия D, а переходит в точку E.
D
6 – тепловое равновесие нарушено, QР<QК,
реакционная масса продолжает охлаждается,
система не возвращается в точку теплового
равновесия D, а переходит в точку C.
В “D” система – неустойчива
QК 6
Q Р6
В “С” и “E” система – устойчива,
но обладает малым запасом устойчивости
QРС QК С С
0
TC
T6
TD
T5
TЕ
T

16.

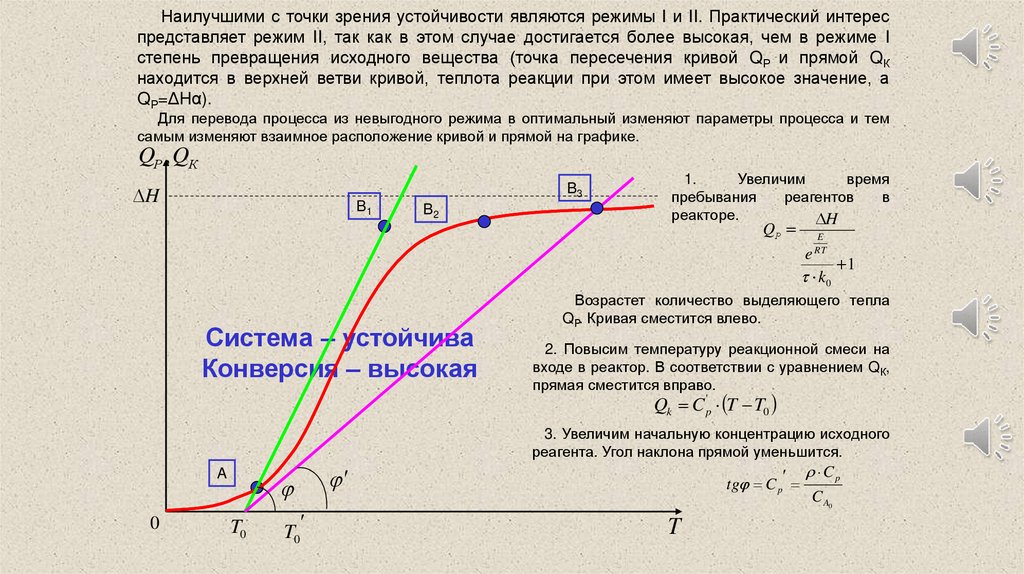
Наилучшими с точки зрения устойчивости являются режимы I и II. Практический интерес
представляет режим II, так как в этом случае достигается более высокая, чем в режиме I
степень превращения исходного вещества (точка пересечения кривой QР и прямой QК
находится в верхней ветви кривой, теплота реакции при этом имеет высокое значение, а
QР=ΔHα).
Для перевода процесса из невыгодного режима в оптимальный изменяют параметры процесса и тем
самым изменяют взаимное расположение кривой и прямой на графике.
QР , QК
H
B3
B1
B2
1.
Увеличим
время
пребывания
реагентов
в
реакторе.
H
QР
E
RT
e
1
k0
Система – устойчива
Конверсия – высокая
Возрастет количество выделяющего тепла
QР. Кривая сместится влево.
2. Повысим температуру реакционной смеси на
входе в реактор. В соответствии с уравнением QК,
прямая сместится вправо.
Qk C p' T T0
3. Увеличим начальную концентрацию исходного
реагента. Угол наклона прямой уменьшится.
A
0
T0
T0
Cp
tg C p
C A0
T

17.

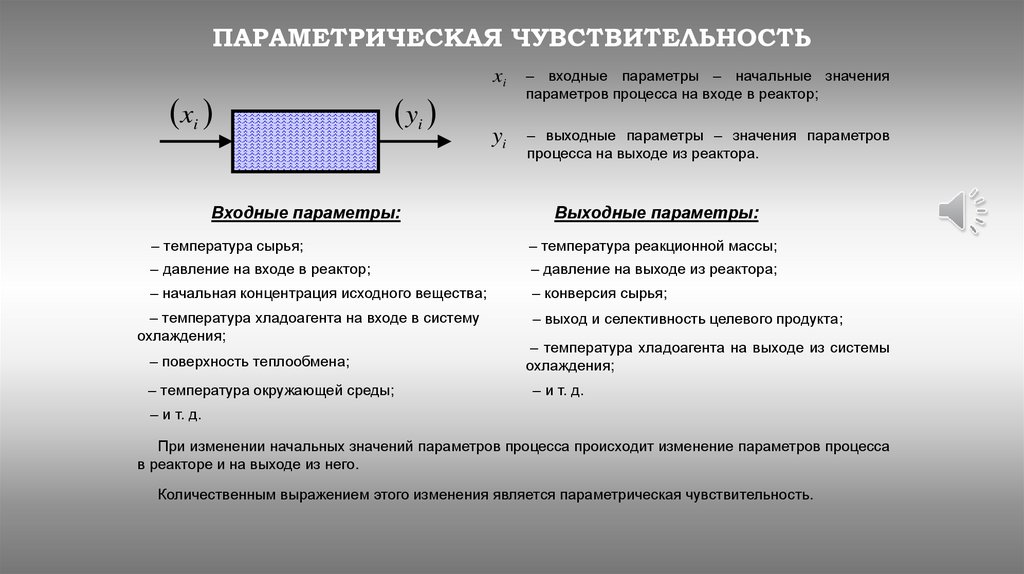
ПАРАМЕТРИЧЕСКАЯ ЧУВСТВИТЕЛЬНОСТЬ
xi
yi
Входные параметры:
xi
– входные параметры – начальные значения
параметров процесса на входе в реактор;
yi
– выходные параметры – значения параметров
процесса на выходе из реактора.
Выходные параметры:
– температура сырья;
– температура реакционной массы;
– давление на входе в реактор;
– давление на выходе из реактора;
– начальная концентрация исходного вещества;
– конверсия сырья;
– температура хладоагента на входе в систему
охлаждения;
– выход и селективность целевого продукта;
– поверхность теплообмена;
– температура хладоагента на выходе из системы
охлаждения;
– температура окружающей среды;
– и т. д.
– и т. д.
При изменении начальных значений параметров процесса происходит изменение параметров процесса
в реакторе и на выходе из него.
Количественным выражением этого изменения является параметрическая чувствительность.

18.

Параметрическая чувствительность – величина, количественно характеризующая
изменение какого-либо выходного параметра процесса при изменении значения какого-либо
входного параметра процесса.
Pij
dy j
dxi
Параметрическая чувствительность – производная выходной величины по входному
параметру.
Чем больше величина параметрической чувствительности, тем сильнее влияет данный входной
параметр на данный выходной. Если параметрическая чувствительность мала, то соответствующий
входной параметр практически на влияет на процесс и с его помощью нельзя процессом управлять. Если
параметрическая чувствительность очень велика, то даже малые колебания входного параметра приводят
к резким колебаниям режима и процесс становится трудноуправляемым (неустойчивым).
Пример: y1 – конверсия сырья;
x1 – температура сырья на входе в реактор;
x2 – давление на входе в реактор;
x3 – концентрация сырья на входе в реактор.
P11
dy1 d
1000 ( );
dx1 dTС
P12
dy1 d
0;
dx2 dPC
P13
dy1
d
10.
dx3 dC A0
Величина параметрической чувствительности зависит от величины входного параметра:
Pij f xi ,
поэтому при изменении входного параметра процесс может попадать в области малой и высокой
параметрической чувствительности.