Химические реакторы. Гетерогенно-каталитические химические процессы

1.

Режимы идеального смешения периодический РИС-п и
идеального вытеснения РИВ с теплообменом
для простой реакции А
В
WА(с,T) = –r(с,T) r c,T r х,T
dx r c, T
d
c0
c0
dT Qp c0 r c, T K т Fуд
T Tx
d
Cp
c0
Cр
при 0
x x0 , T T0
Адиабатический разогрев Qp c0 T
ад
Cp
Параметр теплоотвода
K т Fуд
Cр
B
Система уравнений
приобретает вид:
dx
r x, T
d
dT
Tад r x,T B T Tx
d
при 0
x xн , T Tн
И в общем виде не имеет
аналитического решения.

2.

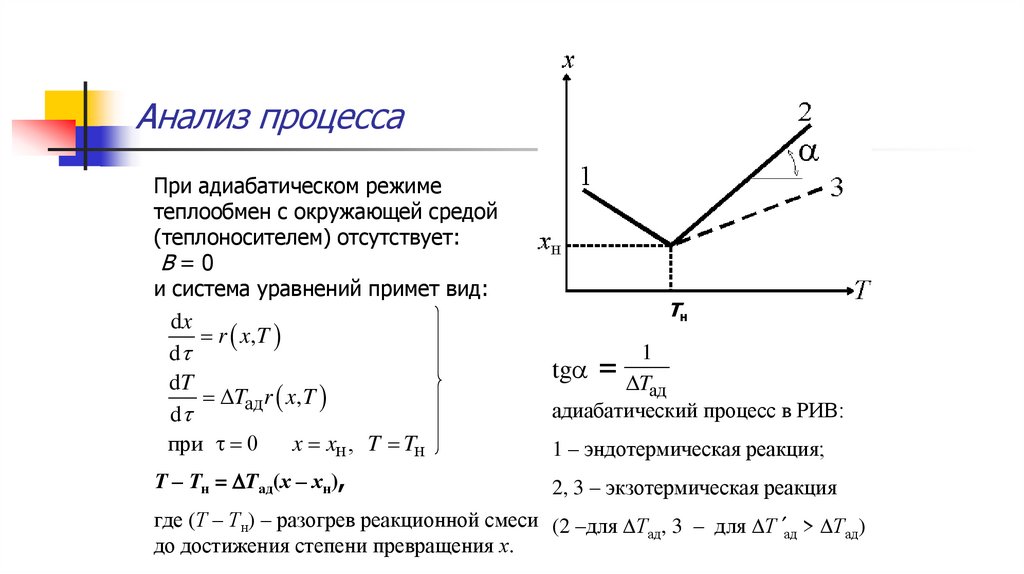
Анализ процесса
При адиабатическом режиме
теплообмен с окружающей средой
(теплоносителем) отсутствует:
В=0
и система уравнений примет вид:
dx
r x, T
d
dT
Tад r x,T
d
при 0
x xн , T Tн
Т – Тн = Tад(х – хн),
Тн
1
tg = T
ад
адиабатический процесс в РИВ:
1 – эндотермическая реакция;
2, 3 – экзотермическая реакция
где (Т – Тн) – разогрев реакционной смеси (2 –для Т , 3 – для Т > Т )
ад
ад
ад
до достижения степени превращения х.

3.

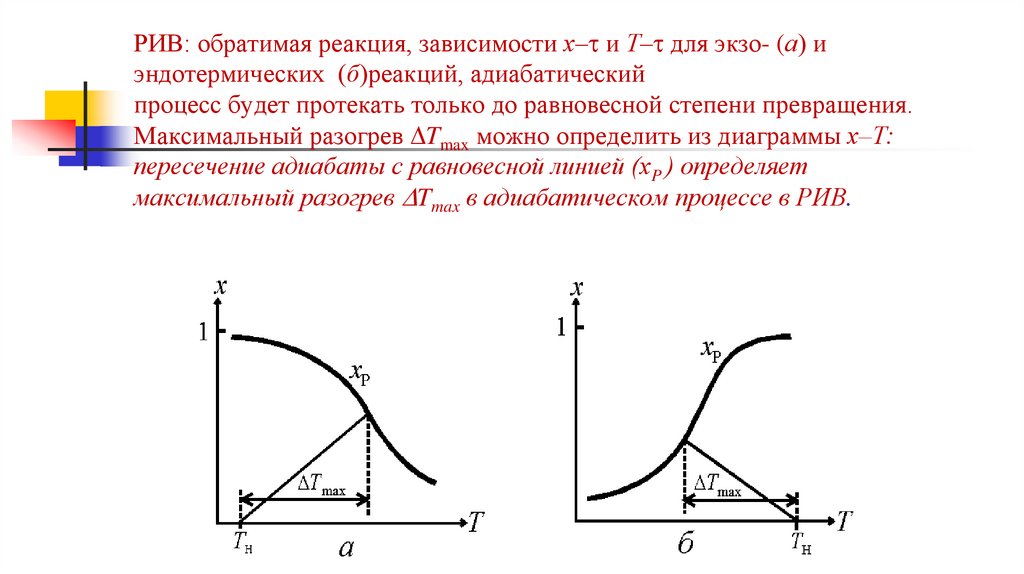
РИВ: обратимая реакция, зависимости х– и Т– для экзо- (а) и
эндотермических (б)реакций, адиабатический
процесс будет протекать только до равновесной степени превращения.
Максимальный разогрев Tmax можно определить из диаграммы х–Т:
пересечение адиабаты с равновесной линией (хP ) определяет
максимальный разогрев Tmax в адиабатическом процессе в РИВ.

4.

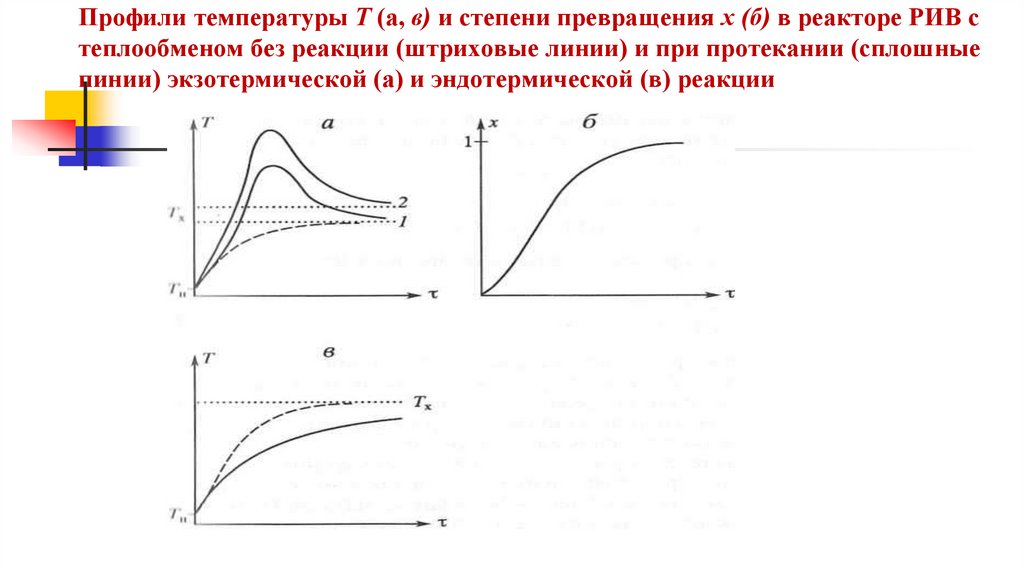
Профили температуры Т (а, в) и степени превращения х (б) в реакторе РИВ с
теплообменом без реакции (штриховые линии) и при протекании (сплошные
пинии) экзотермической (а) и эндотермической (в) реакции

5.

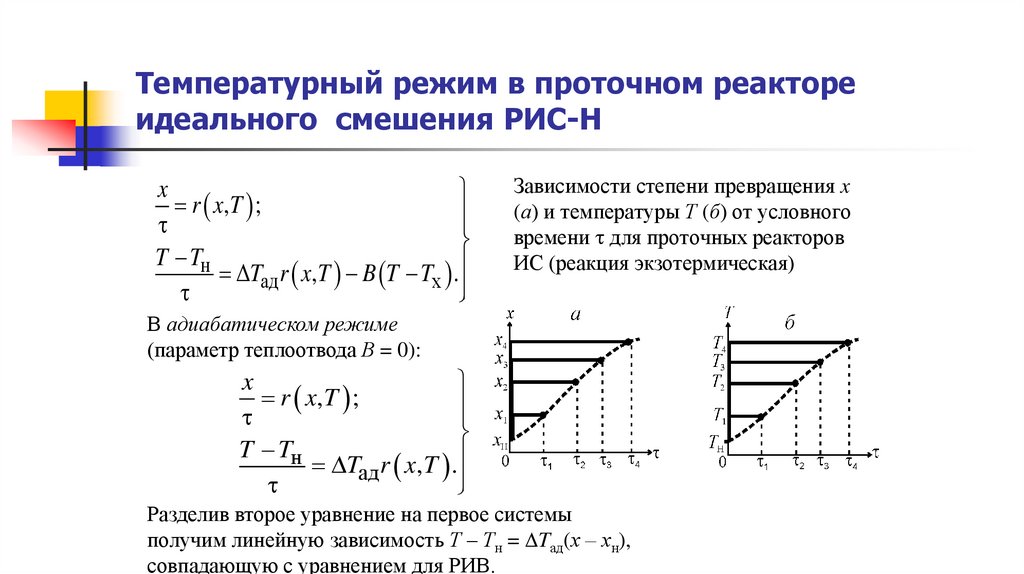
Температурный режим в проточном реакторе
идеального смешения РИС-Н
x
r x, T ;
T Tн
Tад r x,T B T Tx .
Зависимости степени превращения x
(а) и температуры Т (б) от условного
времени для проточных реакторов
ИС (реакция экзотермическая)
В адиабатическом режиме
(параметр теплоотвода В = 0):
x
r x, T ;
T Tн
Tад r x, T .
Разделив второе уравнение на первое системы
получим линейную зависимость Т – Тн = Tад(х – хн),
совпадающую с уравнением для РИВ.

6.

Число и неоднозначность стационарных режимов
Решение системы уравнений – математической модели РИСн в случае протекания в адиабатическом режиме реакции
первого порядка (хн = 0):
x
k T (1 x);
T Tн
Tад k T (1 x)
k T
T Tн Tад
1 k T
qт
qp

7.

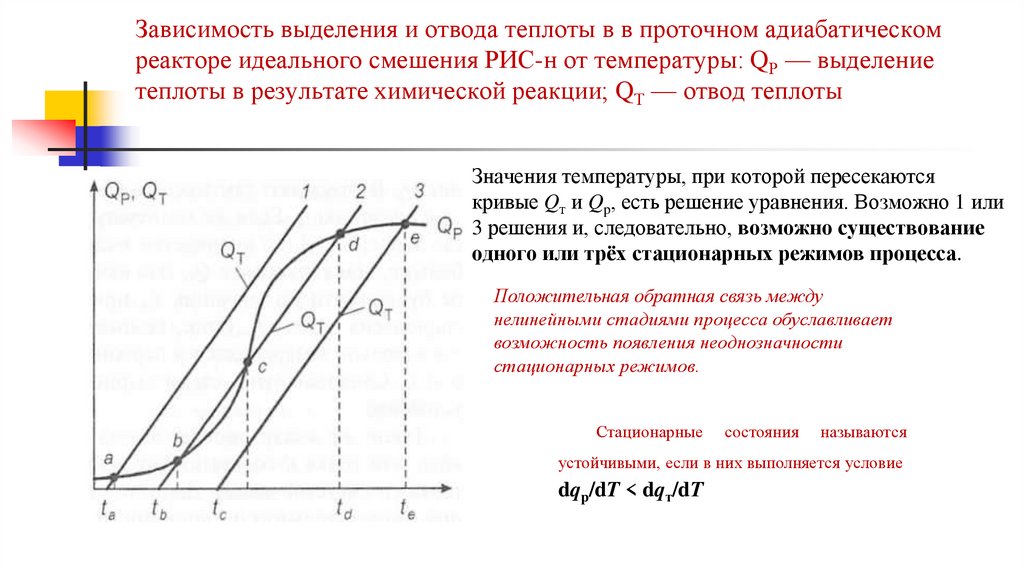
Зависимость выделения и отвода теплоты в в проточном адиабатическом
реакторе идеального смешения РИС-н от температуры: QР — выделение
теплоты в результате химической реакции; QТ — отвод теплоты
Значения температуры, при которой пересекаются
кривые Qт и Qp, есть решение уравнения. Возможно 1 или
3 решения и, следовательно, возможно существование
одного или трёх стационарных режимов процесса.
Положительная обратная связь между
нелинейными стадиями процесса обуславливает
возможность появления неоднозначности
стационарных режимов.
Стационарные
состояния
называются
устойчивыми, если в них выполняется условие
dqp/dT < dqт/dT

8.

Определение устойчивости стационарных состояний: а — устойчивое;
б — неустойчивое; в — устойчивое
Какой режим будет реализован, зависит от предистории пуска процесса.
Если возможно существование трёх режимов и в начале температура в
реакторе будет близка к tb , то установится низкотемпературный режим b.
Если при пуске реактора температура в нём будет высокая, близкая в
величине адиабатического разогрева, то установится высокотемпературный
режим d.
Устойчивое стационарное состояние характеризуется
самопроизвольным восстановлением первоначального состояния системы,
нарушение которого вызвано внешним возмущением

9.

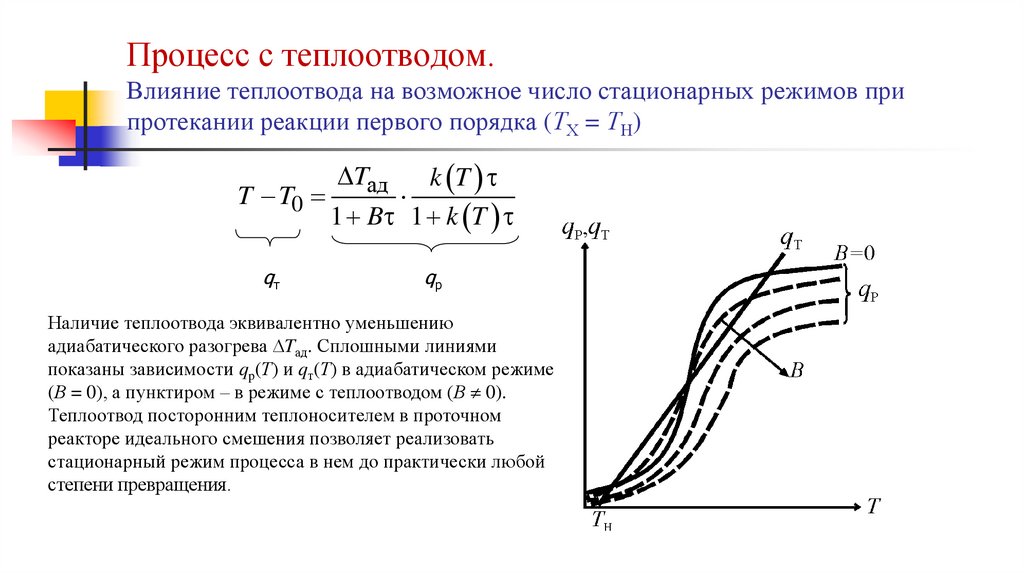
Процесс с теплоотводом.
Влияние теплоотвода на возможное число стационарных режимов при
протекании реакции первого порядка (ТХ = ТН)
k T
T T0
1 B 1 k T
Tад
qт
qp
Наличие теплоотвода эквивалентно уменьшению
адиабатического разогрева Tад. Сплошными линиями
показаны зависимости qp(Т) и qт(Т) в адиабатическом режиме
(В = 0), а пунктиром – в режиме с теплоотводом (В 0).
Теплоотвод посторонним теплоносителем в проточном
реакторе идеального смешения позволяет реализовать
стационарный режим процесса в нем до практически любой
степени превращения.

10.

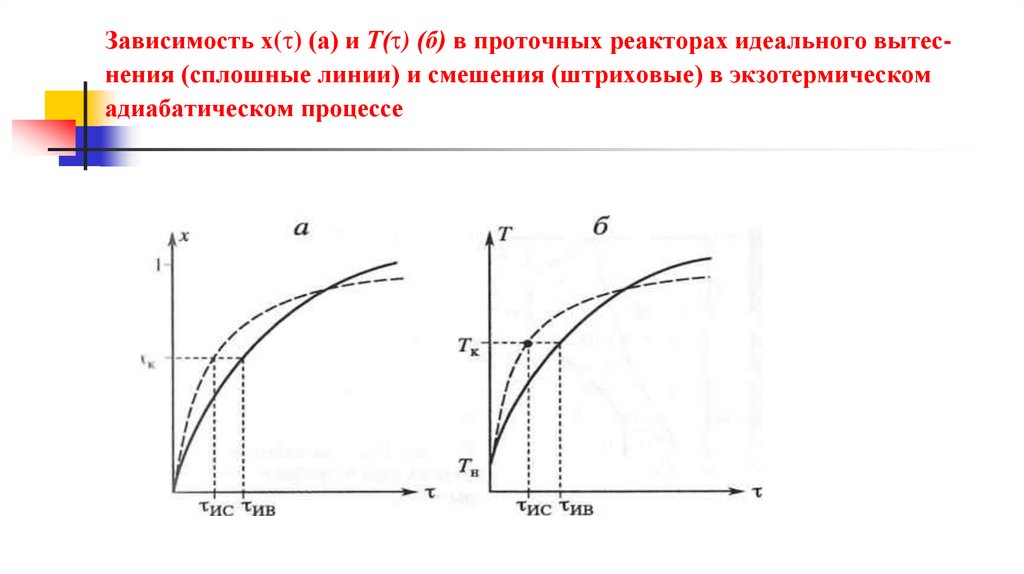
Зависимость х( ) (а) и Т( ) (б) в проточных реакторах идеального вытеснения (сплошные линии) и смешения (штриховые) в экзотермическом
адиабатическом процессе

11.

Автотермический реактор.
Процесс в таком реакторе – адиабатический (в системе отсутствует
посторонний теплоноситель). Разность температур между входным и
выходным потоками равна адиабатическому разогреву Тадх. Такой режим
и реактор называют автотермическими.
Роль теплоносителя выполняет
исходная реакционная смесь, которая
подается в трубки реактора и
нагревается теплотой, выделяющейся
в ходе экзотермической реакции.
Математическая модель
процесса.
Нагрев реакционной смеси в трубках
представлен уравнением:
Cp
dTx
K T Fx,уд Tx T
d x
где Т, Тх – температура в реакционной зоне и в трубках соответственно;
v
x x – условное время пребывания потока в трубках; vх – объём трубок;
V0
F
– поверхность теплообмена, отнесенная к единице объёма трубок
F1,уд T
vx

12.

Перейдём от переменных х и параметра Fх,уд
Математическая модель
процесса в автотермическом
реакторе:
dx
r x, T ;
d
dx
Tад r x, T B T TX ;
d
dTX
B T TX ;
d
при 0 T TX , x xн ;
при к TX Tн
.
к
vp
V0
и Fуд:
FT
vP
Неоднозначность стационарного
режима.
В этом реакторе можно проследить
положительную обратную связь по теплу
между выходящим и входящим потоками
через стенки трубок. При наличии
обратной связи при некоторых условиях
процесса возможно возникновение
неоднозначности стационарного режима
– возможность существования трёх
стационарных режимов при одной
температуре потока на входе в реактор
Т Н.

13.

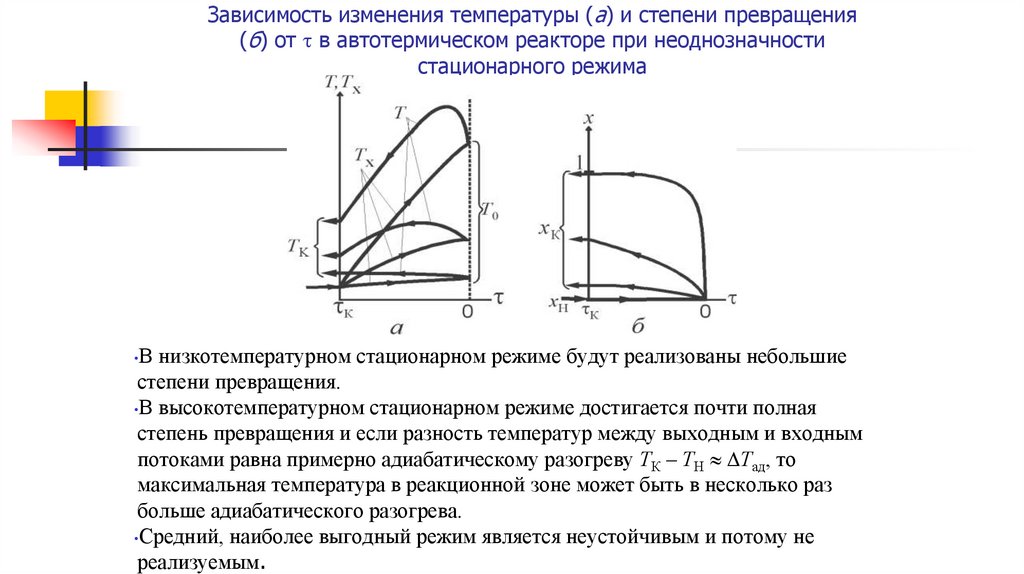
Зависимость изменения температуры (а) и степени превращения
(б) от в автотермическом реакторе при неоднозначности
стационарного режима
В низкотемпературном стационарном режиме будут реализованы небольшие
степени превращения.
•В высокотемпературном стационарном режиме достигается почти полная
степень превращения и если разность температур между выходным и входным
потоками равна примерно адиабатическому разогреву ТК – ТН Тад, то
максимальная температура в реакционной зоне может быть в несколько раз
больше адиабатического разогрева.
•Средний, наиболее выгодный режим является неустойчивым и потому не
реализуемым.