Similar presentations:
Электростатика. Закон Кулона
1.
Карагандинский технический университе им. А.СагиноваКафедра физики
Тема лекции:
Электростатика.
Для всех
специальностей
2. План лекции.
3. Электрические заряды. Закон Кулона.
Английский врач Джильберт (конец XVI в.) назвал тела,способные после натирания притягивать легкие предметы,
наэлектризованными.
В природе, существует только два типа электрических зарядов:
заряды, подобные возникающим
на стекле, потертом о кожу (их
назвали положительными),
и заряды, подобные возникающим
на эбоните, потертом о мех (их
назвали отрицательными).
Одноименные заряды друг от
друга отталкиваются,
разноименные — притягиваются.
4.
Опытным путём (1910—1914) американский физикР. Милликен (1868—1953) показал, что электрический заряд
дискретен, т.е. заряд любого тела составляет целое кратное от
элементарного заряда.
q ne
e = -1,6∙10-19 Кл
me=9,11∙10-31 кг
Закон сохранения электрических зарядов.
Алгебраическая сумма электрических зарядов
любой замкнутой системы остаётся неизменной.
q q1 q2 q3 ... qn const
Единица электрического заряда — кулон (Кл) — электрический
заряд, проходящий через поперечное сечение проводника при
силе тока 1 А за время 1 с.
5.
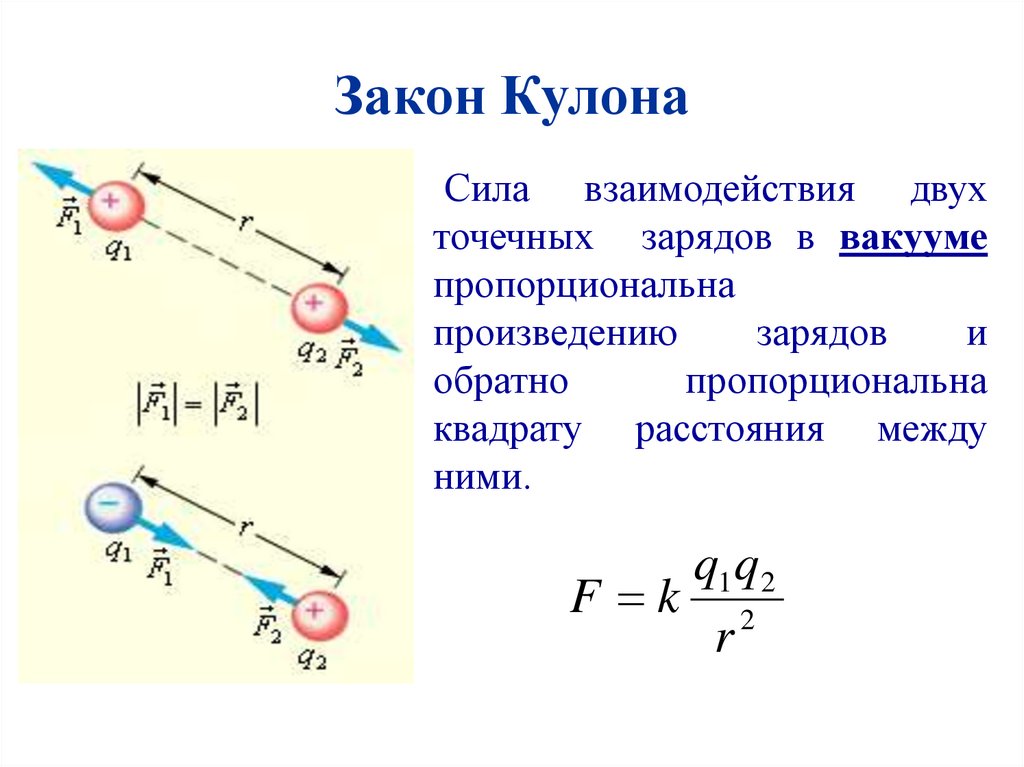
Закон КулонаСила взаимодействия двух
точечных зарядов в вакууме
пропорциональна
произведению
зарядов
и
обратно
пропорциональна
квадрату расстояния между
ними.
q1q 2
F k 2
r
6. Закон Кулона
kq1q 2
F k 2
r
1
k 9 10
4 0
2
н
м
9
Кл 2
q1q2
F
2
4 0 r
1
0 8,85 10
12
Кл /( H м )
2
- электрическая постоянная
2
7.
1q1q2
F
2
4 0 r
- Закон Кулона для диэлектриков
q1q2
F k 2
r
ε –диэлектриктрическая проницаемость
F0
F
- Диэлектрическая проницаемость показывает
во сколько раз сила взаимодействия между
зарядами в вакууме больше чем в данной среде.
F0- сила взаимодействия в вакууме,
F – сила взаимодействия в среде
8.
Электростатическое поле. Напряженностьэлектростатического поля
Взаимодействие между зарядами происходит посредством
электрического поля. Наличие электрического поля определяется
зарядом. Это точечный единичный положительный заряд,
называемый пробным зарядом. Если электрическое поле создается
неподвижным зарядом, то это электростатическое поле.
Пусть электрическое поле создается зарядом q. Введем в это поле
точечный положительный заряд q0. На эту точку со стороны поля
действует сила F. В каждой точке поля сила разная. А отношение
F/q0 будет одинаковым и характеризует поле.
q
q0
q
q0
9. Электростатическое поле. Напряженность электростатического поля
qq0
E F / q0
q
q0
q0 - пробный заряд
В
м
Н
Кл
Напряженность электростатического поля в данной точке есть
физическая величина, определяемая силой, действующей на
единичный положительный заряд, помещенный в эту точку поля.
Напряженность - силовая характеристика поля. Напряженность
поля точечного заряда в вакууме
q
E k 2.
r
1
q
E
.
2
4 0 r
10.
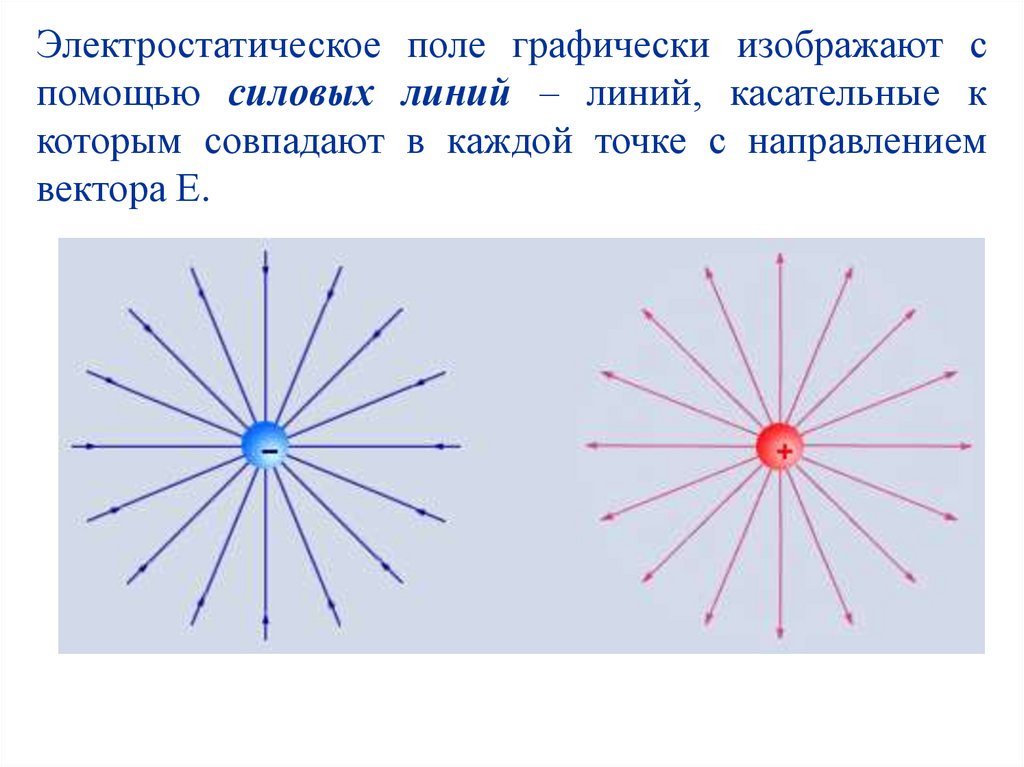
Электростатическое поле графически изображают спомощью силовых линий – линий, касательные к
которым совпадают в каждой точке с направлением
вектора Е.
11.
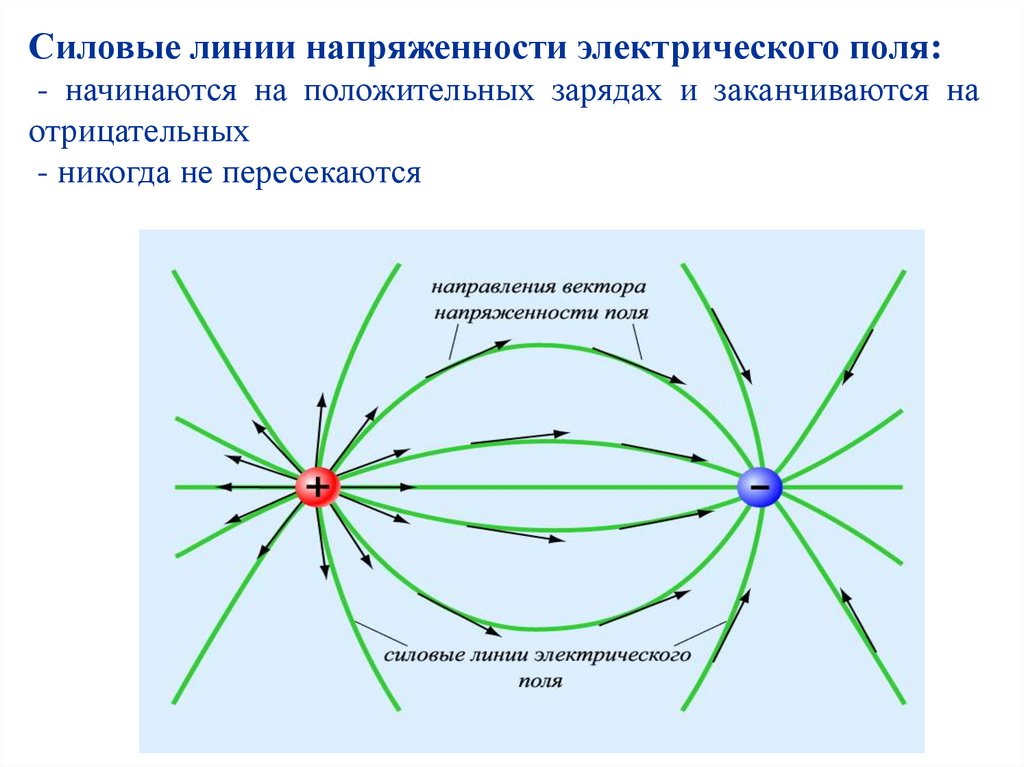
Силовые линии напряженности электрического поля:- начинаются на положительных зарядах и заканчиваются на
отрицательных
- никогда не пересекаются
12.
Принцип суперпозицииНапряженность результирующего поля равна геометрической
сумме напряженностей полей, создаваемых в данной точке
каждым из зарядов в отдельности.
n
E Ei
i 1
q0
E E1 E2 ... En Ei
13.
Поток вектора напряженностиэлектростатического поля
Потоком вектора напряженности
через площадку dS называется
величина равная числу линий
напряженности, пронизывающих
площадку dS (Ф).
dФЕ EdS cos Еn dS
EdS
S
Поток вектора Е сквозь произвольную замкнутую поверхность
E Поток вектора напряжения
14.
Поток вектора напряженностиэлектростатического поля
dФЕ EdS cos Еn dS
ФЕ Еn dS
s
dS dSn
Единица потока вектора
напряженности
электростатического
поля — 1 В м
15.
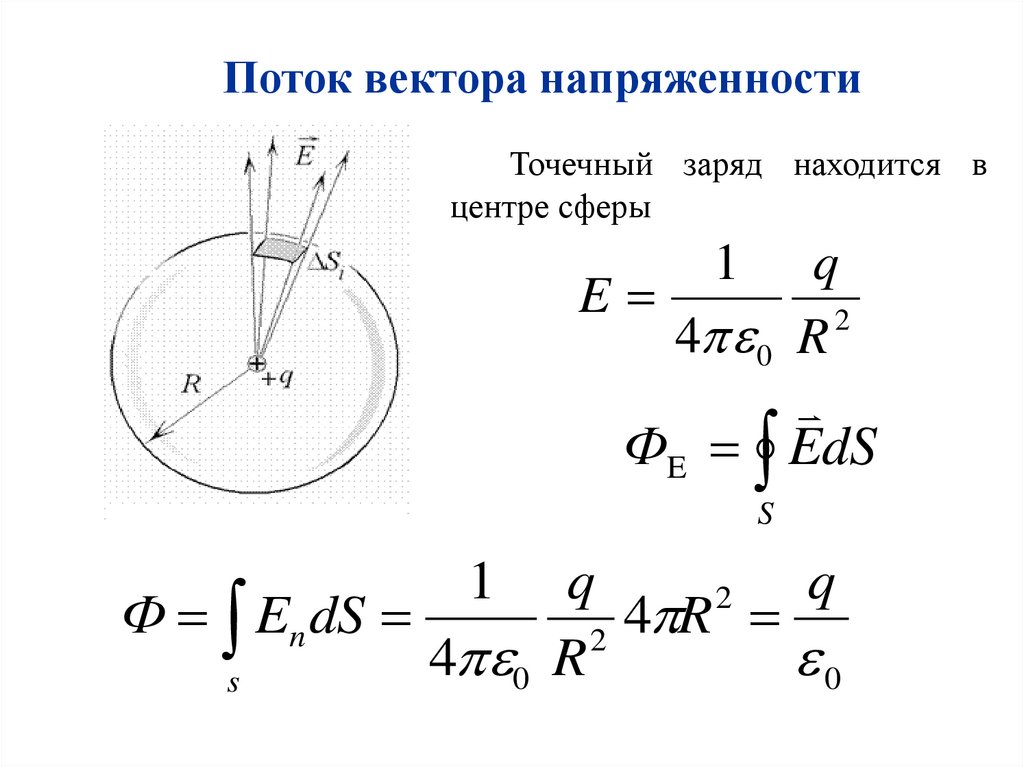
Поток вектора напряженностиТочечный заряд находится в
центре сферы
1
q
E
4 0 R 2
ФE EdS
S
1
q
q
2
Ф En dS
4 R
2
4 0 R
0
s
16. Теорема Гаусса для электростатического поля в вакууме
Теорема К. Гаусса определяет поток вектора напряженностизлектрического поля
сквозь произвольную замкнутую
поверхность.
q/ε0
1 n
EdS En dS q
S
S
0 i 1
i
Знак потока совпадает со
знаком заряда.
Если внутри поверхности нет зарядов, то поток вектора Е
будет равен нулю
17.
Теорему Гаусса для электростатического поля ввакууме можно представить в таком виде:
1 n
EdS En dS q
S
0 i 1
S
если заряд распределен в пространстве
с объемной плотностью заряда
dq
dV
[Кл/м3]
E
dS
n
S
dq dV q dV
1
0
dV
Применим теорему Гаусса к расчету электростатических полей
в вакууме
18. Поле равномерно заряженной бесконечной плоскости.
Поверхностнаяплотность заряда, заряд,
приходящий на единицу
площади поверхности
q
S
q S
[Кл/м2]
19.
q SФЕ 2E S
2 E S
q
0
E n / 2 0
ФE q / 0
S
2 E S
0
2E
0
- напряженность поля равномерно
заряженной бесконечной плоскости
20. Поле двух бесконечных параллельных разноименных заряженных плоскостей.
E1 E 2, E A E1 E 2
2 0
EA E1 E2 0
EС E1 E2
EС E1 E2 0
E В E1 E 2
E В E1 E 2 2
2 0 0
EВ / 0
21.
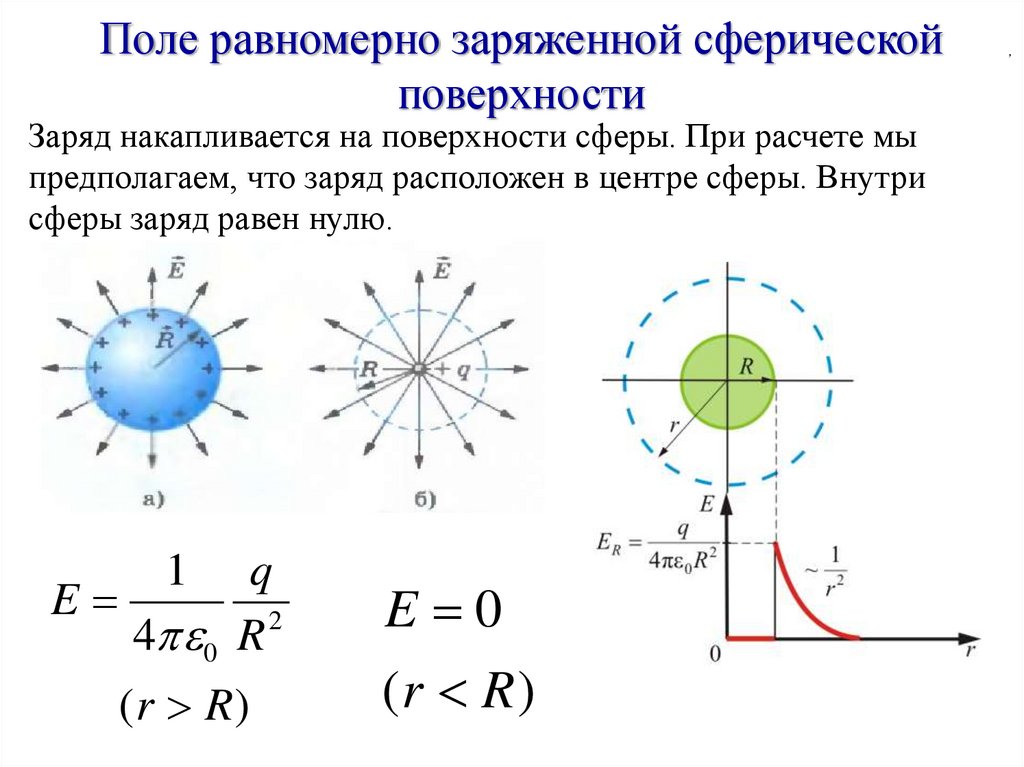
Поле равномерно заряженной сферическойповерхности
Заряд накапливается на поверхности сферы. При расчете мы
предполагаем, что заряд расположен в центре сферы. Внутри
сферы заряд равен нулю.
1
q
E
2
4 0 R
(r R)
E 0
(r R )
,
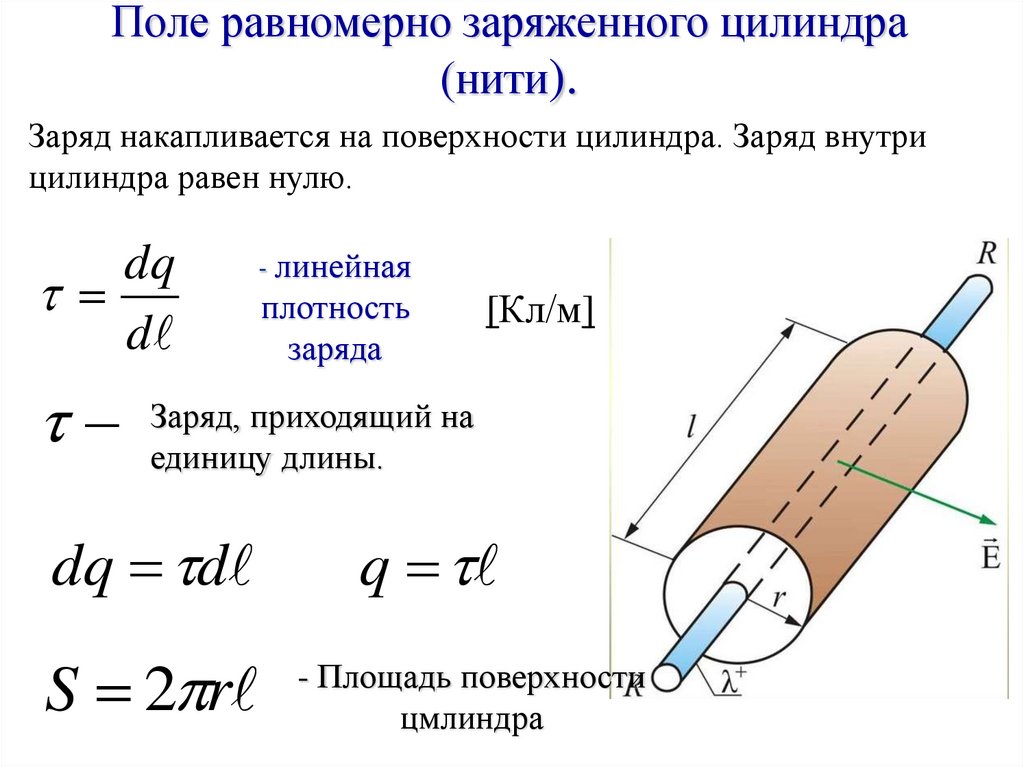
22.
Поле равномерно заряженного цилиндра(нити).
Заряд накапливается на поверхности цилиндра. Заряд внутри
цилиндра равен нулю.
dq
d
- линейная
плотность
заряда
[Кл/м]
приходящий на
Заряд,
единицу длины.
dq d
S 2 r
q
- Площадь поверхности
цмлиндра
23.
Используем теорему Гаусса:ФE E n dS q / 0
S
1
E
2 0 r
E 2 r
0
(r R)
Если r<R, то замкнутая поверхность внутри зарядов не
содержит, поэтому в этой области E=0.
E 0
(r R )
24.
Работа электростатического поляЕсли в электростатическом поле точечного заряда q из точки 1 в
точку 2 вдоль произвольной траектории перемещается другой
точечный заряд q0, то сила, приложенная к заряду, совершает
работу. Работа силы F на элементарном перемещении dl равна
25. Циркуляция вектора напряженности электростатического поля
Работа, совершаемая при перемещении электрического заряда вовнешнем электростатическом поле по любому замкнутому пути L,
равна нулю
dA 0
q0 1Кл
L
A12 q0 Ed 0
Интеграл
( Е dl ) 0
l
называется циркуляцией вектора напряженности.
26.
Потенциальная энергия поляТело, находящееся в потенциальном поле сил,
обладает потенциальной энергией, за счет которой
силами
поля
совершается
работа.
Работа
консервативных сил совершается за счет убыли
потенциальной энергии.
Работу сил электростатического поля при перемещении
заряда q0 из точки 1 в точку 2 определим как разность
потенциальных энергий, которыми обладает заряд q0 в
начальной и конечной точках поля заряда q:
qq0
1 qq0
A12
W p1 W p 2
4 0 r1
4 0 r2
1
27. Потенциал электростатического поля
Потенциальная энергия заряда q0 в поле заряда q на расстоянииr от него равна
1 qq
WP
4 0 r
0
k
0
r
Отношение W/q0 не зависит от q0 и является
энергетической характеристикой электростатического поля, называемой потенциалом
W
q0
Потенциал в какой-либо точке электростатического поля есть
физическая величина, определяемая потенциальной энергией
единичного положительного заряда, помещенного в эту точку.
Потенциал поля точечного заряда
q
k
r
1
q
4 0 r
28.
Работа, совершаемая силами электростатического поля приперемещении заряда q0 из точки 1 в точку 2, может быть
представлена как
A12=Wp1- Wp2=q0(φ1 - φ2).
Разность потенциалов двух точек 1 и 2 в электростатическом
поле определяется работой, совершаемой силами поля, при
перемещении единичного положительного заряда из точки 1 в
точку 2.
Потенциал — физическая величина, определяемая работой по
перемещению единичного положительного заряда при удалении
его из данной точки поля в бесконечность
A
q0
29.
A12 q0 EdA12 q0 ( 1 2 )
q0 1 2 q0 Ed
2
1 2 Ed
1
1 2 El
30.
1 2 Ed1 2 U
1 2 -разность потенциалов
U - напряжение
U Ed
E U / d
W q
Потенциальная
энергия
- Связь между напряжением и
напряженностью
В
м
31. Связь между вектором напряженности электрического поля и потенциалом φ
E gradНапряженность Е поля равна градиенту потенциала со знаком
минус. Знак минус определяется тем, что вектор напряженности
Е поля направлен в сторону убывания потенциала:
E
i
j
k
y
z
x
Для графического изображения распределения потенциала
электростатического поля, как и в случае поля тяготения,
пользуются эквипотенциальными поверхностями —
поверхностями, во всех точках которых потенциал имеет
одно и то же значение
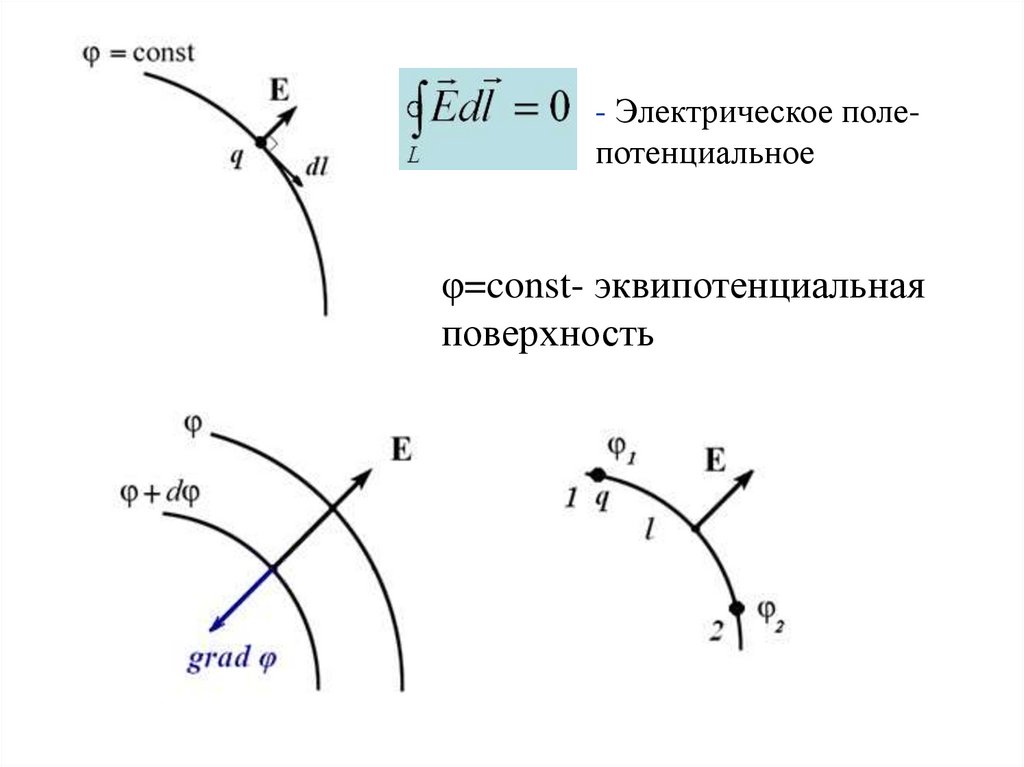
32.
- Электрическое полепотенциальноеφ=const- эквипотенциальная
поверхность
33.
Электрическое поле вдиэлектриках
Виды диэлектриков:
•Полярные
•Неполярлные
•Ионные
34.
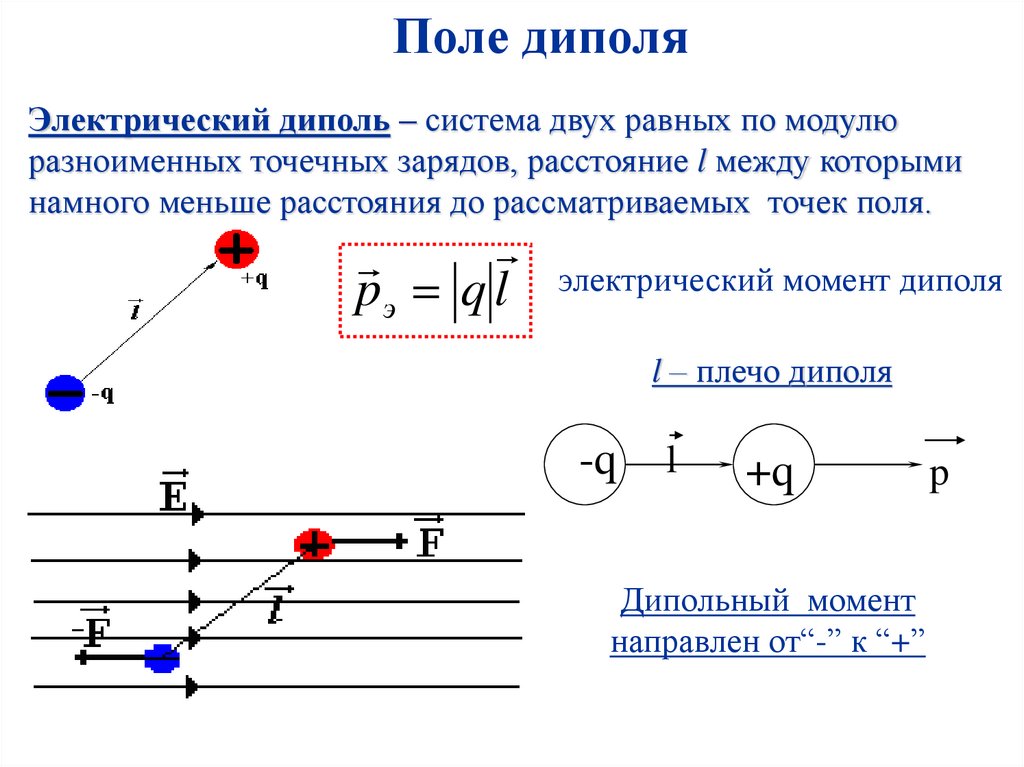
Поле диполяЭлектрический диполь – система двух равных по модулю
разноименных точечных зарядов, расстояние l между которыми
намного меньше расстояния до рассматриваемых точек поля.
pэ q l
электрический момент диполя
l – плечо диполя
-q
l
+q
Дипольный момент
направлен от“-” к “+”
p
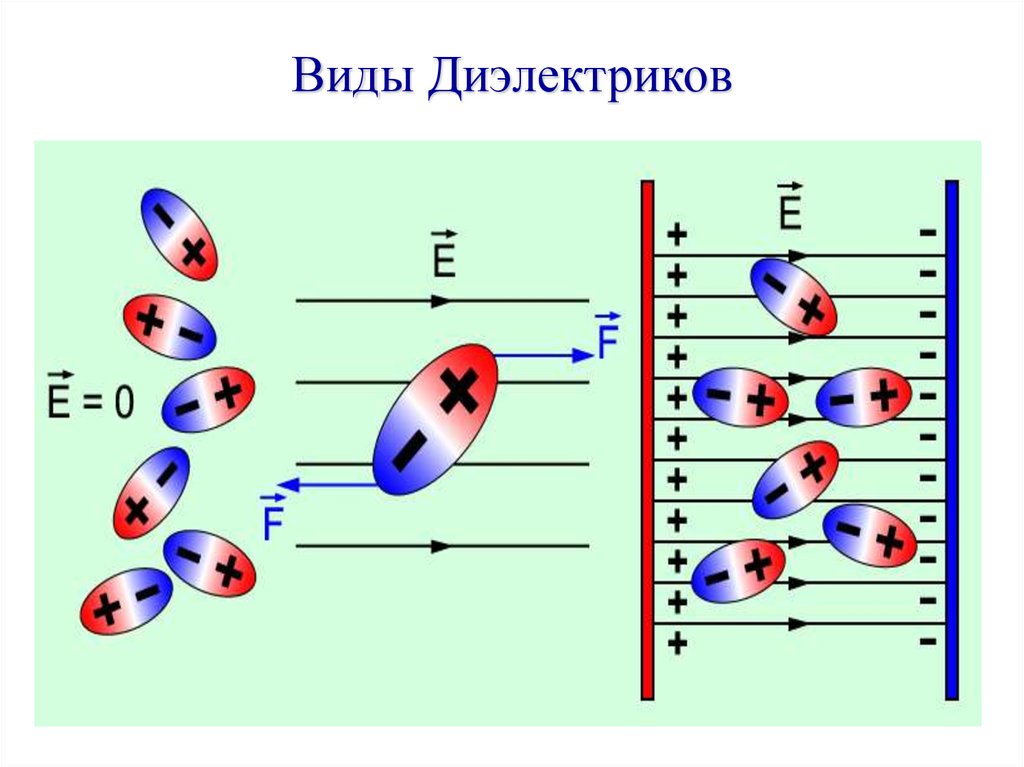
35. Виды Диэлектриков
36.
Электрическое поле в диэлектриках.Типы диэлектриков
Диэлектрики с неполярными молекулами
(H2, N2, O2, CO2)
Молекулы имеют симметричное
строение, т. е. центры «тяжести»
положительных и отрицательных
зарядов в отсутствие внешнего
электрического поля совпадают и
дипольный момент молекулы р
равен нулю.
Под действием внешнего электрического поля заряды неполярных
молекул смещаются в противоположные стороны (положительные
по полю, отрицательные против поля) и молекула приобретает
дипольный момент.
37.
Типы диэлектриковДиэлектрики с полярными молекулами
(H2O, NН3, SO2, CO)
Молекулы
имеют асимметричное
строение, т. е. центры «тяжести»
положительных
и
отрицательных
зарядов не совпадают. В отсутствие
внешнего
электрического
поля
обладают дипольным моментом, но изза теплового движения ориентированы
в пространстве хаотично и их
результирующий момент равен нулю. .
Если такой диэлектрик поместить во внешнее поле, то силы этого
поля будут стремиться повернуть диполи вдоль поля и возникает
отличный от нуля результирующий дипольный момент
38.
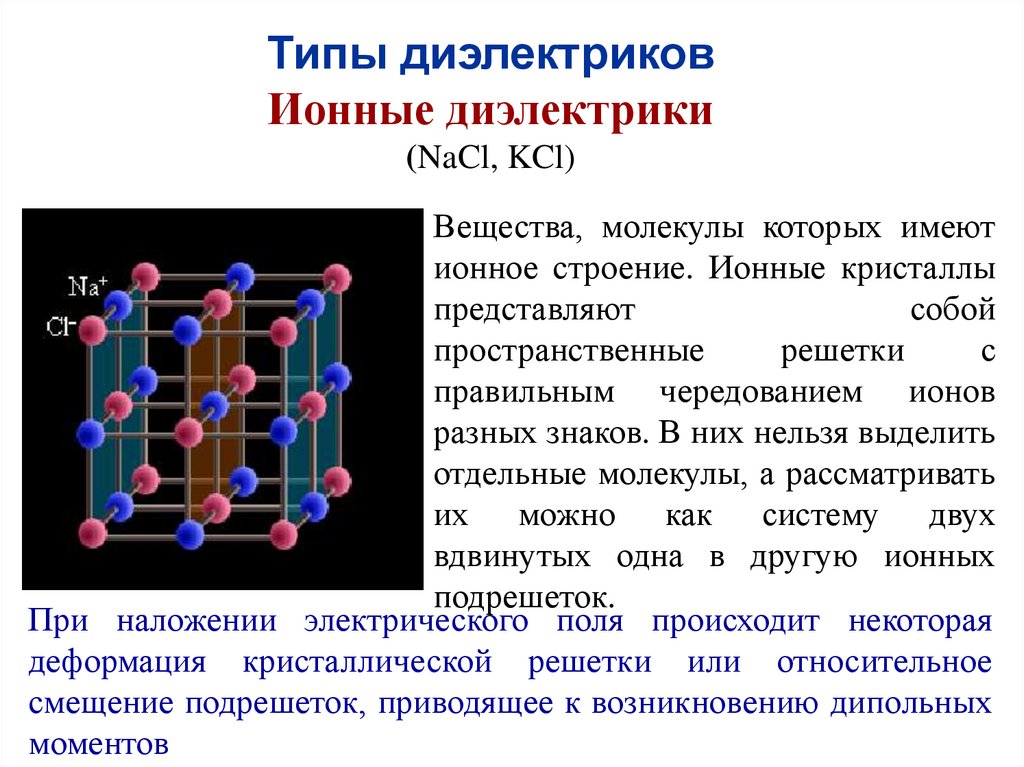
Типы диэлектриковИонные диэлектрики
(NaCl, KCl)
Вещества, молекулы которых имеют
ионное строение. Ионные кристаллы
представляют
собой
пространственные
решетки
с
правильным чередованием ионов
разных знаков. В них нельзя выделить
отдельные молекулы, а рассматривать
их можно как систему двух
вдвинутых одна в другую ионных
подрешеток.
При наложении электрического поля происходит некоторая
деформация кристаллической решетки или относительное
смещение подрешеток, приводящее к возникновению дипольных
моментов
39.
ПоляризованностьПоляризованность – векторная величина, определяемая
дипольным моментом единицы объема диэлектрика
pi
P
V
рi - дипольный момент одной молекулы
Поляризованность для большого
класса диэлектриков линейно
зависит от напряженности поля
P 0 E
- диэлектрическая восприимчивость
https://avatars.mds.yandex.net/get-images-cbir/1513772/zzsbRoN2sqE-6Twf4sZwA4746/ocr
характеризующая свойства диэлектрика
Е′ - поле, создаваемое связанными зарядами,
которое направлено против внешнего поля Е0
40.
Поляризованность'
E E0 E ' E0
0
P ' - повехностная плотность
связанных зарядов
E E0 0 E / 0 E0 E
E0
E0
E
1
1
показывает, во сколько раз поле
ослабляется диэлектриком
характеризует свойство диэлектрика
поляризоваться в электрическом поле.
41.
Электрическое смещение.Теореме Гаусса для поля в диэлектрике
D 0 E
D 0 E (1 ) 0 E 0 E P
Для электрически изотропной среды
D DdS Dn dS
S
S
Поток вектора смещения электростатического
поля в диэлектрике сквозь произвольную
замкнутую поверхность равен алгебраической
сумме заключенных внутри этой поверхности
свободных электрических зарядов
DdS qi
S
i
42.
D 0 En( 1)
n
E dS q
0
n
S
i 1
i
n
EdS q
0
S
i 1
i
43.
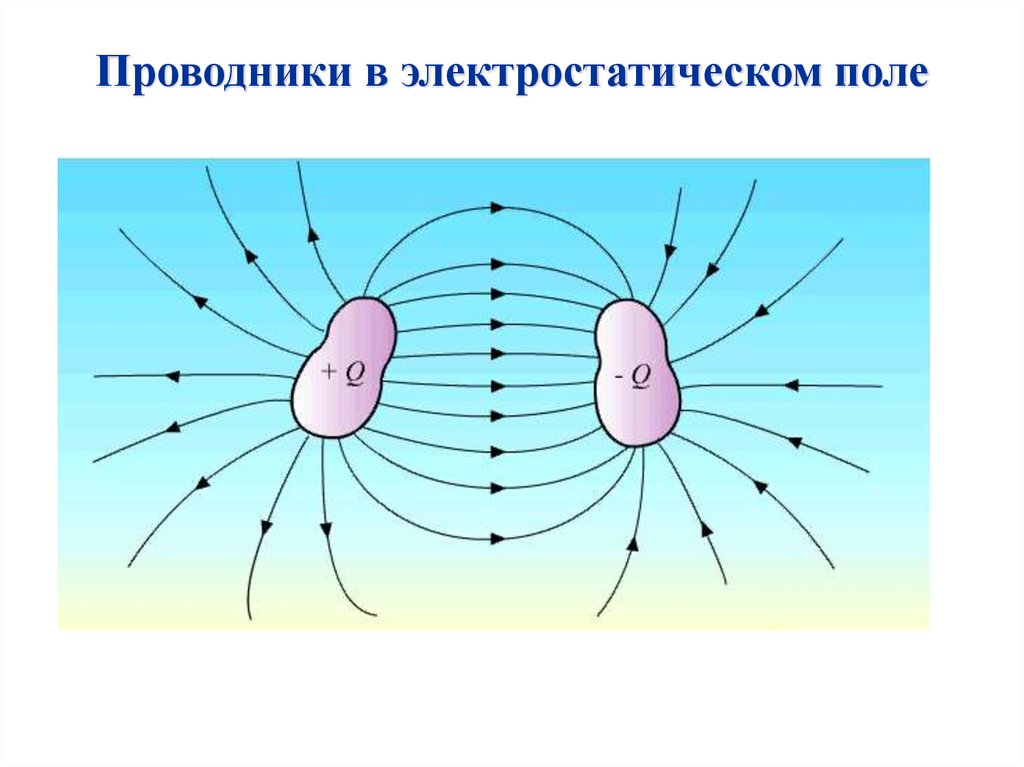
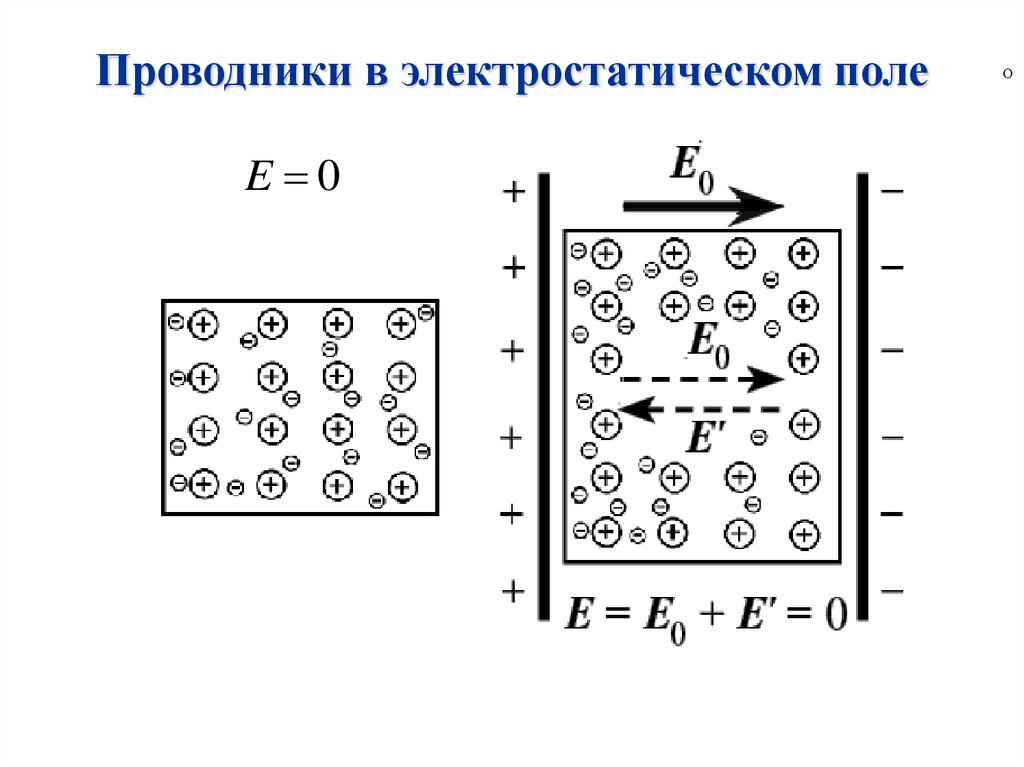
Проводники в электростатическом поле44. Проводники в электростатическом поле
E 0О
45.
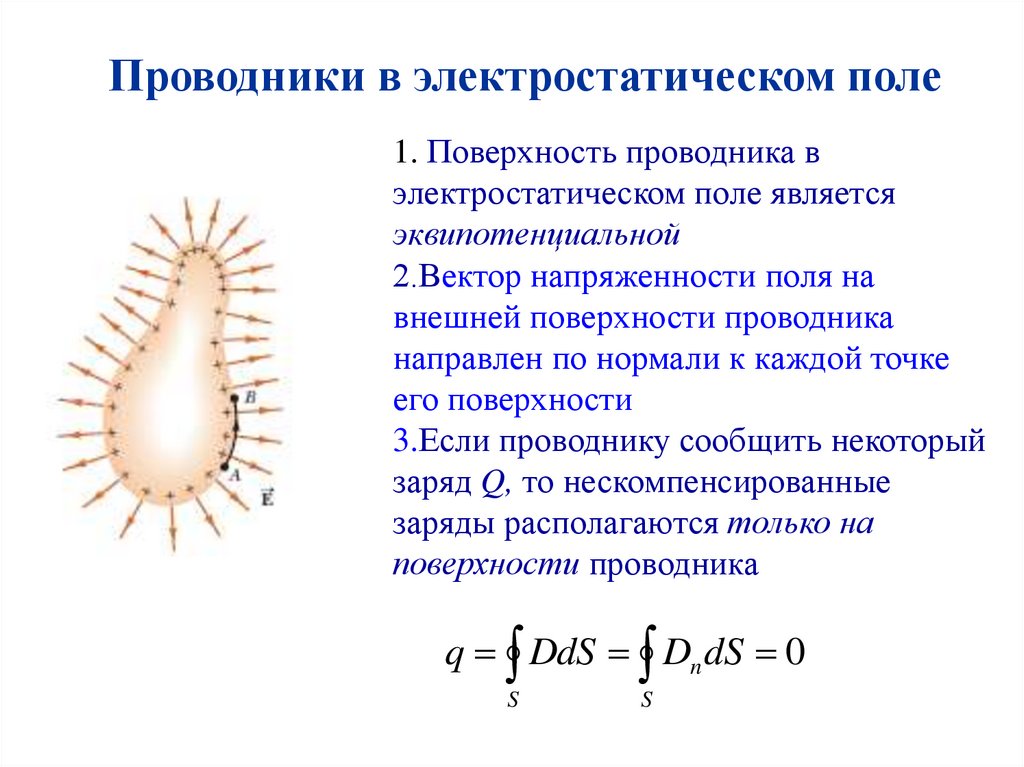
Проводники в электростатическом поле1. Поверхность проводника в
электростатическом поле является
эквипотенциальной
2.Вектор напряженности поля на
внешней поверхности проводника
направлен по нормали к каждой точке
его поверхности
3.Если проводнику сообщить некоторый
заряд Q, то нескомпенсированные
заряды располагаются только на
поверхности проводника
q DdS Dn dS 0
S
S
46.
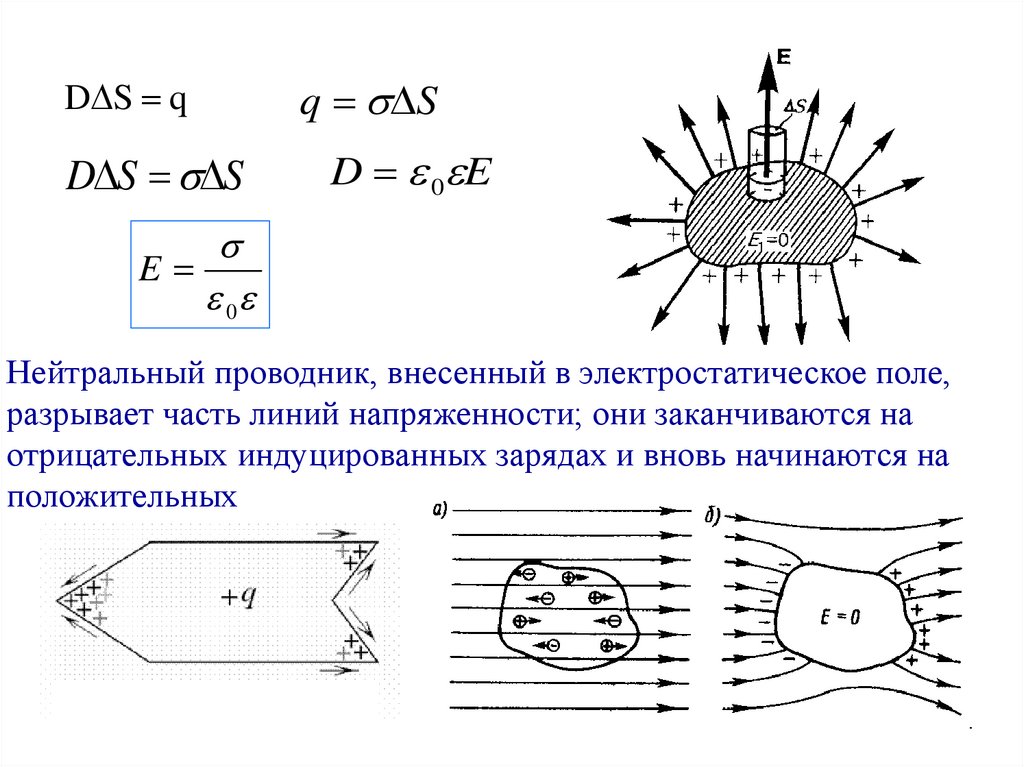
D S qD S S
q S
D 0 E
E
0
Нейтральный проводник, внесенный в электростатическое поле,
разрывает часть линий напряженности; они заканчиваются на
отрицательных индуцированных зарядах и вновь начинаются на
положительных
47.
Электроемкость. Конденсаторы.C
q
48.
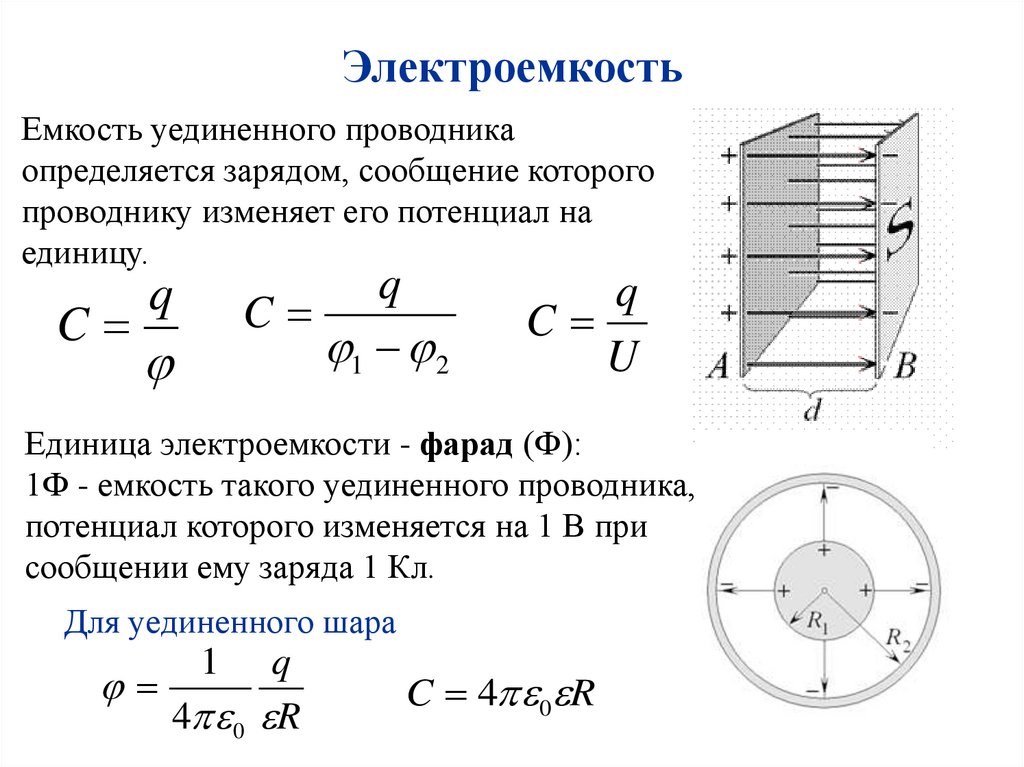
ЭлектроемкостьЕмкость уединенного проводника
определяется зарядом, сообщение которого
проводнику изменяет его потенциал на
единицу.
C
q
C
1 2
q
q
C
U
Единица электроемкости - фарад (Ф):
1Ф - емкость такого уединенного проводника,
потенциал которого изменяется на 1 В при
сообщении ему заряда 1 Кл.
Для уединенного шара
1
q
4 0 R
C 4 0 R
49.
Виды конденсаторови их электроемкости
Плоские
C
0 S
d
Цилиндрические
C
2 0
ln r2 / r1
Сферические
C 4 0
r1r2
r2 r1
Конденсаторы- это устройство для накопления заряда
и энергии электрического поля.
50.
51.
Виды конденсаторов52.
Параллельное соединение:U const
q q1 q2 q3 ... qn
q
C
U
q CU
n
C C1 C 2 ... C n C i
i 1
53.
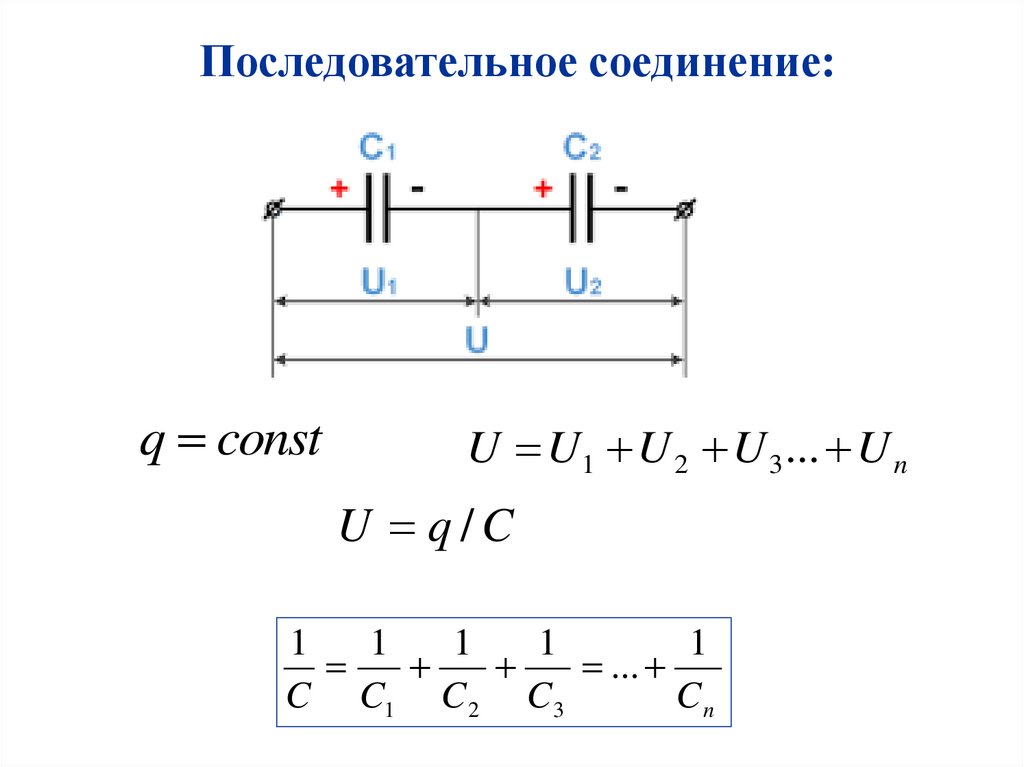
Последовательное соединение:q const
U U1 U 2 U 3 ... U n
U q/C
1
1
1
1
1
...
C C1 C 2 C 3
Cn
54.
Энергия заряженного уединенного проводникаq
q C
W
2C
2
2
2
2
Энергия заряженного конденсатора
q 2 qU CU 2
W
2C
2
2
Механическая (пондеромоторная) сила, с которой
пластины конденсатора притягивают друг друга
2
q2
q2
dW
q
W
x
F
2C 2 0 S
dx
2 0 S
55.
Энергия электростатического поляW
0 E
2
2
Sd
0 E
2
2
V
Объемная плотность энергии
W 0 E
ED
w
V
2
2
2
56.
Кафедра физикиПостоянный ток
57.
План лекции:• 1. Постоянный электрический ток
• 2. Закон Ома для участка цепи.
• 3. ЭДС. Обобщенный закон Ома.
• 4. Дифференцияльная форма законов
Ома и Джоуля-Ленца.
• 5. Правила Кирхгофа.
58. Электрический постоянный ток. Носители электрического тока
• Электрическим током называется упорядоченноедвижение электрических зарядов.
• Носителями тока в проводящей среде являются:
в металлах – свободные электроны
в электролитах – положительные и
отрицательные ионы
в полупроводниках - электроны и положительно
заряженные дырки ,
в газах – ионы обоих знаков и электроны.
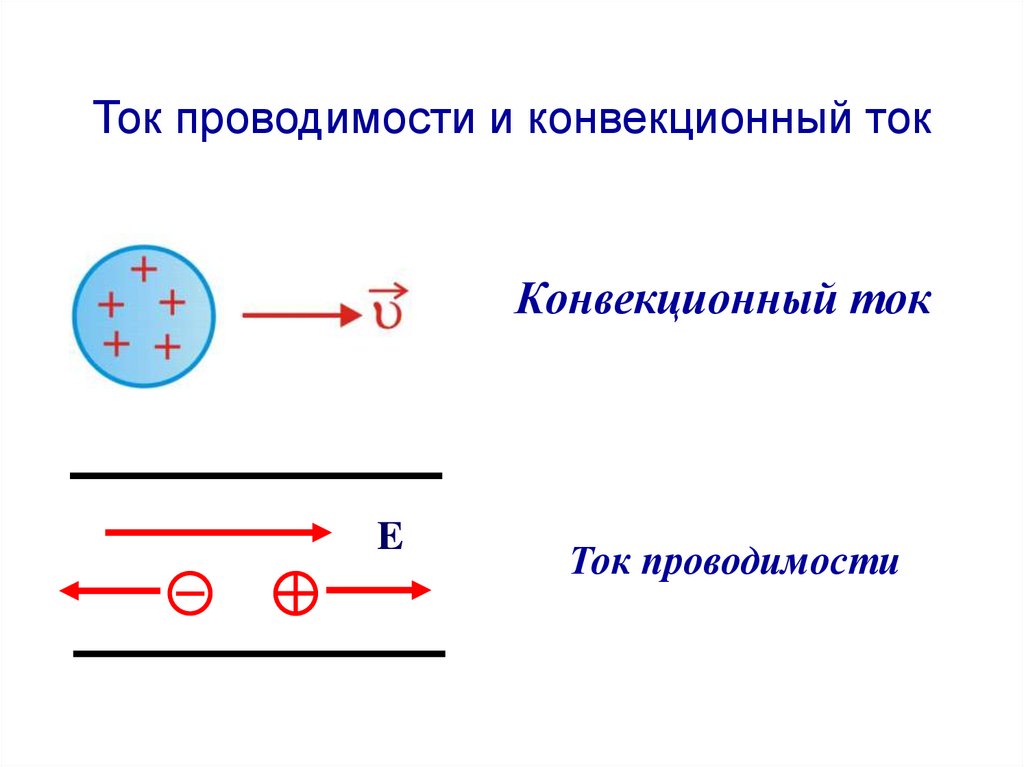
59. Ток проводимости и конвекционный ток
Если в проводнике создать электрическое поле, то в немпод действием поля Е свободные электрические заряды
придут в движение : положительные – по полю,
отрицательные – против поля, то есть в проводнике
возникает ток, называемый током проводимости.
Если в пространстве перемещается заряженное тело, то
ток называется конвекционным
• Таким образом, токи подразделяются на:
– конвекционные (сопровождающиеся переносом
вещества);
– токи проводимости (не сопровождающиеся переносом
вещества)
4
60.
Ток проводимости и конвекционный токКонвекционный ток
E
Ток проводимости
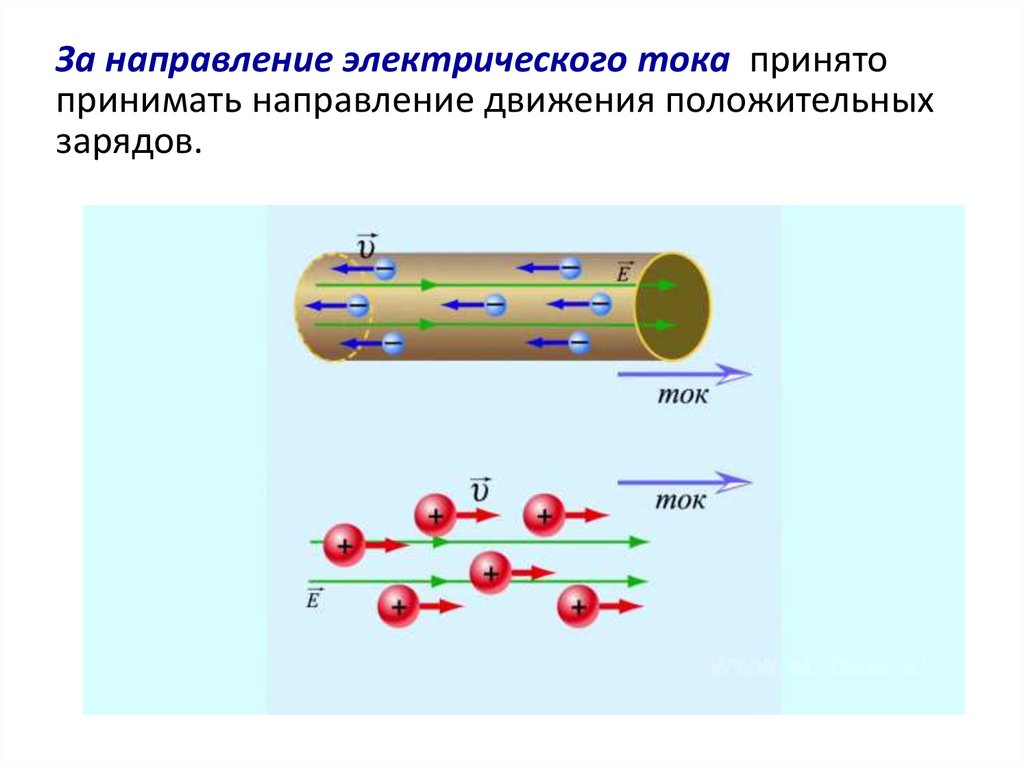
61.
За направление электрического тока принятопринимать направление движения положительных
зарядов.
62. Для возникновения и существования тока необходимо: 1. наличие свободных заряженных частиц; 2. наличие электрического поля в
проводникеОсновной характеристикой, то есть количественной мерой
электрического тока, является сила тока I- скалярная
физическая величина, численно равная заряду,
переносимому через поперечное сечение проводника за
единицу времени:
dq
I
dt
q
I const
t
Если сила тока и его направление не изменяются со
временем, то такой ток называется постоянным.
63. Единица силы тока
• Единицей силы тока является ампер (А)• Один ампер (1 А) – это такая сила тока, которая протекает
по двум прямолинейным параллельным бесконечно
длинным тонким проводникам, расположенным в вакууме
на расстоянии 1 м друг от друга, при которой данные
проводники взаимодействуют с силой 0,2 мкН в расчете на
один метр длины каждого проводника.
• Данная сила взаимодействия имеет магнитную природу.
• Сила тока в 1А соответствует скорости переноса заряда в 1
Кл/с.
64. Плотность тока
Электрический ток может быть распределен по поверхности,через которую он протекает, неравномерно. Поэтому для более
детальной характеристики тока вводят вектор плотности тока j.
Плотность тока – векторная физическая величина
определяемая силой тока через единицу площади поперечного
сечения проводника, перпендикулярного направлению тока:
dI
j
dS
A
м 2
Плотность тока – это вектор, модуль которого равен
отношению силы тока dI через элементарную площадку,
расположенную в данной точке перпендикулярно направлению
движения носителей, к ее площади:
Направление вектора
совпадает с направлением вектора
скорости положительных зарядов.
65.
Найдём силу и плотность тока через скоростьупорядоченного движения зарядов в проводнике.
q neV
d dt
dV Sd S dt
dq ne Sdt
dq
I
ne S
dt
I
j ne
S
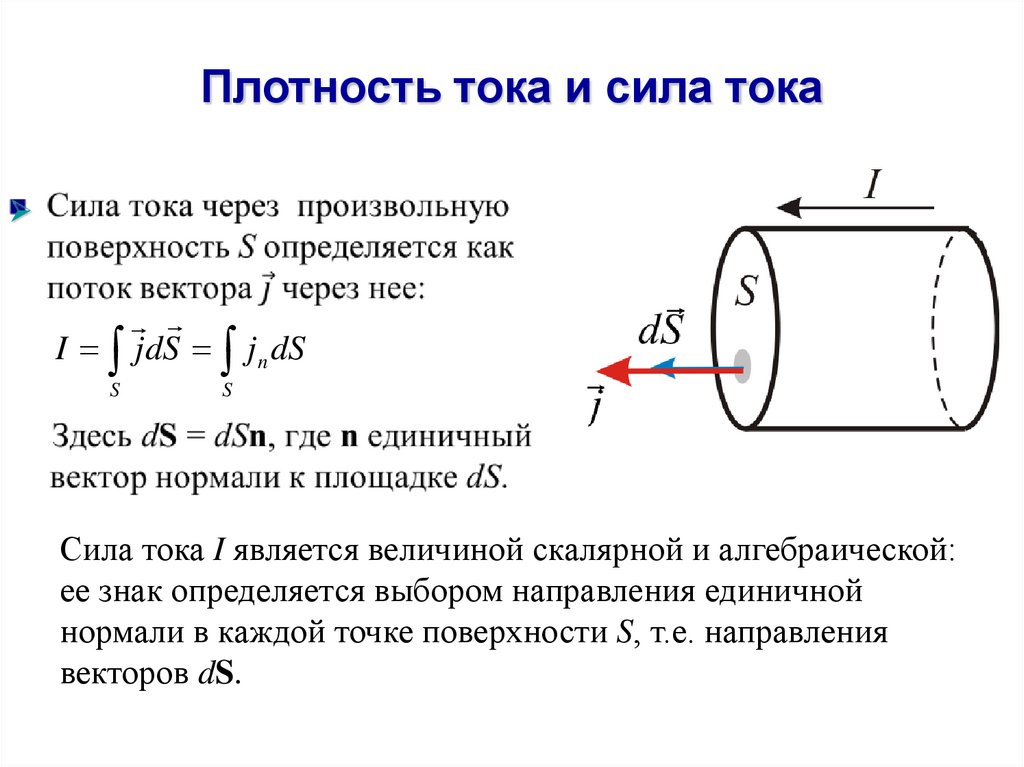
66. Плотность тока и сила тока
I j dS j n dSS
S
Сила тока I является величиной скалярной и алгебраической:
ее знак определяется выбором направления единичной
нормали в каждой точке поверхности S, т.е. направления
векторов dS.
67. Условия возникновения и существования тока
Для возникновения и существования электрического тока вцепи необходимы следующие условия:
наличие свободных носителей тока – заряженных частиц,
способных перемещаться упорядоченно;
наличие электрического поля, энергия которого должна
каким-то образом восполняться.
Если в цепи действуют только силы электростатического поля,
то происходит перемещение положительных носителей от
точек с большим потенциалом к точкам с меньшим
потенциалом. Это привело бы к выравниванию потенциалов,
исчезновению электрического поля и прекращению протекания
электрического тока.
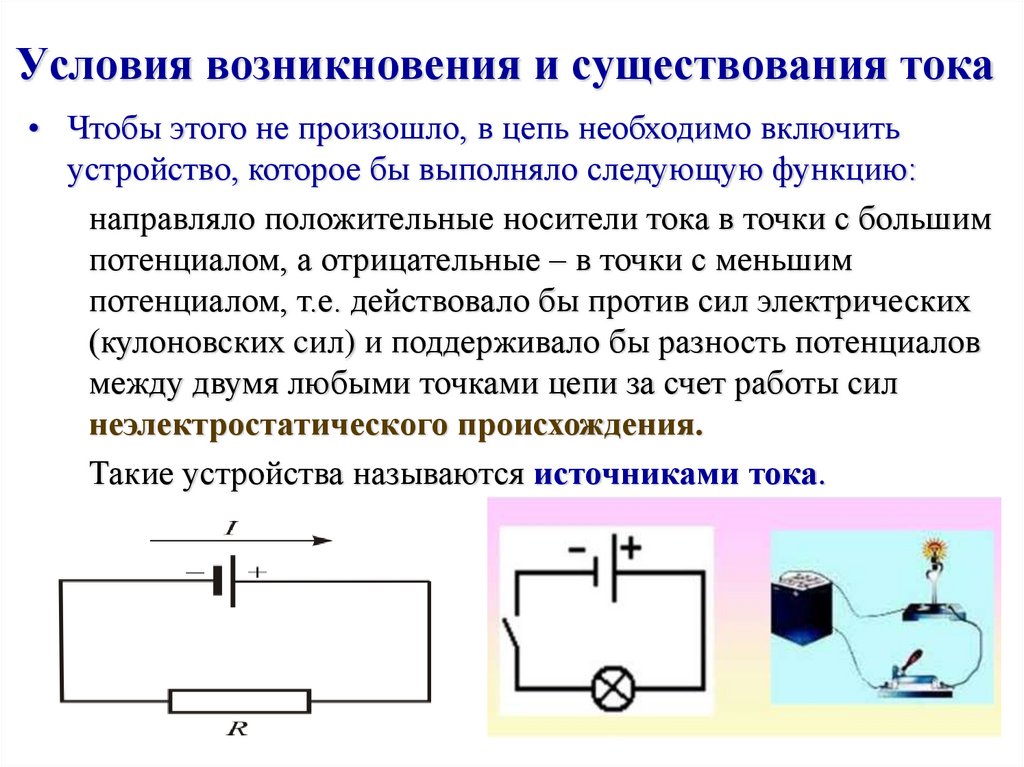
68. Условия возникновения и существования тока
• Чтобы этого не произошло, в цепь необходимо включитьустройство, которое бы выполняло следующую функцию:
направляло положительные носители тока в точки с большим
потенциалом, а отрицательные – в точки с меньшим
потенциалом, т.е. действовало бы против сил электрических
(кулоновских cил) и поддерживало бы разность потенциалов
между двумя любыми точками цепи за счет работы сил
неэлектростатического происхождения.
Такие устройства называются источниками тока.
69. Сторонние силы
Силы не электростатического происхождения,
действующие на заряды со стороны источников тока,
называются сторонними силами.
• Природа сторонних сил: в гальванических элементах они
возникают за счет энергии химических реакций между
электродами и электролитами; в генераторе – за счет
механической энергии вращения ротора генератора;
в солнечных батареях – за счет энергии света (фотонов) и т.п.
Под действием создаваемого поля сторонних сил
электрические заряды движутся внутри источника тока против
сил электрического поля, благодаря чему на концах цепи
поддерживается разность потенциалов и в цепи течет
электрический ток.
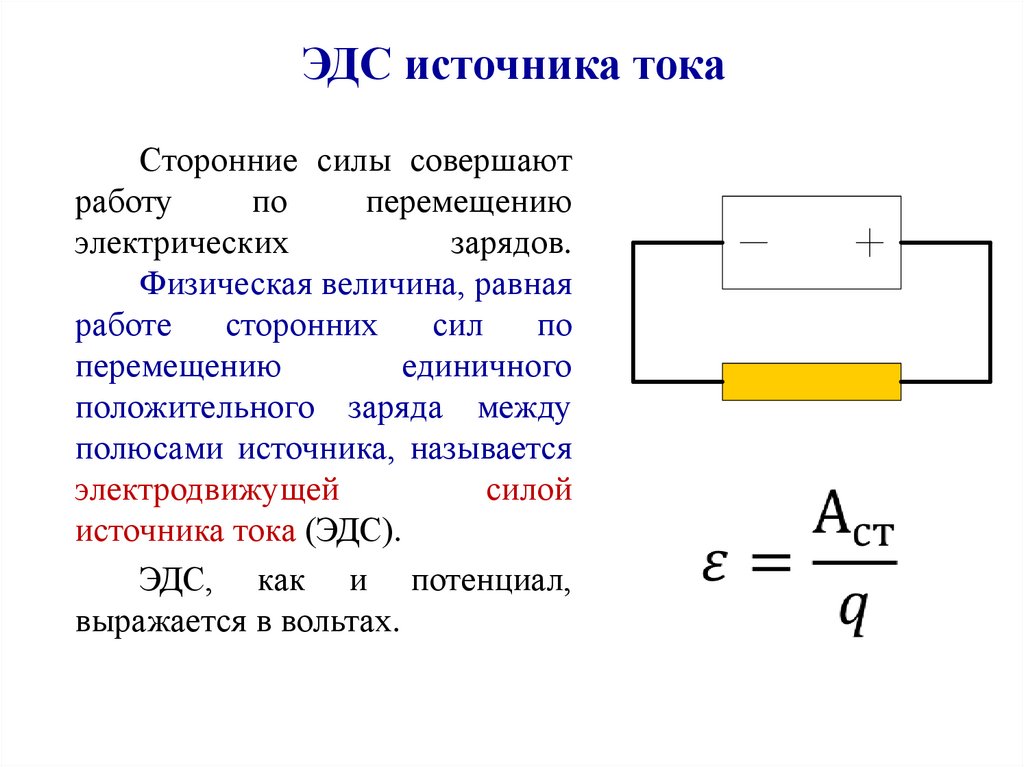
70.
ЭДС источника токаСторонние силы совершают
работу
по
перемещению
электрических
зарядов.
Физическая величина, равная
работе
сторонних
сил
по
перемещению
единичного
положительного заряда между
полюсами источника, называется
электродвижущей
силой
источника тока (ЭДС).
ЭДС, как и потенциал,
выражается в вольтах.
71.
Электродвижущая силаЭДС
А 1 Дж
q 1B
1Кл
U 1 2
72.
Сторонняя сила, действующая на заряд q можетбыть выражена как
Fст qEст
Работа же сторонних сил по перемещению заряда q
на замкнутом участке цепи равна
72
73.
Э.д.с., действующая в замкнутой цепиEст dl
l
то есть Э.д.с., действующая в замкнутой цепи, равна
циркуляции вектора напряженности поля сторонних сил
Э.д.с., действующая на участке цепи 1-2
.
На заряд q помимо сторонних сил действуют также
силы электростатического поля, поэтому
74.
Результирующая сила , действующая в цепи на заряд q иработа этой силы над зарядом q на участке 1-2
F Fэлст Fст q( E Eст )
2
2
A12 Aэлст Aст q Edl q Eст dl
q( 1 2 ) q 12
1
1
Напряжением U на участке 1-2 называется физическая
величина, определяемая работой, совершаемой суммарным
полем электростатических и сторонних сил при перемещении
единичного положительного заряда на данном участке цепи
Aэлст Aст
U12
1 2 12
q
74
75. Закон Ома для однородного участка цепи. Сопротивление проводников
Один из основных законов электродинамикибыл открыт в 1826 г. (опубликован в 1827г)
немецким учителем физики Георгом Омом.
•Сила тока, текущего по однородному
проводнику, прямо пропорциональна
разности потенциалов (напряжению)
на его концах:
1 2 U
I
R
R
Коэффициент пропорциональности 1/R . Величина R называется
электрическим сопротивлением проводника
76. Электрическое сопротивление
• Единица электрического сопротивления – ом (Ом).• 1 Ом – сопротивление такого проводника, при котором при
напряжении 1 В течет постоянный ток силой 1 А.
• Величина G = R-1 называется электрической проводимостью
проводника. Ее единица измерения – сименс (См).
• Сопротивление R проводника зависит от его размеров и
формы, а также от материала, из которого этот проводник
изготовлен.
77. Электрическое сопротивление
• Для однородного линейного проводника длиной l и площадьюпоперечного сечения S сопротивление рассчитывается по
формуле:
l
R
S
• Здесь – удельное электрическое сопротивление –
величина, характеризующая материал проводника. Единица
удельного электрического сопротивления – ом-метр (Ом м).
• Для наиболее хороших проводников при комнатной
температуре составляет ~ 10-8 Ом м.
78.
Вольт-амперная характеристикаI f (U )
79. Закон Ома для однородного участка цепи в дифференциальной форме
1 2 UI
R
R
В векторном виде: 1
j E E
l
R
S
Закон Ома в
дифференциальной форме
- удельная электрическая проводимость вещества
проводника.
Единицей удельной проводимости является сименс на метр (См/м).
80. Зависимость сопротивления проводника от температуры
Опытным путем было установлено,что для большинства случаев
изменение удельного сопротивления
(а значит и сопротивления) с
температурой описывается линейным
законом:
0 1 t R R0 1 t
где и 0, R и R0 – соответственно удельные сопротивления и
сопротивления проводника при температурах t и 0 С (шкала
Цельсия), – температурный коэффициент сопротивления,
[ ] = град-1.
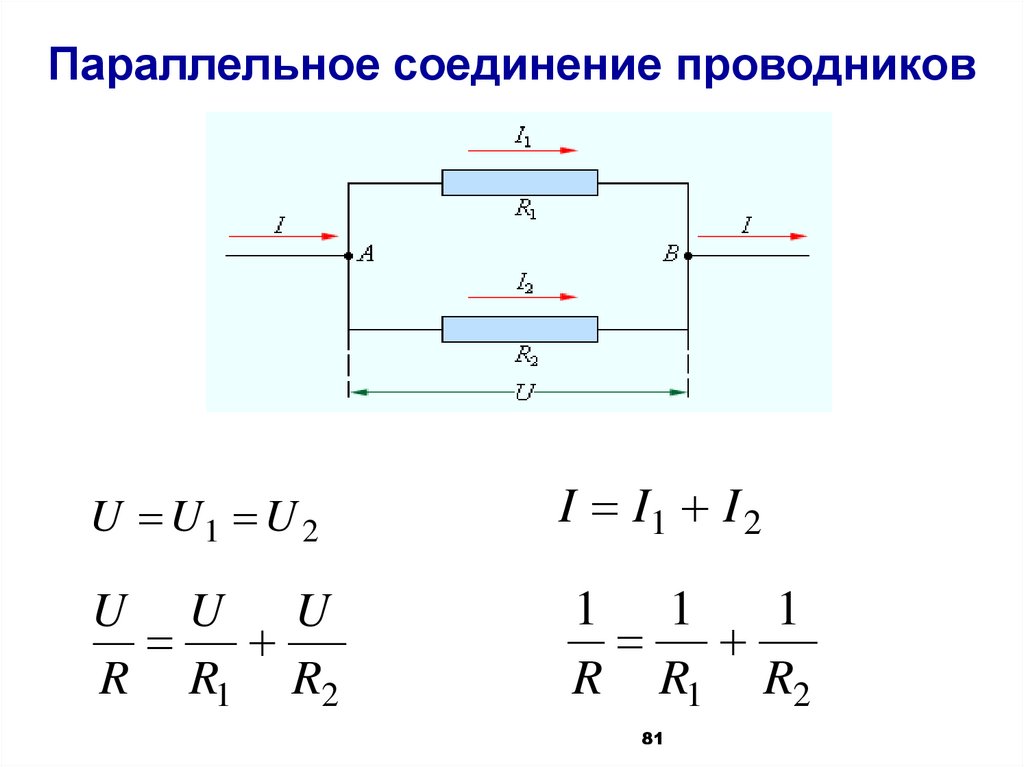
81.
Параллельное соединение проводниковU U1 U 2
I I1 I 2
U U U
R R1 R2
1 1
1
R R1 R2
81
82.
Последовательное соединениепроводников
I1 I 2 I
U U1 U 2
IR IR1 IR2
R R1 R2
82
83.
Закон Ома для неоднородного участка цепиНеоднородный участок цепи - это участок цепи, содержащий
источник ЭДС (т.е. участок, где действуют неэлектрические
силы).
Напряженность
поля в любой точке цепи равна векторной
сумме поля кулоновских сил и поля сторонних сил:
E Eq Eст .
I
1 2
R r
U
R
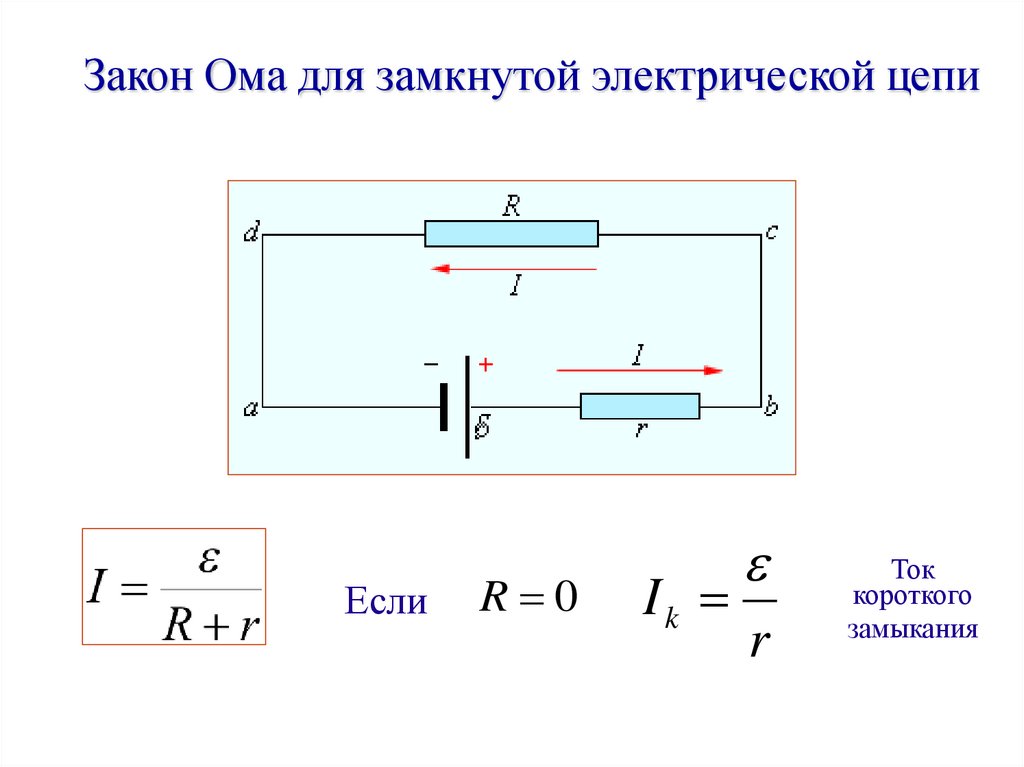
84.
Закон Ома для замкнутой электрической цепиЕсли
R 0
Ik
r
Ток
короткого
замыкания
85.
Работа и мощность токаdq Idt
dA Udq IUdt
U2
A qU IUt
t I 2 Rt
R
A
I U
t
мощность тока
86.
Закон Джоуля - ЛенцаdA dQ
dQ I R dt
2
dQ - если ток идёт по металлическому
проводнику, то вся работа тока идёт на
нагревание проводника
2
U
Q I U t
t
R
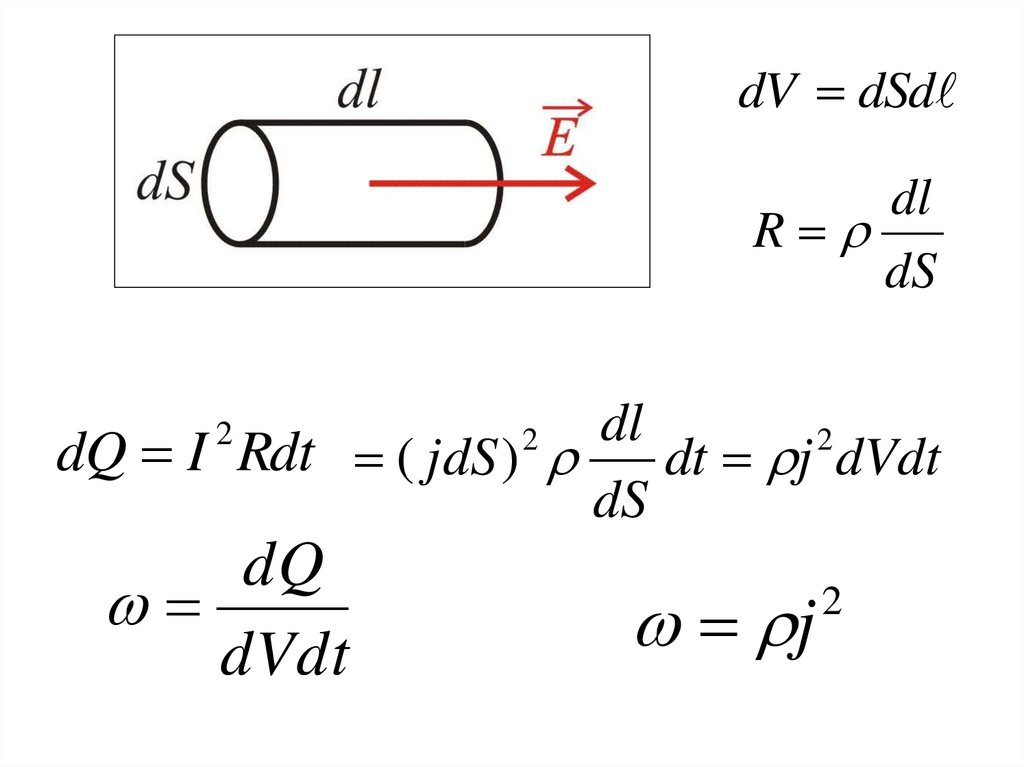
87.
dV dSddl
R
dS
dl
2
dQ I Rdt ( jdS )
dt j dVdt
dS
2
dQ
dVdt
2
j
2
88.
1j E
1
E E
E
2
2
2
2
дифференциальная форма
закона Джоуля-Ленца
89.
Разветвленные цепи. Правила КирхгофаУзлом называется точка, в которой соединяются три или более
проводников.
При этом ток, входящий в узел, считается положительным,
а ток, выходящий из узла, — отрицательным
Участок цепи – отрезок между соседними узлами.
Контур цепи – замкнутая сама на себя последовательность
участков цепи.
Первое правило Кирхгофа.
Алгебраическая сумма токов,
сходящихся в узле, равна нулю.
I1 I 2 I 3 I 4 I 5 0
89
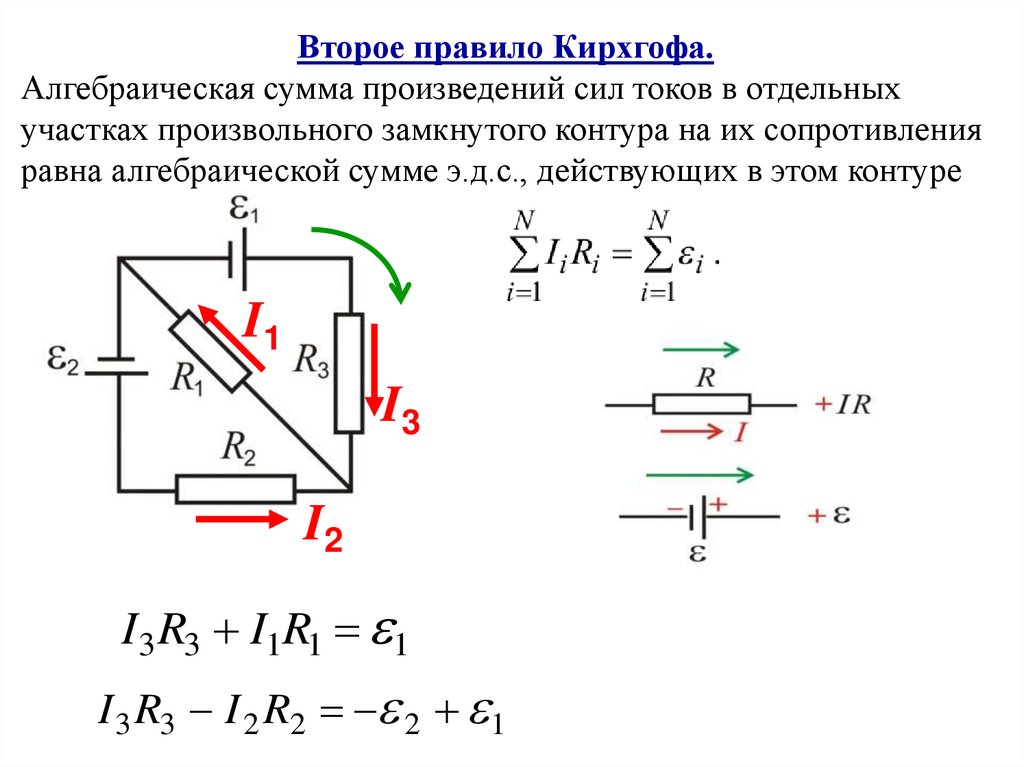
90.
Второе правило Кирхгофа.Алгебраическая сумма произведений сил токов в отдельных
участках произвольного замкнутого контура на их сопротивления
равна алгебраической сумме э.д.с., действующих в этом контуре
I1
I3
I2
I 3 R3 I1R1 1
I 3 R3 I 2 R2 2 1
91.
Второе правило Кирхгофа.Алгебраическая сумма произведений сил токов в отдельных
участках произвольного замкнутого контура на их
сопротивления равна алгебраической сумме э.д.с., действующих
в этом контуре.
Пример.
91
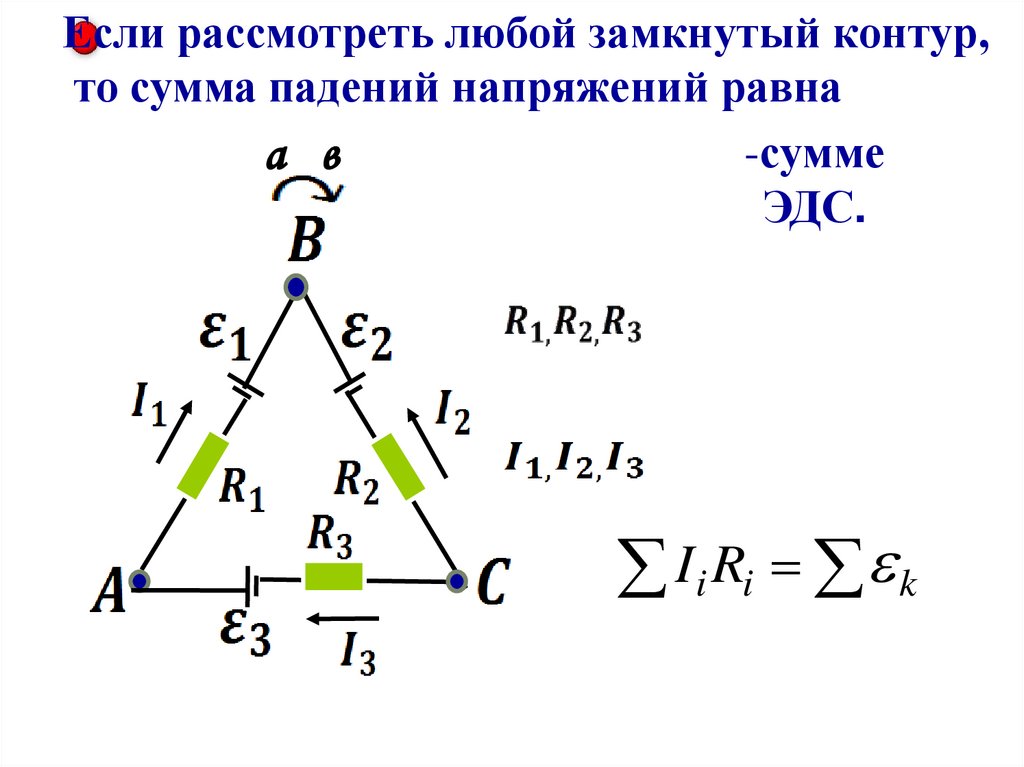
92.
Если рассмотреть любой замкнутый контур,то сумма падений напряжений равна
-сумме
а в
ЭДС.
-
Ii Ri k
93.
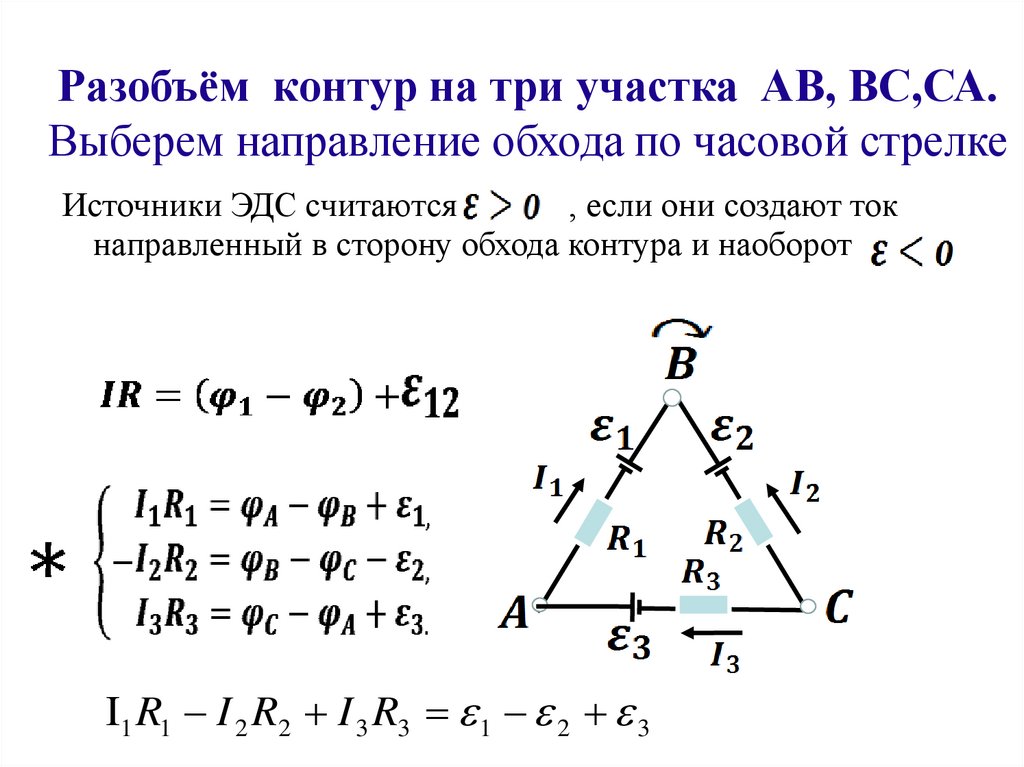
Разобъём контур на три участка АВ, ВС,СА.Выберем направление обхода по часовой стрелке
Источники ЭДС считаются
, если они создают ток
направленный в сторону обхода контура и наоборот .
а в
I1 R1 I 2 R2 I 3 R3 1 2 3






















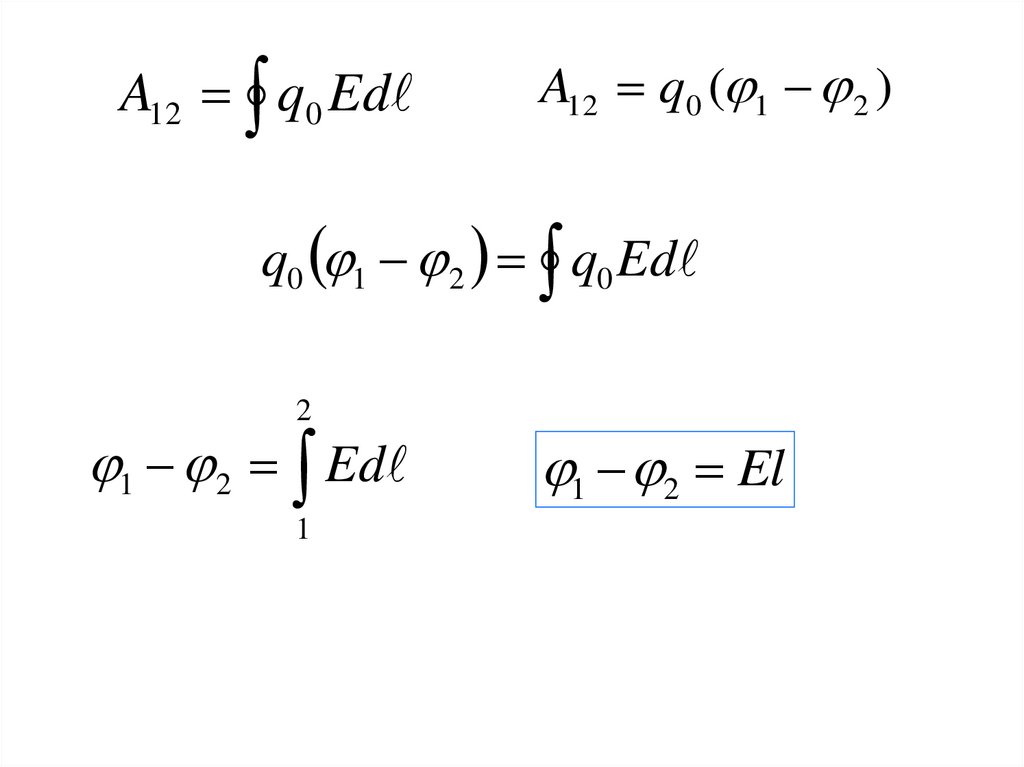








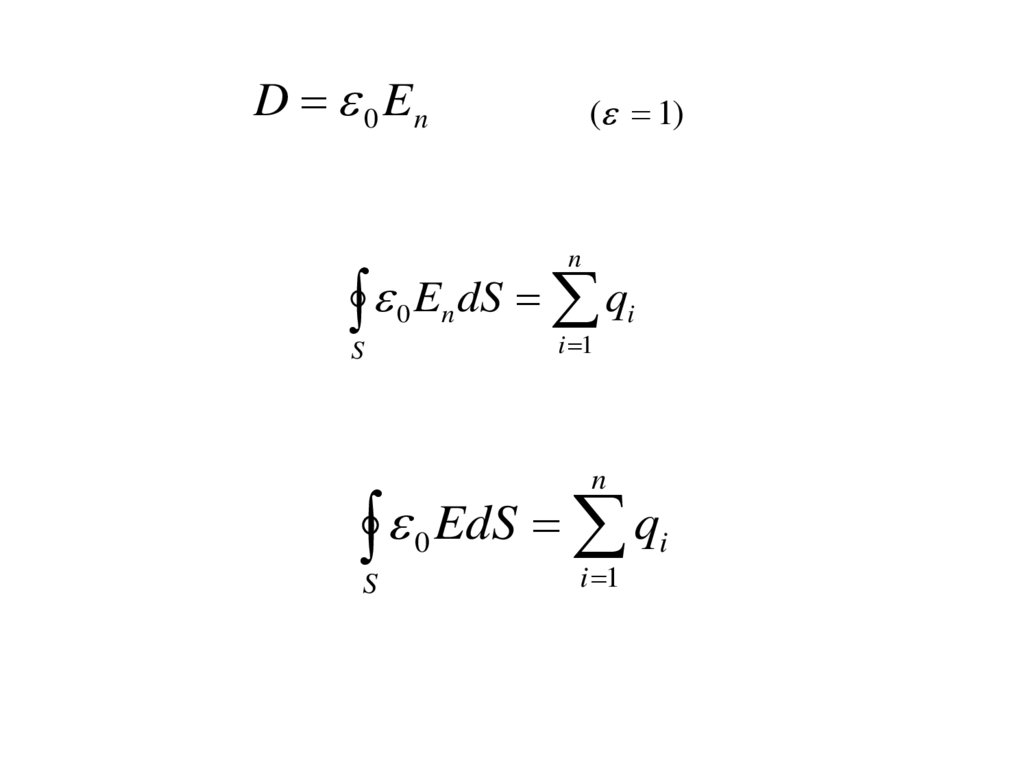


































 physics
physics








