Работа и потенциал электростатического (э/ст) поля. Лекция № 2

1. Лекция № 2

РАБОТА И ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО (э/ст)
ПОЛЯ

2. Работа э/ст поля при перемещении зарядов

В любой точке поля, создаваемого
неподвижным точечным зарядом q на
помещенный в него qпр действует сила
Кулона (центральная сила):
qпр q r
F qпр E
2
4 0 r r
(2.1)
Центральные
силы
–
консервативные, их поле – потенциальное.

3.

Работа центральной силы не зависит
от
траектории,
а
определяется
перемещением qnp (положением т. 1 и т. 2),
т.е. А12= Ã12. Докажем
это:
A F d l
(2.2)
F
F
dl
cos
dr
L
2
dl
1
r1
r
d l cos d r
r2
q
A F d r

4.

r2
qпр q
qпр q (2.3)
A12 F d l F r d r
4
r
4
r
0
1
0
2
L
r
1
W p1
– получено для любой
перемещения заряда.
Wp 2
траектории
Работа консервативных сил
A12= Wp1 - Wp2
(2.4)
Потенциальная энергия заряда qnp в поле
заряда q:
1 q qnp
(2.5)
Wp
4 0 r

5.

Потенциал э/ст поля в данной точке:
Wp qnp
(2.6)
Потенциал
–
энергетическая
характеристика поля; он численно равен
потенциальной энергии, которой обладал
бы в данной точке поля единичный «+»
точечный заряд.
Потенциал точечного заряда q:
1 q
(2.7)
4 0 r
Из (2.6): заряд q, находящийся в
точке поля с потенциалом φ, обладает
потенциальной энергией Wp= qφ.

6.

Работа сил поля над зарядом q:
A12 Wp1 Wp 2 q 1 2
(2.8)
Если заряд q из точки с потенциалом φ
удаляется на бесконечность (φ∞= 0), то
работа:
A q
(2.9)
Потенциал численно равен работе,
которую совершают силы поля над
единичным «+» зарядом при удалении его
из данной точки поля на бесконечность.
В СИ φ= [ 1 B ] (вольт) – такой
потенциал в точке поля, для перемещения
в которую из бесконечности заряда q=1Кл
нужно совершить работу А= 1Дж.

7. Потенциал поля системы точечных зарядов

Работа сил э/ст поля, созданного системой
точечных зарядов {q1,q2,…qi,…qN}, над qпр:
N
A12 Ai12 W p1 Wp 2
i 1
N q q
N q q
1
1
i
np
i
np
4 0 i 1 ri1
4 0 i 1 ri 2
(2.10)
Потенциал э/ст поля системы зарядов:
N q
N
1
i i
(2.11)
4 0 i 1 ri i 1

8.

Поле,
создаваемое
любым
заряженным телом, можно представить как
сумму полей точечных зарядов (принцип
суперпозиции эл. полей). Поэтому любое
э/ст поле потенциально: работа сил э/ст
поля при перемещении в нем qnp не зависит
от траектории движения заряда, а
определяется только его начальным и
конечным положениями.

9.

Рассмотрим в э/ст поле перемещение
qпр по замкнутой траектории
A12
2
1
A A12 A21 (2.12)
A21
A12
2
1
A 12
A21 A12
A A12 A12
(2.13)

10.

В потенциальном (в э/ст) поле
для замкнутого контура
A12 A12
A 0 Т.е.
A qпр E d l qпр El d l 0 (2.14)
L
L
Теорема о циркуляции E
(2.15)
E d l El d l 0
L
L
циркуляция вектора напряженности
э/ст поля по любому замкнутому контуру
равна нулю.

11.

Теорема Стокса:
E d l rot E d S
L
(2.16)
S
Здесь S – поверхность, опирающаяся на
замкнутый контур L,
dS ndS
dS – площадь элементарной поверхности,
n – единичная нормаль к поверхности
в точке выделения ее элемента.

12.

В прямоугольной декартовой
системе
координат ротор или вихрь E
i
j k
rot E E
x y z
Ex E y Ez
Стягивая замкнутый контур L к точке, из
(2.16)
(2.17)
rot E 0
в любой точке э/ст поля.
Э/ст поле – потенциальное,
безвихревое.

13. Связь вектора напряженности и потенциала

Из механики: связь потенциальной
энергии и консервативной силы
F grad Wp Wp
(2.18)
В прямоугольной декартовой сист. к-т
(2.19)
i
j k
x
y
z
В э/ст поле
Из (2.18), (2.20)
F qE , W p q (2.20)
E grad (2.21)

14.

С учетом (2.19)
E i j k , (2.22)
x y z
(2.23)
Ex , E y , E z
z
y
x
Аналогично для проекции E
на
направление силовой линии:
El
l
(2.24)

15. Определение разности потенциалов по заданному полю

E
Приравняем выражение для работы сил
поля по перемещению заряда q из т. 1 в т. 2
выражению (2.8) для той же работы:
2
A12 q E d l q 1 2
1 L
связь разности потенциалов
между рассматриваемыми точками эл.
поля и его напряженности:
2
1 2 E d l (2.25)
1 L

16. Эквипотенциальные поверхности и силовые линии поля

Поверхность,
во
всех
точках
которой
потенциал
φ=const
–
– эквипотенциальная.
Вдоль этой поверхности
dφ = 0 и
E,
составляющая
касательная
к
поверхности
E 0
E (и силовые линии) в каждой точке
поля эквипотенциальной поверхности,
проходящей через данную точку.

17.

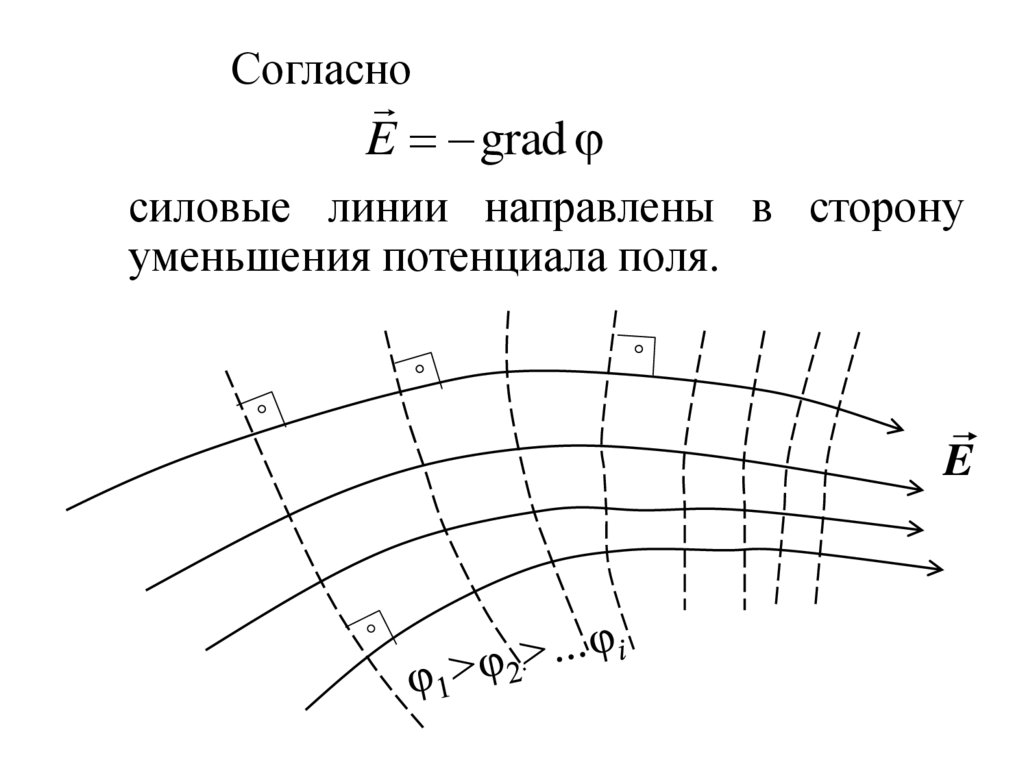
Согласно
E grad
силовые линии направлены в сторону
уменьшения потенциала поля.
E

18. Уравнение Пуассона

Э/ст поле можно описать, задавая M
Основная задача э/статики: зная
распределение эл. зарядов, заданное в
каждой точке пространства объемной
плотностью заряда ρ = ρ(M), определить
соответствующее
распределение
потенциала э/ст поля в вакууме. Из (1.2.12):
и (2.21): E grad
div E 0
получаем уравнение Пуассона
M
2
div grad
0
(2.26)

19.

Решение основной задачи э/статики
сводится к решению ДУ (2.26).
Однородное уравнение (2.26) при ρ = 0 –
– уравнение Лапласа:
0
(2.27)
Теорема единственности
Определение потенциала сводится к
нахождению такой функции φ(r), которая
удовлетворяет либо уравнению Пуассона,
либо уравнению Лапласа, с учетом ГУ.
Эта задача имеет единственное решение.