Линейная функция, ее график и свойства

1.

2.

Актуализация знаний
Функцией
называется зависимость одной переменной
от другой, при которой одному значению независимой
переменной
соответствует
единственное
значение
зависимой переменной.
Область определения функции
все значения,
которые может принимать независимая переменная - Х –
аргумент, абсцисса точки
Область значений функции - все значения, которые
может принимать зависимая переменная – У – функция,
ордината точки
-
Графиком функции называется множество всех точек
координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты- соответствующим
значениям функции.

3.

4.

Задача 1.
Мама купила несколько конфет по цене 5 рублей
за конфету и одну шоколадку по цене 65 рублей.
Сколько она заплатила за всю покупку?
Составьте выражение, с помощью которого
можно подсчитать стоимость покупки.
n - рублей стоит вся покупка
d – количество конфет
Как вы думаете, от чего зависит стоимость
покупки?
n=5d+65
От числа покупаемых конфет.

5. Итак, мы получили формулу: n = 5d + 65

Общий вид формулы:
y = kx + b, где k и b –
некоторые числа, x – переменная величина.
Функция, с которой мы столкнулись в данной задаче,
называется линейной.

6.

Функция вида y = kx + b – называется
линейной функцией, где
х – аргумент (независимая переменная),
у – функция (зависимая переменная),
k, b – некоторые числа (коэффициенты),
k≠0

7.

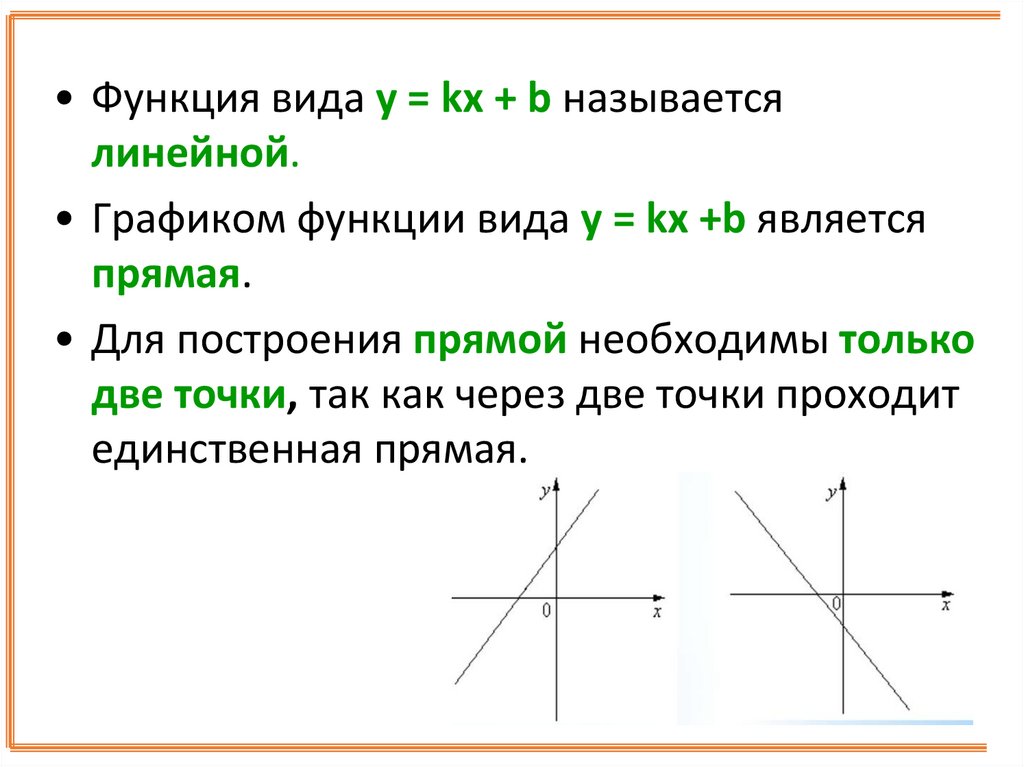
• Функция вида у = kx + b называется
линейной.
• Графиком функции вида у = kx +b является
прямая.
• Для построения прямой необходимы только
две точки, так как через две точки проходит
единственная прямая.

8.

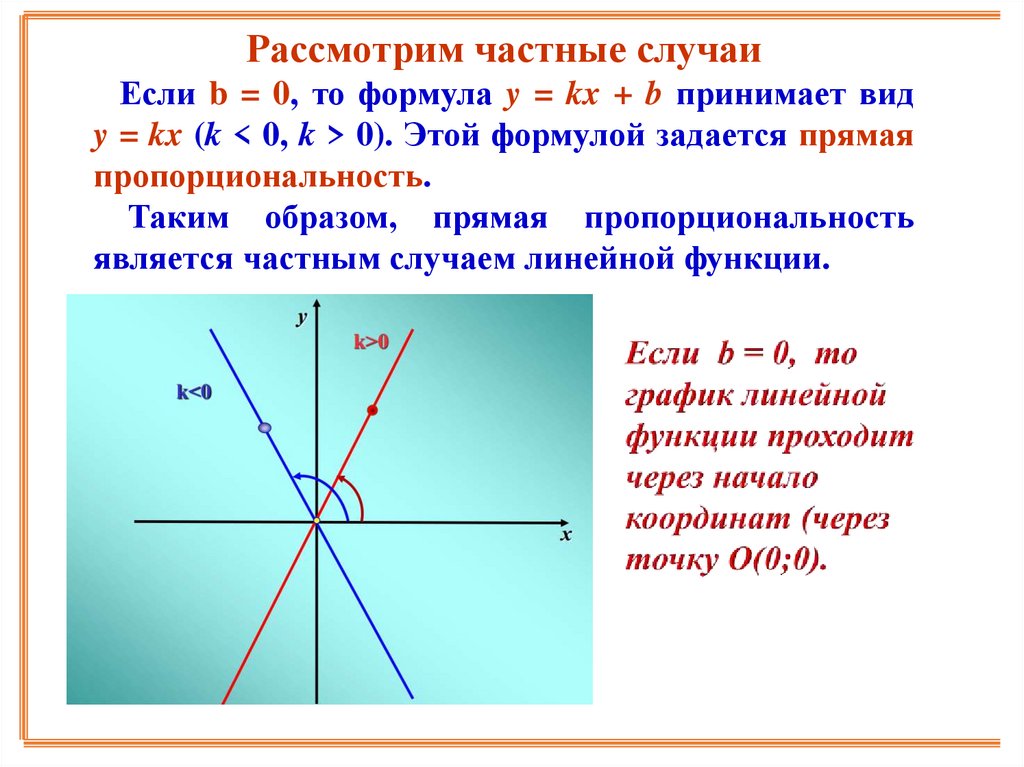
Рассмотрим частные случаи
Если b = 0, то формула y = kx + b принимает вид
y = kx (k < 0, k > 0). Этой формулой задается прямая
пропорциональность.
Таким образом, прямая пропорциональность
является частным случаем линейной функции.

9.

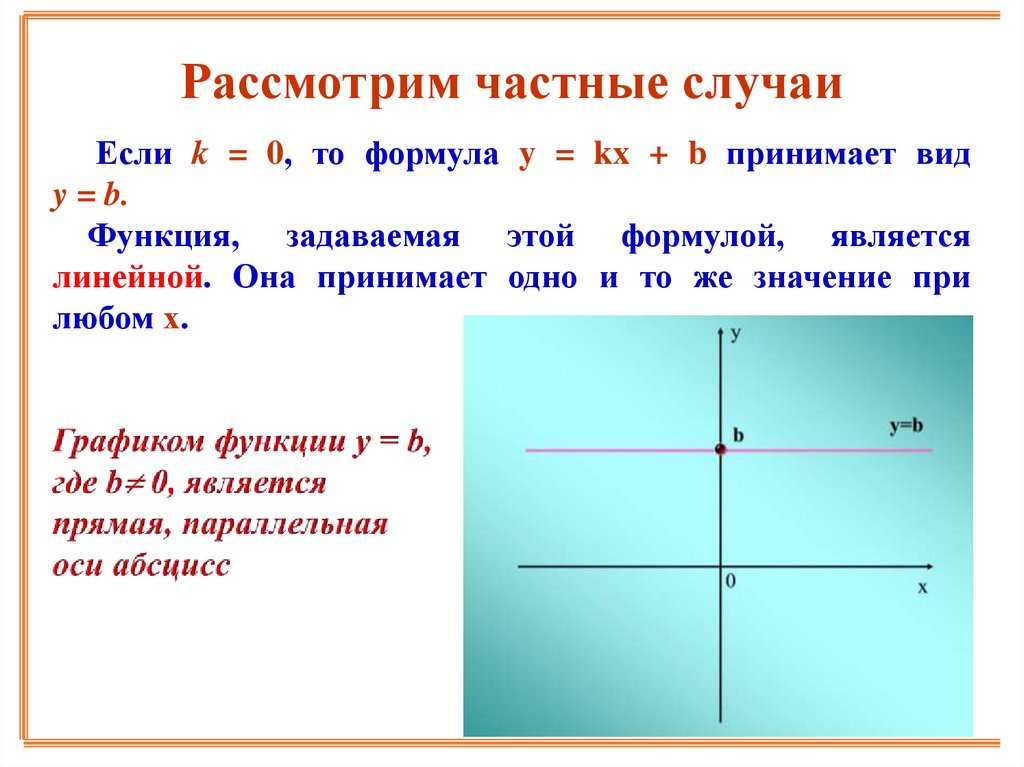
Рассмотрим частные случаи
Если k = 0, то формула y = kx + b принимает вид
y = b.
Функция, задаваемая этой формулой, является
линейной. Она принимает одно и то же значение при
любом х.

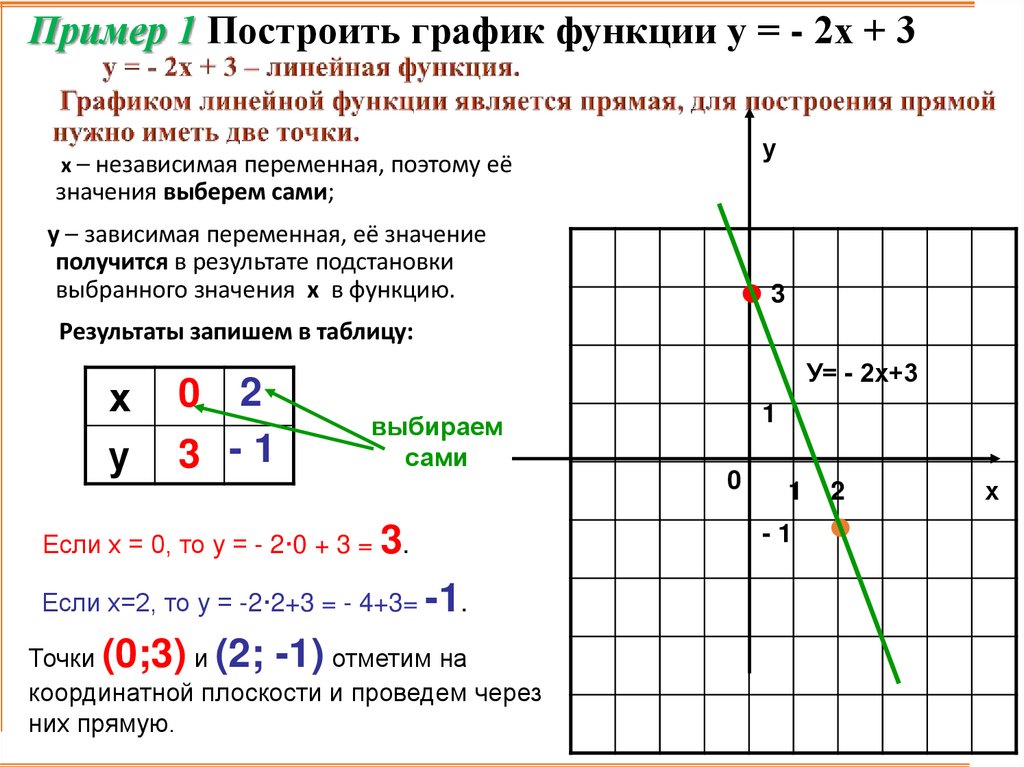
10. у = - 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки.

Пример 1 Построить график функции у = - 2х + 3
у
х – независимая переменная, поэтому её
значения выберем сами;
у – зависимая переменная, её значение
получится в результате подстановки
выбранного значения х в функцию.
3
Результаты запишем в таблицу:
х
у
0 2
3 -1
У= - 2х+3
выбираем
сами
Если х = 0, то у = - 2·0 + 3 = 3.
Если х=2, то у = -2·2+3 = - 4+3= -1.
Точки (0;3) и (2; -1) отметим на
координатной плоскости и проведем через
них прямую.
1
0
1
-1
2
х

11.

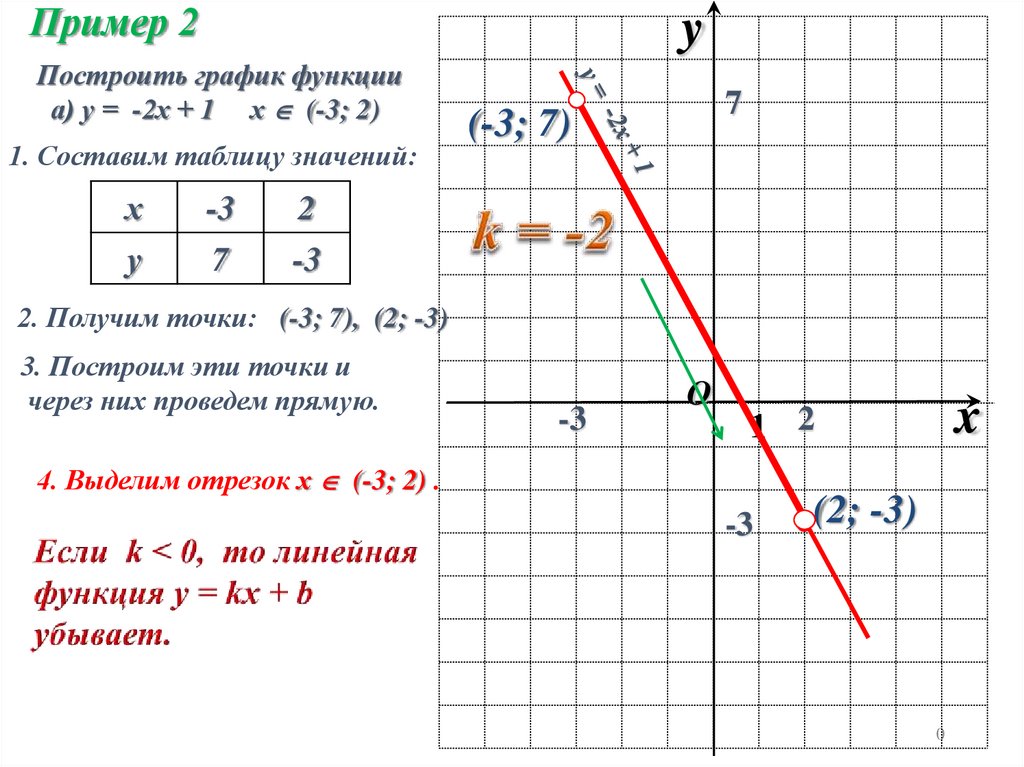
Пример 2
y
Построить график функции
а) у = -2х + 1 х (-3; 2)
1. Составим таблицу значений:
х
-3
2
у
7
-3
7
(-3; 7)
2. Получим точки: (-3; 7), (2; -3)
3. Построим эти точки и
через них проведем прямую.
-3
O
4. Выделим отрезок х (-3; 2) .
-3
10.10.2015
График функции
x
1 2
(2; -3)
0

12.

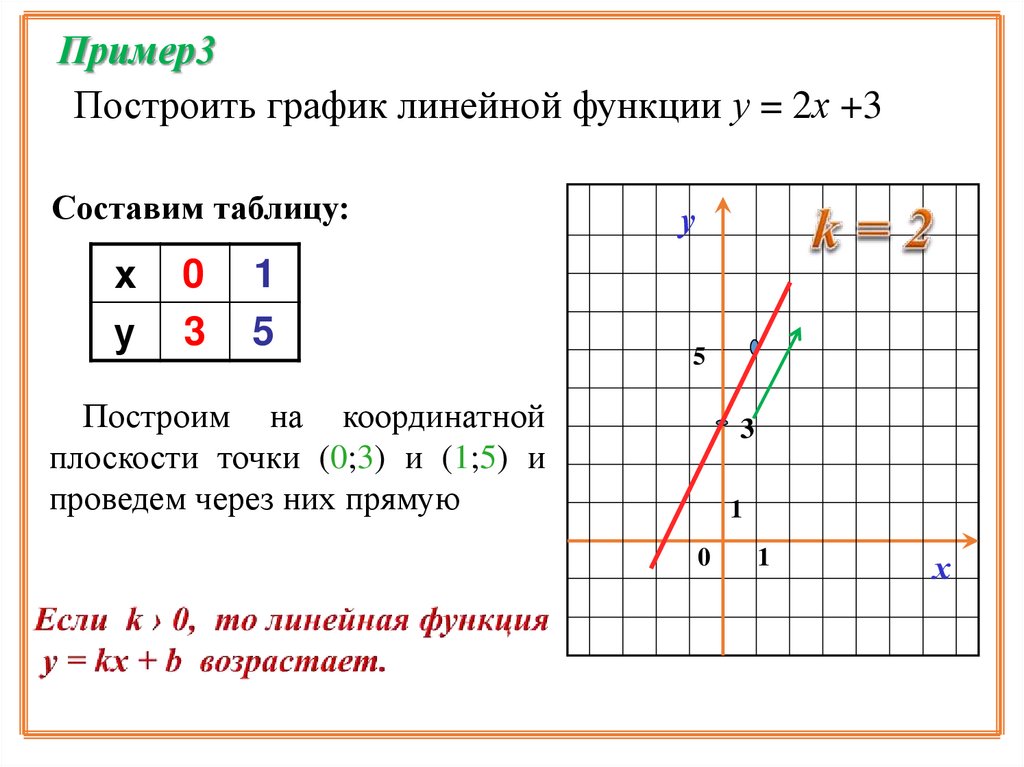
Пример3
Построить график линейной функции у = 2х +3
Составим таблицу:
х
у
0
3
1
5
у
5
Построим на координатной
плоскости точки (0;3) и (1;5) и
проведем через них прямую
3
1
0
1
х

13.

Функция у = kx + b называется возрастающей, если
большему значению аргумента соответствует
большее значение функции (двигаясь по графику
функции, мы поднимаемся вверх).
Функция у = kx + b называется убывающей, если
большему значению аргумента соответствует
меньшее значение функции (двигаясь по графику
функции, мы опускаемся вниз).
10.10.2015
График линейной функции

14.

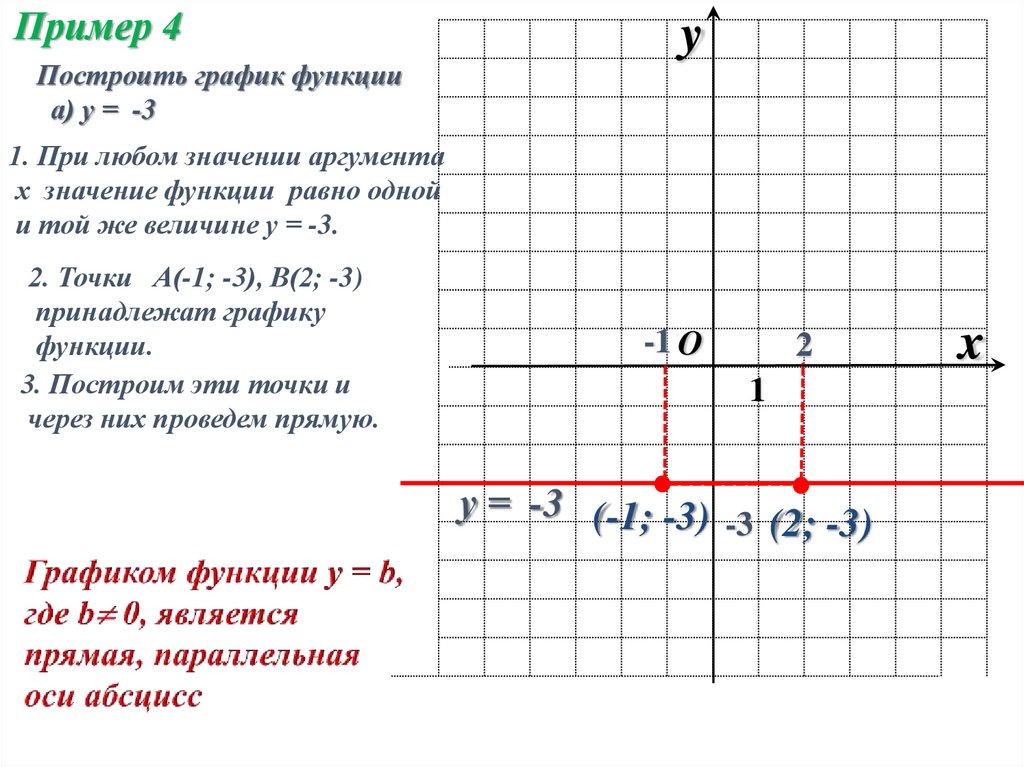
Пример 4
Построить график функции
а) у = -3
y
1. При любом значении аргумента
х значение функции равно одной
и той же величине у = -3.
2. Точки А(-1; -3), В(2; -3)
принадлежат графику
функции.
3. Построим эти точки и
через них проведем прямую.
-1 O
2
1
у = -3 (-1; -3) -3 (2; -3)
x

15.

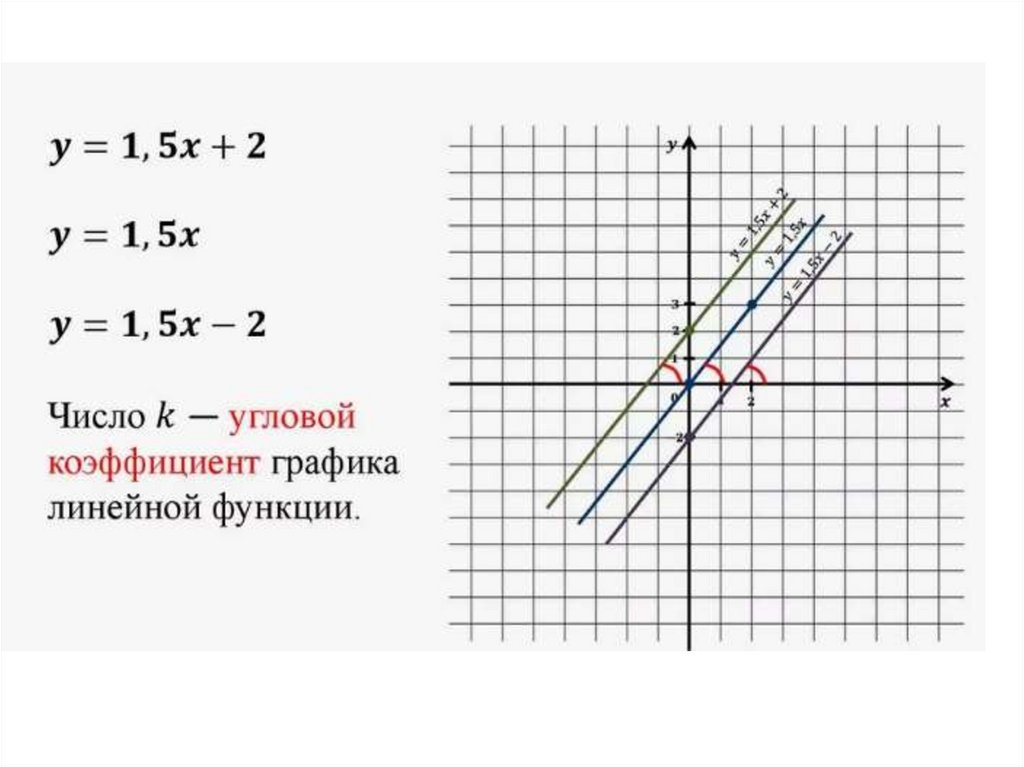
Величина k определяет наклон графика
функции y = kx + b
10.10.2015
График линейной функции

16.

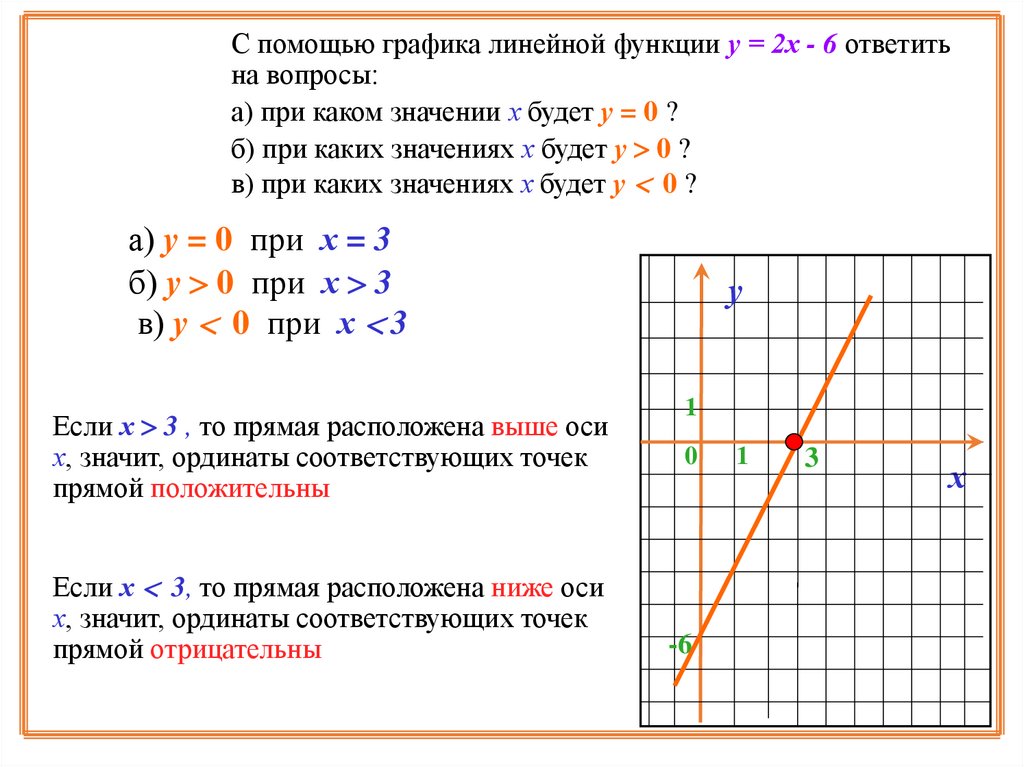
С помощью графика линейной функции у = 2х - 6 ответить
на вопросы:
а) при каком значении х будет у = 0 ?
б) при каких значениях х будет у 0 ?
в) при каких значениях х будет у 0 ?
а) у = 0 при х = 3
б) у 0 при х 3
в) у 0 при х 3
Если х 3 , то прямая расположена выше оси
х, значит, ординаты соответствующих точек
прямой положительны
Если х 3, то прямая расположена ниже оси
х, значит, ординаты соответствующих точек
прямой отрицательны
у
1
0
-6
1
3
х