Изгиб прямого бруса. Тема 2.6

1. Тема 2.6 ИЗГИБ ПРЯМОГО БРУСА

Сопротивление материалов
Тема 2.6
ИЗГИБ ПРЯМОГО БРУСА
1. Общие сведения об изгибе
2. Классификация видов изгиба
3. Внутренние силовые факторы при изгибе
Преподаватель технической механики – Шепелева Е.В.

2.

Вопросы
1. Общие сведения об изгибе
2. Классификация видов изгиба
3. Внутренние силовые факторы при изгибе

3.

Общие сведения об изгибе
Элементы конструкций работающих на
изгиб, называют балками.
Изгибом
называется
такой
вид
деформации, при котором в поперечном
сечении
возникает
один
внутренний
силовой фактор изгибающий момент
(чистый изгиб), или два внутренних
силовых фактора изгибающий момент и
поперечная сила ( поперечный изгиб).

4.

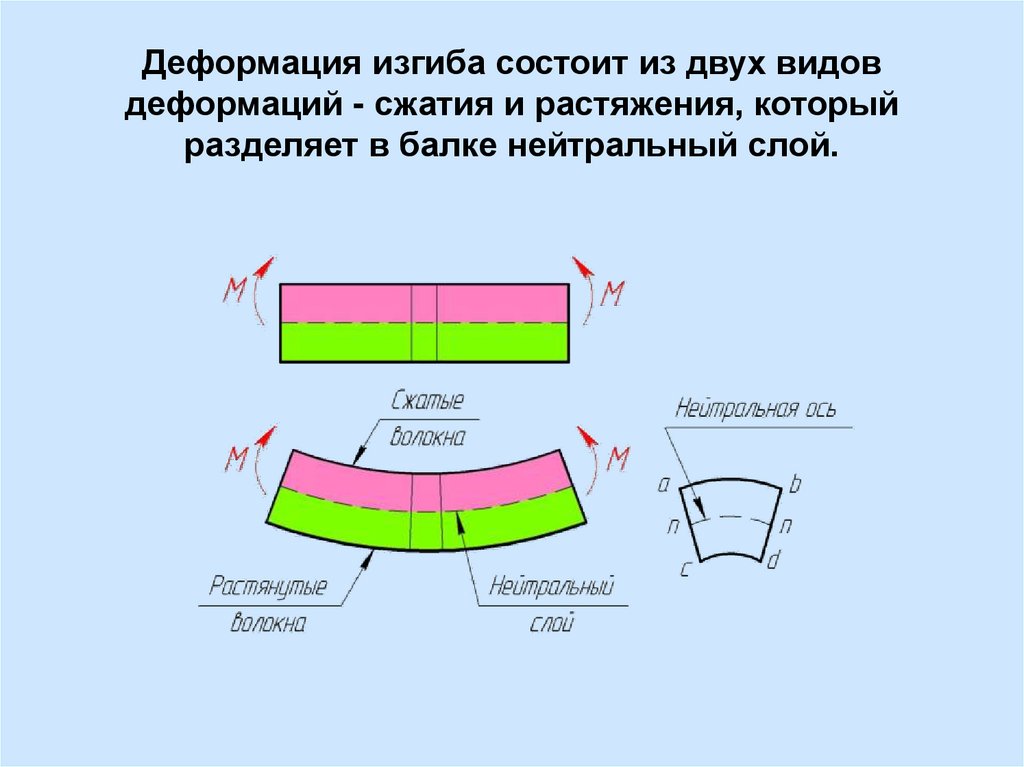
Деформация изгиба состоит из двух видов
деформаций - сжатия и растяжения, который
разделяет в балке нейтральный слой.

5.

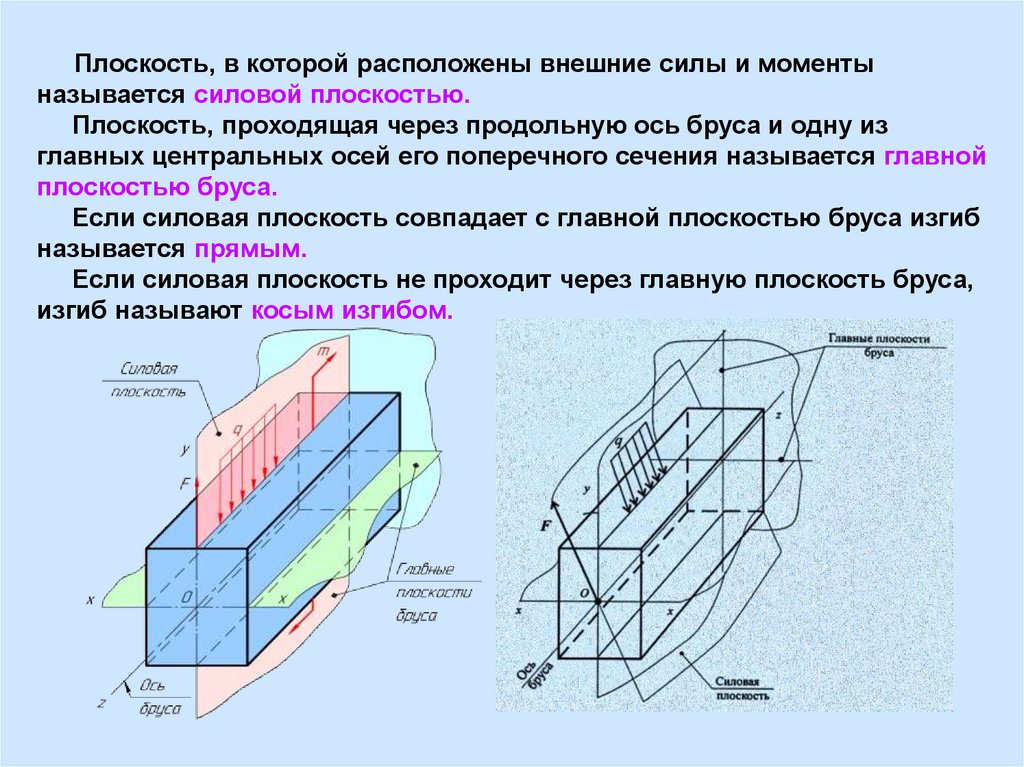
Плоскость, в которой расположены внешние силы и моменты
называется силовой плоскостью.
Плоскость, проходящая через продольную ось бруса и одну из
главных центральных осей его поперечного сечения называется главной
плоскостью бруса.
Если силовая плоскость совпадает с главной плоскостью бруса изгиб
называется прямым.
Если силовая плоскость не проходит через главную плоскость бруса,
изгиб называют косым изгибом.

6.

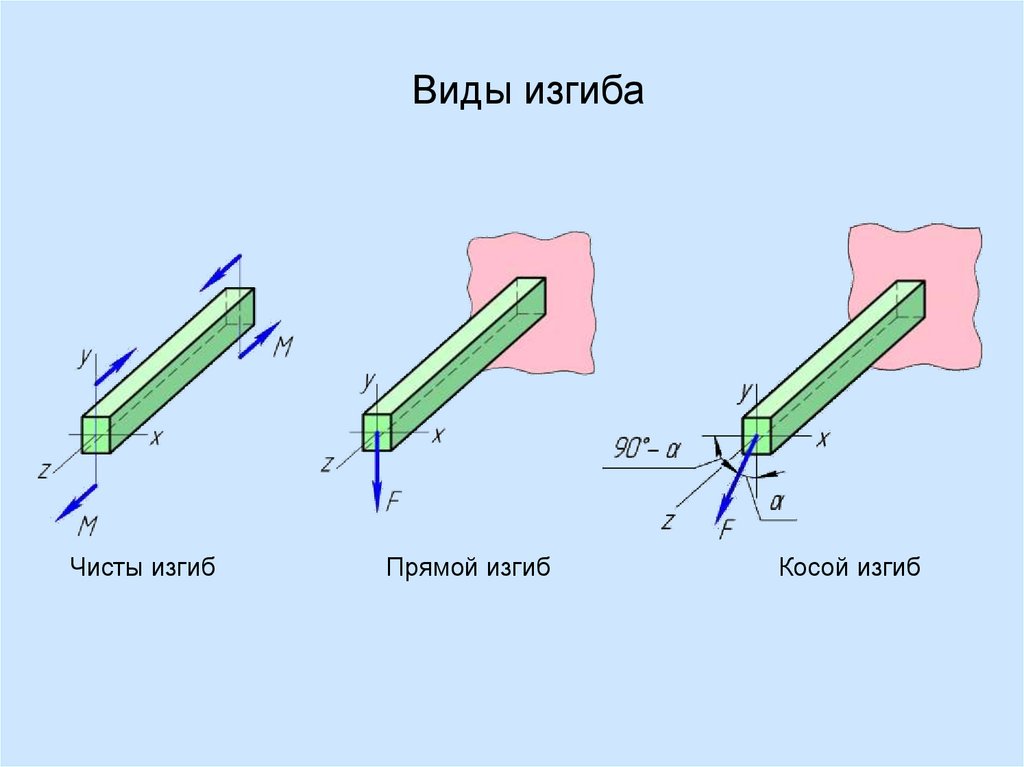
Виды изгиба
Чисты изгиб
Прямой изгиб
Косой изгиб

7.

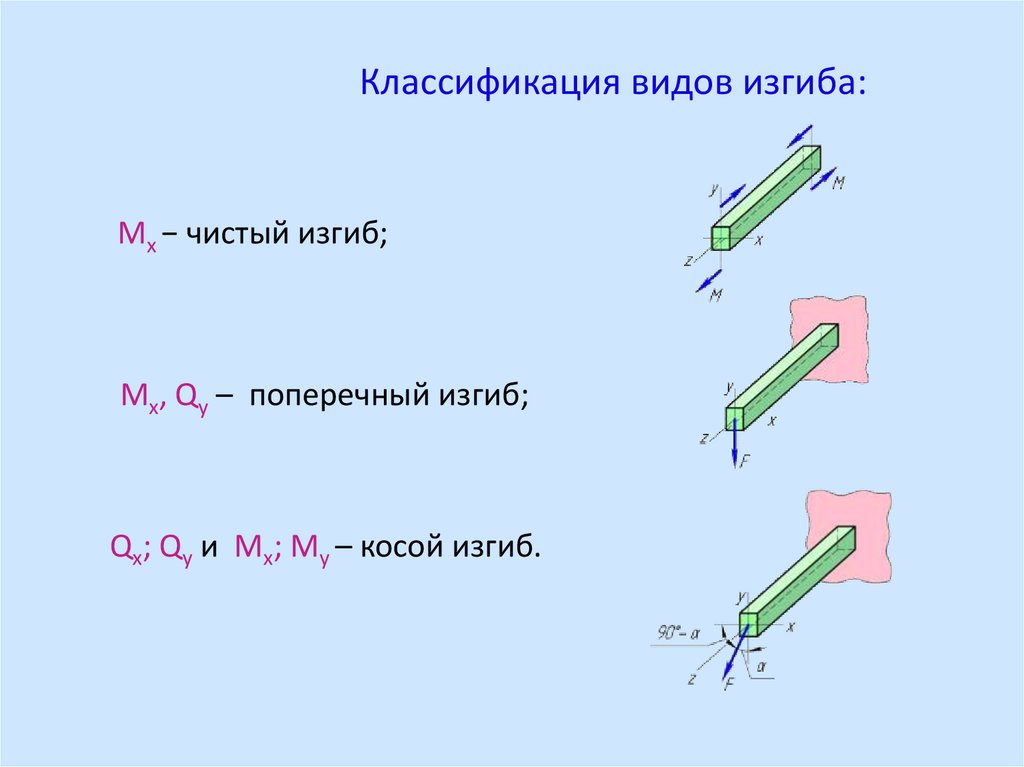
Классификация видов изгиба:
Мх − чистый изгиб;
Мх, Qy – поперечный изгиб;
Qх; Qy и Мх; Мy – косой изгиб.

8.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ИЗГИБЕ
1. ∑У = 0; RА − F1 + Qу = 0;
Qу = − RА + F1 = ∑ Fiγ;
2. ∑M¡ = 0; R · z − F1 · (z − a1) − Mи = 0;
Mи = R A· z − F1 · (z − a1) = ∑M (F¡);
Поперечная сила в произвольном сечении балки численно равна
алгебраической сумме проекций всех внешних сил, действующих на
отсеченной части на соответствующую ось.
Qу Fiy ;
Изгибающий момент в произвольном сечении балки численно
равен алгебраической сумме моментов всех внешних сил,
приложенных к отсеченной части.
M и mi ;

9. ПРАВИЛО ЗНАКОВ

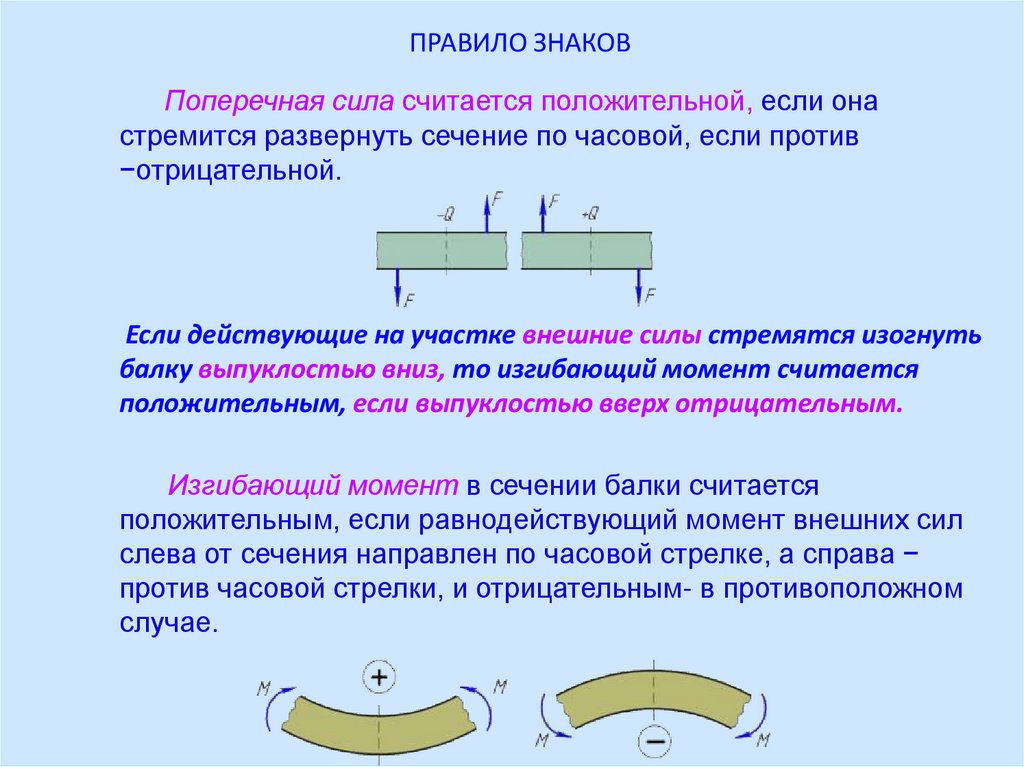
Поперечная сила считается положительной, если она
стремится развернуть сечение по часовой, если против
−отрицательной.
Если действующие на участке внешние силы стремятся изогнуть
балку выпуклостью вниз, то изгибающий момент считается
положительным, если выпуклостью вверх отрицательным.
Изгибающий момент в сечении балки считается
положительным, если равнодействующий момент внешних сил
слева от сечения направлен по часовой стрелке, а справа −
против часовой стрелки, и отрицательным- в противоположном
случае.

10. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ

Поперечная сила равна производной от
изгибающего момента по длине балки:
dM x
Q.
dz
Интенсивность распределенной нагрузки
равна производной от поперечной силы по
длине балки:
dQ
q.
dz

11. ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ

ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
ПО ХАРАКТЕРНЫМ СЕЧЕНИЯМ
Характерными являются сечения балки, где
приложены сосредоточенные силы и моменты, а
также сечения, ограничивающие участки с
равномерно распределенной нагрузкой.
Для эпюры поперечных сил − сечения, сделанные
слева и справа от точки приложения сосредоточенной
силы.
Для эпюры изгибающих моментов − сечения,
сделанные в точках приложения сосредоточенной
силы и слева и справа от точки приложения
сосредоточенного момента.

12.

13.

14. ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ

На основании метода сечений и
дифференциальных зависимостей
устанавливается взаимосвязь эпюр
Мx и Qy между собой и с внешней
нагрузкой, поэтому достаточно
вычислить ординаты эпюр для
характерных сечений и соединить их
линиями.

15. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР

1. На участке нагруженном равномерно распределенной нагрузкой:
- эпюра Q изображается прямой, наклонной к оси балки;
- эпюра М изображается квадратичной параболой.
2. На участке, свободном от распределенной нагрузки:
- эпюра Q изображается прямой, параллельной оси балки;
- эпюра М изображается прямой линией.
3. В сечении балки, где приложена сосредоточенная пара сил:
- Q поперечная сила не изменяет значения;
- М изгибающий момент меняется скачкообразно на значение, равное моменту
приложенной пары .
4. В сечении, где приложена сосредоточенная сила:
- значение Q меняется скачкообразно на значение, равное приложенной силе;
- на эпюре М будет излом.
5. В сечении на конце балки:
- Q равна приложенной силе или реакции в заделке.
- М равен нулю, за исключением случаев, когда в этом сечении приложен
сосредоточенный момент.

16. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР

1. На участке нагруженном равномерно
распределенной нагрузкой:
- эпюра Q изображается прямой, наклонной к оси
балки;
- эпюра М изображается квадратичной параболой.
2. На участке, свободном от распределенной
нагрузки:
- эпюра Q изображается прямой, параллельной оси
балки;
- эпюра М изображается прямой линией.

17. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР

3. В сечении балки, где приложена сосредоточенная пара
сил:
- Q поперечная сила не изменяет значения;
- М изгибающий момент меняется скачкообразно на
значение, равное моменту приложенной пары .
4. В сечении, где приложена сосредоточенная сила:
- значение Q меняется скачкообразно на значение, равное
приложенной силе;
- на эпюре М будет излом.
5. В сечении на конце балки:
- Q равна приложенной силе или реакции в заделке.
- М равен нулю, за исключением случаев, когда в этом
сечении приложен сосредоточенный момент.

18. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР Ми

1. На участке нагруженном равномерно
распределенной нагрузкой:
- эпюра М изображается квадратичной параболой.
2. На участке, свободном от распределенной
нагрузки:
- эпюра М изображается прямой линией.
3. В сечении балки, где приложена сосредоточенная
пара сил:
- М изгибающий момент меняется скачкообразно на
значение, равное моменту приложенной пары .
4. В сечении, где приложена сосредоточенная сила:
- на эпюре М будет излом.
5. В сечении на конце балки:
- М равен нулю, за исключением случаев, когда в
этом сечении приложен сосредоточенный момент.

19. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР Q y

1. На участке нагруженном равномерно
распределенной нагрузкой:
- эпюра Q изображается прямой, наклонной к оси балки;
- 2. На участке, свободном от распределенной нагрузки:
- эпюра Q изображается прямой, параллельной оси балки;
- 3. В сечении балки, где приложена сосредоточенная
пара сил:
- Q поперечная сила не изменяет значения;
- 4. В сечении, где приложена сосредоточенная сила:
- значение Q меняется скачкообразно на значение, равное
приложенной силе;
- 5. В сечении на конце балки:
- Q равна приложенной силе или реакции в заделке.

20. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой вид деформации называют изгибом?
2. Какие внутренние силовые факторы возникают при чистом изгибе?
3. Какие внутренние силовые факторы возникают в сечении балки при поперечном
изгибе?
4. Что делается с продольными волокнами балки при изгибе?
5. Какой слой волокон балки называется нейтральным?
6. Чему равна поперечная сила?
7. Чему равен изгибающий момент?
8. Как определятся знак поперечных сил и изгибающих моментов?
9. Для чего строятся эпюры поперечных сил и изгибающих моментов?
10. В каком поперечном сечении на эпюре поперечных сил будет скачок?
11. В каком поперечном сечении на эпюре изгибающих моментов будет скачок?
12. Какую плоскость называют силовой?
13.Вставьте пропущенные слова:
- при чистом изгибе в поперечных сечениях балки возникает в.с.ф. …………
- при прямом изгибе в поперечных сечениях балки возникают в.с.ф…………

21. ДОМАШНЕЕ ЗАДАНИЕ

Тема 2.6
ИЗГИБ ПРЯМОГО БРУСА
Автор - В.П. Олофинская
Техническая механика
Стр.239-255.