Атомная физика Магнитный момент атома Атом во внешнем магнитном поле

1.

Физика. 2 курс. 4 семестр
Специалитет
Лекция 10. Атомная физика
Магнитный момент атома
Атом во внешнем магнитном поле
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела, параграфа
Номер
слайда
Введение
3
Раздел 1. Магнитный момент атома
4
1.1. Связь магнитного и механического моментов (гиромагнитное отношение)
5
1.2. Орбитальный магнитный момент атома
6
1.3. Спиновый магнитный момент атома
7
1.4. Полный магнитный момент атома. Фактор Ланде.
8
1.5. Фактор Ланде: примеры
9
Раздел 2. Атом во внешнем магнитном поле
10
2.1. Расщепление энергетических уровней
11
2.2. Простой эффект Зеемана
13
2.3. Сложный эффект Зеемана
14
Дополнение (часто встречающийся вопрос при решении задач)
15
2

3.

Введение
В предыдущих 8-ой и 9-ой лекциях были рассмотрены моменты электрона и многоэлектронного
атома: орбитальный, собственный (спиновый), полный. См. лекцию 8, сл.13 и лекцию 9, раздел 1. Эти
моменты принято называть механическими, т.к. они объясняются (в полуклассическом приближении,
т.е. очень условно и очень грубо) движением электрона по орбитам и вращением вокруг своей оси,
соответственно.
В 10-ой лекции рассматриваются магнитные моменты атома, которые также можно объяснить (не
менее условно и не менее грубо) полу-классической аналогией – возникновением магнитного поля
при ускоренном движении заряженной частицы-электрона.
В разделе 1 даются основные формулы магнитных моментов атома: орбитального, собственного
(спинового) и полного, – определяется связь магнитных и механических моментов.
В разделе 2 рассматривается расщепление спектральных линий атома во внешнем магнитном
поле, обусловленное расщеплением энергетических уровней и появлением дополнительных
переходов между ними – эффект Зеемана.
3

4.

Раздел 1. Магнитный момент атома
4

5.

1. Магнитный момент атома
1.1. Связь магнитного и механического моментов (гиромагнитное отношение)
Из наглядного полуклассического представления о движении заряженной частицы-электрона по
окружности можно получить связь механического момента М и магнитного момента μ:
μ =-
М
Выполните это самостоятельно, используя, при необходимости,
учебник И.Е.Иродова, параграф 2.4 или лекцию 8.
В квантовой физике эта связь моментов остаётся справедливой. Вновь – посмотрите учебник И.Е.Иродова.
Важное замечание ! В лекции 8 магнитный момент обозначен как Pm, здесь и далее используется обозначение μ как это
принято в современной физической литературе по квантовой (атомной, ядерной) физике. Pm ≡ μ.
Полезные следствия:
1. Векторы магнитного и механического моментов противоположны друг другу по направлению
(знак «минус» в формуле) из-за разнонаправленности «движения» электрона и тока (объясните это).
2. Отношение модулей магнитного и механического моментов является универсальной
константой, остающейся неизменной в любых ситуациях и условиях и действующей для любых
моментов – орбитальных, собственных (спиновых), полных:
γ
е – заряд электрона, m – масса электрона
Величина γ называется гиромагнитным отношением электрона.
Замечание: формула для γ записана в системе СИ. В СГСЭ в знаменателе появится скорость света с. Будьте внимательны.
5

6.

1. Магнитный момент атома
1.2. Орбитальный магнитный момент атома
Вначале вспомним формулу орбитального механического момента атома (см. лекцию 9, раздел 1):
L – суммарное квантовое число атома.
ML = ℏ√L(L + 1).
Используя связь магнитного и механического моментов μL = - γ∙МL (см. предыдущий слайд), получим
выражение для магнитного момента:
μL = - γ∙ℏ√L(L + 1) = - μБ ∙√L(L + 1) ,
где μБ = γ∙ℏ =
.
Величина μБ называется магнетон Бора (ср. с лекцией 8). Физический смысл магнетона Бора – это
квант магнитного момента, по аналогии с ℏ – квантом многих других физических величин.
Используя тот же подход, как для орбитального магнитного момента, нетрудно получить формулу
для проекции орбитального магнитного момента на произвольную ось Z; в нашем случае, ось Z – это
направление внешнего магнитного поля:
μLZ = - μБ ∙mL.
(проделайте это самостоятельно)
Квантовые числа L и mL остались неизменными как для механического, так и для магнитного
орбитальных моментов:
- L может принимать только целочисленные положительные значения и 0, но с учётом ограничений
«сверху» (Lmax) и «снизу» (Lmin).
(Вспомните об этих ограничениях – см. лекцию 9).
6
- mL рассчитывается для каждого значения L и составляет: mL = 0, ±1, ±2, … , ±L.

7.

1. Магнитный момент атома
1.3. Спиновый магнитный момент атома
Известно, что магнитный момент создаётся при круговом или вращательном движении заряженной
частицы. Значит, магнитный момент электрона и атома в целом будет создаваться не только «вращением
электрона вокруг ядра», но и «вращением электрона вокруг своей оси», т.е. вследствие наличия у
электрона спина. Прошу помнить, что эти «вращения» очень-очень условны.
Вновь используя тот же подход, как для орбитального магнитного момента (см. предыдущий слайд),
можно получить такие же формулы для спинового магнитного момента – только с заменой квантового
числа L на квантовое число S. Но эксперимент потребовал внести поправку – коэффициент 2.
μS = - 2μБ ∙√S(S + 1)
μSZ = - 2μБ ∙mS
На физическом жаргоне: «Спин обладает удвоенным магнетизмом».
Квантовые числа S и mS остались неизменными как для механического, так и для магнитного
спиновых моментов:
S = Ns, Ns - 1, Ns - 2, … , Smin
где N – число «неспаренных» электронов в атоме, s = 1/2 .
Smin = 0, если N - чётное число,
Smin = 1/2, если N - нечётное число.
mS = S, S-1, S-2, … , -S.
при S = 1/2 →
mS = +1/2 и -1/2 .
7

8.

1. Магнитный момент атома
1.4. Полный магнитный момент атома. Фактор Ланде.
Известно, что механические моменты: орбитальный и спиновой, - образуют полный механический
момент. Точно так же происходит с магнитными моментами. Но если механические моменты складываются
«чистыми» (чисто орбитальный + чисто спиновый), то для магнитных моментов характерно «смешение»,
которое учитывается множителем или фактором Ланде g:
L, S, J – квантовые числа: орбитальное, спиновое и полное; рассчитываются
по «обычным» формулам для механических моментов
Формулы для полного магнитного момента и его проекции на ось Z таковы:
μ = - μБ ∙g∙√J(J + 1)
Сравните с формулами для ML и для mL
μZ = - μБ ∙g∙mJ
mJ = J, J-1, J-2, … , -J.
и найдите два отличия.
Примеры: а). при S = 0 → g = 1;
б). при L = 0 → g = 2.
Расчёт фактора Ланде в некоторых интересных случаях:
1. Состояние 4D1/2 → g = 0, механический момент есть, магнитный момент отсутствует.
2. Состояние 6F1/2 → g = - 2/3, магнитный и механический моменты сонаправлены: «минус на минус даёт плюс».
3. Состояние 5P1 → g = 5/2, т.е. фактор Ланде может быть более 2.
Выполните проверку значений g самостоятельно. Также: рассчитайте фактор Ланде для состояния 3Р0 ,
попробуйте объяснить полученный результат (он не будет тривиальным).
8

9.

1. Магнитный момент атома
1.5. Фактор Ланде: примеры
Несколько экспериментальных значений фактора Ланде g:
Как видите, орбитальный момент L для этих атомов равен практически нулю – см. пример б) на
предыдущем слайде. Магнитные свойства их определяет почти полностью спиновый момент S. Подумайте,
почему это так.
9

10.

Раздел 2. Атом во внешнем магнитном поле
10

11.

2. Атом во внешнем магнитном поле
2.1. Расщепление энергетических уровней
Очевидно, что атом, обладающий магнитным моментом, должен взаимодействовать
с внешним магнитным полем.
Экспериментально этот эффект был обнаружен Зееманом (1896 год): спектральные
линии атома, после помещения его во внешнее магнитное поле, испытывали расщепление –
эффект Зеемана. (Произносить следует – Земан, одно е, ударение на первом слоге.)
Объяснение расщепления линий спектра могло быть одно: происходит расщепление
соответствующих энергетических уровней атома, т.е. появляются новые подуровни, переходы между
которыми дают эти дополнительные линии, наблюдаемые в эксперименте.
Причина расщепления энергетических линий состоит в следующем: атом, обладающий магнитным
моментом, приобретает или теряет в магнитном поле дополнительную энергию ΔЕ:
ΔЕB = -μZ ∙В
где В – магнитная индукция внешнего поля, вектор;
μZ – проекция магнитного момента атома на ось z, т.е. на вектор В.
Используя формулу для проекции полного магнитного момента (см. сл.8), получим энергию
подуровней в зависимости от квантового числа mJ:
Е = Е0 + ΔЕB = Е0 + μБ∙g∙В∙mJ
mJ = J, J-1, J-2, … , -J; всего (2J + 1) значений.
Е0 – энергия уровня в отсутствие магнитного поля.
Остальные обозначения – см. на слайде 8.
μБ - магнетон Бора.
Продолжение →
11

12.

2. Атом во внешнем магнитном поле
2.1. Расщепление энергетических уровней
Из красной формулы (предыдущий слайд) следует, что первоначальный энергетический уровень атома Е0 ,
соответствующий полному квантовому числу, J в магнитном поле распадётся (расщепится) на (2J+1)
подуровней, т.е. по количеству значений mJ .
Все подуровни энергетически равноотстоят друг от друга.
Покажите сами.
Интервалы между соседними подуровнями (δЕ) больше для более сильного поля (высокое значение В)
и для высокого значения фактора Ланде g, т.к. δЕ ~ В, δЕ ~ g.
Правила перехода между «магнитными» подуровнями.
1. Переходы между подуровнями возможны, если они принадлежат разным уровням.
2. При переходах между подуровнями должно соблюдаться стандартное правило отбора:
ΔmJ = 0, ±1.
3. Частота, соответствующая переходу между подуровнями разных уровней, ω, определяется так:
ω = ω0 + Δω, где ω0 – частота перехода между уровнями, основная частота;
Δω – зеемановское смещение относительно основной частоты ω0 .
Δω = (m2∙g2 – m1∙g1)∙δω0, где δω0 = μБ∙В/ℏ – лоренцево смещение;
Получите эту формулу сами!
mJ, g – квантовое число и фактор Ланде начального (1) и конечного (2) уровня, соответственно.
Полученные формулы нужны для анализа эффекта Зеемана (расщепление линий в магнитном поле).
12

13.

2. Атом во внешнем магнитном поле
2.2. Простой эффект Зеемана
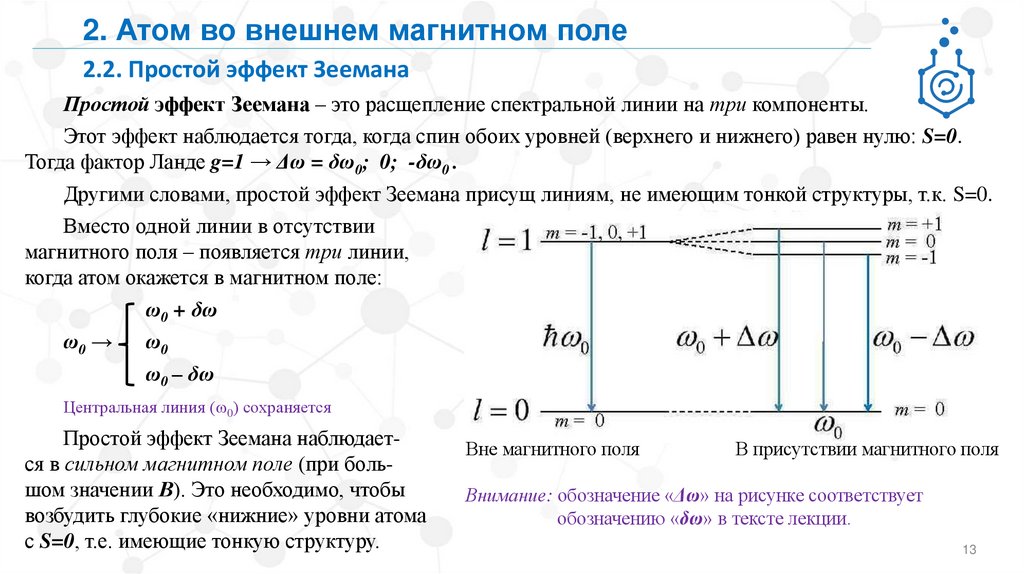
Простой эффект Зеемана – это расщепление спектральной линии на три компоненты.
Этот эффект наблюдается тогда, когда спин обоих уровней (верхнего и нижнего) равен нулю: S=0.
Тогда фактор Ланде g=1 → Δω = δω0; 0; -δω0 .
Другими словами, простой эффект Зеемана присущ линиям, не имеющим тонкой структуры, т.к. S=0.
Вместо одной линии в отсутствии
магнитного поля – появляется три линии,
когда атом окажется в магнитном поле:
ω0 + δω
ω0 →
ω0
ω0 – δω
Центральная линия (ω0) сохраняется
Простой эффект Зеемана наблюдается в сильном магнитном поле (при большом значении В). Это необходимо, чтобы
возбудить глубокие «нижние» уровни атома
с S=0, т.е. имеющие тонкую структуру.
Вне магнитного поля
В присутствии магнитного поля
Внимание: обозначение «Δω» на рисунке соответствует
обозначению «δω» в тексте лекции.
13

14.

2. Атом во внешнем магнитном поле
2.3. Сложный эффект Зеемана
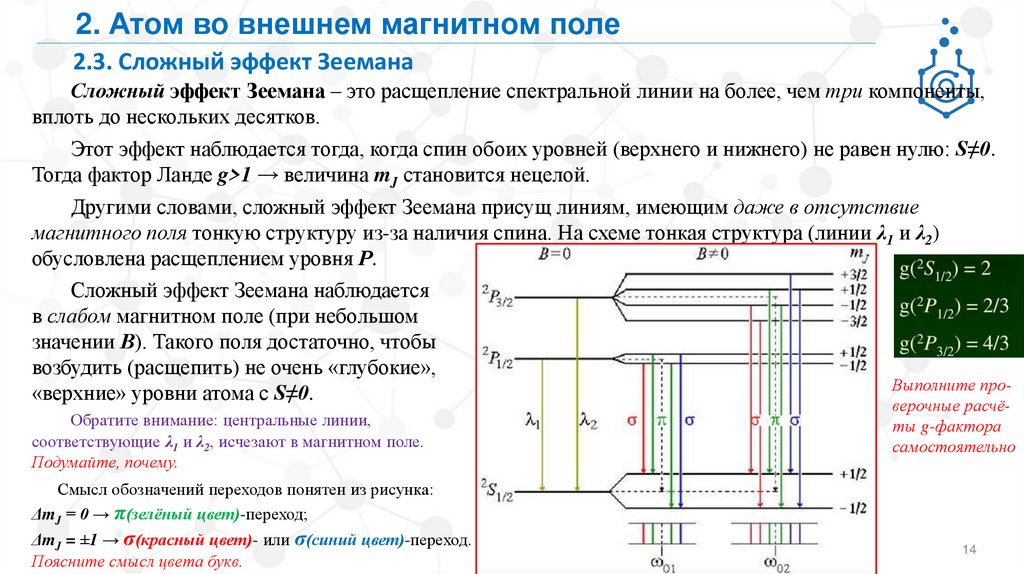
Сложный эффект Зеемана – это расщепление спектральной линии на более, чем три компоненты,
вплоть до нескольких десятков.
Этот эффект наблюдается тогда, когда спин обоих уровней (верхнего и нижнего) не равен нулю: S≠0.
Тогда фактор Ланде g>1 → величина mJ становится нецелой.
Другими словами, сложный эффект Зеемана присущ линиям, имеющим даже в отсутствие
магнитного поля тонкую структуру из-за наличия спина. На схеме тонкая структура (линии λ1 и λ2)
обусловлена расщеплением уровня Р.
Сложный эффект Зеемана наблюдается
в слабом магнитном поле (при небольшом
значении В). Такого поля достаточно, чтобы
возбудить (расщепить) не очень «глубокие»,
Выполните про«верхние» уровни атома с S≠0.
Обратите внимание: центральные линии,
соответствующие λ1 и λ2, исчезают в магнитном поле.
Подумайте, почему.
верочные расчёты g-фактора
самостоятельно
Смысл обозначений переходов понятен из рисунка:
ΔmJ = 0 → π(зелёный цвет)-переход;
ΔmJ = ±1 → σ(красный цвет)- или σ(синий цвет)-переход.
Поясните смысл цвета букв.
14

15.

2. Атом во внешнем магнитном поле
Дополнение: часто встречающийся вопрос при решении задач
Траектория движения пучков атомов в опыте Штерна и Герлаха
внутри магнитов – см. рисунок.
Движение атомов надо разложить по оси y и по оси z.
В горизонтальном направлении (ось у) движение равномерное,
с постоянной скоростью, по инерции. Почему?
В вертикальном направлении (ось z) движение равноускоренное,
с нарастающей скоростью, т.е. по параболе. Причина – действие силы
на пучок в вертикальном направлении, возникающей из-за градиента магнитного поля:
MZ – проекция спинового момента атома на ось z.
В результате, отклонение от первоначального горизонтального направления нарастает как ~t2.
После выхода из магнитов, т.е. за пределами прямоугольника на рисунке, действие магнитной силы
прекращается. Дальнейшее движение – полёт по инерции по прямолинейной траектории с сохранением
угла вылета α, сформировавшегося к моменту выхода за пределы магнитного поля.
Обратите внимание: в эффекте Зеемана происходит расщепление энергетических уровней атома, пучок самих атомов
пространственно не разделяется. В опыте Штерна и Герлаха пространственно разделяется сам пучок электронейтральных атомов
15
из-за наличия нескомпенсированного спина у атомов: либо +1/2, либо -1/2.
α

16.

Спасибо за внимание