Similar presentations:
Истечение жидкостей, паров и газов
1.
Истечение жидкостей, паров и газовВ общем случае процессы истечения удобно
рассматривать как теоретические обратимые процессы
истечения: политропный или адиабатный, а переход к
реальным процессам осуществлять путем введения
соответствующих поправочных коэффициентов,
определяемых опытным путем
Основной задачей при изучении процессов
истечения является определение линейной (с) и
массовой скорости (и), расхода (G), параметров и
функций состояния рабочего тела (p, v, t, u, h, s) вдоль
канала.
2.
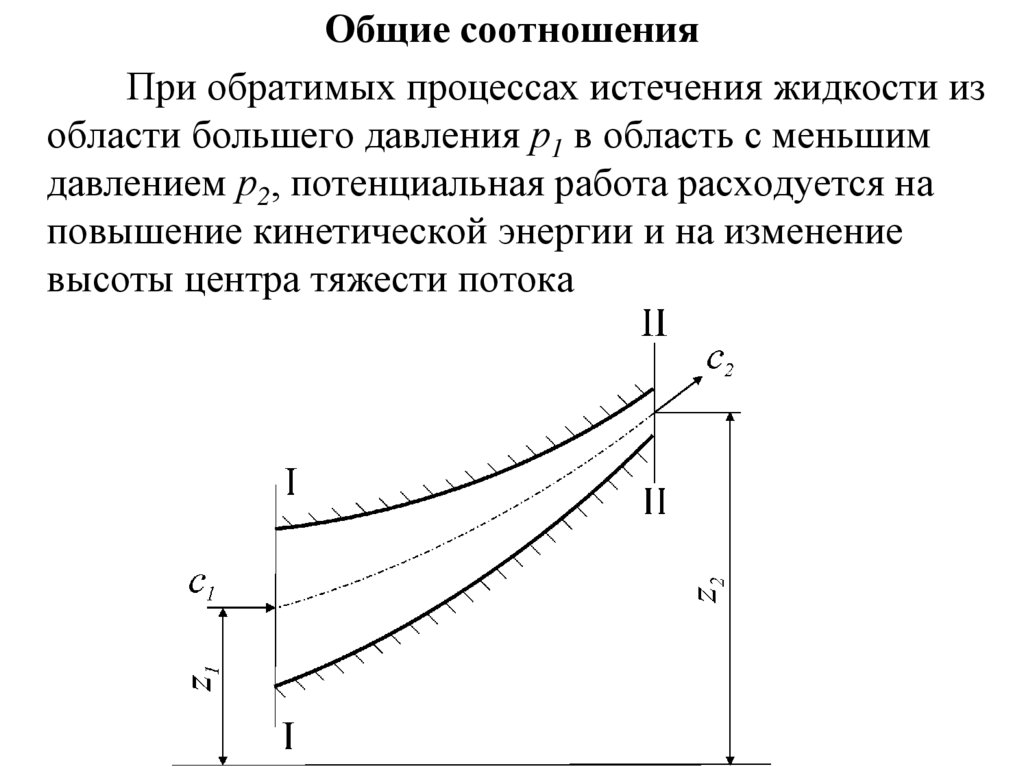
Общие соотношенияПри обратимых процессах истечения жидкости из
области большего давления р1 в область с меньшим
давлением р2, потенциальная работа расходуется на
повышение кинетической энергии и на изменение
высоты центра тяжести потока
3.
Дифференциальное уравнение распределения удельнойпотенциальной работы, при отсутствии эффективной
потенциальной работы потока ( w* 0 ), будет
выглядеть следующим образом
w vdp cdc gdz
w1,2
2
c2
2
2
c1
2
g ( z2 z1 )
Отсюда теоретическая линейная скорость истечения
жидкости в выходном сечении сопла (с2)
c2 c 2w1, 2 2 g ( z2 z1 )
2
1
4.
Сопла или штуцеры, через которые происходятпроцессы истечения, обычно выполняются короткими,
поэтому работой, идущей на изменение центра тяжести
поток, 2 g z 2 z1
можно пренебречь. При этом
условии теоретическая линейная скорость истечения
жидкости в выходном сечении сопла может быть
определена из соотношения
c2
2
c1 2 w1,2
5.
Скорость потока на входе в сопло может бытьвычислена, в свою очередь, как теоретическая скорость
истечения из воображаемого нулевого состояния
(точка 0), в котором жидкость находится в состоянии
покоя (с0=0), до заданного начального состояния (1),
линейная скорость потока во входном сечении сопла
определяется по формуле
c1
2
c0 2 w0 ,1
2 w0 ,1
6.
Сумма потенциальных работ w0,1 и w1,2, представляетсобой потенциальную работу жидкости (сжимаемой или
несжимаемой) в обратимом адиабатном процессе
истечения от нулевого состояния (с0 =0), определяемого
параметрами торможения, до конечного давления p2
( w0 ,2 w0 ,1 w1,2 ).
Следовательно, соотношение для определения
линейной теоретической скорости обратимого
адиабатного процесса истечения жидкости можно
записать следующим образом
с2 2 w0 ,2
7.
Важной характеристикой потока является его массоваяскорость, численно равная секундному расходу
жидкости через единицу площади поперечного сечения
потока w0 ,2 w0 ,1 w1,2 ( и, кг/(м2 с))
G
u
f
Связь между массовой и линейной скоростью
u 2 c2 2
В соответствии с принципом неразрывности потока,
массовый расход вещества (G) в любом поперечном
сечении канала одинаков
G c f u f idem
8.
Истечение несжимаемых жидкостейНесжимаемая жидкость имеет практически неизменную
плотность при любых давлениях и температурах.
Соотношения для определения удельной потенциальной
работы несжимаемой жидкости в обратимых процессах
истечения
p0 p2
1 0
w0 ,2 vdp dp
2
0
2
9.
Теоретическая линейная скорость истечениянесжимаемой жидкости в выходном сечении сопла (с2)
p1 p2
с2 2
Массовая скорость потока несжимаемой жидкости на
выходе из сопла
u 2 c2 2 p0 p2 .
С увеличением по длине канала (x) разности давления
(р0 - рx), повышается массовая скорость потока. При
этом площадь проходного сечения канала, должна
непрерывно уменьшаться (G = idem). Следовательно,
при истечении несжимаемой жидкости следует
применять суживающиеся сопла.
10.
Истечение сжимаемых жидкостейК классу сжимаемых жидкостей относятся вещества,
плотность которых изменяется в зависимости от
давления и температуры. Газы (идеальные и реальные)
относятся к классу сжимаемых жидкостей.
Потенциальная работа обратимого адиабатного
процесса истечения газа от нулевого до конечного
состояния (0-2)
k 1
p2 k
k
w0 ,2
p0 v0 1
p0
k 1
k 1
k
p2
2k
c2 2 w0 ,2
p0 v0 1
p0
k 1
11.
Для вычисления массовой скорости газа u 2 c2 2необходимо знать плотность газа в выходном сечении
сопла, значение которой определяется из уравнения
адиабаты
1
1
p0k v0 p2k v2 ,
1
v ,
1
k
1 p2
2
v0 p0
k 1
p2 k
2k
c2 2 w0 ,2
p0 v0 1
p0
k 1
12.
1k 1
k
k
1
p
2к
p
2
и2 с2 2
p0 v0 1 2
p0 v
к 1
0 p0
k 1
2
2 к p0 p2 k p2 k
u2
1
к 1 v0 p0 p0
2
k 1
k
k
p2
2 k p0 p2
k 1 v0 p0
p0
2
к 1
2к p0
к к
к 1 v0
13.
Введем в уравнение характеристику расхода λ14.
15.
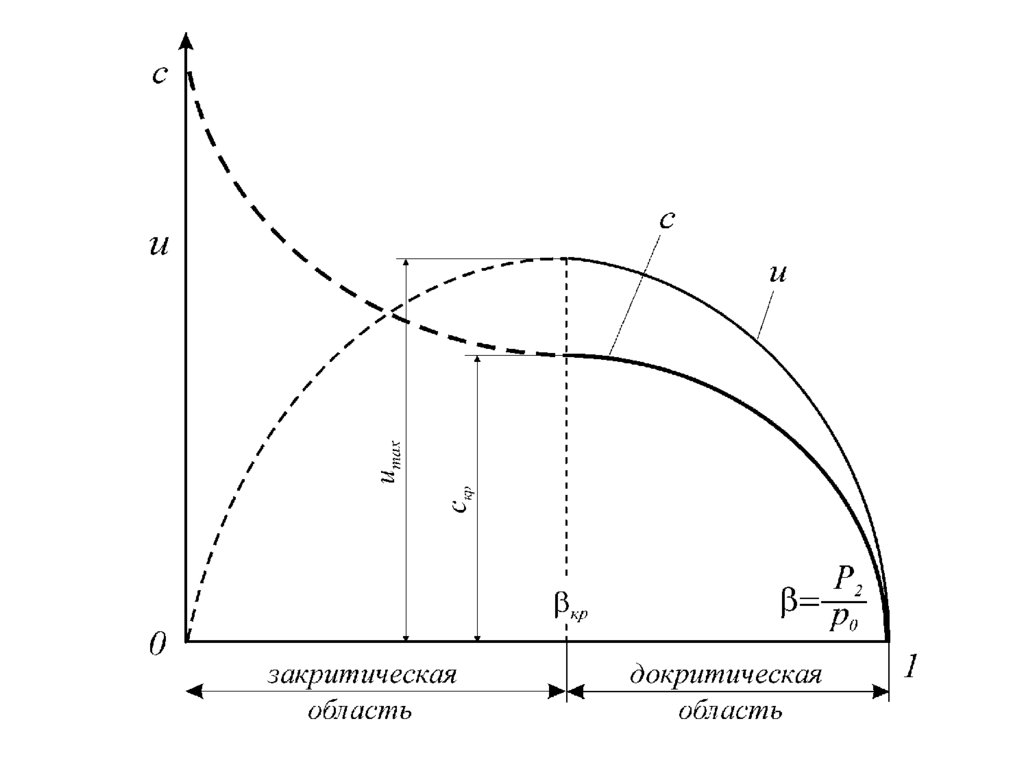
Анализ уравнения для массовой скорости потокапоказывает, что скорость газа изменяясь в зависимости
от соотношения давлений в процессе истечения p2 / p0
дважды обращается в нуль - при р2/р0 = 1 (нет
движения), а также при = 0 (истечение в вакуум,
р2 = 0).
Соотношение давлений, при котором массовая скорость
истечения становится максимальной ( umax ), называется
критическим кр , а режим истечения при этом
условии называется критическим режимом истечения.
16.
Критическое соотношение давлений и значениехарактеристики адиабатного расширения сжимаемых
жидкостей
k
k 1
2
кр
k 1
;
pv k
2
кр
p0 v0 k 1
17.
Критическая линейная скорость истеченияk
k
cкр 2
p0 v0 1 кр 2
p0 v0
k 1
k 1
p0 v0
pv кр
кр
cкр k ( pv )кр
18.
сд cДействительные скорости
u¶ = m ×u
φ - коэффициент скорости учитывающий реальный
процесс.
μ - коэффициент расхода.
Действительный расход
G¶ = c¶ × r × f¶ = j ×c× r × a × f
= 0,65 - 1- коэффициент сжатия струи
f¶
a=
f
19.
Для обратимого адиабатного истечения любойсжимаемой жидкости критическая линейная скорость
равна местной скорости звука в данной среде
a k ( pv )кр ;
c
M число Маха
a
Значение массовой критической скорости истечения
p0
u кр кр 2 ,
v0
кр
кр
2
k k 1
Для природных газов значения критических параметров
истечения изменяются в следующих диапазонах:
τкр=0,85 - 0,90;
βкр=0,53 - 0,56;
λкр=0,48 - 0,46.
20.
Область диаграммы кр 1 , в которой называетсяобластью докритического (дозвукового)режима
истечения. В этой области давление потока в выходном
сечении сопла (p2) равно давлению среды (pср), в
которую происходит истечение (p2=pср), а при
снижении давления среды (pср) наблюдается увеличение
массового расхода через сопло (G), а также линейной
(c) и массовой (и) скорости потока в выходном сечении
сопла.
21.
После достижения критического соотношениядавлений ( кр ) наступает критический (звуковой)
режим истечения, при котором на выходе из сопла
устанавливается критическое давление режима
( p2 pкр p0 кр ). Этот режим характеризуется
критическими значениями массового расхода (Gкр),
линейной (c2=cкр) и массовой (и2=икр) скорости
истечения в выходном сечении сопла.
22.
Дальнейшее снижение давления среды (pср), в которуюпроисходит истечение вещества, не приводит к снижению
давления на выходе из сопла, которое остается неизменным
и равным критическому давлению (c2=cкр). Это явление
называется «кризисом течения». В критическом режиме
истечения скорость потока в выходном сечении сопла
устанавливается равной местной скорости звука в данной
среде (с2=скр=a). С этой же скоростью (скоростью звука) в
среде распространяется любое возмущение.
Установившаяся в выходном сечении сопла критическая
скорость истечения (cкр) препятствует подходу волны
разряжения к этому сечению сопла, что и предопределяет
стабилизацию линейной скорости истечения на уровне
критического значения даже при дальнейшем снижении
давления среды. При данных условиях истечения
( pср p2 pкр ) для увеличения кинетической энергии
потока используется не весь располагаемый перепад
давления ( p0 pср ), а только часть его ( p0 p2 ).
23.
Таким образом, при истечении через суживающиеся сопла иотверстия в тонких стенках возможны только два режима
истечения - докритический и критический. Процесс
истечения через суживающиеся сопла и отверстия в тонких
стенках возможен только при выполнении следующего
условия:
1 кр
Для обеспечения закритического режима истечения,
характеризующегося условием ( c2 cкр a ), необходимо
дополнить суживающееся сопло расширяющейся частью, в
выходном сечении которой возможно достичь значения
давления ниже критического ( p2 pкр ). Такое
комбинированное сопло называется соплом Лаваля.
В комбинированных соплах для увеличения кинетической
энергии потока может использоваться весь располагаемый
перепад давления ( p0 pср ).
24.
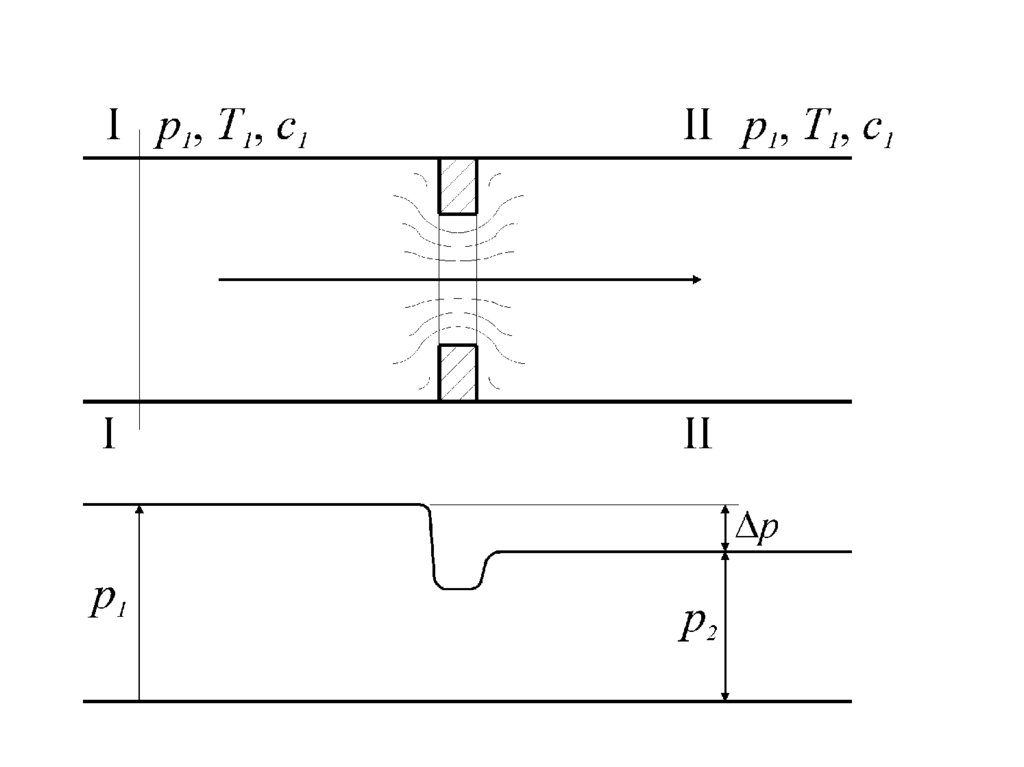
Дросселирование. Эффект Джоуля-ТомсонаЭффект падения давления потока рабочего тела в процессе
преодоления им (потоком) местного сопротивления
называется дросселированием.
Причинами возникновения местных сопротивлений при
движении потока рабочего тела по каналам могут быть
запорные, регулирующие и измерительные устройства;
повороты, сужение, загрязнение каналов и т.д.
Рассмотрим процесс дросселирования, протекающий без
внешней работы ( W1*,2 = 0), в котором отсутствует
теплообмен рабочего тела с внешней средой ( Q1*,2 = 0).
Падение давления за местным сопротивлением обусловлено
диссипацией (потерей) энергии потока, расходуемой на
преодоление этого сопротивления, то есть на работу
**
W
необратимых потерь (
1,2 ).
25.
26.
С учетом перечисленных условий рассматриваемогопроцесса дросселирования, уравнение первого начала
термодинамики для потока по балансу рабочего тела
Q Q dH W W
примет вид
H2 - H1 = 0 или .
H idem
Это значит, что рассматриваемый процесс
дросселирования является процессом изоэнтальпийным:
энтальпия рабочего тела до дросселя численно равна
энтальпии рабочего тела после дросселя. При течении
внутри дросселя энтальпия газа или пара меняется.
27.
Процесс дросселирования является процессомнеобратимым; он всегда сопровождается ростом энтропии
рабочего тела. Явление изменения температуры газа или
жидкости при адиабатном дросселировании называется
эффектом Джоуля – Томсона.
Различают дифференциальный и интегральный дроссель –
эффекты. Величина дифференциального дроссель –
эффекта определяется из соотношения
T
Dh
p h
где Dh – коэффициент дросселирования или коэффициент
Джоуля – Томсона, .
Интегральный дроссель-эффект определяется по
2
соотношению
T2 T1 Dh dp
1
28.
Коэффициент Джоуля – Томсона определяется изследующего уравнения, выведенного из математических
выражений первого начала термодинамики и второго начала
термостатики
v
T v
T p
Dh
.
cp
Знак дифференциального дроссель–эффекта (коэффициента
Джоуля – Томсона) определяется из анализа уравнения. В
зависимости от характера изменения температуры T, имеют
место три вида дроссель–эффекта (процесс дросселирования
всегда происходит с падением давления dp<0):
1. Дроссель–эффект положительный (Dh > 0), в этом случае
процесс дросселирования сопровождается снижением
температуры рабочего тела (dT<0);
29.
2. Дроссель–эффект отрицательный (Dh < 0), в этом случаепроцесс дросселирования сопровождается повышением
температуры рабочего тела (dT>0);
3. Дроссель–эффект равен нулю (Dh = 0), если в процессе
дросселирования температура рабочего тела не изменяется.
Нулевой дроссель-эффект наблюдается при
дросселировании идеального газа.
Для одного и того же вещества в зависимости от
значений параметров состояния коэффициент Джоуля –
Томсона Dh может иметь положительные, отрицательные
значения, а также быть равным нулю.
Состояние газа или жидкости, которому соответствует
условие Dh = 0, называется точкой инверсий.
Геометрическое место точек инверсии на диаграмме
состояния данного вещества называется кривой инверсии.
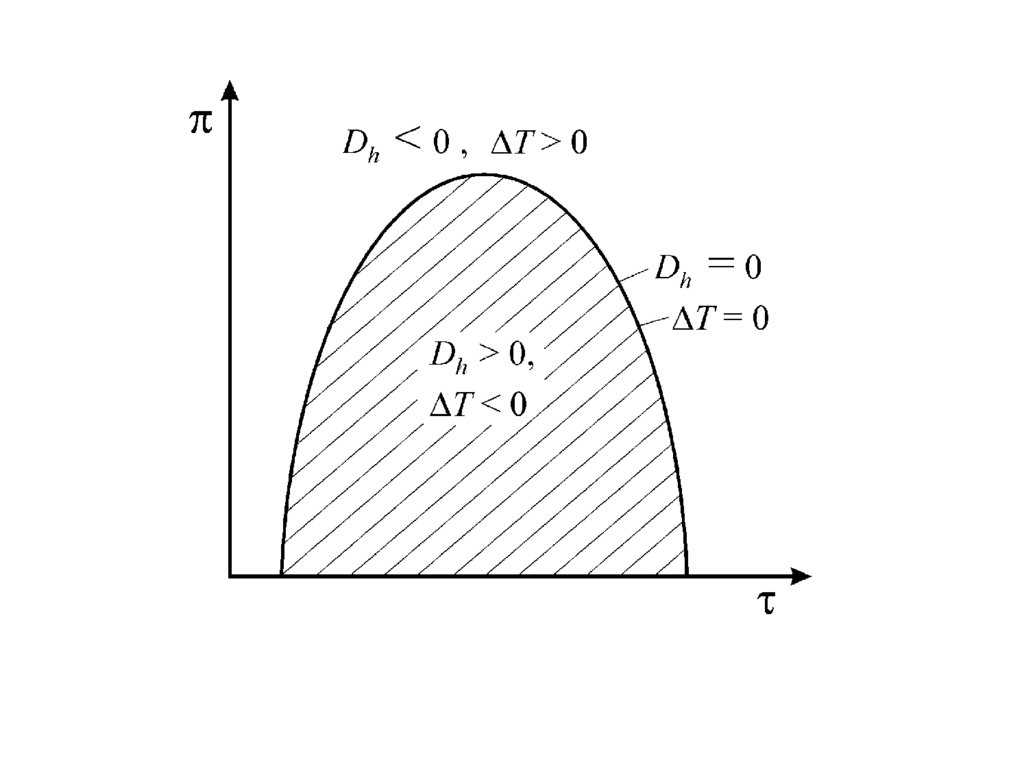
30.
Кривая инверсии описывается уравнениемv
v
T p T
Для каждого вещества в диаграмме р - v имеется своя
кривая инверсии. Закон соответственных состояний
позволяет построить обобщенные кривые инверсии для
групп термодинамически подобных веществ. Для
природных газов инверсионная диаграмма приведена на
графике в виде π = f(τ)










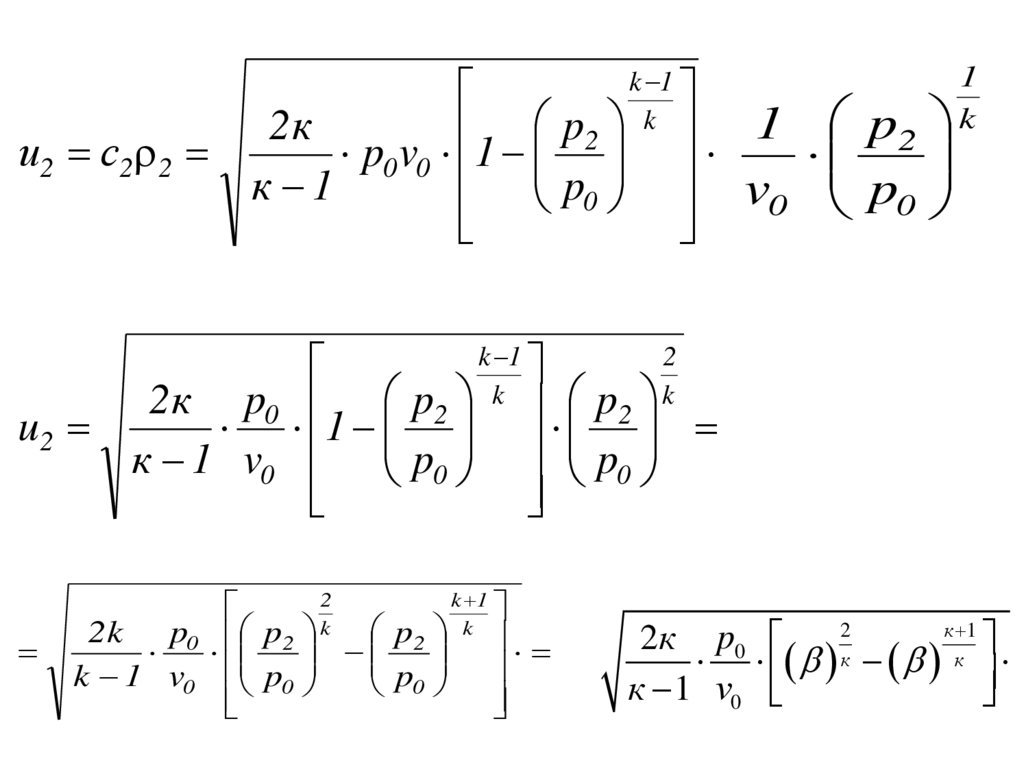
















 physics
physics








