Дербес туындылар және дербес туындылы теңдеулердің қолданылулары

1.

АЛМАТЫ ТЕХНОЛОГИЯЛЫҚ УНИВЕРСИТЕТІ
Тақырып: Дербес туындылар және дербес
туындылы теңдеулердің қолданылулары.
Жетекші: Абдиманапова Перизат
Орындағандар: Тлегенова Шұғыла,
Калдбаева Сарбиназ

2.

Жоспар:
1. Дербес туындылар және дербес туындылы теңдеулер туралы
жалпы түсінік.
2. Физикада қолданылуы:
a) Толқындар мен өрістер: Негізгі ұғымдар мен мысалдар.
b) Толқын теңдеуі: Шешілу жолдары және қолданылуы.
c) Өрістердегі теңдеулер: Лаплас және Пуассон теңдеулері.
3. Басқа салаларда қолданылуы.
4. Қорытынды.

3.

Дербес туындылар және дербес туынды теңдеулер
туралы жалпы түсінік.
Дербес туынды — бірнеше айнымалысы бар функцияның бір
айнымалы бойынша алынған туындысы. Басқа айнымалылар
тұрақты деп қарастырылады. Мысалы, u = f(x,y) функциясының x
бойынша дербес туындысы:
,
Дербес туындылы теңдеулер (ДТТ): Бұл теңдеулерде ізделінетін
функция бірнеше айнымалыдан тәуелді болады және оның
дербес туындылары қатысады. Мысалы: Толқындық теңдеу,
Лаплас теңдеуі, Пуассон теңдеуі.

4.

Физикада қолданылуы
Дербес туындылар физикада, техникада және математикада маңызды
рөл атқарады. Олар әртүрлі физикалық құбылыстарды сипаттауда
қолданылады, мысалы, толқындар мен өрістерді зерттеуде.
Толқындар мен өрістер:
Негізгі ұғымдар мен мысалдар: Толқын; Физикалық шаманың
кеңістікте және уақыт бойынша таралуы. Мысалы; дыбыс толқыны,
жарық толқыны. Өріс; Кеңістіктегі нүктелерге белгілі бір физикалық
шаманың сәйкес келуі. Мысалы; электр өрісі, магнит өрісі.
Дыбыс толқынының таралуын сипаттайтын теңдеу:
,

5.

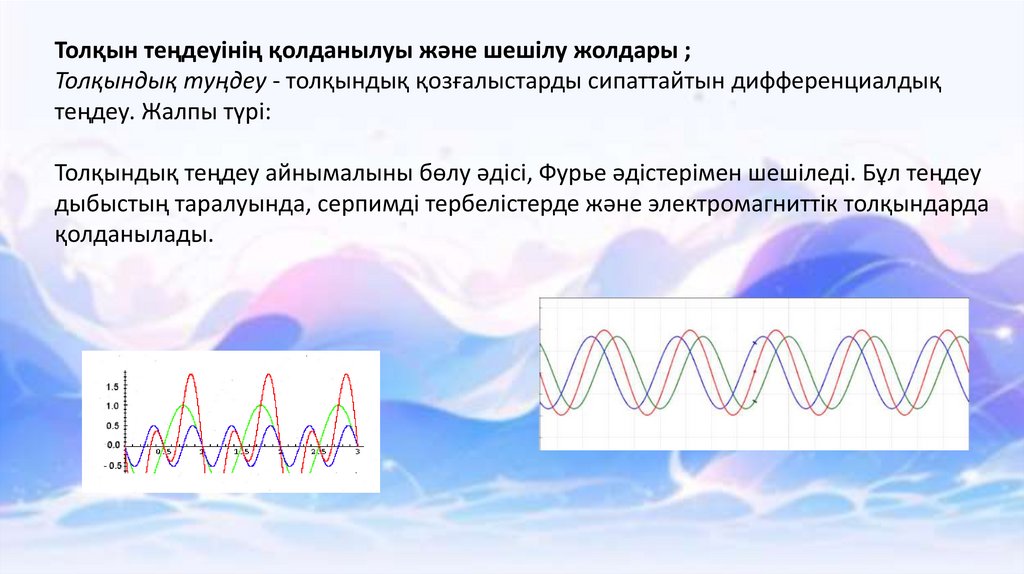
Толқын теңдеуінің қолданылуы және шешілу жолдары ;
Толқындық туңдеу - толқындық қозғалыстарды сипаттайтын дифференциалдық
теңдеу. Жалпы түрі:
Толқындық теңдеу айнымалыны бөлу әдісі, Фурье әдістерімен шешіледі. Бұл теңдеу
дыбыстың таралуында, серпимді тербелістерде және электромагниттік толқындарда
қолданылады.

6.

Толқындық теңдеулер электромагниттік және
механикалық құбылыстарды бейнелейді. Жылу
өткізгіштік құбылыстарын модельдеу үшін
жылу өткізгіштік теңдеуі қолданылады. Ал
кванттық механикада Шредингер теңдеуінің
маңызы зор.
Эрвин Шрёдингер
(1887 – 1961)
1926 жылы Шредингер де Бройль (бөлшектің толқын сияқты қасиеті
болады деген идея) тұжырымын негізге ала отырып, өзінің толқындық
теңдеуін жасады.Бұл теңдеу электрон, протон сияқты бөлшектердің
кеңістіктегі толқындық күйін сипаттайды.

7.

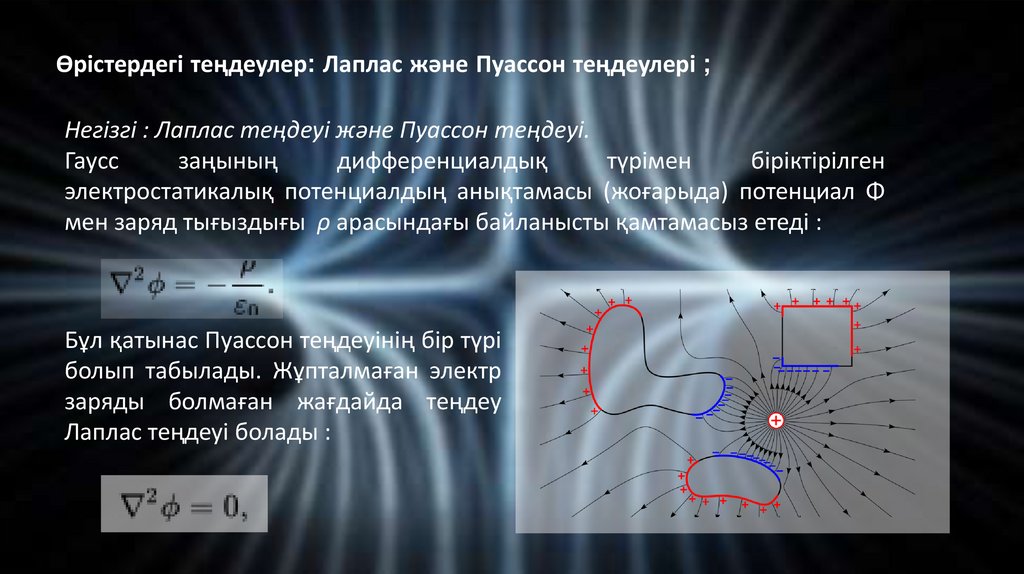
Өрістердегі теңдеулер: Лаплас және Пуассон теңдеулері ;
Негізгі : Лаплас теңдеуі және Пуассон теңдеуі.
Гаусс
заңының
дифференциалдық
түрімен
біріктірілген
электростатикалық потенциалдың анықтамасы (жоғарыда) потенциал Φ
мен заряд тығыздығы ρ арасындағы байланысты қамтамасыз етеді :
Бұл қатынас Пуассон теңдеуінің бір түрі
болып табылады. Жұпталмаған электр
заряды болмаған жағдайда теңдеу
Лаплас теңдеуі болады :

8.

Экзопланетаны жарық қисығы арқылы анықтау.
Джеймс Уэбб немесе Хаббл телескопы бір жұлдызды өзінің
телескопы менен ұзақ уақыт бақылайды. Егер сол
жұлдыздың жарығы бір сәтке бәсеңдесе, демек, алдыңғы
жағынан бір нәрсе (мысалы, планета) өткен. Ғалымдар осы
жарықтың бәсеңдеуін уақыт бойынша өлшейді, және
дербес туындыны қолданады. Бұл жерде жарық
интенсивтілігінің туындысы ∂I/∂t қолданылады:
Мұндағы I — жарық қарқындылығы, t — уақыт.
Егер ∂I/∂t ≠ 0, яғни жарық өзгерсе — онда планета бар
деген белгі.
Джеймс Уэбб ғарыштық телескопы
Джеймс Эдвард Уэбб
(1906 - 1992)

9.

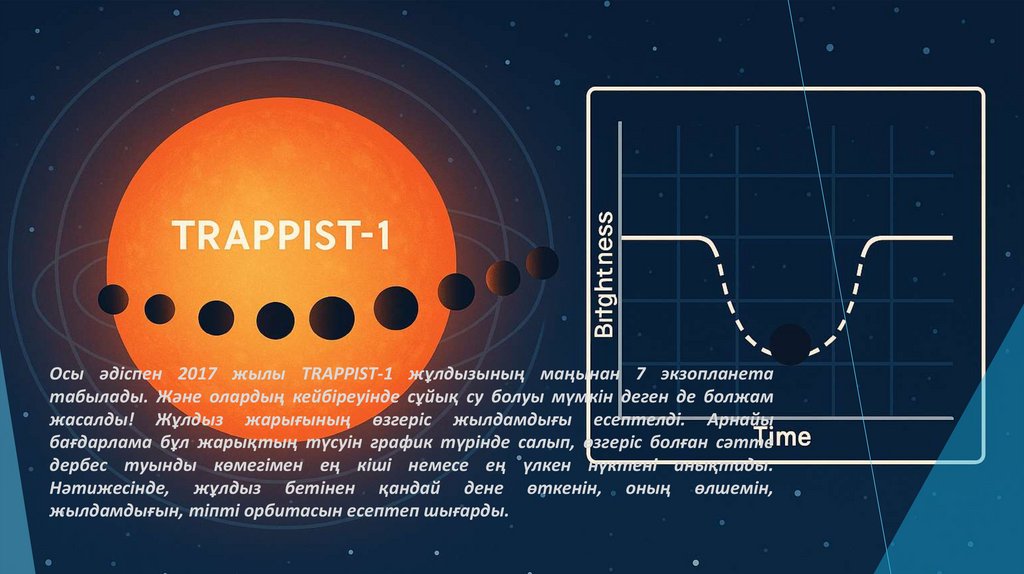
Осы әдіспен 2017 жылы TRAPPIST-1 жұлдызының маңынан 7 экзопланета
табылады. Және олардың кейбіреуінде сұйық су болуы мүмкін деген де болжам
жасалды! Жұлдыз жарығының өзгеріс жылдамдығы есептелді. Арнайы
бағдарлама бұл жарықтың түсуін график түрінде салып, өзгеріс болған сәтте
дербес туынды көмегімен ең кіші немесе ең үлкен нүктені анықтады.
Нәтижесінде, жұлдыз бетінен қандай дене өткенін, оның өлшемін,
жылдамдығын, тіпті орбитасын есептеп шығарды.

10.

Биологияда қолданылуы.
Томография – дененің ішкі құрылымдарын қабатқабат етіп көрсететін әдіс (мысалы, КТ –
компьютерлік
томография).
Компьютерлік
томографияның негізін қалаған — Годфри
Хаунсфилд (Ұлыбритания) және Аллан Кормак
(ОАР/АҚШ). Томографияда адам денесін әртүрлі
бұрыштан рентген сәулесімен "кесіп" өтетіндей етіп
суретке түсіреді.
Осы жерде дербес туындылар: Сәулелердің дене
арқылы өту жылдамдығын немесе сіңірілуін
модельдеуде, Қабаттар арасындағы өзгерістерді
есептегенде, Есептеу алгоритмдерінде (мысалы,
суретті қалпына келтіру үшін Фурье түрлендірумен
бірге
қолданылатын
Рэдон
түрлендіруінде)
пайдаланылады.
Годфри Хаунсфилд
(Ұлыбритания)
Аллан Кормак
(ОАР/АҚШ).
Компьютерлік томографтың прототипі

11.

Инженерлік есептеулердегі рөлі
Серпімділік теориясында деформациялар мен күштер арасындағы байланыс қарастырылады.
Беріктік есептеулері құрылымдардың жүктемеге төзімділігін анықтайды. Аэродинамикалық
модельдеу ұшақтардың және басқа да нысандардың ауа ағынындағы қозғалысын зерттейді.

12.

Экономика мен қаржыдағы қолданулар
Қаржылық модельдеу теңдеулері активтердің
бағасын
анықтауға
көмектеседі.
Нарық
динамикасын
болжау
үшін
әртүрлі
математикалық
әдістер
қолданылады.
Тәуекелдерді бағалау математикасы қаржылық
шешімдер қабылдауға негіз болады.

13.

Заманауи есептеу технологиялары
технологиялары
Сандық модельдеу әдістеріЗаманауи
дербесесептеу
туынды
теңдеулерін шешуге мүмкіндік береді.
Сандық
модельдеу әдістері дербес
туынды теңдеулерін
мүмкіндік
береді.
Суперкомпьютерлердегі
Суперкомпьютерлердегі
есептеулер
күрделішешуге
есептерді
жылдам
шешуге
көмектеседі.
есептеулер күрделі есептерді жылдам шешуге көмектеседі. Жасанды интеллект ДТТ-ді шешуде және
Жасанды интеллект ДТТ-ді
шешуде
және
модельдеуде
жаңа
мүмкіндіктер
ашады.
модельдеуде жаңа мүмкіндіктер ашады.

14.

Геофизика мен экологиядағы қолданулар
Климат өзгерісінің математикалық модельдері температураның өзгеруін және басқа да
климаттық факторларды болжауға көмектеседі. Судың таралу процестерін зерттеу үшін
гидродинамикалық теңдеулер қолданылады. Табиғи апаттарды болжау математикалық

15.

Қорытынды
Дербес туынды теңдеулері ғылым мен технологияларды
дамытуда маңызды рөл атқарады. Олардың қолданылуы
арқылы күрделі мәселелерді шешуге және болашақты
болжауға болады. Бұл саладағы зерттеулер әлі де көптеген