Similar presentations:
XX ғасырдағы математиканың дамуының өзіндік ерекшеліктері
1. XX ғасырдағы математиканың дамуының өзіндік ерекшеліктері
2. Жоспар
• XX ғасырдағы математиканың дамуының өзіндікерекшеліктері
• Орта Азия мен Қазақстан өңірінен шыққан ғалымдар
• Логикалық есептер
• Құнды мәліметтер
• Қытай халқындағы санақ
3.
4.
Бұл жерге келмейді ешкім ермекүшін,
Есеп – қисап, сан – цифр термек
үшін.
Көрсетіп есептердің жолын қалай,
Келдім мен оларды айтып бермек
үшін
5.
Сергіту сәті: Саусақтармен жасалатынайлалы әрекет.
Қол саусақтарын тек санау үшін ғана емес,
сонымен бірге көбейту үшін де пайдалнуға
болады. Осы айлалы әрекетті 9-ға көбейтуге
қолданып көр. Қолдарыңды алдыңа қойда, сол
жақтан оңға қарай санай баста. Қайсыбір
санды тоғызға көбейту үшін тиісті саусақты
бүк. Мысалы, 7-ні 9-ға көбейту үшін жетінші
саусағыңды бүк. Енді сол жақта 6 саусақ және
оң жақта 3 саусақ қалды, демек, жауабы 63
болады.
6.
7.
XX ғасырдағыматематиканың
дамуының
өзіндік
ерекшеліктері
Орта Азия
мен
Қазақстан
өңірінен
шыққан
ғалымдар
Логикалық
есептер
10
10
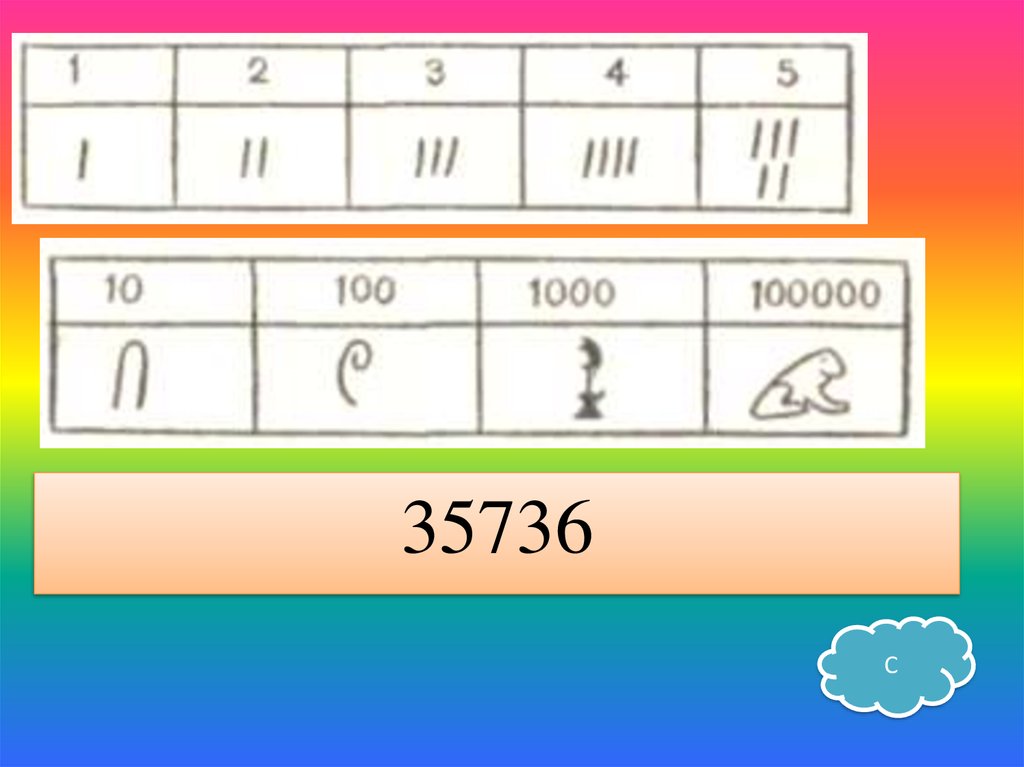
10
20
20
20
30
Құнды
мәліметтер
10
20
30
30
40
30
40
40
50
40
60
50
50
70
50
8.
1. Қай жылдан бастап КСРО ҒАҚазақ бөлімшесінің математика
және механика секторы маңызды
рөль атқарды?
9.
1945 жылдан10.
2. XX гасырдың 20-30 ж. жаңа типтегі жалпыбілім беретін мектептерде математика арнайы
оқытылды және XX ғасырдың 30-40 жылдары
қандай жаңа оқу орындарында алғашқы қазақ
математиктері кандидаттық диссертациялар
қорғады (И. Ақбергенов, Б.М. Оразбаев, О.А.
Жәутіков, т.б.)?
11. ((ҚазПИ (қазіргі ҚазҰПУ). ҚазМУ (қазіргі ҚазҰУ). ҚазПТИ (қазіргі ҚазҰТУ))
12.
3. Көрнекті Ресей математигі жәнемеханигі … жасаған орнықтылық
теориясы Қазақстан
математиктерінің зерттеу пәніне
айналды?
13.
А.М.Ляпунов (1857-1918)14.
4. Қазақстан математиктерінің үлкен бір тобыдербес туындылы теңдеулер мен математика
мен физиканың әр түрлі есептерін белсенді
түрде зерттеді?
15.
Е. Ким, М. Өтелбаев, Т. Қалменов, С. Харин, т.б.16.
5. Алгебра, сандар теориясы жәнематематика, логика мэселелерін
дамытуда кімдер белсенді
зерттеулер жүргізілді?
17.
А. Тайманов, Оразбаев18.
1. Әл-Хорезмидің толық есімі19.
Әбу Абдулла (немесе ӘбуЖафар) Мұхаммед ибн Мұса
әл-Хорезми)
20.
2.12 жасында Нишапурдағы медресенин
шәкірті аталған қай ғалым?
21.
Омар ибн Ибрахим Нишапури22.
3. 1312 ж. “Китаб әл-Алаийя” (“Жоғарыматематика кітабы”) трактатын жазған кім?
23.
Жамал Әд-Дин Әаид атТүркістани24.
4. Ғылым мен діннің шекарасын ажыратудықарастырды, білім таратудың жақтаушысы, ғылым
мен ағартушылық халықтарды дөрекіліктен,
кедейліктен босатады деп ойлады, ол оқыту мен
тәрбие жұмысын ізгілік ойлау қасиеттерін
қалыптастыру - бақытқа жету амалы деп санады. Ол
нашар мінез-құлықты тәрбиелеу арқылы түзетуге
болады деді. Ол кім?
25.
Әбу Рейхан Мухаммед ибнАхмед әл-Бируни
26.
5. Ғаббас Әл-Жауһаридің Дамаскіде өтілгенбақылаулар негізінде жазылған еңбегі
27.
"Мамунның астрономиялық кестелері"28.
1. Әл-Каши (XV ғ)есебі.Жұмысшыға бір айға төленетін
еңбек ақы, демек отыз күнге, он
динар мен көйлек. Жұмысшы үш
күн жұмыс істеді, және жұмысы
үшін көйлек төледі. Көйлектің
құны қанша?
29.
10/9 динарС
30.
2. Бұл отбасында 12 бала. Анасыбалдарына 70 алма әкелді . Анасы әкелген
алмалардың жартысын қыздарына бөліп
бергенде ,әрқайсысы бірдей алма алды,
қалған алмалардаң жартысын ұлдарына
бөліп берді,онда да ұлдарына тепе-тең
алмадан тиді.Бірақ әрбір ер бала әрбір
қыздан екі алма артық алды. Сонда бұл
отбасында неше ұл,неше қыз бар.
31.
7 қыз, 5 ұлС
32. 3. «Қызықты сандар» Үш тақтада бір-біріне ұқсас жұмбақ беріліп отыр. Шешулері де бір өңкей қызық сандар. Сонымен сұрау
белгілерінің орнына қажеттідеген сандарды дұрыс тауып жазыңыздар.
33.
45, 27, 6334.
4. Ежелгі Қытай есебіа Сунь-цзы (III-IV ғғ. ) есебі
Заттар бар, бірақ олардың
саны белгісіз. Егер оларды
үштік деп санаса, онда екі
қалдық, егер оларды
бестікпен санаса 3 қалдық ;
егер оларды жетілікпен
санаса 2 қалдық қалады.
Қанша зат бар екені
сұралады?
35.
23С
36.
5. Цифрограмма«Компьютер»
Төмендегі цифрлардың тілін тауып,
сөйлеткенде ежелгі грек ойшылы әрі математигі
Пифагордың сандар туралы айтқан тұжырымын
оқуға болады.
37.
АӘ
Б
В
Г
Ғ
Д
Е
Е
Ж
З
И
Й
К
Қ
Л
М
Н
Ң
О
Ө
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
П
Р
С
Т
У
Ұ
Ү
Ф
Х
Һ
Ц
Ч
Ш
Щ
Ъ
Ы
І
Ь
Э
Ю
Я
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
38.
«Бар болмыстың бастамасы сан»С
39.
6. Ұлу ағаштың басына шығуға күніне 5м жоғары көтеріледі де, түнде 3м сырғанап
төмен түседі. Ағаштың биіктігі 25м болса,
ұлу ағаштың басына неше күнде жетеді?
40.
Ұлу тәулігіне 2 метрге (5-3=2) көтеріледі. 9тәулікте 18 м, 10 – тәулщікте 18+5-3= 20
метрге, ал 11 күні кешке 20+5=25метрге
көтеріледі.
С
41.
7. Сізде 500 тенге бар. Сіз базардан 100 басқылып тауық, қораз, балапан алуыңыз керек.
Қораз 50 тенге, тауық 10 тенге, балапан 1
тенге. Осы 3-нен 100 бас алуыңыз керек. 500
тенгеге қанша қораз, қанша тауық, қанша
балапан алу керек?
42.
500 теңгеге 60 балапан, 39 тауық, 1 қоразаласыз. Есептеп қараңыз!
60 балапан 60 теңге, 39 тауық 390 теңге, 1
қораз 50 теңге.
60 балапан+39 тауық+1 қораз=100 бас
60 теңге+390теңге+50теңге=500 теңге
С
43.
1. Ең алғашқы әйел математик44. Софья Васильевна Ковалевская 1850жылы 3 қаңтарда Мәске қаласында дүниеге келген.
С45.
2. Мысырдың иероглифтікнумерациясы?
46.
35736С
47. 3. Бұл кім?
48.
Математика бойынша әлемдегі ең танымалФилдс сыйлығын 78 жылдық тарихында
алғаш рет әйел адам еншіледі. Бұл адамның
есімі – Мириам Мирзахани. Иранда туған. 2008
жылдан бері Стэнфорд университетінде (АҚШ,
Калифорния) сабақ береді. Профессор.
“Филдс” 4 жылда бір рет 40 жасқа дейінгі
ғалымдарға берілетін математика ғылымының ең
жоғарғы сыйлығы. Бұған дейін оны тек ер
адамдар алып келген.
Жеңімпаз өзінің бұл жеңісі жас ғалым қыздарды
қуаттандырып, ғылымға деген қызығушылығын
арттыра түседі деп сенім артатынын айтты.
Филдс сыйлығы математика саласында Нобель
сыйлығымен пара-пар.
С
49. 4. Бұл жерде қандай жаналық болып отыр?
50.
Әлемдегі ең танымал сөзжұмбақ түрлерініңбірі судоку болып есептеледі. Ол санмен байланысты
жапондық жұмбақ. Аталған ойынның принциптері аса
қиын емес, сондықтан көптеген әуесқойлар
жұмбақтың өз нұсқасын жасап шығаруға тырысып
жатады. 2012 жылы фин математигі Арто Инкала да
өзінің нұсқасын жасап, оның «ең қиын судоку» екенін
мәлімдеген болатын.
Британдық «The Telegraph» газетінің хабарлауынша,
егер судокудің кеңінен таралған ең қарапайым
нұсқаларын қиындық межелігі бойынша «1» деп
белгілеп, қиындарын «5» деп белгілесе, фин
математигі ұсынған нұсқа «11»-ге тең келеді-міс.
С
51.
5. Әлемдегі 7 қиын есептерді атаңыз?52.
1) Кук қиындығы2) Риман гипотезасы
3) Берч және Свиннертон-Дайер
гипотезасы
4) Ходж гипотезасы
5) Навье-Стокс теңдеуі
6) Янг-Миллс теңдеуі
7) Д’Аламбер-Эйлер парадоксы
53.
1) Кук қиындығыБір де бір есеп шешімінің дұрыстығын тексеру, сол шешімді
табуға кеткен уақыттан ұзағырақ бола алады ма? Бұл логикалық
есеп криптография (ақпаратты шифрлау) негіздерін “адам
танымастай” өзгертер еді.
2) Риман гипотезасы
2, 3, 5, 7, т.т сияқты өзіне ғана бөлінетін жай сандар бар. Қанша
жай сан бар екені белгісіз. Шешімі бар екенін және олардың
таралу заңдылықтарын анықтауға болатынын Риман болжаған.
Кімде кім тапса – криптографияға үлкен қызмет болар еді.
3) Берч және Свиннертон-Дайер гипотезасы
Қиындық – дәрежелі үш белгісізі бар теңдеуді( x2 + y2 =
z2 типтес) шешумен байланысты. Күрделілігі әр түрлі
теңдеулерге жарайтын тәсіл табу керек. Евклид x2 + y2 =
z2 теңдеуінің шешімін толығымен түсіндіріп кеткен. Бірақ,
күрделі теңдеулерді шешуге өте қиын.
54.
4) Ходж гипотезасыКүрделі объекттердің формасын зерттеу амалдарын
математиктер ХХ ғасырда тапқан. Гипотезаның
негізгі идеясы объекттің орнына қарапайым
“кірпіштерді” қолдану. Ол “кірпіштер” өзара
жабыстырылған және объекттің көшірмесіндей.
Объект құрастыруға болатынын және бұның әр
уақытта мүмкін екенін дәлелдеу керек.
5) Навье-Стокс теңдеуі
Ұшақта отырып есіңізге түсіріңіз. Теңдеу ұшақты
ауада “қалқытатын” ауа ағындарын сипаттайды.
Қазіргі күні жорамалдап шығарады, жорамал
формулалармен. Дәл теңдеуді анықтап, әрдайым
дұрыс және үш-өлшемді кеңістікте (трехмерое
пространство) шешімі бар теңдеулер барын
дәлелдеу керек.
55.
6) Янг-Миллс теңдеуіФизика әлемінде гипотеза бар: егер элементар бөлшектерде
масса болса, онда оның төменгі шегі де болады. Қандай екені
– белгісіз. Бұл ең қиын есептердің бірі. Шешімін табу үшін,
табиғаттағы барлық әрекеттесу күштерін байланыстыратын
“барлық теория” теңдеуін ойлап табу керек. Тапқан адам,
сөзсіз Нобель сыйлығын алар еді.
7) Д’Аламбер-Эйлер парадоксы
Бұл парадокс – гидродинамика қағидасы, кез-келген шектеулі
формалы дененің шексіз сығылмайтын, тұтқырлықсыз, әрі
құйынтуғызбайтын және жылдамдық үзілу
жазықтықтарынсыз сұйықтықтың ішіндегі бірқалыпты және
сызықтық қозғалысы кезінде сұйықтықтың дене қозғалысына
қорытынды үйкеліс күші нөлге тең (1744-жылы Ж.
Д’Аламбер, 1745 жылы Л. Эйлер айтқан). Адиабатты
қозғалатын идеал газ үшін дәлелденген. Физикалық үйкеліс
күшінің жоқтығы жоғарыда айтылған жағдайларда сұйықтық
не газ ағындары қозғалыстағы дененің арт жағында
С
тұйықталуымен түсіндіріледі, жалпы сұйқтық арт жаққа әсер
ете отырып, алдыңғы жаққа түсірілетін күшті теңестіреді.
56.
Леонард Пизанскийдің есебі.(итальян математигі Л.
Пизанский (1180-1240) лақап
аты Фибоначчи).
30 құс30 тиын, қарғалар 3
тиын,көгершіндер – екі және
жұп торғайларбір тиыннан; әр
құс түрлері қанша?.
57.
Қиындықтан сірә да біз қашпаймыз.Алғырлықпен тапқырлықты ұштаймыз.
Қиялдарға самғап ұшқан құстаймыз.
Шегінбейміз жеңістерге бастаймыз - дей
отырып, жеңімпазды анықтайық.
Көңіл бөліп бұл кешке,
Келгендерге көп рахмет.
Шын сезінген көрерменге,
Мың рахмет, мың рахмет!
58.
Қытай халқында1 саны – «жаңа туған нәресте»
2 саны – қосылу, толықтыру символы
3 саны - Көптеген елдердегідей бұл да қасиетті сан болып есептелінеді.
Жарықтың үш көзі – Жұлдыз, Күн мен Ай,
Үш бастау – Аспан, Жер, Адам
4 саны - Қытайлардың үрейін ұшыратын 4 саны қасірет саны болып саналады.
Өйткені ол «өлім» дегенді білдіреді.
5 саны – аса құрметті сан. 5 саны ауқатты, күшті, белсенді де сабырлы және
биіктен көрінер сан.
6 саны – «байлық» дегенді білдіріп, құрмет тұтатын сандар қатарына кіреді.
7 саны – 7 ге ерекше көңіл бөлінетін себебі, ол өміріміздің негізгі циклы –
аптаны, сол аптаның ішіндегі 7 күнді білдіреді.
8 саны - Қытайлардың ең сүйікті саны. «Гүлдену» дегенді білдіреді. Сондықтан
«арты гүлдеуге әкелсін» деген ниетпен 2008 жылы Бейжин Олимпиадасының
ашылу уақыты 8-ші айдың 8-ші жұлдызы, сағат 8-ден 8 минут 8 секунд өткен
























































 mathematics
mathematics








