урок 11Биноминальное и геометрическое распределение. Свойства. Примеры (4)

1.

Биномиальное и
геометрическое
распределения.

2.

Фундаментальные условия схемы
независимых испытаний Бернулли.
1. Опыты проходят в одних и тех же неизменных условиях.
2. Каждый опыт приводит к одному из двух взаимно
исключающих исходов, которые условно называют «УСПЕХ» и
«НЕУДАЧА» - это взаимно несовместные и противоположные
события.
3. Вероятность «успеха» p остается постоянной от испытания к
испытанию. Вероятность «неудачи» – q.
4. Все испытания независимы.

3.

Биноминальное распределение
1. Опыты проходят в одних и тех же неизменных условиях.
2. Каждый опыт приводит к одному из двух взаимно
исключающих исходов, которые условно называют «УСПЕХ» и
«НЕУДАЧА» - это взаимно несовместные и противоположные
события.
3. Вероятность «успеха» p остается постоянной от испытания к
испытанию. Вероятность «неудачи» – q.
4. Все испытания независимы.
5. Число опытов ограниченное, т.е. фиксированное число n.
6. X — это число «успехов» в n испытаниях

4.

Формула Бернулли
Вероятность того, что в n независимых испытаниях «успех»
наступит ровно m раз, равна
Pn (m) C p q
m
n
m
n m
где p – вероятность «успеха» в каждом испытании, а q = 1 – p,
и m = 0, 1, 2, …, n.
О случайной величине – число «успехов» в n независимых
испытаниях – говорят, что она имеет биномиальное
распределение с параметрами n и p.

5.

Задача на биномиальное распределение
ПРИМЕР 1. Монету подбрасывают 10 раз подряд. Случайная величина X
равна числу испытаний, в которых на монете выпал орёл.
Найдём закон распределения этой величины.
Очевидно, что возможные значения X — это целые числа от 0 до 10.
Чтобы найти вероятности этих значений, рассмотрим наши десять опытов
как серию из 10 испытаний Бернулли. Если считать выпадение орла успехом,
то X — это число успехов в 10 испытаниях Бернулли.
Получается, что вероятность события {X = k} для любого значения k от 0 до
10 можно посчитать по формуле Бернулли:

6.

Подставить в эту формулу значения k = 0, 1, … , 10 и запишем полученные
значения в таблицу

7.

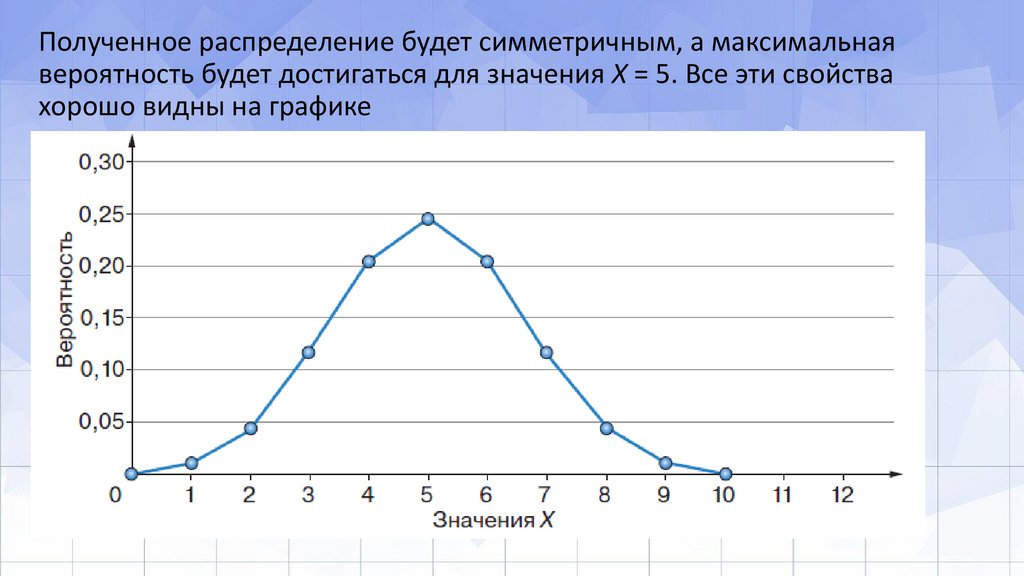
Полученное распределение будет симметричным, а максимальная
вероятность будет достигаться для значения X = 5. Все эти свойства
хорошо видны на графике

8.

9.

Вычислим эти вероятности для k = 0, 1, … , 8
Вероятности двух последних значений получились такими маленькими, что
пришлось записывать их в стандартном виде, с умножением на десять в
отрицательной степени.

10.

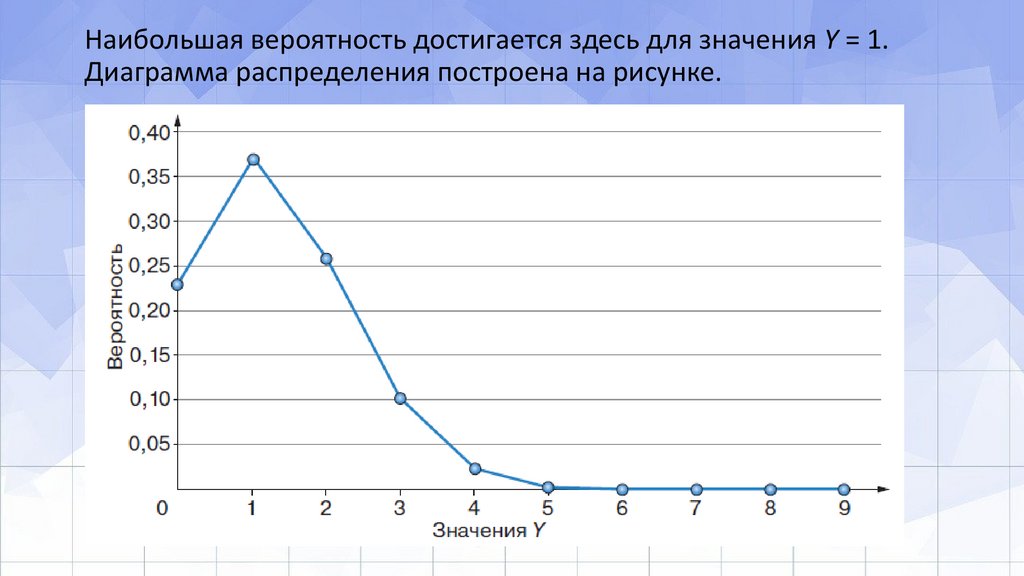
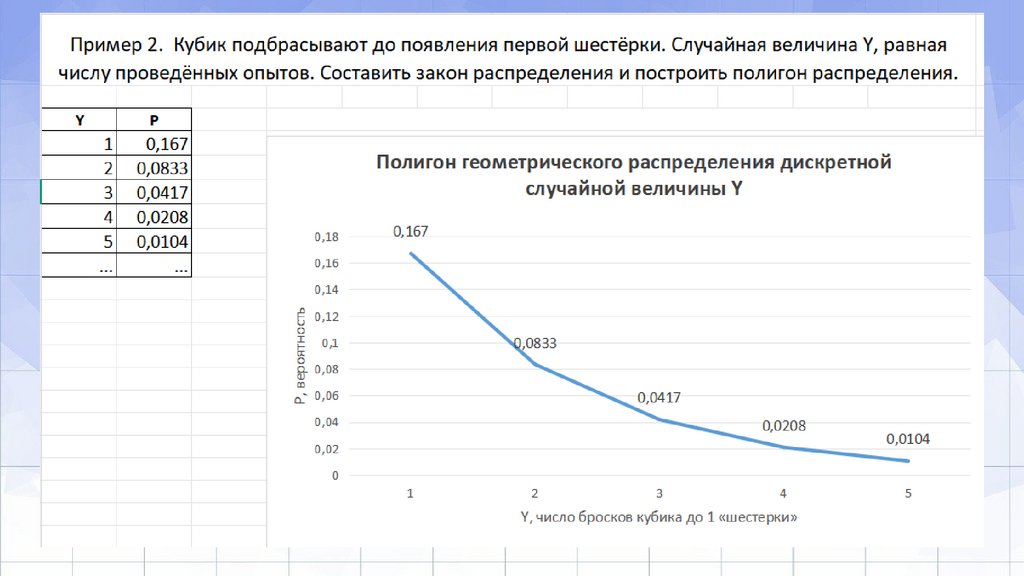
Наибольшая вероятность достигается здесь для значения Y = 1.
Диаграмма распределения построена на рисунке.

11.

12.

Задача 1
В магазин поступила обувь с двух фабрик в соотношении
2:3. Куплено 4 пары обуви. Найти закон распределения
числа купленных пар обуви, изготовленной первой
фабрикой. Найти математическое ожидание и среднее
квадратическое отклонение этой случайной величины.

13.

По условию поступила обувь с двух фабрик в соотношении 2:3.
Вероятность того, что случайно выбранная пара обуви изготовлена первой фабрикой,
p = 2 / (2 + 3) = 0,4,
изготовлена не первой фабрикой q = 1 – p = 0,6.
x1 = 0, событие A1 – ни одна пара не изготовлена 1-й фабрикой.
P(X = 0) = P4 (0)=C40 p0 q 4 – 0= 1∙0.40∙0.64=0,1296
x2= 1, событие A2 – одна пара изготовлена 1-й фабрикой
P(X = 1) =P4 (1)=C41 p1 q 4 – 1= 4∙0.41∙0.63= 0,3456
x3 = 2, событие A3 – две пары изготовлены 1-й фабрикой
P(X = 2) =P4 (2)=C42 p2 q 4 – 2 =6∙0.42∙0.62 = 0,3456
x4 = 3, событие A4 – 3 пары изготовлены 1-й фабрикой
P(X = 3) = P4 (3)= C43 p3 q 4 – 3 = 4∙0.43∙0.61= = 0,1536
x5= 4, событие A5 – 4 пары изготовлены 1-й фабрикой
P(X = 4) = P4 (4)= C44p4 q 4 – 4 = 1∙0.44∙0.60 = = 0,0256

14.

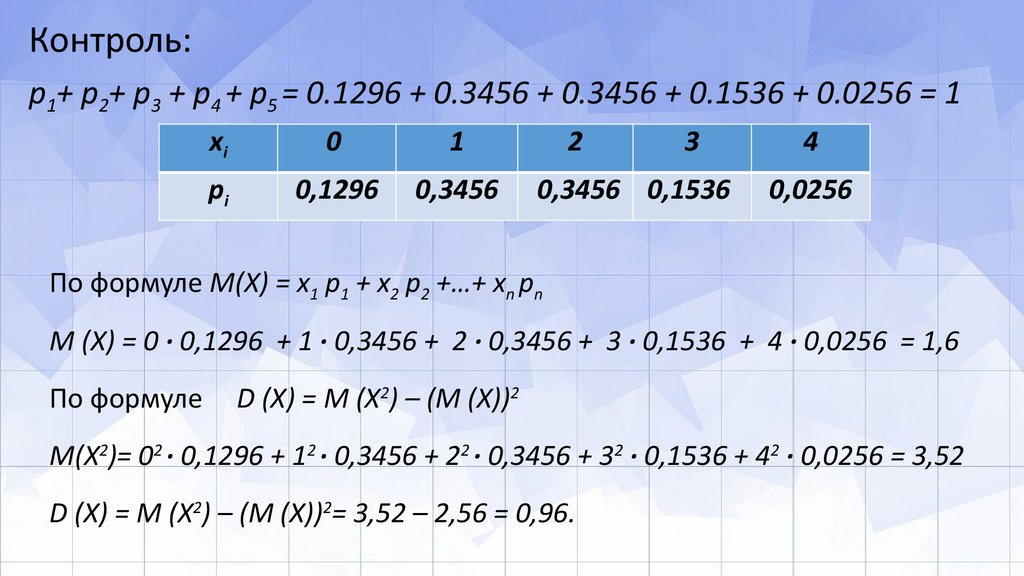
Контроль:
p1+ p2+ p3 + p4 + p5 = 0.1296 + 0.3456 + 0.3456 + 0.1536 + 0.0256 = 1
xi
0
1
pi
0,1296
0,3456
2
3
0,3456 0,1536
4
0,0256
По формуле М(Х) = x1 p1 + x2 p2 +…+ xn pn
М (Х) = 0 · 0,1296 + 1 · 0,3456 + 2 · 0,3456 + 3 · 0,1536 + 4 · 0,0256 = 1,6
По формуле
D (X) = M (X2) – (М (Х))2
M(X2)= 02 · 0,1296 + 12 · 0,3456 + 22 · 0,3456 + 32 · 0,1536 + 42 · 0,0256 = 3,52
D (X) = M (X2) – (М (Х))2= 3,52 – 2,56 = 0,96.

15.

Свойства биномиального распределения.
P ( Х m) C p q
m
n
m
n m
Математическое ожидание биномиального
распределения M(X) = np.
Дисперсия равна: D(X) = npq.

16.

17.

18.

Задача № 3
Стрелок может поразить мишень с вероятностью 0,9. Составить
закон распределения числа попаданий в цель при четырех выстрелах.
Найти среднее число попаданий при четырех выстрелах и разброс
значений числа попаданий для данного стрелка при четырех выстрелах.
Дано: Испытание – четыре выстрела по мишени.
Событие А – мишень поражена
Р(А) = 0,9
Случайная величина X – число попаданий при
четырех выстрелах,
Найти: а) X, б) M(X), в) D(X).

19.

Решение:
Случайная величина X - число попаданий в цель при четырех выстрелах – может
принимать значения
0,1, 2, 3, 4
Соответствующие вероятности найдем по формуле Бернулли: P(X = m) = Pn(m) =
Cnm p m q n – m.
Число испытаний n равно 4
Вероятность «успеха» - это вероятность того, что стрелок попадет в цель - 0,9
Число «успехов» равно m, и меняется в соответствии со значениями случайной
величины.

20.

x1 = 0, событие A0 – ни одного попадание при четырех выстрелах.
P(X = 0) = P4 (0)= C40 p0 q 4 – 0 = 1∙0.90∙0.14 = 0,0001
x2= 1, событие A1 – одно попадание при четырех выстрелах.
P(X = 1) = P4 (1)= C41 p1 q 4 – 1 = 4∙0.91∙0.13 = 0.0036
x3 = 2, событие A2 – два попадания при четырех выстрелах.
P(X = 2) = P4 (2)= C42 p2 q 4 – 2 = 6∙0.92∙0.12 = 0,0486
x4 = 3, событие A3 – три попадания при четырех выстрелах.
P(X = 3) = P4 (3)= C43 p3 q 4 – 3 = 4∙0.93∙0.11 = 0.2916
x5= 4, событие A4 – четыре попадания при четырех выстрелах.
P(X = 4) = P4 (4)= C44p4 q 4 – 4 = 4∙0.94∙0.10 = 0,6561

21.

Искомый закон распределения имеет вид:
Xi 0
1
2
3
4
Pi 0.0001 0.0036 0.0486 0.2916 0.6561
Найдем среднее число попаданий при четырех выстрелах.
По свойству биномиального распределения математическое
ожидание биномиального распределения равно
произведению числа испытаний на вероятность «успеха» в
каждом испытании: M(X) = np.
Тогда M(X) = np = 4∙0,9 = 3,6 – среднее число попаданий при
четырех выстрелах.

22.

23.

Геометрическое распределение
С испытаниями Бернулли связано ещё одно распределение вероятностей,
которое называется геометрическим.
Рассмотрим серию испытаний Бернулли до первого успеха.
Пусть X — это число опытов, которое потребовалось при этом провести.
Тогда X — дискретная случайная величина с бесконечным множеством
возможных значений.

24.

Геометрическое распределение
1. Опыты проходят в одних и тех же неизменных условиях.
2. Каждый опыт приводит к одному из двух взаимно исключающих
исходов, которые условно называют «УСПЕХ» и «НЕУДАЧА» - это
взаимно несовместные и противоположные события.
3. Вероятность «успеха» p остается постоянной от испытания к
испытанию. Вероятность «неудачи» – q.
4. Все испытания независимы.
5. Опыты проводятся до первого успеха. Число опытов
неограниченное.
6. X — случайная величина, равная количеству проведенных попыток
(или может быть число неудачных попыток до первого «успеха»)

25.

26.

Она и даёт нам искомое распределение вероятностей
Таблица продолжается вправо до бесконечности. Тем не менее основное
свойство закона распределения всё равно сохраняется: сумма всех
вероятностей равна 1. Мы уже доказали это, когда изучали испытания
Бернулли:

27.

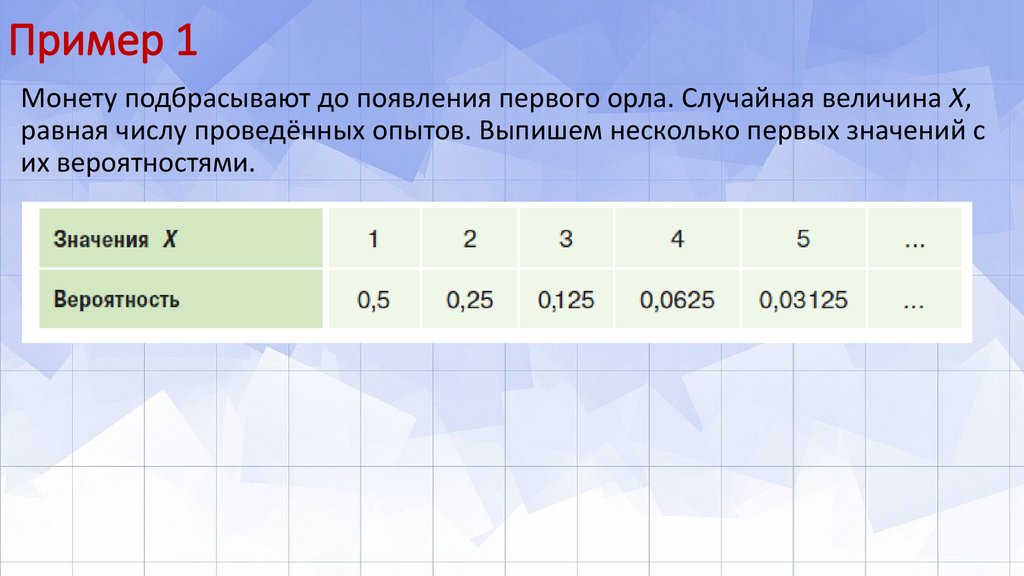
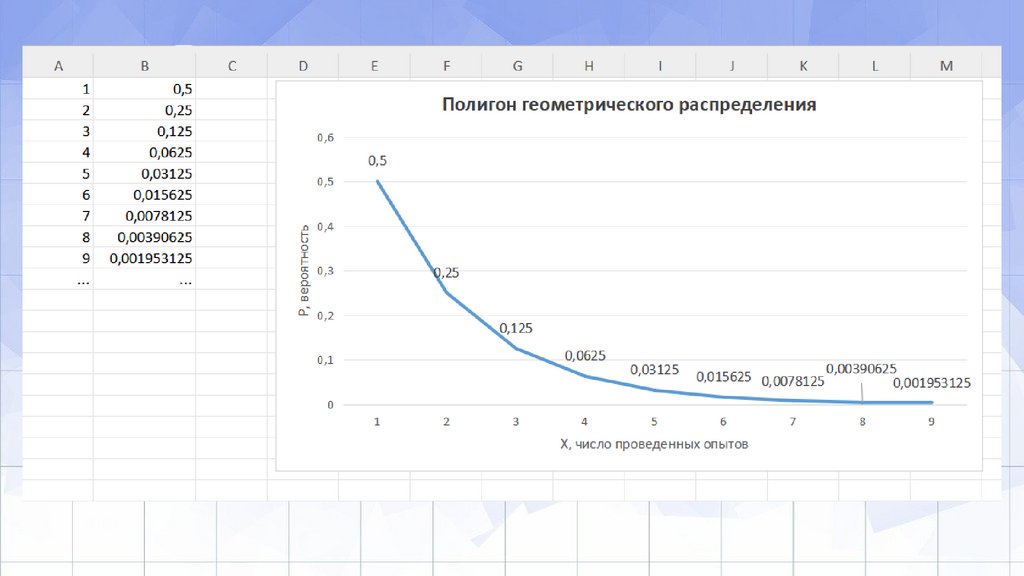
Пример 1
Монету подбрасывают до появления первого орла. Случайная величина X,
равная числу проведённых опытов. Выпишем несколько первых значений с
их вероятностями.

28.

29.

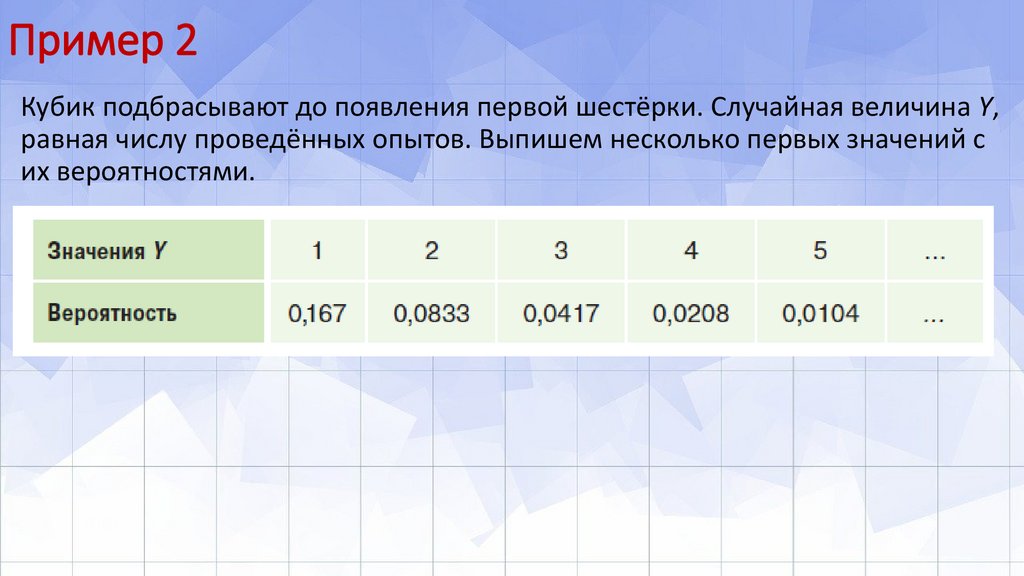
Пример 2
Кубик подбрасывают до появления первой шестёрки. Случайная величина Y,
равная числу проведённых опытов. Выпишем несколько первых значений с
их вероятностями.

30.

31.

32.

33.

Задание 1

34.

Задание 2

35.

Задание 3
Студент сдаёт зачёт по теории вероятностей до тех пор, пока не решит какуюнибудь задачу. Вероятность решения любой задачи этим студентом равна
0,2. Случайная величина Z равна числу задач, которые он получит, пока не .
Составить закон распределения. Построить полигон распределения,
составить функцию распределения и построить ее график

36.

Домашнее задание:
1. В партии 8% нестандартных деталей. Из неё наугад отбирают
5 деталей. Случайная величина X равна числу нестандартных
деталей среди отобранных. Найдите закон распределения
случайной величины X. Какое число нестандартных деталей в
этой выборке наиболее вероятно?
2. Профессор не хочет ставить положительную оценку студенту и
задаёт ему вопросы до тех пор, пока на очередном вопросе
студент не ошибётся. Вероятность правильного ответа на
любой вопрос составляет 0,9. Случайная величина X равна
числу вопросов, на которые правильно ответит студент перед
тем, как получит двойку. Найдите закон распределения
случайной величины X.