Метод функционала плотности

1. Метод функционала плотности

Презентацию подготовили студентки
группы СЭ-201 Шашлова Е.С. иЧушкина В.А.

2. Введение

Теория функционала плотности — метод
расчёта электронной структуры систем
многих частиц в квантовой физике и
квантовой химии. В частности,
применяется для расчёта электронной
структуры молекул и конденсированного
вещества. Является одним из наиболее
широко используемых и универсальных
методов в вычислительной физике и
компьютерной химии.

3. Метод функционала плотности (DFT)

Теоремы Хенберга—Кона
1. Существует взаимно однозначное соответствие между
электронной плотностью основного состояния
электронной подсистемы, находящейся во внешнем
потенциале атомных ядер, и самим потенциалом ядер.
2. Энергия электронной подсистемы, записанная как
функционал электронной плотности, имеет минимум,
равный энергии основного состояния.
В DFT методе волновая функция состоит из
одночастичных самосогласованных функций Φi.

4.

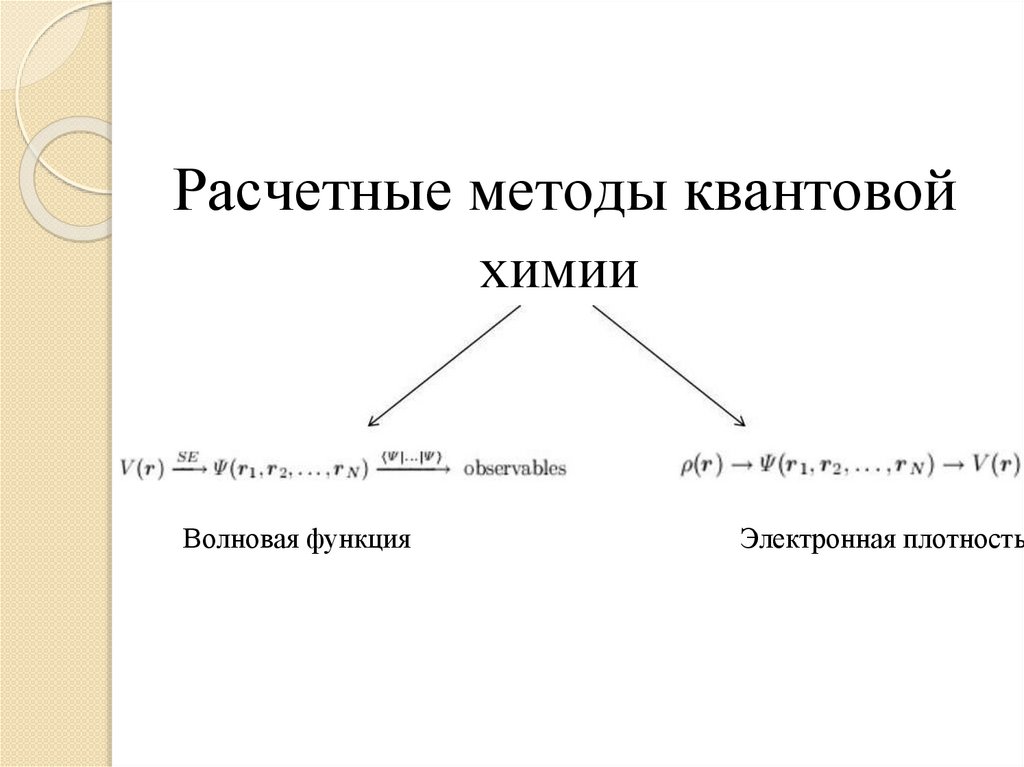
Расчетные методы квантовой
химии
Волновая функция
Электронная плотность

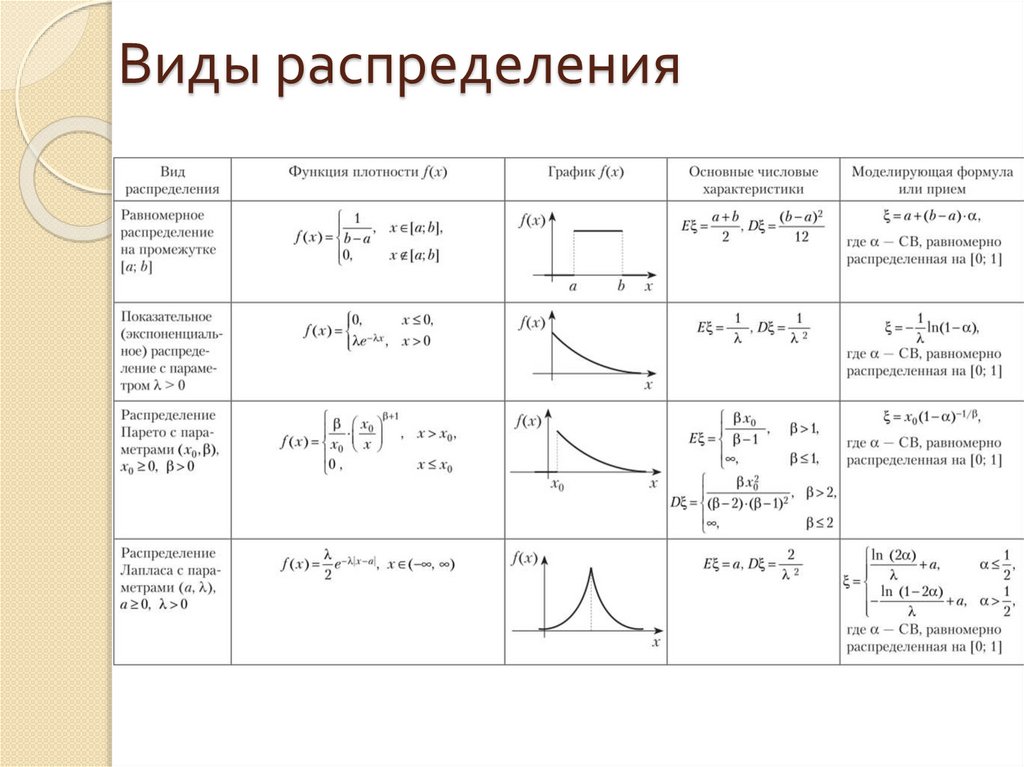
5. Виды распределения

6. Теоремы Хоэнберга-Кона

1) Электронная плотность основного
состояния однозначно соответствует
многоэлектронной волновой функции
основного состояния.
2) Полная энергия основного
состояния многоэлектронной системы
может быть рассчитана как функционал
электронной плотности:

7. В чем преимущества такого подхода ?

Энергия корреляции и выход за
рамки однодетерминантного
приближения
2) Электронная плотность зависит от З
переменных (а многоэлектронная
волновая функция — от 3N
переменных).
1)

8. Уравнения Кона-Шэма

Каждой системе взаимодействующих электронов,
Движущихся во внешнем поле V0(r), можно поставить в
соответствие “невзаимодействующую” систему с
локальным потенциалом Vs0(r), таким, что в основном
состоянии плотности p(r) и ps(r) для обоих систем будут
равны.

9. Приближения

Основная проблема, связанная с методом теории
функционала плотности заключается в том, что точные
аналитические выражения для функционалов обменной и
корреляционной энергии известны только для частного
случая газа свободных электронов.
Приближение локальной плотности (LDA)
Функционал, вычисляемый для некоторой точки пространства,
зависит только от плотности в этой точке:
Е XC [n] e XC (n)n(r )d 3 r
или для случая локальной спиновой
плотности Е XC [n] eXC (n , n )n(r )d 3r
Метод обобщённого градиентного приближения (GGA)
также является локальным, но, в отличие от метода локальной
плотности, учитывает градиент плотности в точке
рассмотрения:
Е XC [n] eXC (n , n , n , n )n(r )d 3r

10. LDA - Локальная аппроксимация плотности.

Энергию обменных корреляций можно представить в виде:
LDA
Exc
[ ] (r ) xc ( (r ))dr ,
xc ( (r )) x ( (r )) c ( (r )),
1/3
3 3 ((r ))
x ( (r ))
4
обменная энергия Дирака/Слэтера
Кулоновская часть корреляции получена из интерполяций
данных расчетов квантового Монте-Карло (Ceperly, Alder). В
настоящее время используется аппроксимация LDA, выполненная
в более точном приближении SWVN (Wilk, Vosko, Nussair;
Perdew, Wang), которое подразумевает добавку Слетеровской
обменной и кулоновской корреляций.

11. Схема приближения LDA

12. GGA –обобщенная градиентная аппроксимация

Результаты расчетов в приближении LDA не дают
достаточную точность для приложений.
Необходимо включать условия, которые явно
принимают во внимание пространственную
вариацию плотности. Это удается преодолеть в
рамках приближения обобщенного градиента
(GGA – аппроксимации обобщенного градиента).
Это приближение дает теории DFT хорошую
точность. Аппроксимации проводятся отдельно для
обменного и кулоновского взаимодействий.
Выражения для кулоновской части весьма сложны.
Наиболее часто используются аппроксимации:
LYP (Lee, Parr, Yang), PW91 (Perdew, Wang), P86
(Perdew).

13. Гибридные методы DFT

Методы DFT, в которые, так или иначе, включен хартри-фоковский
обменный член, называют гибридными методами. В этом случае
обменно-корреляционный функционал обычно записывается в виде
линейной комбинации,
где коэффициенты и сорг суть параметры функционала. Среди
гибридных наиболее часто используется трехпараметрический
функционал B3LYP.
обменная часть которого включает 20% хартри-фоковского обмена,
8% слэтеровского и 72% обмена по Беке, а корреляционная часть —
19% локального функционала VWN и 81% функционала LYP. В
другом трехпараметрическом гибридном функционале B3PW91
корреляционный вклад представлен функционалом PW91

14. Оценка обменно-корреляционной энергии

Оценка обменнокорреляционной энергии
Расчеты методами DFT выполняются по той же схеме,
что и расчеты методом Хатри-Фока, но требуют оценки
дополнительного члена,