Несовместные события. Формула сложения вероятностей

1.

Несовместные события.
Формула сложения
вероятностей.
Ст а т и с т и ка – это н ау ка ,
изу чающая процессы,
происходящие в обществе,
оценивающ ая и х
количественные и
качественные параметры.
Вероя́ т ность — степень
возможности наступления
некоторого события.
8 класс Вероятность и статистика
Урок 27

2. Несовместные события. Формула сложения вероятностей.

02.04.2025
К л а с с н а работа
Несовместные события.
Формула сложения
вероятностей.

3. Задачи урока:

- Рассмотреть примеры н а
использование понятия
несовместны е события.
- Науч иться решать задачи,
используя формулу
сложения вероятностей

4.

Готовимся к ВПР
6. Пассажиропоток — это количество пассажиров, которых перевозит
определённый вид транспорта за определённый промежуток времени (час,
сутки, месяц, год). Пассажиропотоком называют также количество пассажиров,
проходящих за определённый промежуток времени через транспортный узел
(вокзал, аэропорт, автостанцию). Особенностью пассажиропотоков является их
неравномерность и изменчивость: они зависят от времени, от направления и от
других факторов. Изменение пассажиропотока в зависимости от месяца или
времени года называется сезонностью пассажиропотока. На диаграмме показан
пассажиропоток аэропорта Храброво (Калининград) в 2019 году.
На сколько примерно человек снизился пассажиропоток в сентябре по
сравнению с августом? Чем можно объяснить рост пассажиропотока во второй
половине лета? Напишите несколько предложений, в которых обоснуйте своё
мнение по этому вопросу.
Ответ: ≈ 40000 человек

5.

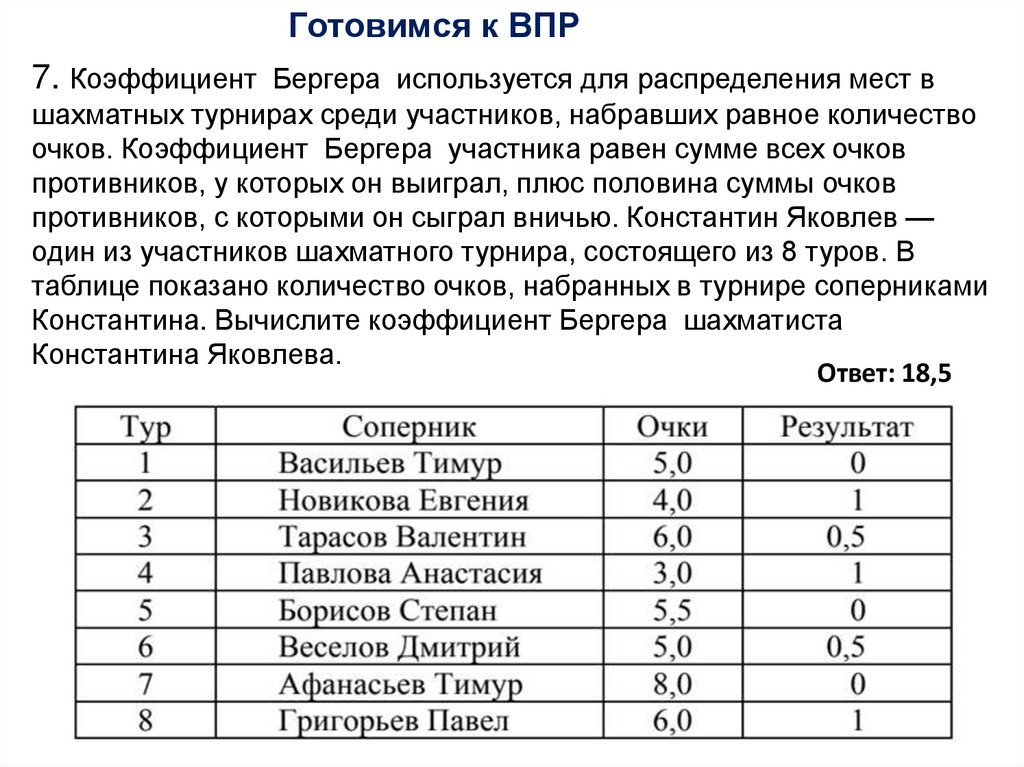
Готовимся к ВПР
7. Коэффициент Бергера используется для распределения мест в
шахматных турнирах среди участников, набравших равное количество
очков. Коэффициент Бергера участника равен сумме всех очков
противников, у которых он выиграл, плюс половина суммы очков
противников, с которыми он сыграл вничью. Константин Яковлев —
один из участников шахматного турнира, состоящего из 8 туров. В
таблице показано количество очков, набранных в турнире соперниками
Константина. Вычислите коэффициент Бергера шахматиста
Константина Яковлева.
Ответ: 18,5

6.

Повторение.
Отвечаем на вопросы
3 . Р(А ) + Р( А )=1 .

7.

Типы событий
• События А и В называют совместными,
если они могут произойти одновременно в
одном испытании.
• События A и B называются несовместными,
если они никогда не могут произойти в
результате одного испытания.

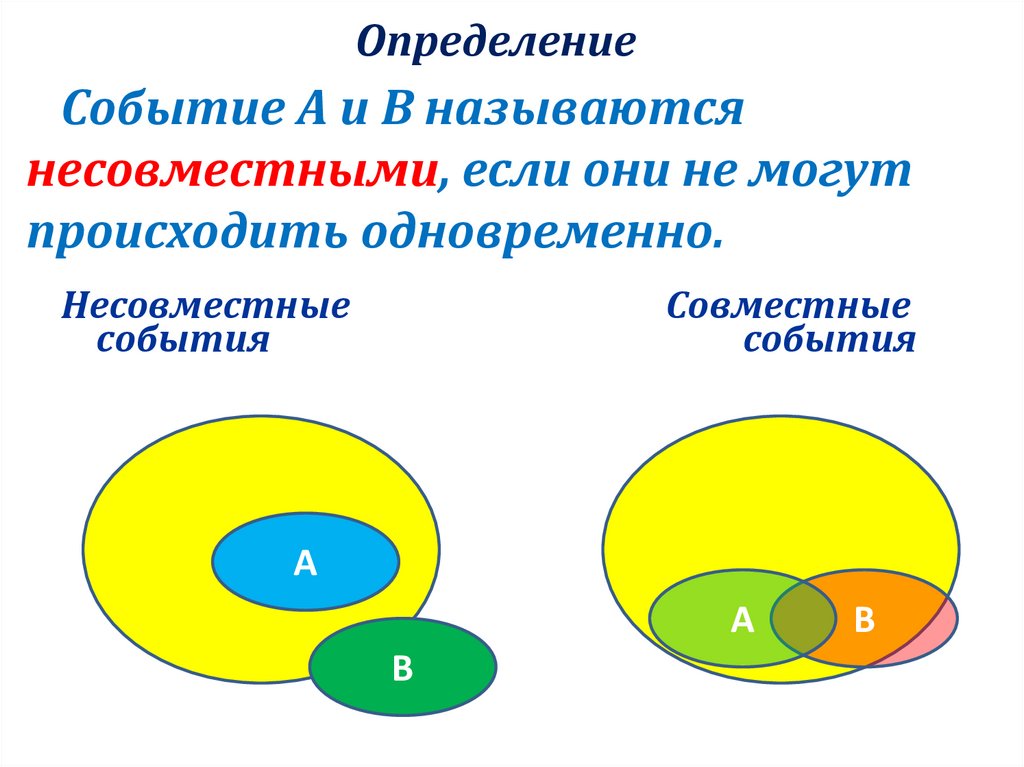
8. Определение

Событие А и В называются
несовместными, если они не могут
происходить одновременно.
Несовместные
события
Совместные
события
А
А
В
В

9.

Пример.
А – «идет дождь»,
В – «на небе нет ни облачка»
– несовместные.
Пример.
Коля и Саша играют в шашки.
А – «Коля проиграл»,
В – «Саша выиграл»,
С – «Витя наблюдал за игрой»
– совместные.

10. Теорема

Теорема сложения вероятностей несовместных событий
Если события А и В несовместны, то событие А+В
заключается в том, что должны наступить А или В, тогда +
заменяется словом «или».
Теорема: Вероятность появления одного из двух
несовместных событий, безразлично какого, равна сумме
вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
Вероятность наступления хотя бы одного из двух
несовместных событий равна сумме их вероятностей.
Если А и В несовместны,
то Р(А+В) = Р(А) + Р(В)
Доказательство:

11.

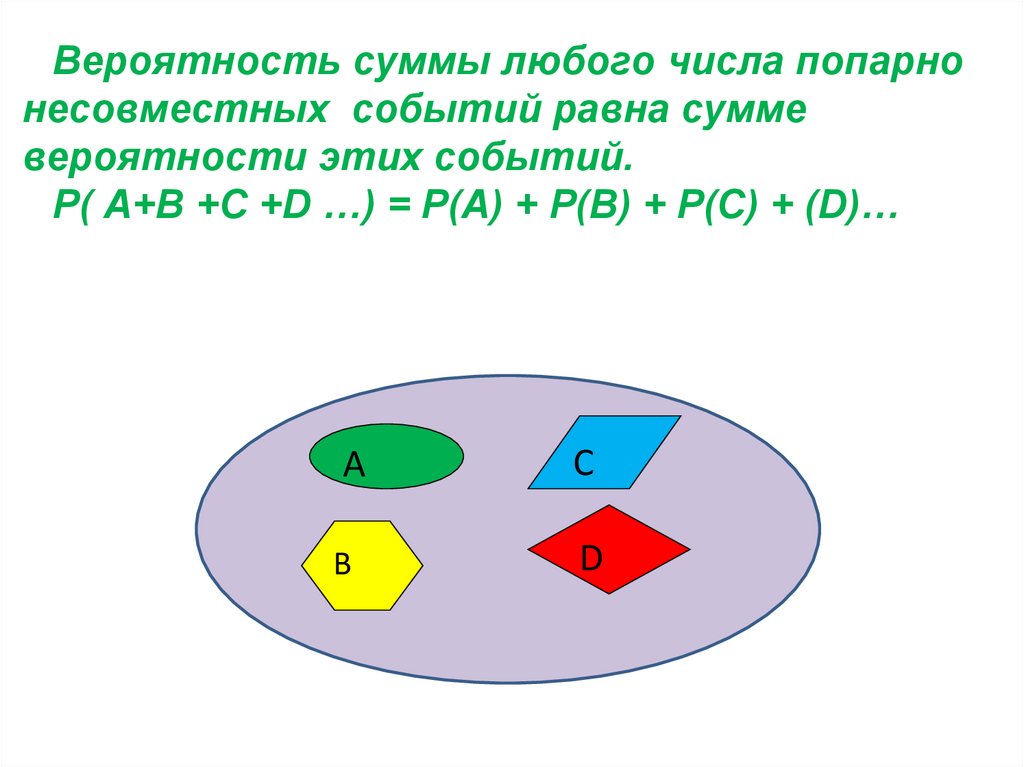
Вероятность суммы любого числа попарно
несовместных событий равна сумме
вероятности этих событий.
Р( А+В +С +D …) = Р(А) + Р(В) + Р(С) + (D)…
А
С
В
D

12. Решаем задачи. Выполняем упражнения

Пример 1:
В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти
вероятность появления цветного шара.
Решение:
Появление цветного шара означает появление либо красного,
либо синего шара.
Соб. А – появление красного шара. Вероятность появления соб.
А: Р(А)=10/30=1/3.
Соб. В – появление синего шара. Вероятность появления соб. В:
Р(В) = 5/30=1/6.
События А и В несовместны (появление шара одного цвета
исключает появление шара другого цвета), поэтому теорема
сложения применима. Искомая вероятность:
Р(А+В)= Р(А)+Р(В)= 1/3+1/6=1/2.

13. Теорема сложения вероятностей совместных событий.

Теорема: Вероятность появления хотя бы
одного из двух совместных событий равна
сумме вероятностей этих событий без
вероятности их совместного появления:
Р(А+В)=Р(А)+Р(В) – Р(АВ)
Частным случаем приведенной формулы является
формула сложения вероятностей для несовместных событий,
так как их совместное наступление есть невозможное
событие и P(AB)= 0 .
Для случая трех совместных событий формула имеет вид:
Р(A+ B+ C) = P( A)+ P( B)+ P( C) - P (АB) - P( AC) - P( BC) +
P( ABС).

14. Решаем задачи. Выполняем упражнения

Пример 2:
Вероятности попадания в цель при стрельбе первого и второго
орудий соответственно равны Р(А) =0,7 и Р(В) =0,8. Найти
вероятность попадания при одном залпе хотя бы одним из
орудий.
Решение:
Вероятность попадания в цель каждым из орудий не зависит от
результата стрельбы из другого орудия, поэтому события А
(попадание первого орудия) и В (попадание второго орудия)
независимы.
Вероятность события А*В (оба орудия дали попадание)
Р(А*В)=Р(А)*Р(В)=0,7*0,8=0,56
Искомая вероятность Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,7+0,8-0,56=0,94

15.

Решаем задачи. Выполняем упражнения
Пример 3: Прибор, состоящий из двух блоков, выходит из строя, если
выходят из строя оба блока. Вероятность безотказной работы за
определенный промежуток времени первого блока составляет 0,9, второго
– 0,8, обоих блоков – 0,75. Найти вероятность безотказной работы прибора
в течение указанного промежутка.
Решение. Обозначим через А событие «первый блок работает
безотказно в течение определенного промежутка времени», через В
событие «второй блок работает безотказно в течение определенного
промежутка времени», через АВ событие «оба блока работают безотказно
в течение определенного промежутка времени». Событие С «прибор
работает безотказно в течение определенного промежутка времени»
является суммой событий А и В: C = A + B . Из условия задачи известны
вероятности P(A) = 0,9 , P(B) = 0,8 и P(AB) = 0,75 . По формуле сложения
вероятностей имеем:
Р( C)= P (A+ B)= P( A)+ P( B) - P( AB)= 0,9+ 0,8 - 0, 75= 0,95.
Ответ: 0,95

16. Задача 2

Из колоды в 36 карт случайно вынимают две карты. С
какой вероятностью они будут одной масти?

17. Задача 3

В мешке есть белые, желтые и черные кубики. При этом
10% от общего числа — белые, 15% от общего числа —
желтые. Из мешка случайно вытаскивается кубик.
а) Какова вероятность, что этот кубик светлый?
б) Какова вероятность, что этот кубик черный?

18. СР в парах по вариантам

СР в па р а х по вариантам
Нечетная пара
Четная пара

19.

20.

21.

22. Итоги урока

23. Итоги урока

24.

Домашнее з а д а н и е № 2 7
Теория:
Учебник Ч2 : §53 стр. 29-31, ответить на вопросы 1-4,
разобрать материал по конспекту
Выполнить: № 82 , 83, 84, 85