Скалярное произведение векторов

1. Геометрия 10 класс

2.

3.

4.

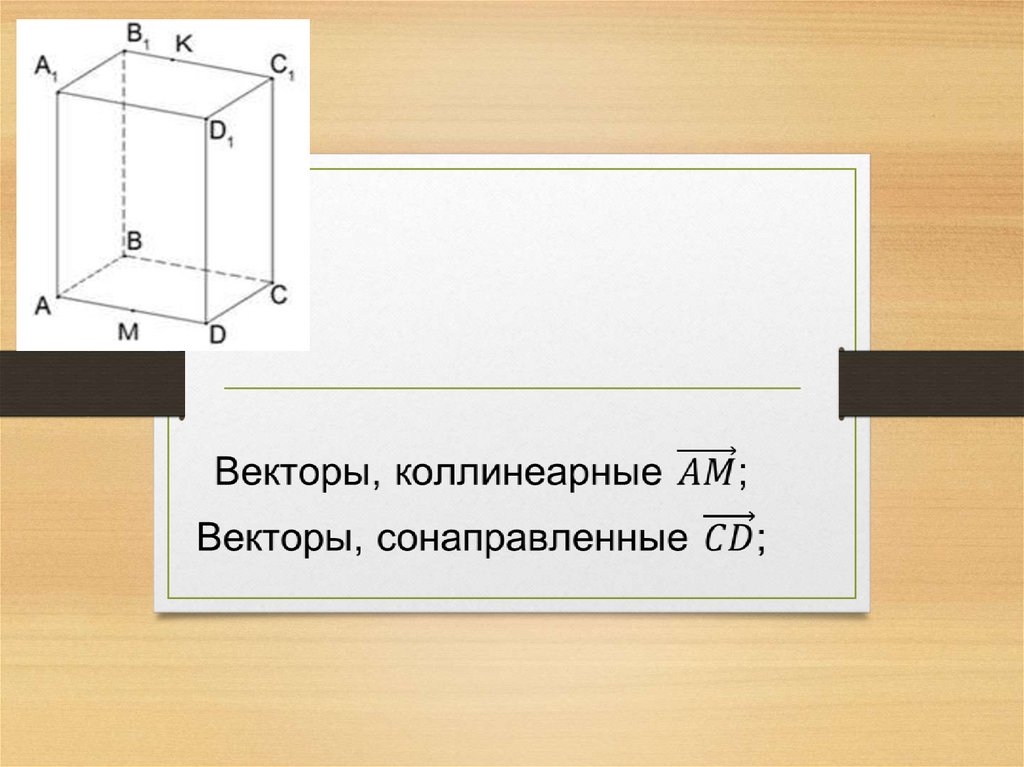
Угол между векторами
b
О
a
Угол между векторами
равен .
a b =
aиb

5.

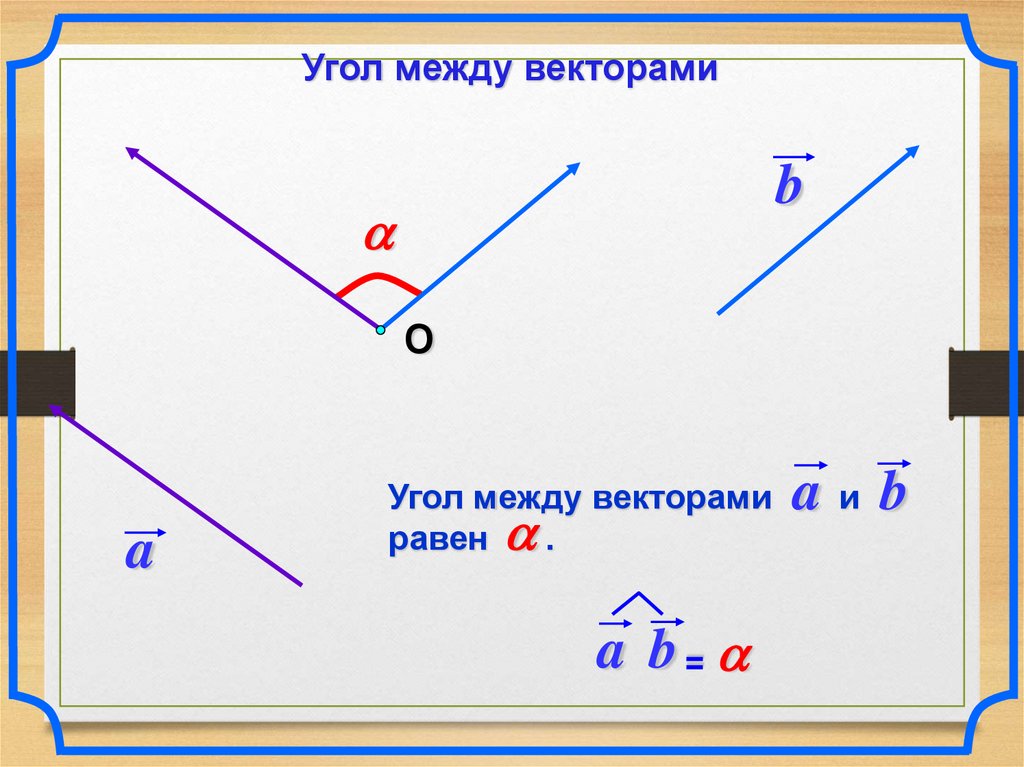
Найдите угол между векторами
a b = 300
a
a c = 1200
d
300
c
b
f
b c = 900
d c = 1800
d f = 00

6.

ТЕМА УРОКА:
Скалярное
произведение векторов

7. Цель урока:

10.4.4 –знать определение и свойства скалярного
произведения векторов

8.

Определение
Скалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число
(скаляр).

9.

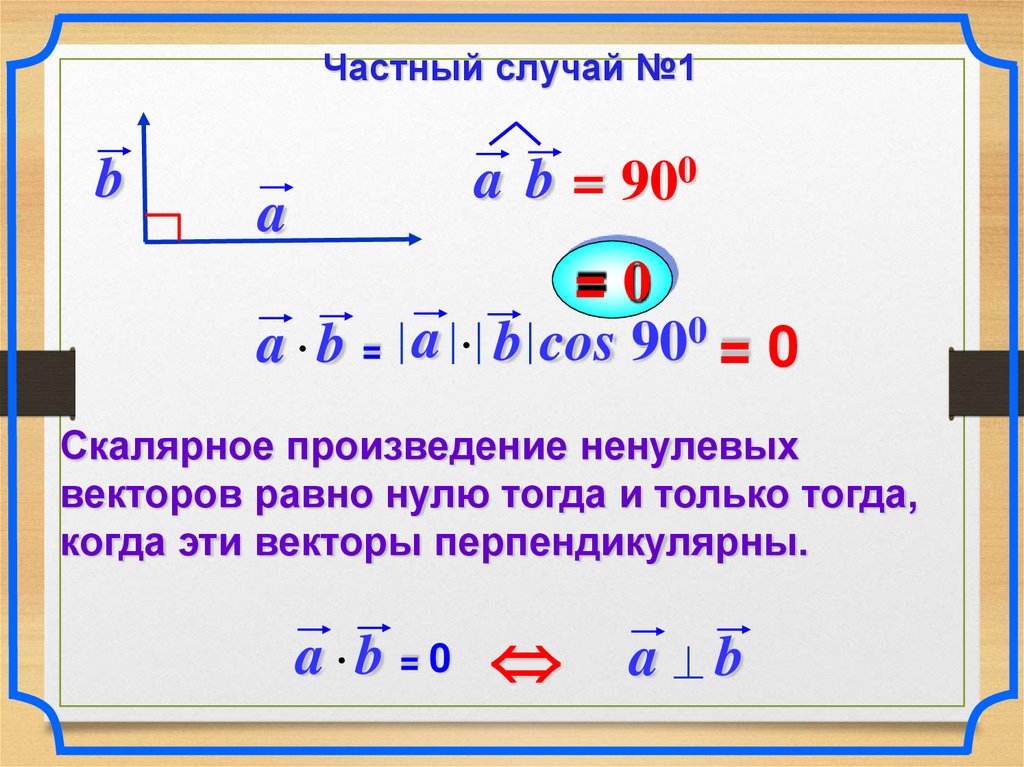
Частный случай №1
b
a
a b = 900
=0
a b = a b cos 900 = 0
Скалярное произведение ненулевых
векторов равно нулю тогда и только тогда,
когда эти векторы перпендикулярны.
a b = 0
a b

10.

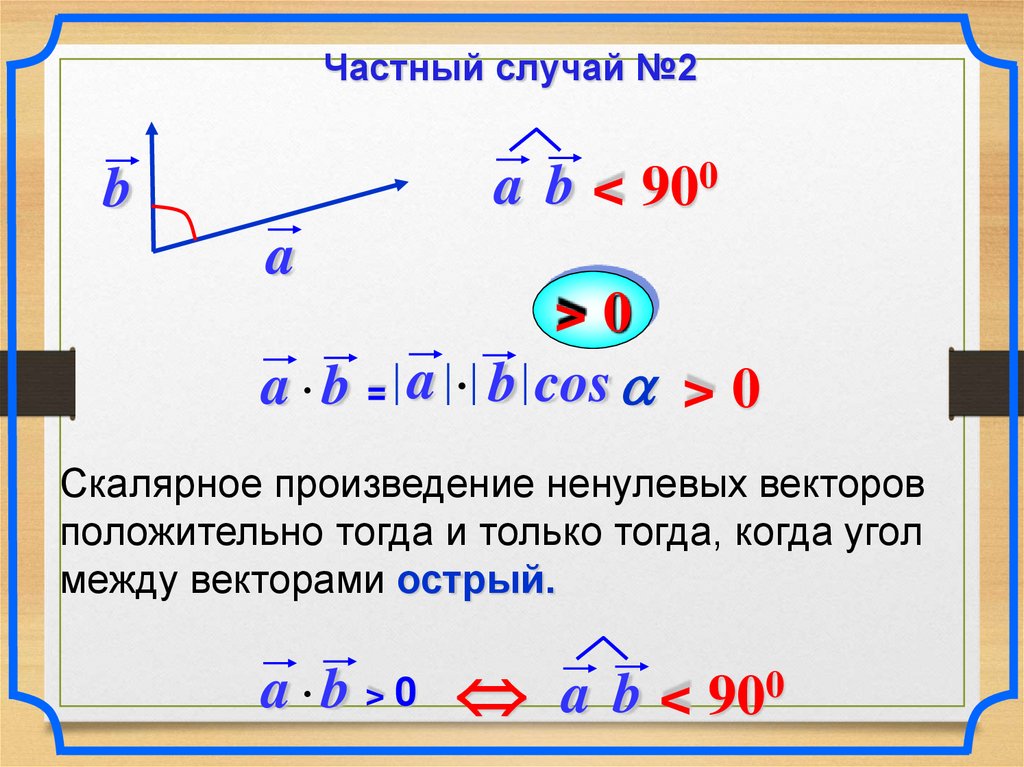
Частный случай №2
a b < 900
b
a
>0
a b = a b cos > 0
Скалярное произведение ненулевых векторов
положительно тогда и только тогда, когда угол
между векторами острый.
a b > 0 a b < 900

11.

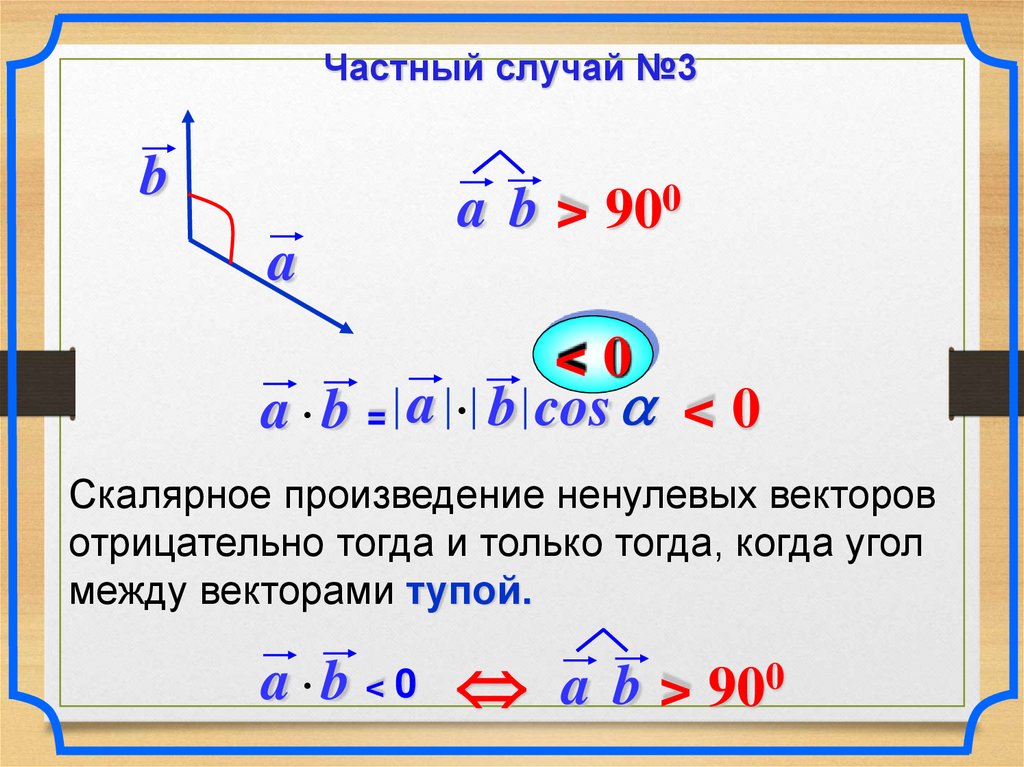
Частный случай №3
b
a b > 900
a
<0
a b = a b cos < 0
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда, когда угол
между векторами тупой.
a b < 0 a b > 900

12.

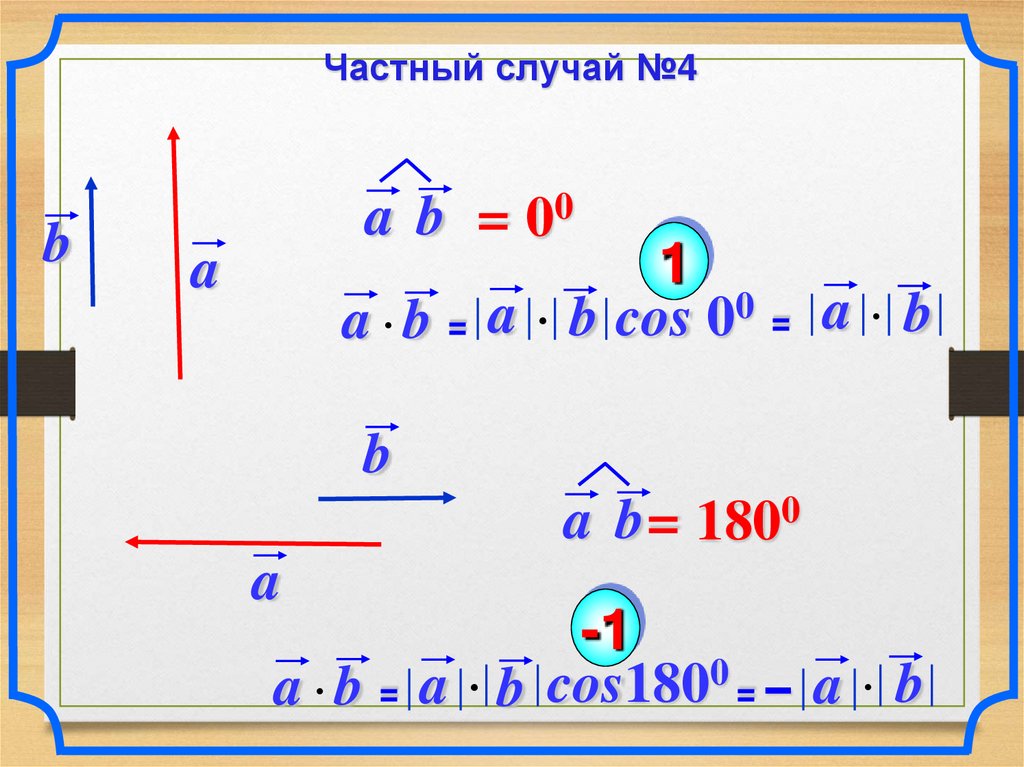
Частный случай №4
b
a b = 00
1
a b = a b cos 00 = a b
a
b
a b = 1800
a
-1
a b = a b cos1800 = – a b

13.

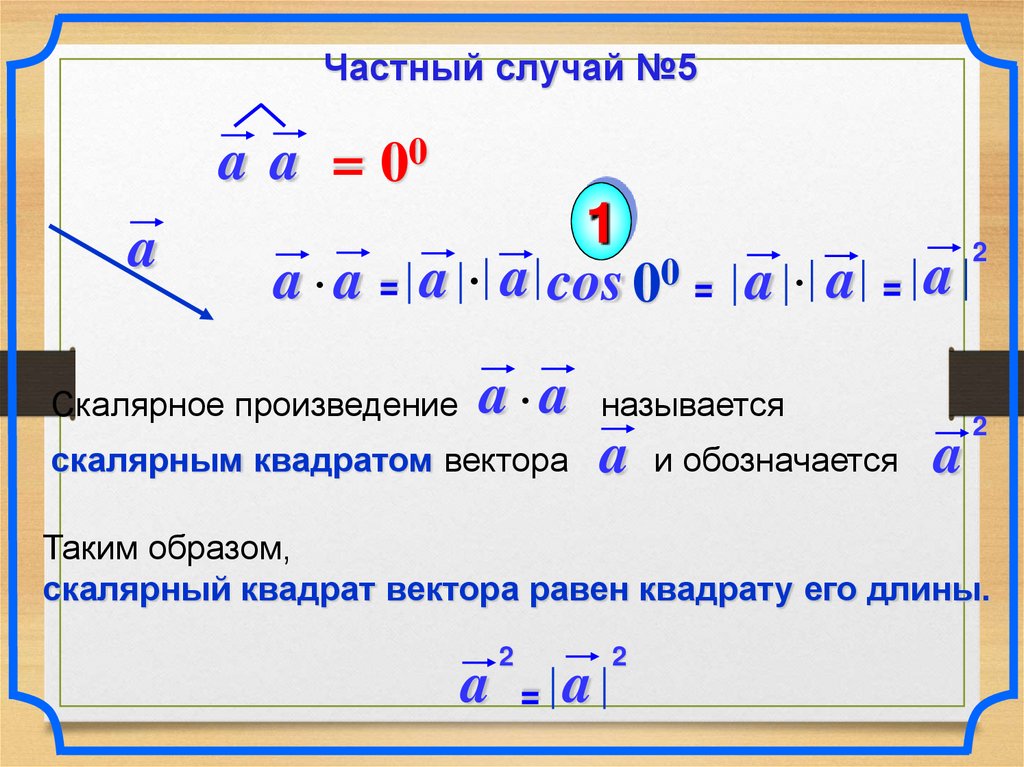
Частный случай №5
a a = 00
a
1
2
a a = a a cos 00 = a a = a
a a называется
2
скалярным квадратом вектора a и обозначается a
Скалярное произведение
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
2
a =a
2

14.

15. Тема урока : Скалярное произведение векторов.

Цель урока:
10.4.16 – знать формулу скалярного
произведения векторов в координатной форме
и применять ее при решении задач

16.

Формула для нахождения
скалярного произведения
через координаты векторов
a = x1 i + y1 j + z 1 k
a b= ?
b = x2 i + y2 j + z 2 k
a b= (x1 i + y1 j + z1 k) (x2 i + y2 j + z2 k) =
= x1x2 + y1y2 + z1z2
a b = x1x2 + y1y2 + z1z2

17.

Пример №1
Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0; 7}
a b= x1x2 + y1y2 + z1z2
a b= -6 (-1) + 9 0 + 5 7 = 41

18.

Проверочная работа
1. Найти скалярное произведение векторов:
a {1; 10; 7}
b {0; 7; 0}

19.

20.

Проверочная работа
3. Найти скалярное произведение векторов:
a {|-2|; 0; |3|}
b {1; |-11|; 1}

21.

Проверочная работа
4. Найти скалярное произведение векторов:
a {sin(900); 2; 3}
b {3; 2; 1}

22.

Проверочная работа
5. Найти скалярное произведение векторов:
a {-1; 2; 8}
b {5; 5; 0}

23.

Проверочная работа
Работа закончена.
Перейдём к проверке.

24.

Проверочная работа
1. Найти скалярное произведение векторов:
a {1; 10; 7}
b {0; 7; 0}
a b= 10 7 = 70

25.

Проверочная работа
2. Найти скалярное произведение векторов:
a {7; 25; 0}
b {11; 0; 54}
a b= 7 11 = 77

26.

Проверочная работа
3. Найти скалярное произведение векторов:
a {|-2|; 0; |3|}
b {1; |-11|; 1}
a b= 2 1 + 3 1 = 5

27.

Проверочная работа
4. Найти скалярное произведение векторов:
a {sin(900); 2; 3}
b {3; 2; 1}
a b= 1 3 + 2 2 + 3 1 = 10

28.

Проверочная работа
5. Найти скалярное произведение векторов:
a {-1; 2; 8}
b {5; 5; 0}
a b= -1 5 + 2 5 = 5

29. Итог урока

Что чувствовали сегодня на уроке?
С какими трудностями ввстретились?
Кому было трудно? Почему? Что ты
сделал, чтобы преодолеть эту трудность?
Что тебе помогло? (Опорные конспекты,
подсказки товарищей…)