Similar presentations:
Свойства и таблица неопределённых интегралов
1. СВОЙСТВА И ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
2. Неопределенный интеграл
ОПР. Совокупность всех первообразныхF ( x ) C для данной функции f ( x )
называется ее неопределенным интегралом
и обозначается
f ( x)dx F ( x) C ,
где
C
– произвольная постоянная.
3.
Знакназывается интегралом, функция
f (x) – подынтегральной функцией,
f ( x)dx – подынтегральным выражением,
x
– переменной интегрирования.
Операция нахождения неопределенного
интеграла для данной функции называется
интегрированием этой функции.
Интегрирование – операция, обратная
операции дифференцирования.
4. Основные свойства неопределенного интеграла
1. Дифференциал от неопределенногоинтеграла
равен
подынтегральному
выражению:
d f ( x )dx f ( x )dx
5.
2.Производная
интеграла
равна
функции:
неопределенного
подынтегральной
f ( x)dx f ( x).
!!!! Таким образом,
правильность интегрирования проверяется
дифференцированием!
6.
3.Неопределенный
интеграл
от
дифференциала некоторой функции равен
сумме этой функции и произвольной
постоянной:
dF
(
x
)
F
(
x
)
C
.
7.
4. Постоянный множительвыносить за знак интеграла:
можно
af
(
x
)
dx
a
f
(
x
)
dx
.
8.
5.Неопределенный
интеграл
от
алгебраической суммы конечного числа
непрерывных
функций
равен
алгебраической сумме интегралов от
слагаемых функций:
f ( x) g( x) dx f ( x)dx g( x)dx.
9.
6. Если f ( x ) dx F ( x ) C , тоf (u) du F (u) C ,
где u ( x )
− произвольная функция,
имеющая непрерывную производную.
Данное
свойство
называется
инвариантностью
неопределенного
интеграла.
10.
Привычислении
неопределенного
интеграла используют формулу:
1
f (ax b)dx a F (ax b) C , a 0.
11. Таблица простейших интегралов
1. 0 du C;3. u du
1
u
1
2. 1 du u C;
C , 1;
1
1
4. 2 du C ;
u
u
1
6. du ln u C ;
u
1
5.
du 2 u C ;
u
u
a
u
7. a du
C;
ln a
9. sin udu cos u C;
10. cos udu sin u C;
1
11.
du tgu C ;
2
cos u
1
12. 2 du ctgu C ;
sin u
8. e udu e u C;
12.
11
u
13. 2
du arctg C ;
2
u a
a
a
14.
1
u
du arcsin C ;
2
2
a
a u
du
1
u a
15. 2
ln
C;
2
u a
2a u a
16.
du
u2 a 2
ln u u a C .
2
2











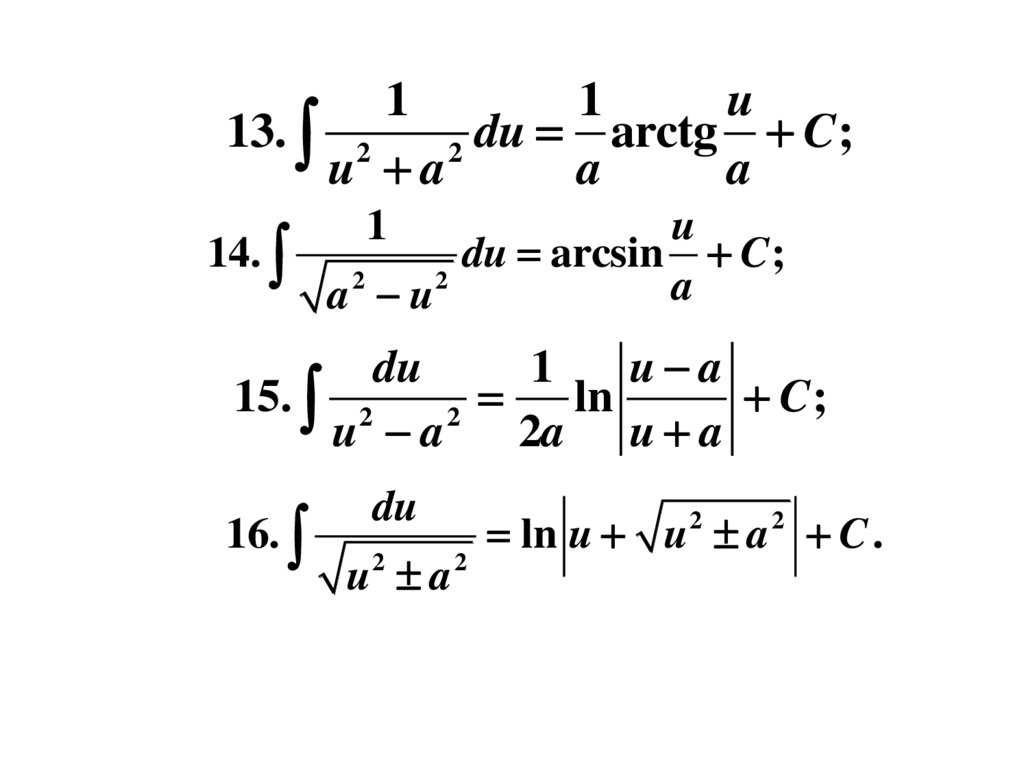
 mathematics
mathematics








