Понятие числовой последовательности

1.

Понятие
числовой
последовательности

2.

3.

Последовательности составляют такие элементы
природы, которые можно как то пронумеровать.
Дни
недели
Дома
на улице
Классы
в школе
Названия
месяцев
Номер
счёта
в банке

4.

В сберегательном банке по номеру лицевого счета
вкладчика можно легко найти этот счет и посмотреть,
какой вклад на нем лежит.
Пусть на счете №1 лежит вклад а1 рублей,
на счете №2 - а2 рублей и т.д.
Получается числовая последовательность:
а1, а2, а3, …, аn
где N – число всех счетов.
Здесь каждому натуральному числу n от 1 до N
поставлено в соответствие число аn

5.

Функцию
называют функцией
натурального аргумента или числовой
последовательностью и обозначают
Последовательности могут быть конечными и
бесконечными, возрастающими и убывающими.

6.

Последовательности могут быть конечными и
бесконечными, возрастающими и убывающими.
1. Конечные:
Пример: последовательность положительных
двузначных чисел:
10,11,12,….98,99.
2. Бесконечные:
Пример: положительные четные числа:
2,4,6,8,10,…

7.

Последовательность с помощью формулы n-ного члена.
Это позволяет вычислить член с любым заданным номером.
1) аn=2n+3
a1=2·1+3=5 a2=2·2+3=7 a3=2·3+3
2) an=100-10n2.
Найдите первые три члена.
3) an=n2-2n-6.
Является ли членом
последовательности (-3)?
-стационарная последовательность

8.

Описывает способ получения членов последовательности.
1) 3; 7; 13; 19; 29; … - последовательность
простых чисел (через одно)
2) 1, 3, 5, 7, 9. – последовательность
нечетных однозначных чисел.

9.

Формулу, выражающую любой член последовательности,
начиная с некоторого, через предыдущие (один или несколько),
называют рекуррентной (от латинского слова recurro–
возвращаться).
Дана последовательность:
а1=1, а2=3, аn+2=2аn+аn+1
а3=2а1+а2=2.1+3=5
а4=2а2+а3=2.3+5=11
а5=2а3+а4=2.5+11=21 …

10.

Среди рекурретно заданных последовательностей особо
выделяют два наиболее простых и в то же время важных
случая.
Первый случай-арифметическая прогрессия
Указан первый член последовательности
и задано рекуррентное соотношение
Второй случай –геометрическая прогрессия
Указан первый член последовательности
и задано рекуррентное соотношение

11.

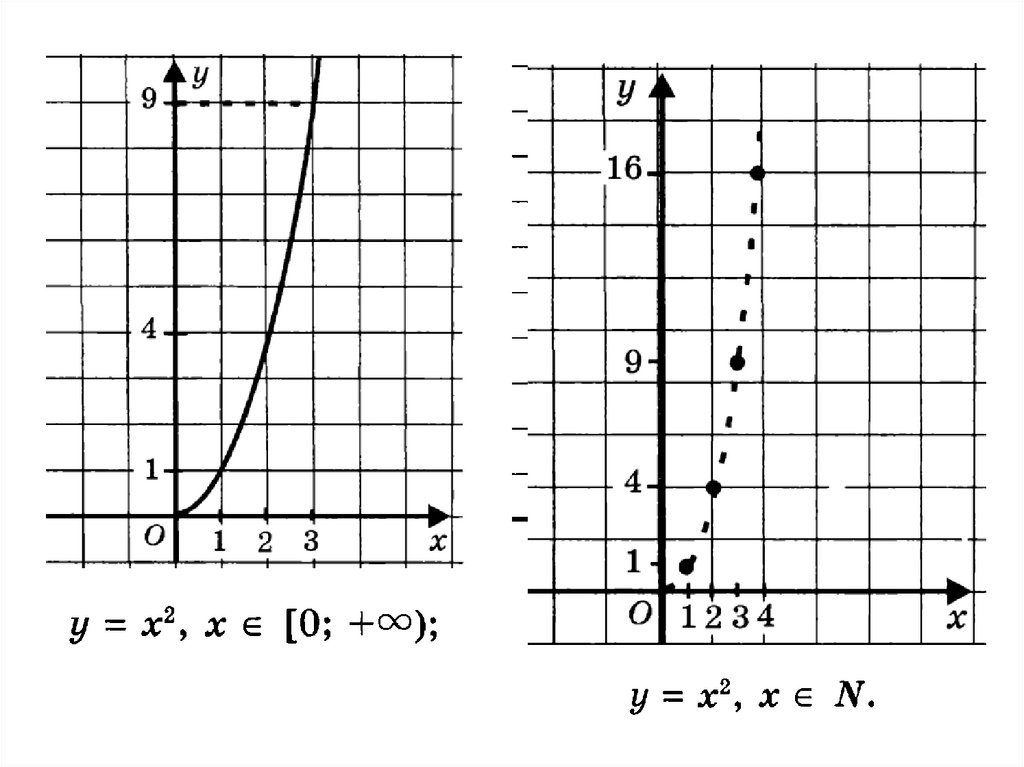
Числовая последовательность - частный случай числовой
функции.
Последовательность
называют возрастающей, если
каждый ее член (кроме первого) больше предыдущего:
Последовательность
называют убывающей, если
каждый ее член (кроме первого) меньше предыдущего: