Similar presentations:
Дифференциальное исчисление функций одной переменной. Лекция 5
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы Екатерины II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
ЛЕКЦИЯ 5
Исследование функций с помощью
производных
16.03.2025
1|20
2.
Содержание лекции• Монотонность функции;
• Необходимое и достаточное условия экстремума;
• Выпуклость и вогнутость графика функции,
• Точки перегиба графика функции;
• Асимптоты графика функции.
2|20
3.
Возрастание и убывание функцииf(x) диф-ма на (a;b), f(x) =const x ( a; b) : f ( x) 0
Постоянство
f(x):
Критерий
монотонности
дифференцируемой
функции
Дифференцируемая функция f(x)
возрастает (убывает) на (a;b)
Необходимость
f ( x) 0, x (a; b) f ( x) 0
Пусть х0 (a,b) – произвольная точка и функция f(x) возрастает
x x f ( x ) f ( x )
x ( a; b )
x x f ( x ) f ( x )
при предельном переходе
если х (a;b) и х х0, f ( x ) f ( x )
сохраняется знак
то выполняется
x x
нестрогого неравенства
неравенство
x x
Достаточность
f ( x0 )
f ( x ) , x ( a;b )
f ( x ) , x ( a; b ) Пусть х1, х2 – произвольные точки (a;b), чтобы x1<x2
На [x1; x2] применим теорему Лагранжа: f ( x ) f ( x ) f ( c )( x x ) 0
с (x1; x2) 0
0
x , x ( a;b ) : x x f ( x ) f ( x )
3|20
4.
Достаточное условие строгоймонотонности
x (a; b) : f ( x) 0 f(x) строго возрастает на (a;b)
x (a; b) : f ( x) 0 f(x) строго убывает на (a;b)
Доказательство:
x ( a; b ) : f ( x )
Пусть х1, х2 – произвольные точки (a;b), чтобы x1<x2
По теореме Лагранжа для [x1; x2] :
с (x1; x2)
f ( x2 ) f ( x1 ) f (c)( x2 x1 ) f ( x2 ) f ( x1 )
0
Замечание: Условияf ( x )
функция f(x)=x3 строго возрастает
не являются необходимыми
для строгой монотонности
f ( x) 3x 2
4|20
f (0) 0
5.
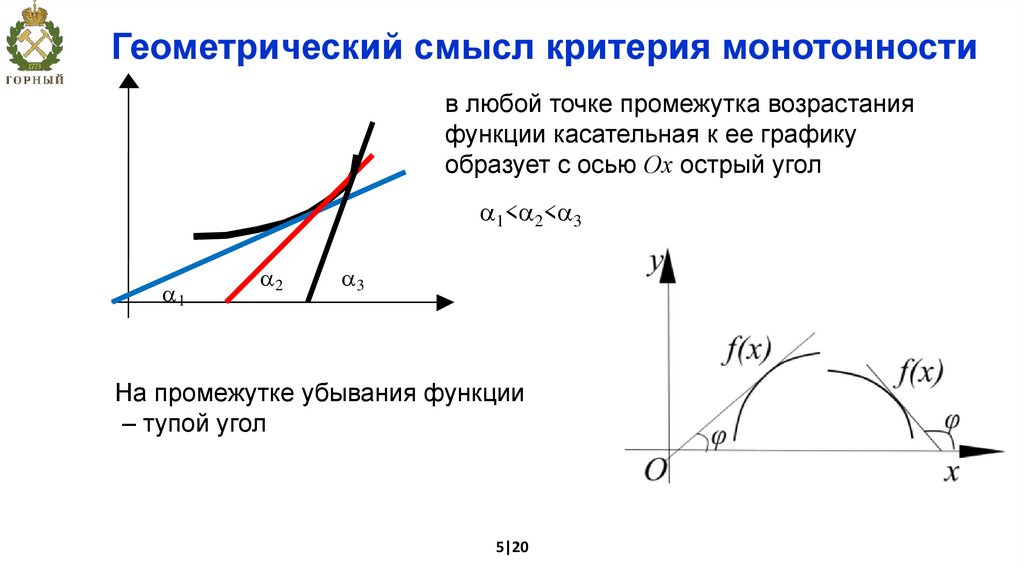
Геометрический смысл критерия монотонностив любой точке промежутка возрастания
функции касательная к ее графику
образует с осью Ох острый угол
1< 2< 3
1
2
3
На промежутке убывания функции
– тупой угол
5|20
6.
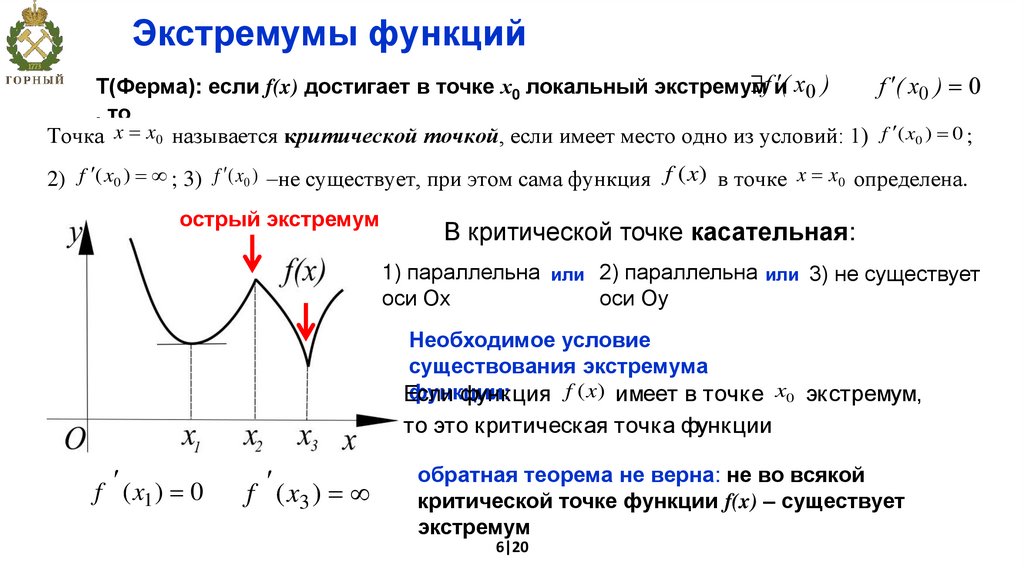
Экстремумы функцийf и ( x )
f ( x )
Т(Ферма): если f(x) достигает в точке х0 локальный экстремум
, то
Точка x x0 называется критической точкой, если имеет место одно из условий: 1) f ( x0 ) 0 ;
2) f ( x0 ) ; 3) f ( x0 ) –не существует, при этом сама функция f (x) в точке x x0 определена.
острый экстремум
В критической точке касательная:
1) параллельна или 2) параллельна или 3) не существует
оси Ох
оси Оу
Необходимое условие
существования экстремума
функции:
Если
функция f (x) имеет в точке x0 экстремум,
то это критическая точка функции
f (x ) 0
1
f (x )
3
обратная теорема не верна: не во всякой
критической точке функции f(x) – существует
экстремум
6|20
7.
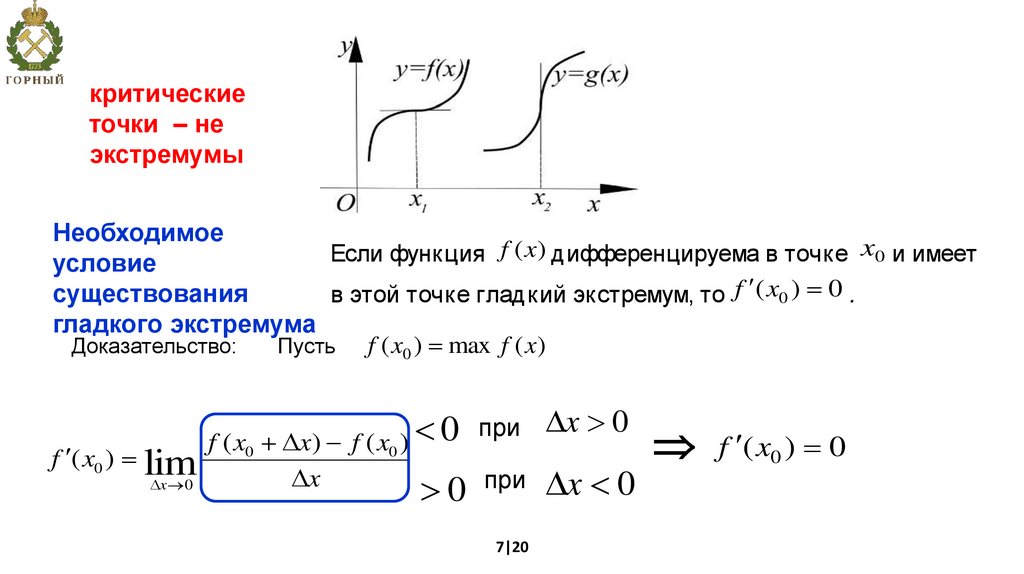
критическиеточки – не
экстремумы
Необходимое
f (x) дифференцируема в точке x0 и имеет
Если
функция
условие
существования
в этой точке гладкий экстремум, то f ( x0 ) 0 .
гладкого экстремума
Доказательство:
Пусть f ( x0 ) max f ( x)
f ( x0 ) lim
x 0
при x 0
0
f ( x0 x) f ( x0 )
f ( x ) 0
x
0 при x 0
7|20
0
8.
Достаточное условие существования экстремумачерез 1-ю производную:
Пусть функция f(x) дифференцируема в некоторой окрестности точки
х0 (кроме, быть может, х0) и непрерывна в точке х0.
Тогда если f (x ) при переходе через точку х0 :
1) меняет знак с «–» на «+», то х0 – точка минимума;
2) меняет знак с «+» на «–», то х0 – точка максимума;
3) не меняет знак, то в х0 экстремума нет.
Доказательство:
f ( x) 0
x0
f (x ) при переходе через точку х0 меняет знак с «–» на «+» :
f ( x) 0
x0
x0
Теорема Лагранжа
[x;x0] x c x0
0
0
f ( x ) f ( x ) f ( c )( x x )
[x0;x]
x0 c x
8|20
0
0
f ( x) f ( x0 )
х0 – точка
минимума
9.
Достаточное условие существования экстремумачерез 2-ю производную
Пусть в точке x0 и в некоторой её окрестности функция f (x)
дважды непрерывно дифференцируема и f ( x0 ) 0 . Тогда
Если f ( x0 ) 0 , то х0 – точка минимума
Если f ( x0 ) 0 , то х0 – точка максимума
Доказательство:
формула Тейлора в окрестности точки х0
f x0
f c
2
f ( x) f x0
x x0
x x0 , c x0 , x
1!
2!
0
0
f (c)
2
f ( x) f ( x0 )
( x x0 ) .
2!
f ( x) f ( x0 )
9|20
х0 – точка
максимума
10.
Достаточное условие существования экстремумачерез n-ю производную
Пусть существует f ( n) ( x0 ),
( n 1)
( n)
f
(
x
)
f
(
x
)
...
f
(
x
)
0
,
f
( x0 ) 0
n 2 и
0
0
0
Тогда:
1) если n – четное, то при
f ( n )( x ) – х
0
точка максимума;
f ( n )( x ) – х0 точка минимума;
2) если n – нечетное, то х0 не является точкой экстремума.
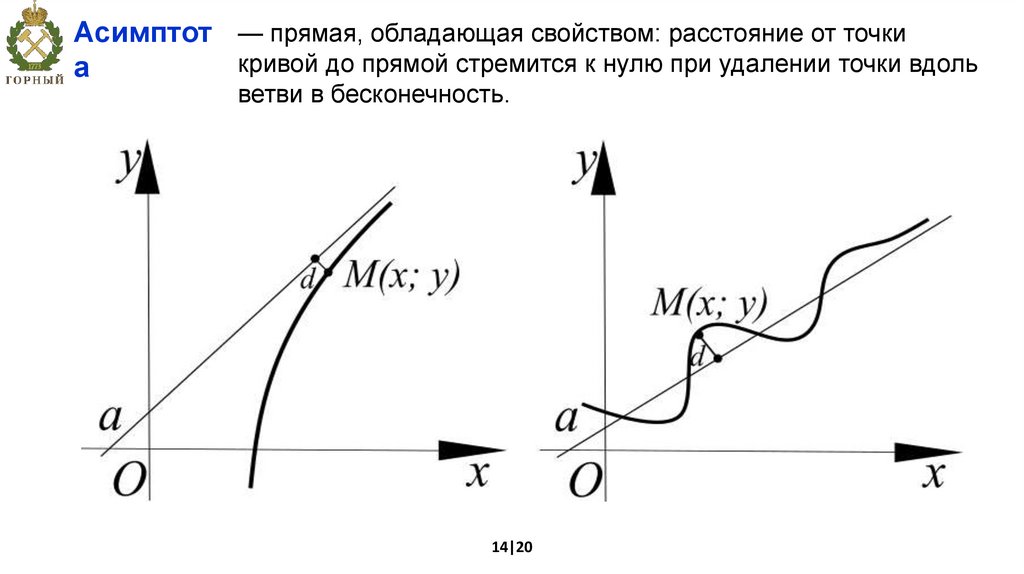
Наименьшее и наибольшее значения функции на отрезке
f(x) – непрерывна
a, b
Если достигается во
внутренней точке
существуют
Поиск min[а,













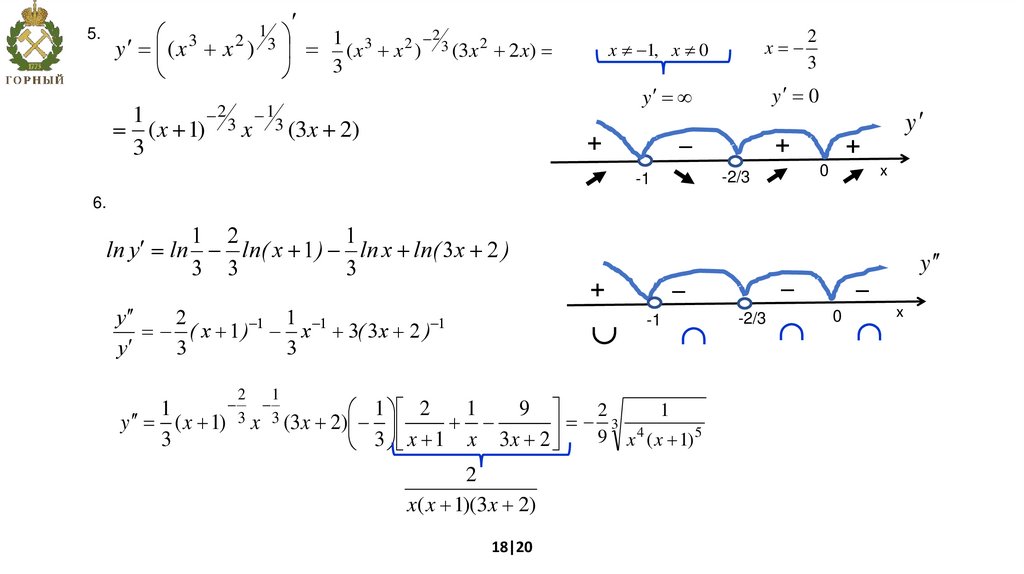
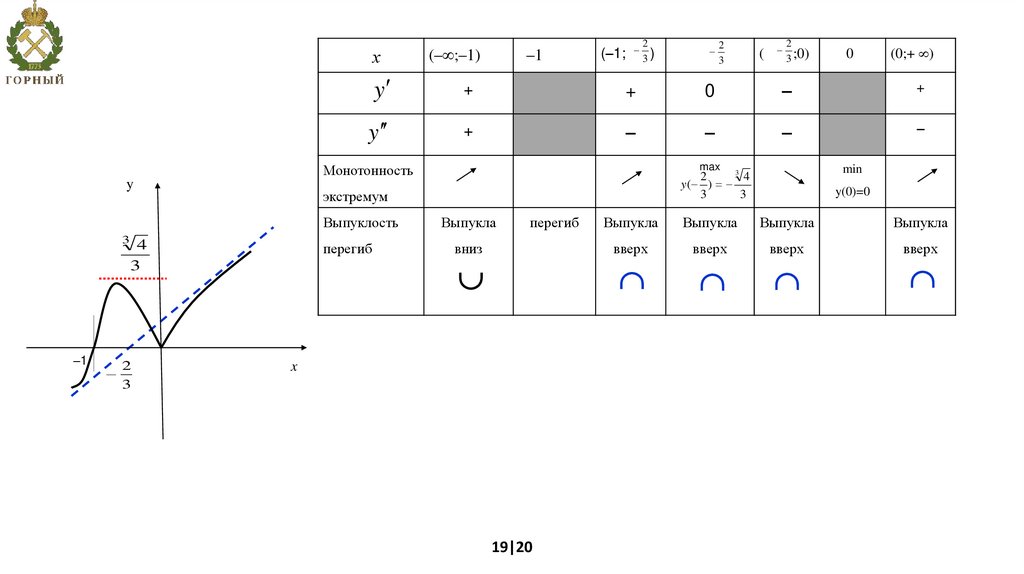

 mathematics
mathematics








