Сума перших n членів арифметичної прогресії

1. Сума перших n членів арифметичної прогресії.

Тема уроку:

2. Мета уроку:

Домогтися засвоєння формули для
обчислення суми перших n членів
арифметичної прогресії; сформувати
вміння застосовувати цю формулу до
розв’язування задач;
Формувати вміння висловлювати
власну думку,слухати і чути інших;
Сприяти самовихованню об’єктивності,
чесності, відповідальності.

3. !1. Дайте означення арифметичної прогресії.

Відповідь: Арифметичною
прогресією називається числова
послідовність, кожний член якої,
начинаючи з другого, дорівнює
попередньому, до якого додається
одне й те ж число.
аn 1 an d

4. ! 2. Що називають різницею арифметичної прогресії? Як позначають?

Відповідь: це число, яке показує на
скільки кожний наступний член
більший або менший попереднього.
Позначають буквою d.

5. ! 3. Назвати формулу n-ого члена арифметичної прогресії.

an a1 (n 1) d

6. !4. Які властивості арифметичної прогресії?

Відповідь: Кожний член
арифметичної прогресії, починаючи з
другого дорівнює середньому
арифметичному двох сусідніх з ним
членів.
an 1 an 1
аn
2

7. !5. Який спосіб задання арифметичної прогресії ви знаєте?

a1 a1 , аn 1 аn d

8. ! 6. Які бувають арифметичні прогресії?

Відповідь:
Якщо в арифметичній прогресії
різниця
d > 0, то прогресія є
зростаючою.
Якщо в арифметичній прогресії різниця
d <0, то прогресія є спадною.
Якщо в арифметичній прогресії d = 0,
то прогресія є сталою.

9.

Актуальна задача
На шоу талантів “Голос країни” після
виступу всіх учасників глядачі протягом
30 хв могли взяти участь в смс голосуванні за улюбленого учасника.
Протягом першої хвилини від початку
свою думку висловили 4800 глядачів.
Протягом кожної наступної хвилини
голосувало на 160 глядачів менше, ніж
попередньої хвилини.

10.

1. Скільки глядачів проголосували протягом
другої хвилини від початку голосування?
2. Скільки глядачів проголосували протягом
третьої хвилини від початку голосування?
3. Складіть формулу, за якою обчислюється
кількість глядачів, які проголосували протягом
n-ї хвилини від початку голосування (1≤n≤30).
4. Скільки глядачів проголосували протягом 30
хвилин.

11.

Нехай треба знайти суму членів арифметичної прогресії:
a1 , a2, a3, …, an-2 , an-1 , an .
Позначають таку суму зазвичай Sn.
Запишемо цю суму двома способами: у прямому і зворотному порядку
розміщення доданків.
Маємо:
Sn = a1 + a2+ a3+ …+ an-2 + an-1 + an .
Sn = an + an-1 + an-2+... + a3 + a2 + a1,
Додамо почленно ці дві рівності.
Маємо:
2 Sn = (а1 + аn) + (a2 + аn-1) + (a3 + an-2)+ ... +(an-2 + a3)+ (аn-1 + a2 )+(аn + а1).
Кожна із сум у дужках дорівнює а1 + аn
Кількість таких сум дорівнює n.
Отже, 2Sn = (а1 + аn)n.
Звідси:

12.

Враховуючи те, що аn = а1 +d(n - 1), формулу
суми членів арифметичної прогресії можна
записати і в такому вигляді:
За встановленою формулою суму ста перших
натуральних чисел можна обчислити так:

13. Формула суми n перших членів арифметичної прогресії.

Висновок
Формула суми
n перших членів арифметичної
прогресії.
a1 a n
Sn
n
2

14. Робота в групах

Завдання І групі:
1.Чому дорівнює сума семи
перших членів арифметичної
прогресії (аn), якщо
а1=9 і а7=15?
2. Знайдіть суму перших 27
членів арифметичної
прогресії, у якої а1=5 і d=3.
3. Знайдіть суму перших ста
непарних чисел.

15. Робота в групах

Завдання ІІ групі:
1.Чому дорівнює сума дев'яти перших
членів арифметичної прогресії (аn), якщо
а1=4 і а9=18?
2. Знайдіть суму перших 12 членів
арифметичної прогресії, у якої а1=-6 і d=4.
3. Знайдіть суму усіх парних чисел, що
містяться від 1 до 100.

16. Робота в групах

Завдання ІІІ групі:
1.Чому дорівнює сума шести
перших членів арифметичної
прогресії (аn), якщо
а1=20 і а6=15?
2. Знайдіть суму перших 14 членів
арифметичної прогресії, у якої
а1=7 і d=-3.
3. Знайдіть суму усіх натуральних
чисел, кратних 4, що не
перевищують 100.

17.

Карл Гаус
( 1777 – 1855 )
«Математика – цариця всіх наук,
арифметика – цариця математики»
Німецький математик, астроном, геодезист,
фізик, вважається «королем математики».
Народився 30 квітня 1777 року в герцогстві
Брауншвейг у сім’ї садівника. Видатні математичні
здібності проявив вже у ранньому дитинстві.

18.

Знайшов моментально суму
всіх натуральних чисел від 1 до
100, будучи ще учнем
початкової школи.

19.

Як рахував Гаусс?
Розповідають, що незвичайні здібності
видатного німецького математика Карла
Фрідріха Гаусса (1777-1855) почали
виявлятися вже в ранньому віці.
Якось він здивував учителя, миттєво
обчисливши суму перших ста натуральних
чисел.
Він, очевидно, помітив, що в
послідовності
1; 2; 3; 4; ...; 97; 98; 99; 100
сума першого і останнього числа дорівнює
101 (1 + 100 = 101),
другого і передостаннього — теж
101 (2 + 99 = 101),
третього від початку і третього від кінця —
теж
101 (3 + 98 = 101) і т.д.
Всього таких сум можна утворити 50
(остання — 50 + 51). Отже, сума перших ста
натуральних чисел дорівнює
101 • 50 = 5050.

20. Робота з підручником

№ 17.5, 17.13, 17.17(задача з папірусу
Рінда)
.

21.

Задача з папірусу Рінда
100 мір зерна поділили між 5
людьми так, що другий отримав
на стільки ж більше від першого,
на скільки третій отримав більше
другого,
четвертий – більше третього,
а п’ятий – більше четвертого.
Крім того, двоє перших отримали
в 7 разів менше трьох останнніх.
Скільки мір зерна потрібно дати
кожному?

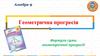
22. Магічний квадрат

9
19
5
7
11
15
17
3
13
Перевіримо, що з кожних дев’яти послідовних членів
будь-якої арифметичної прогресії натуральних чисел
можна скласти магічний квадрат.

23.

24.

Джентльмен отримав спадщину. Перший
місяць він витратив 1000 $, а кожен
наступний місяць він витрачав на 500 $
більше, ніж в попередній. Скільки $ він
витратив за другий місяць? За третій?
Який розмір спадщини, якщо грошей
вистачило на рік такий безбідного життя?

25.

Застосувавши формулу
, отримуємо:
:

26.

10 днів
При зберіганні колод
стройового лісу їх
укладають так, як показано
на малюнку.
78 колод
Курс повітряних ванн
починають з 15 хв. в
перший день і
збільшують час цієї
процедури в кожен
наступний день на 10
хвилин. Скільки днів
слід приймати ванни в
зазначеному режимі,
щоб досягти їх
максимальної
тривалості 1год 45
хвилин?
Скільки колод
знаходиться в одній
кладці, якщо в її основу
покласти 12 колод?

27.

1. В арифметичній прогресії
2,4; 2,6;… різниця дорівнює 2.
2. Четвертий член арифметичної прогресії
0,3; 0,7; 1,1,… дорівнює 1,5
3. 11-ий член арифметичної прогресії, для
якої a1 4,2; d 0,4 дорівнює 0,2

28. На дошці записано всі натуральні числа від 1 до 50,крім чисел, кратних 5. Виберіть із них такі п’ять, які б утворили

арифметичну прогресію.
1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19,21
,22,23,24,26,27,28,29,31,32,33,34,36,37,3
8,39,41, 42,43,44,46,47,48,49.
1,11,21,31,41);
(2,12,22,32,42);
(3,13,23,33,43); (4,14,24,34,44);
(6,16,26,36,46); (7,17,27,37,47);
(8,18,28,38,48); (9,19,29,39,49).

29.

Домашнє завдання:
Вивчити §17;
№ 17.2, 17.4, 17.8, 17.10– обов’язково,
№ 17.22*- додатково.

30. Дякую за увагу!