Механические колебания

1.

2.

Движение, при котором состояния
движущегося тела с течением времени
повторяются, причем тело проходит через
положение своего устойчивого равновесия
поочередно в противоположных направлениях,
называют
механическим колебательным движением.

3.

Виды механического
колебательного движения
Колебания, возникающие в системе под действием
внутренних сил после того, как она была выведена из
положения устойчивого равновесия, и происходящие за счет
расходования сообщенной системе энергии, которая в
дальнейшем не пополняется, называются свободными.
Колебания, совершаемые телами под действием внешних
периодически изменяющихся сил, называются
вынужденными.
Колебания, в которых смещение (координата
колеблющейся точки) изменяется по периодическому закону
синуса или косинуса, называются гармоническими
колебаниями.

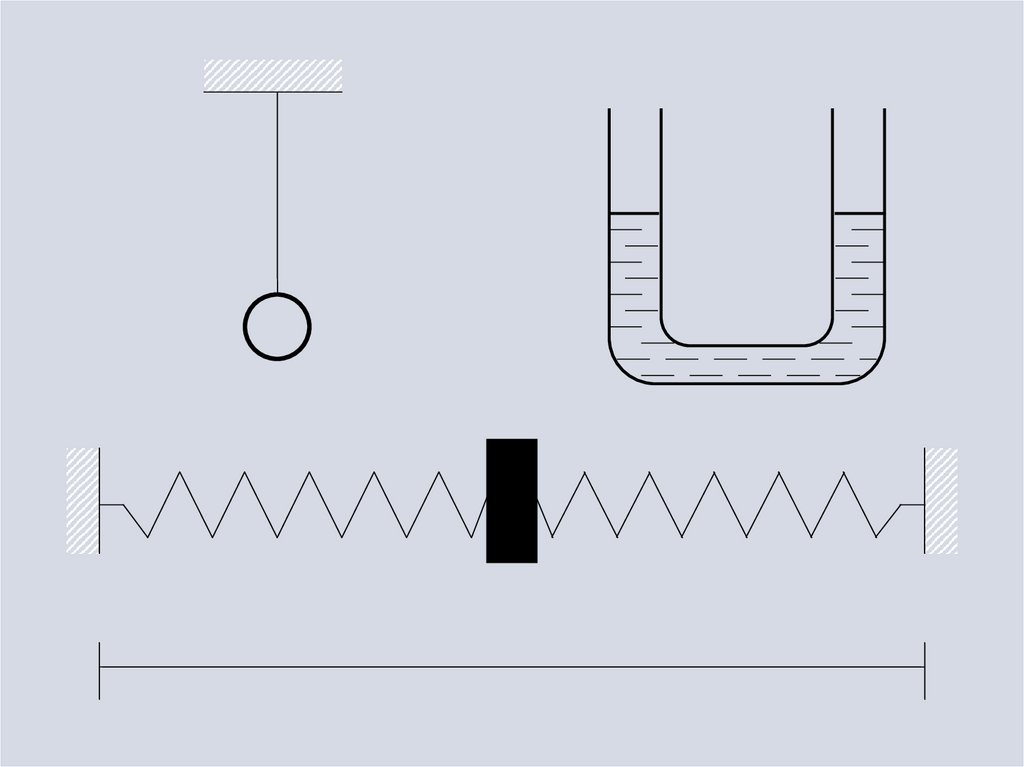
4.

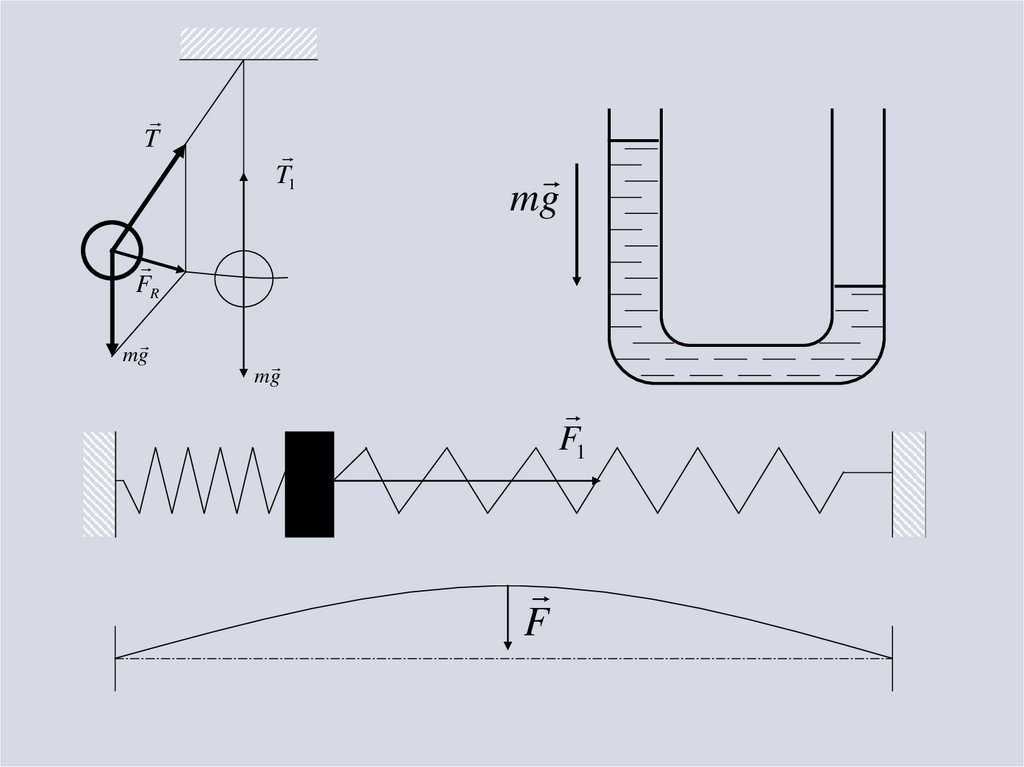
5.

T
T1
mg
FR
mg
mg
F1
F

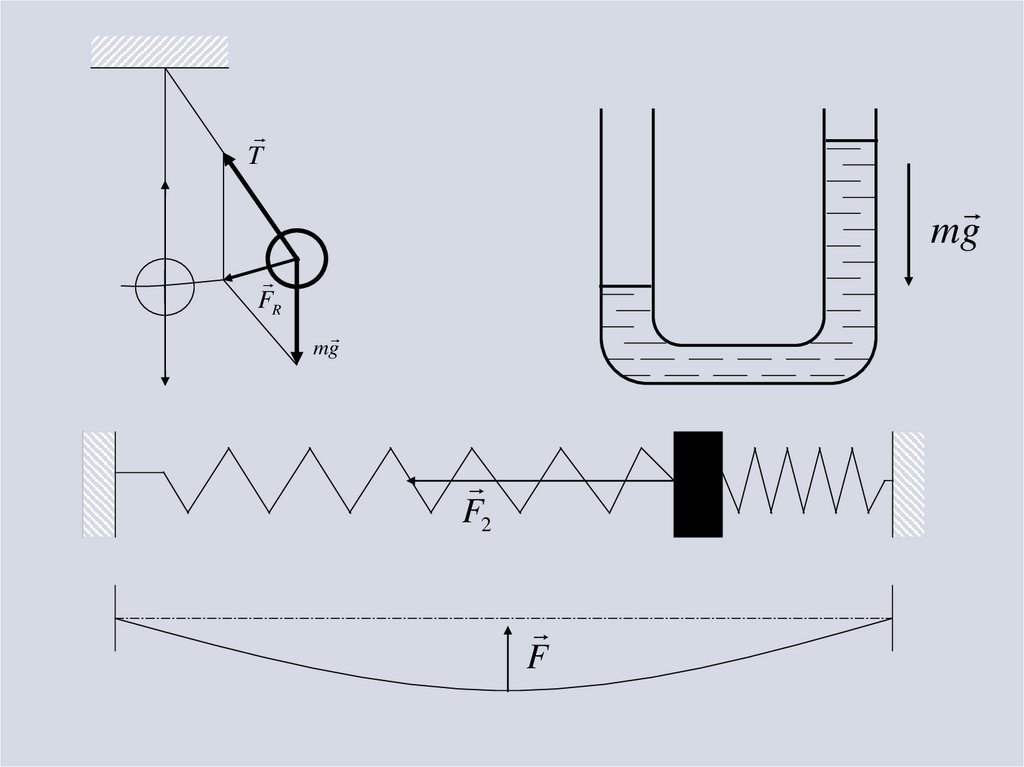
6.

7.

T
mg
FR
mg
F2
F

8.

Параметры колебательного
движения
x A sin( t 0 )
или
x A cos( t 0 )
А – амплитуда колебаний
Т – период колебаний – время одного полного колебания,
измеряется в секундах.

9.

Частота колебаний – величина, равная числу
колебаний в единицу времени.
n
v
t
За единицу частоты, называемую герцем, принята
частота такого колебательного движения, при котором
за каждую секунду совершается одно полное колебание:
1
1Гц
1с 1
1с

10.

2
Циклическая частота 2
- величина, равная
T
числу колебаний в 2π секунд. Она выражается в
1
секундах в минус первой степени: с
Фаза колебания t 0 - физическая величина,
которая полностью определяет смещение
колеблющейся точки в тот или иной момент времени , то
есть ее состояние, 0 - начальная фаза в момент времени
t=0.

11.

Скорость и ускорение при
гармонических колебаниях
Если
x A cos( t 0 ) , то
x x A sin( t 0 )
ax x A cos( t 0 ) x
2
2

12.

x
x A cos t
A
0
T
4
T
2
3
T
4
T
t
T
t
T
t
A
x
A
0
A
x A sin t
T
4
T
2
ax
ax 2 A cos t
2A
0
A
2
3
T
4
T
4
T
2
3
T
4

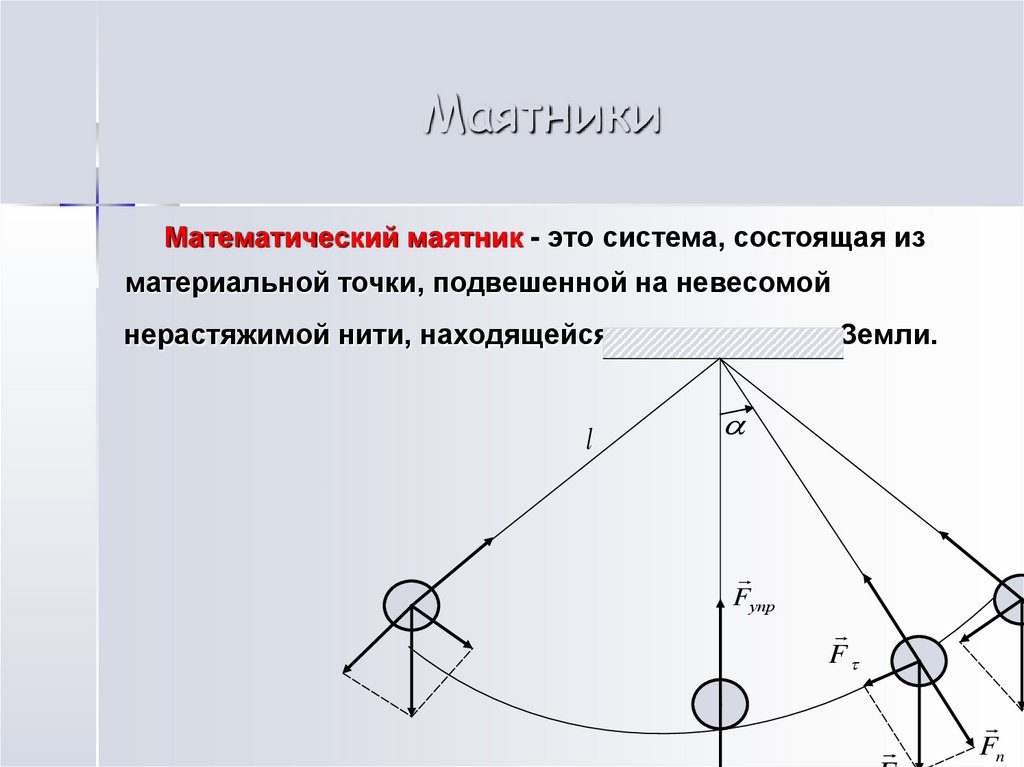
13.

Маятники
Математический маятник - это система, состоящая из
материальной точки, подвешенной на невесомой
нерастяжимой нити, находящейся в поле тяжести Земли.
l
Fупр
F
Fn

14.

Тангенциальная составляющая F силы тяжести создает
тангенциальное ускорение, характеризующее изменение
скорости по модулю. Она всегда направлена к положению
равновесия. При движении маятника эта составляющая силы
тяжести в момент, когда маятник проходит через положение
равновесия, становится равной нулю. Вследствие своей
инертности маятник движется дальше, поднимаясь вверх. При
этом составляющая F силы тяжести шарика уже будет
направлена против скорости. Поэтому модуль скорости
маятника уменьшается. В момент остановки маятника, в
верхней точке модуль F максимален; эта составляющая
направлена в сторону положения равновесия. Далее скорость
маятника увеличивается по модулю, и он снова движется к
положению равновесия. Пройдя положение равновесия, он
возвращается в исходное положение.

15.

F FT sin mg sin
Знак минус в формуле ставят потому, что сила F
направлена к положению равновесия, а смещение
отсчитывают от положения равновесия.
Согласно второму закону Ньютона F ma .
Следовательно, ma mg sin или a g sin
При малых углах sin
2
x
, поэтому
g
a x
Известно, что T
, следовательно T 2
g
.

16.

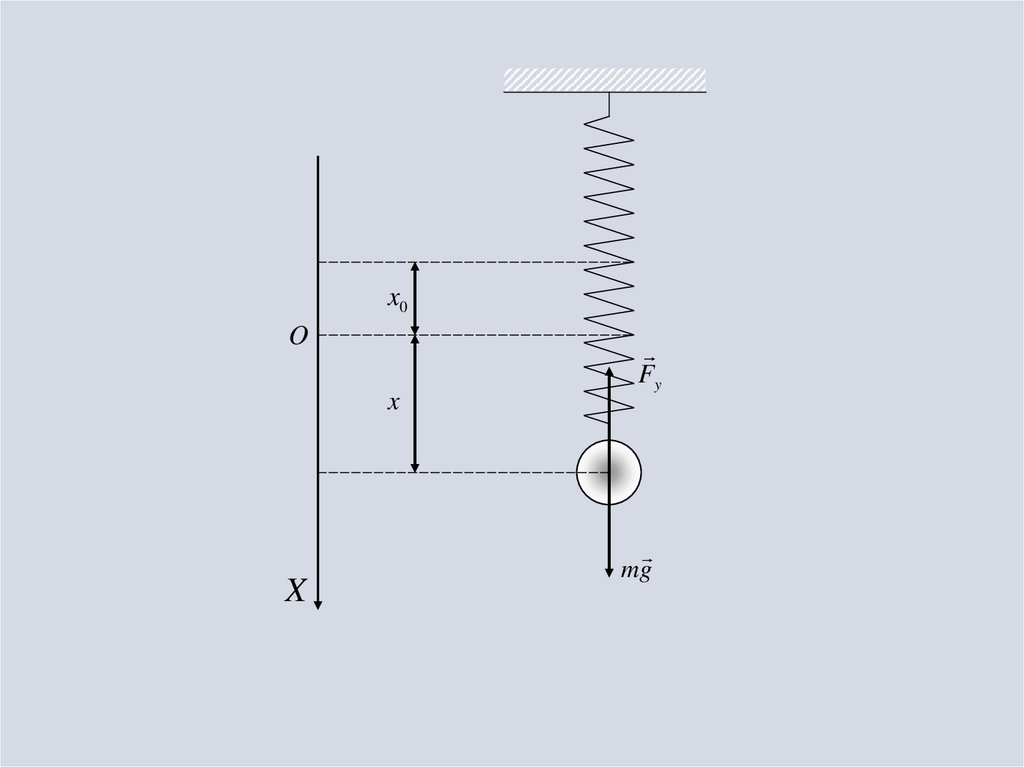
Пружинный маятник
Пружинный маятник – колебательная система,
представляющая собой совокупность некоторого
тела массы m и прикрепленной к нему пружины,
массой которой можно пренебречь по сравнению с
массой тела.
По второму закону Ньютона ma Fупр , так как
силы Fm и N
уравновешивают друг друга.
ma x kx или
k
ax x
m

17.

x0
O
x
X
Fy
mg

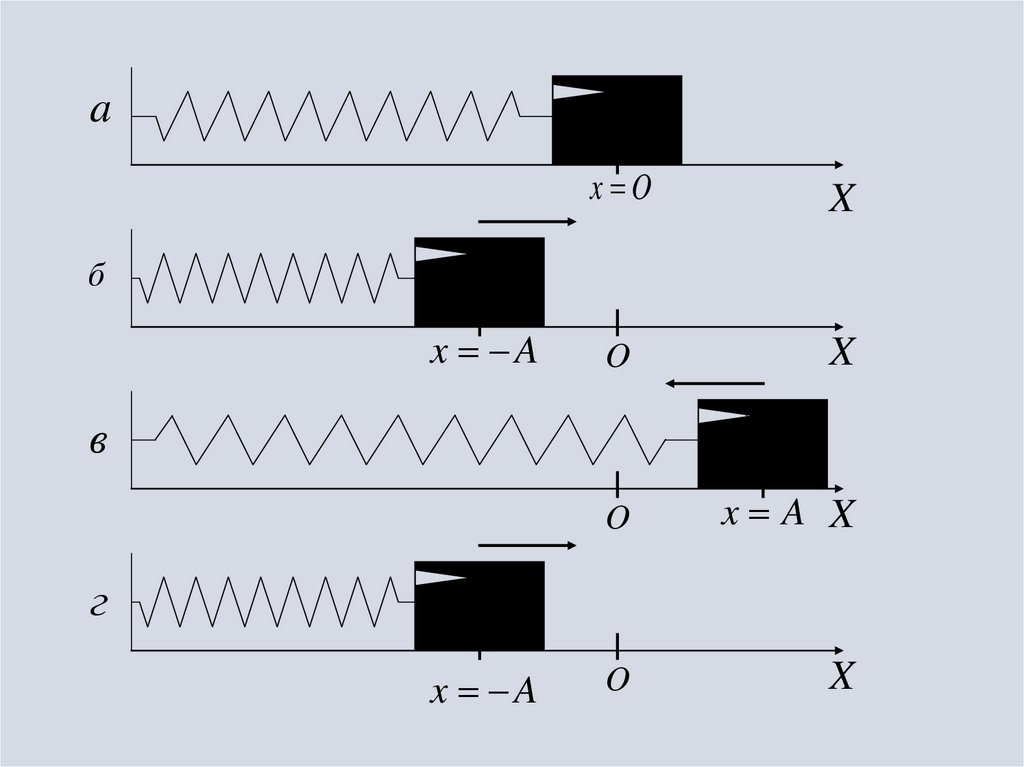
18.

a
x O
X
O
X
O
x A X
O
X
б
x A
в
г
x A

19.

Преобразование энергии при
гармонических колебаниях
При гармонических колебаниях периодически
происходит переход потенциальной энергии в
кинетическую и обратно. При движении тела к
положению равновесия его потенциальная энергия
убывает, а кинетическая возрастает. В момент
прохождения телом положения равновесия его
потенциальная энергия минимальна, а кинетическая
энергия максимальна.
Полная механическая энергия системы W Wk Wп,
где W - кинетическая энергия, Wп - потенциальная
энергия.
k

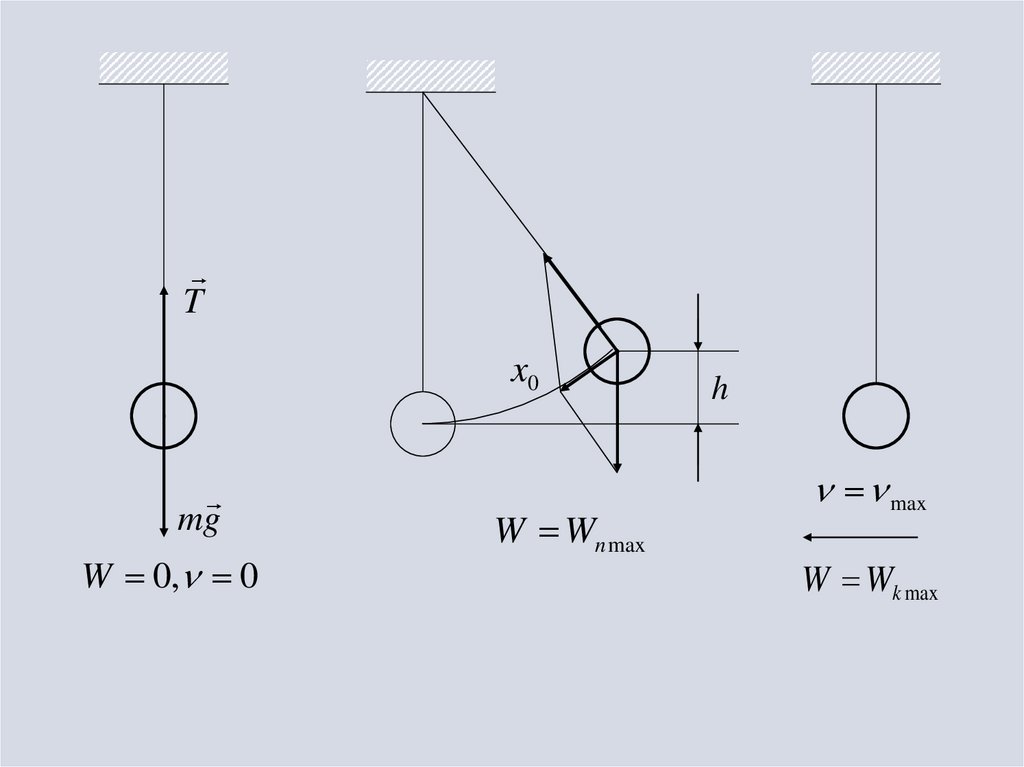
20.

T
x0
mg
W 0, 0
W Wn max
h
max
W Wk max

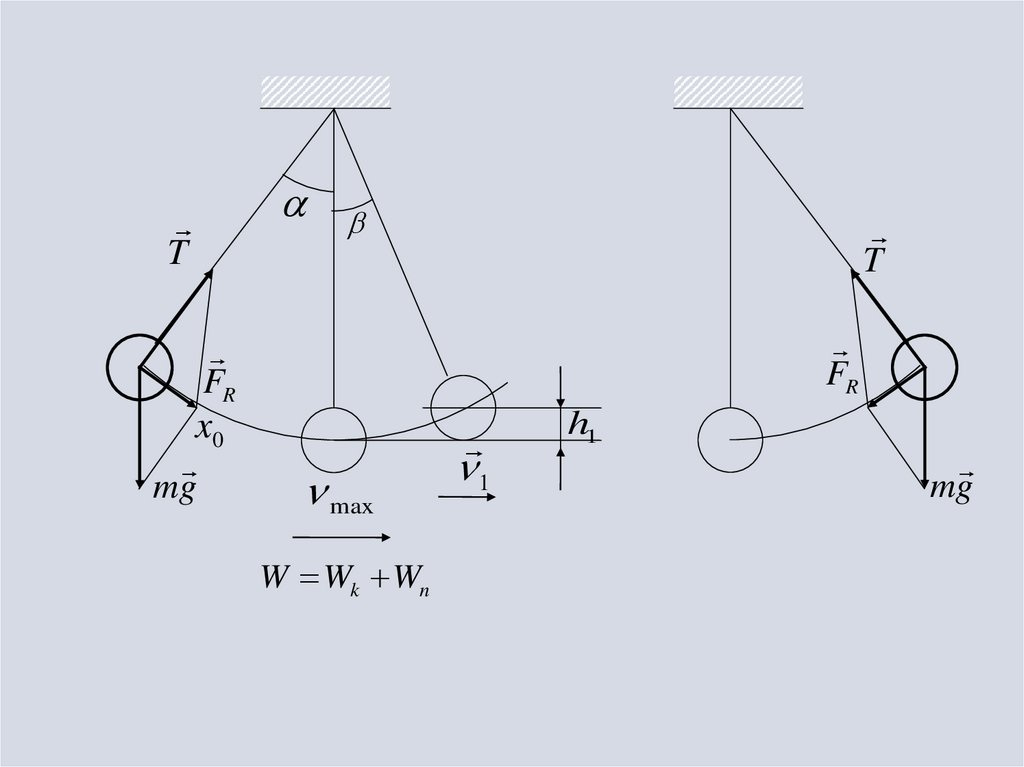
21.

T
T
FR
FR
x0
mg
max
W Wk Wn
1
h1
mg

22.

Для пружинного маятника в момент прохождения телом
2
mvmax W 0
положения равновесия W Wk max
,
;
п
2
kA2
В крайних точках W Wп max
, Wk 0 ;
2
m 2 kx2
в промежуточных точках W
.
2
2
Если колебания тела происходят по закону x A sin( t 0 )
то кинетическая энергия тела равна:
m x
mA 2 2 cos 2 ( t 0 )
Wk
2
2
2

23.

Потенциальная энергия тела равна:
kx2 kA2 sin 2 ( t 0 )
Wп
2
2
2
k
m
Так как
,то
m 2 A2 sin 2 ( t 0 )
Wп
2
За нулевой уровень отсчета потенциальной энергии
выбирается положение равновесия тела (x=0).
Полная механическая энергия системы равна:
m 2 A 2
W0 Wk Wп
2