Свойства дерева: единственность пути, существование висячей вершины, связь между числом вершин и числом рёбер

1.

Свойства дерева: единственность
пути, существование висячей
вершины, связь между числом
вершин и числом рёбер

2.

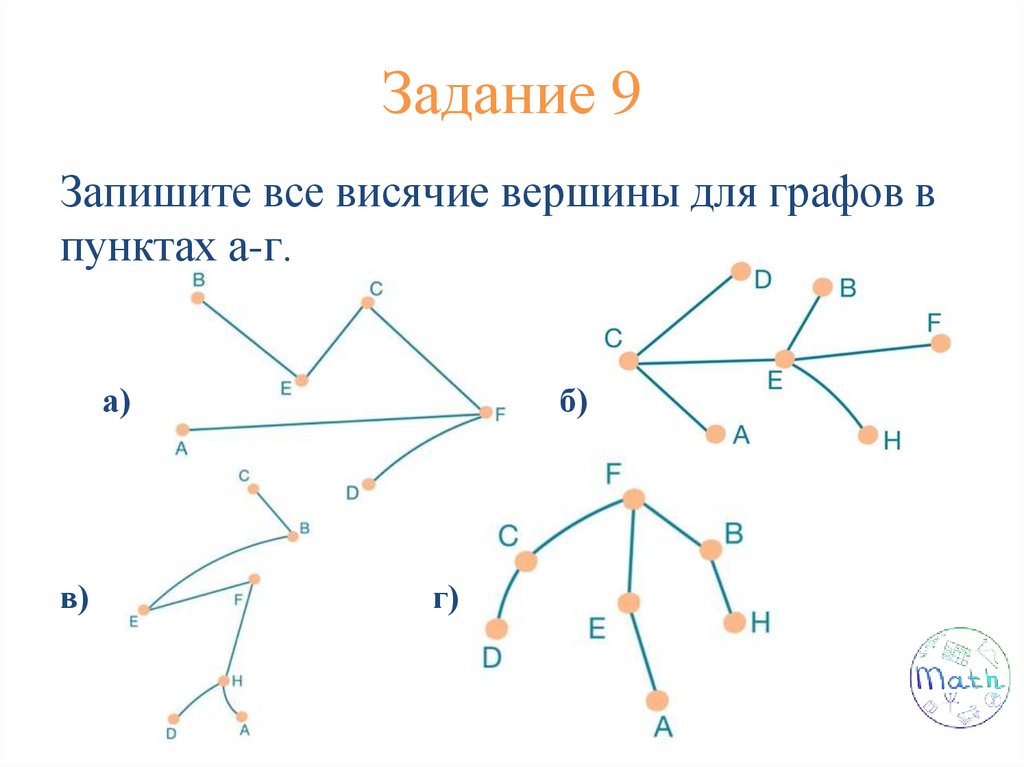
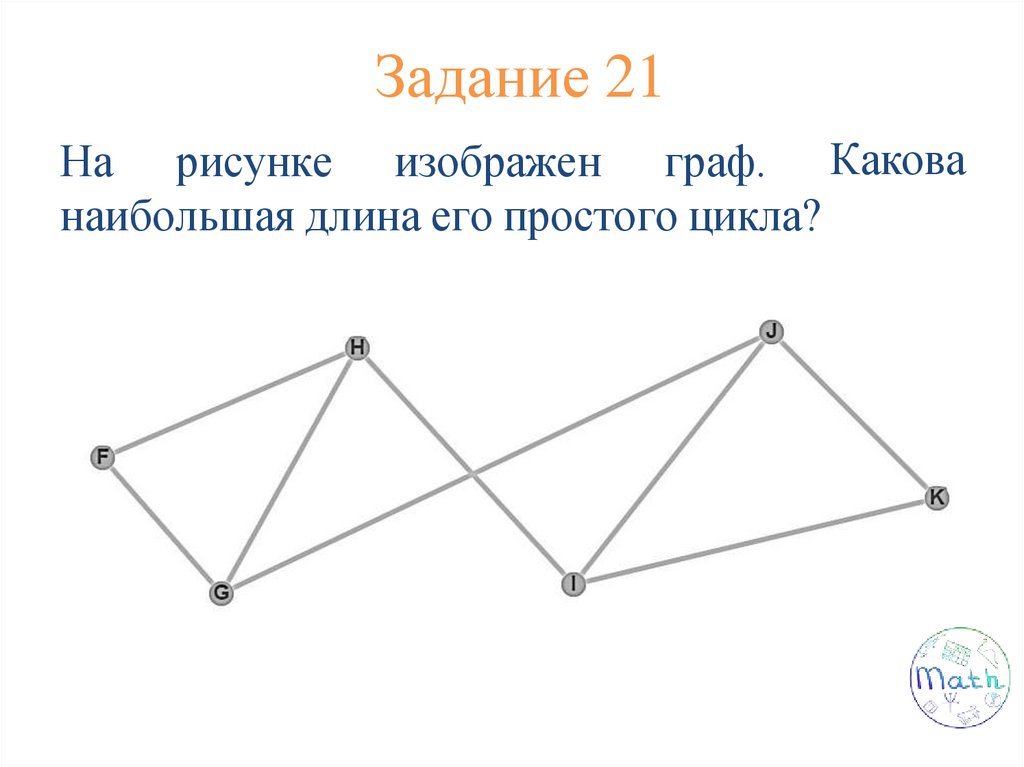
Задание 1

3.

Задание 1
Распределите утверждения на две группы: верно,
неверно.
a) Графом называется множество точек, некоторые из
которых могут быть соединены линиями.
b) Две вершины, которые являются соседними,
называются смежными вершинами.
c) Два ребра, у которых две общие вершины,
называются смежными ребрами.
d) Вершина, из которой не выходит ни одно ребро,
называется изолированной.
e) Путь называется цепью, если в нём не
повторяются вершины.
f) Простым циклом в графе называется цепь, у
которой начало и конец совпадают.

4.

Задание 1
g) Путем в графе от вершины А до вершины F называется
последовательность ребер графа и его вершин, такие,
что каждые два последовательных ребра имеют общую
вершину, и никакое ребро не встречается более двух
раз.
h) Циклом называется граф, который является цепью и у
него не совпадают начало и конец.
i) Граф называется связным, если для любой его
вершины найдется путь, связывающий ее с любой
другой вершиной этого графа.
j) Количество вершин в пути называется длиной этого
пути.
k) Граф, состоящий из двух изолированных вершин,
также является деревом.
l) Деревом называется всякий связный граф, не
имеющий циклов.

5.

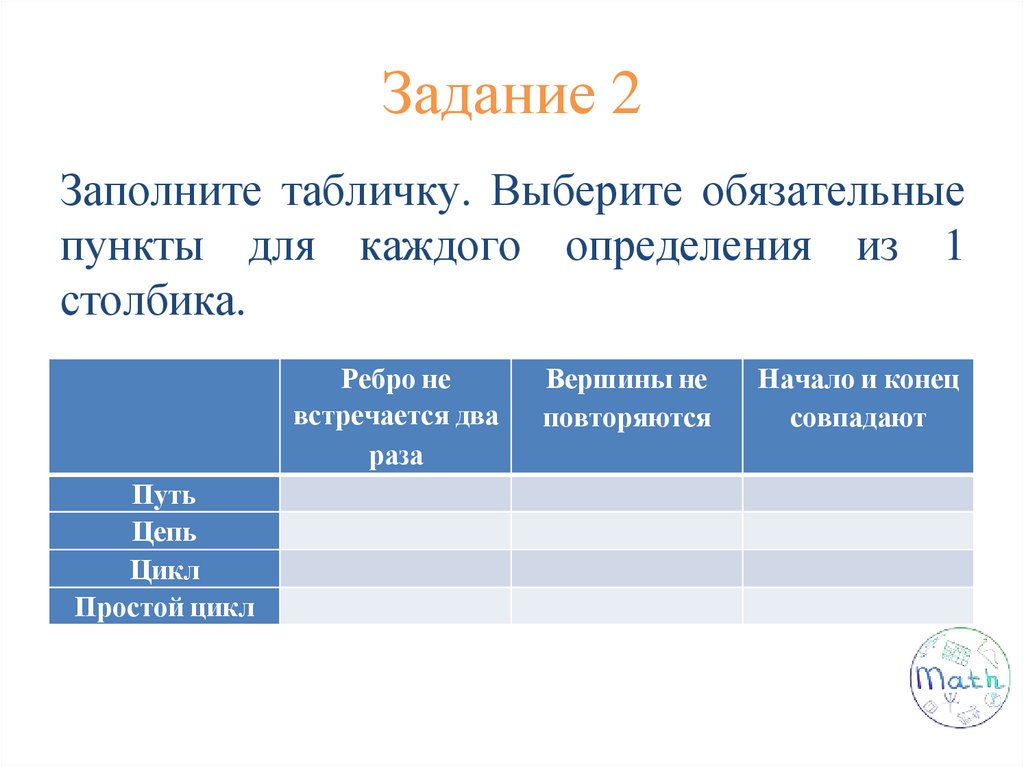
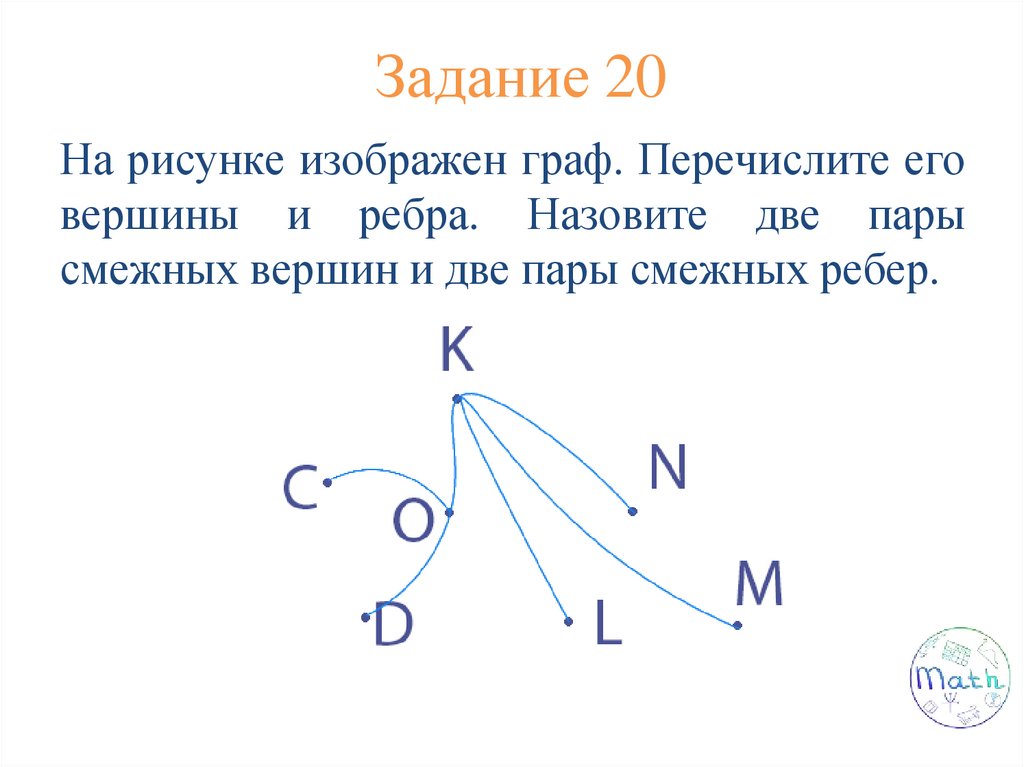
Задание 2
Заполните табличку. Выберите обязательные
пункты для каждого определения из 1
столбика.
Ребро не
встречается два
раза
Путь
Цепь
Цикл
Простой цикл
Вершины не
повторяются
Начало и конец
совпадают

6.

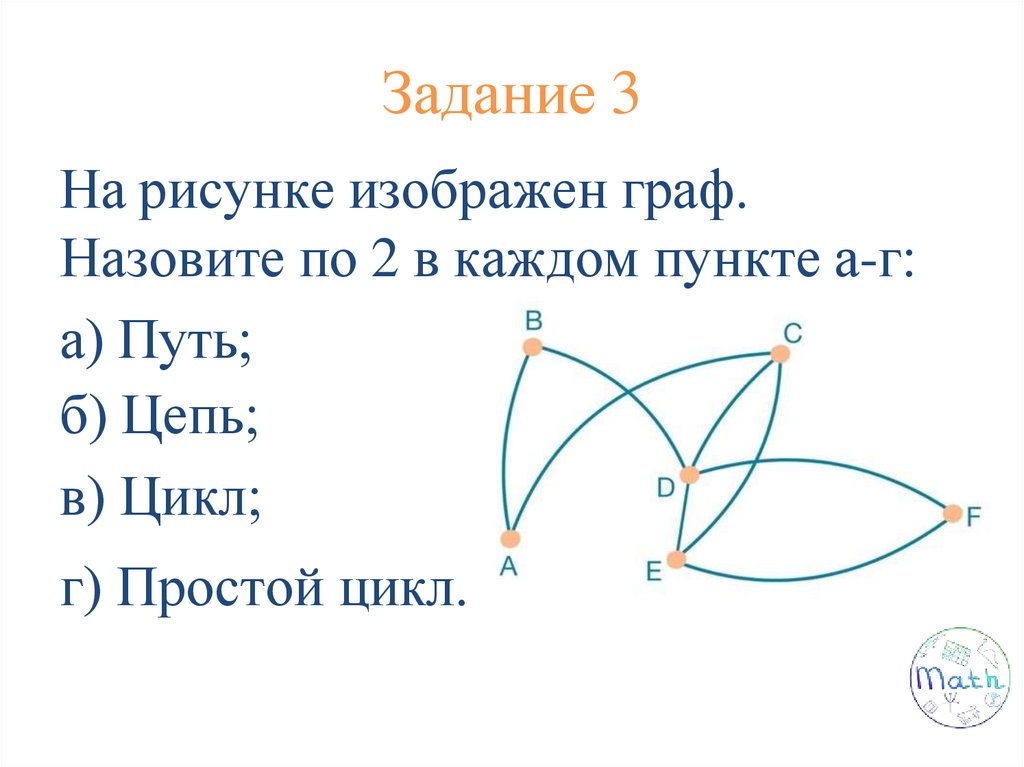
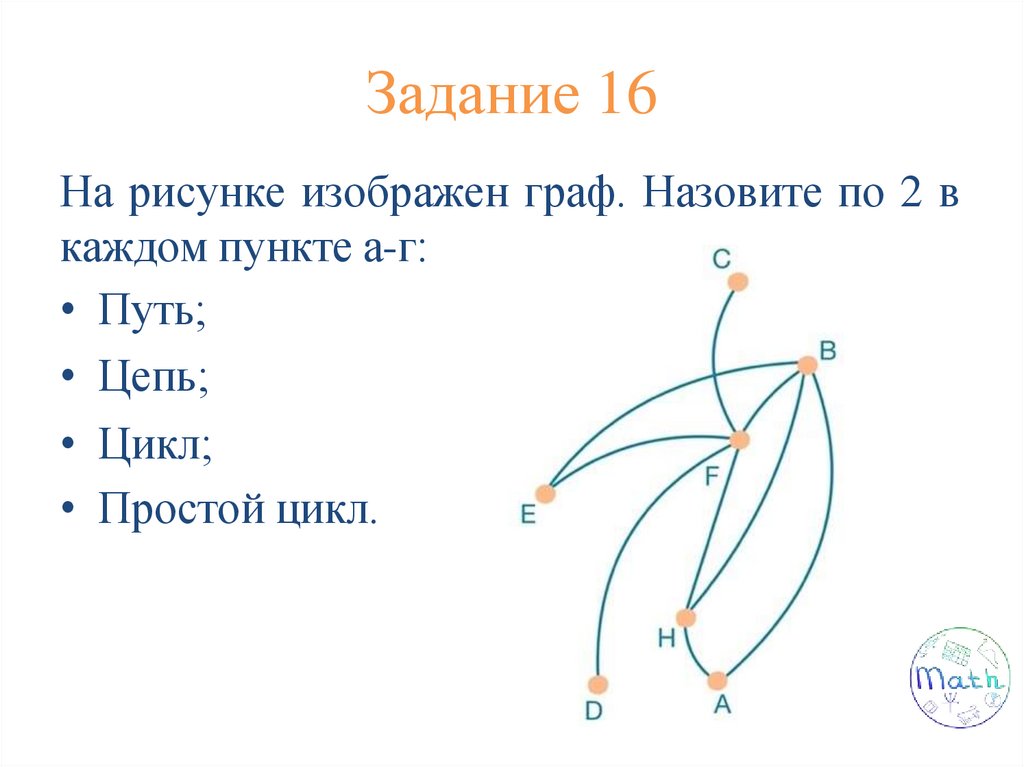
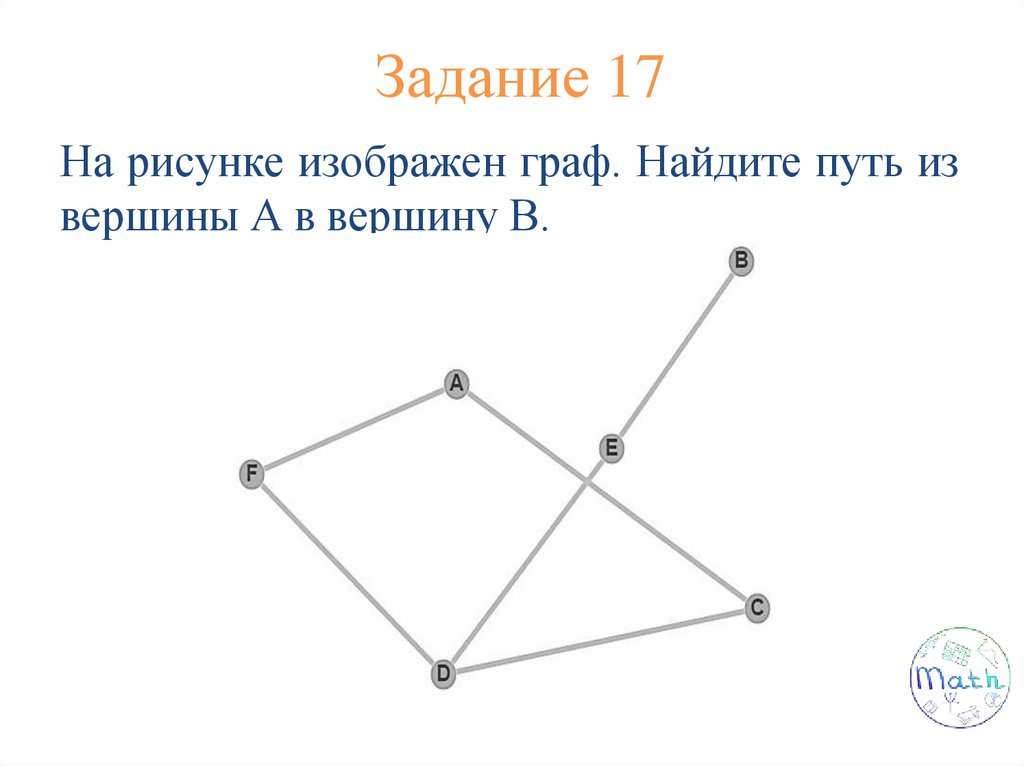
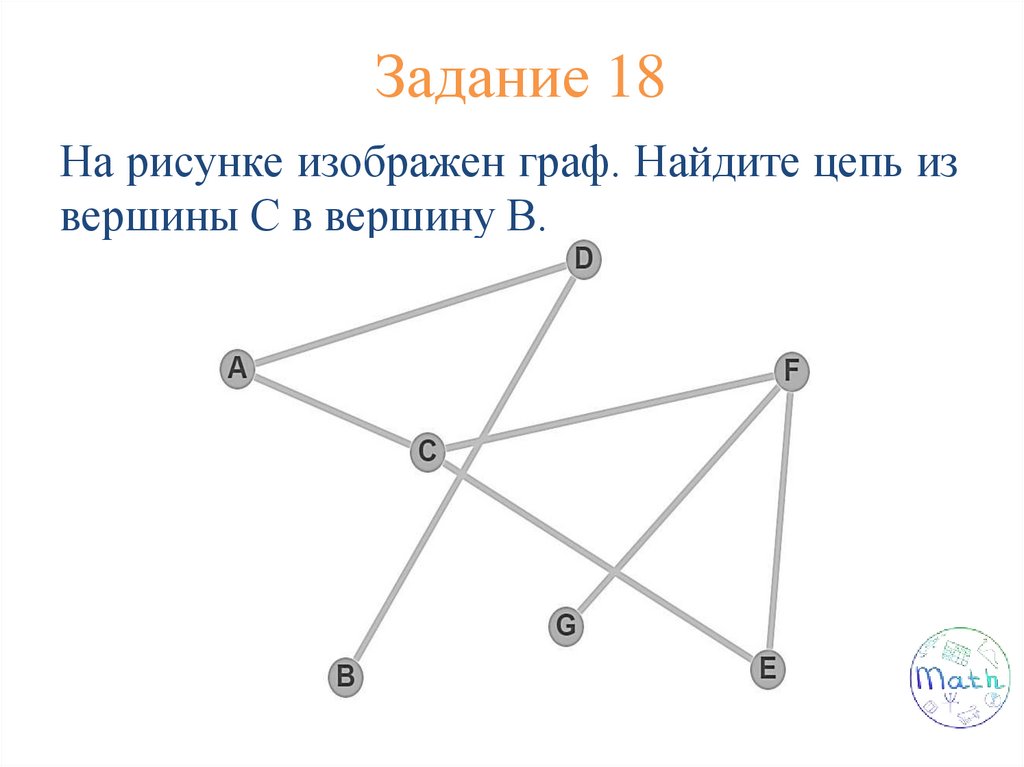
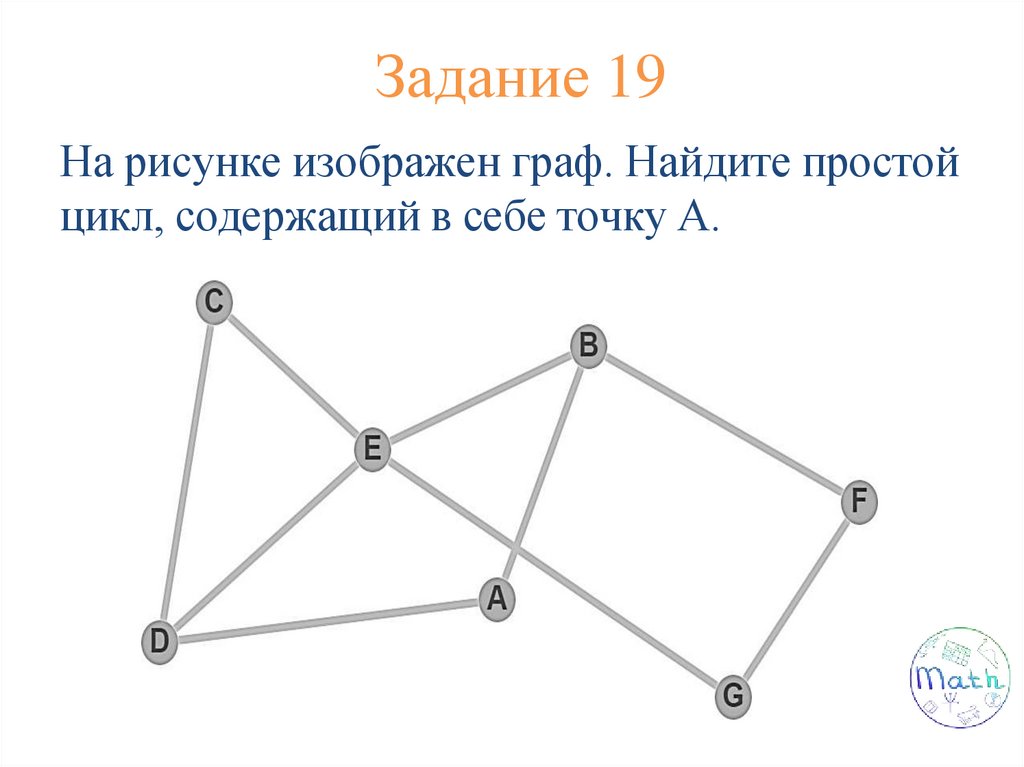
Задание 3
На рисунке изображен граф.
Назовите по 2 в каждом пункте а-г:
а) Путь;
б) Цепь;
в) Цикл;
г) Простой цикл.

7.

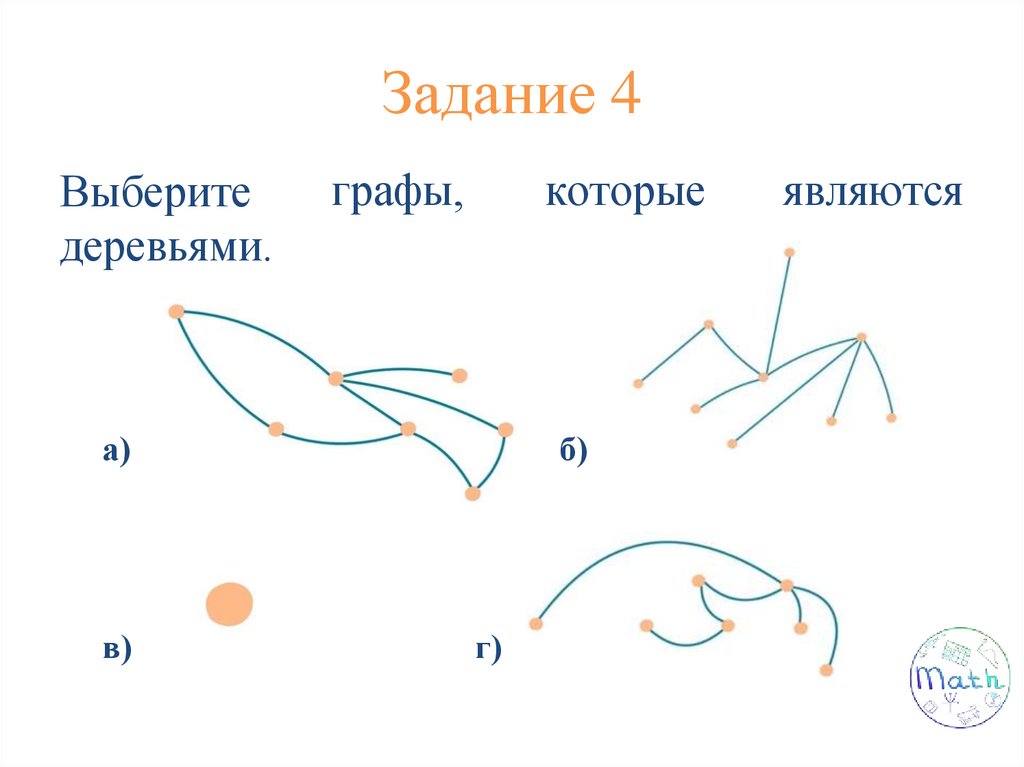
Задание 4
Выберите
деревьями.
графы,
которые
а)
в)
б)
г)
являются

8.

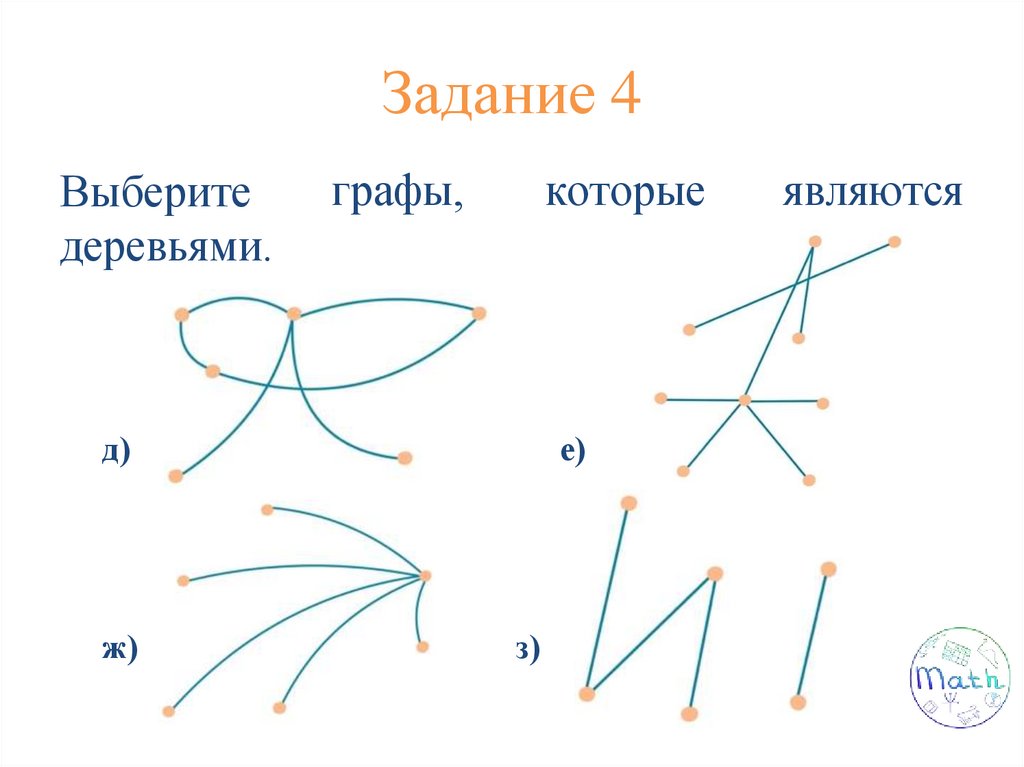
Задание 4
Выберите
деревьями.
графы,
которые
д)
ж)
е)
з)
являются

9.

Степенью (валентностью или порядком)
вершины называется количество ребер,
исходящих из этой вершины.
Вершина называется четной, если из нее
выходит четное количество ребер.
Вершина называется нечетной, если из нее
выходит нечетное количество ребер.

10.

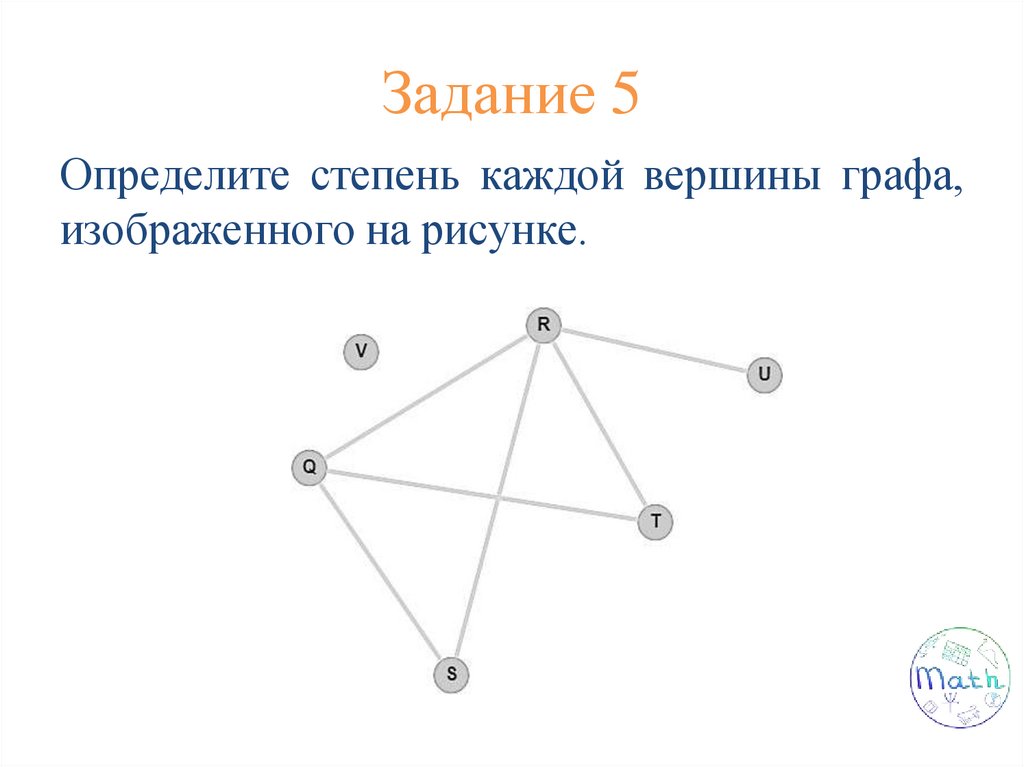
Задание 5
Определите степень каждой вершины графа,
изображенного на рисунке.

11.

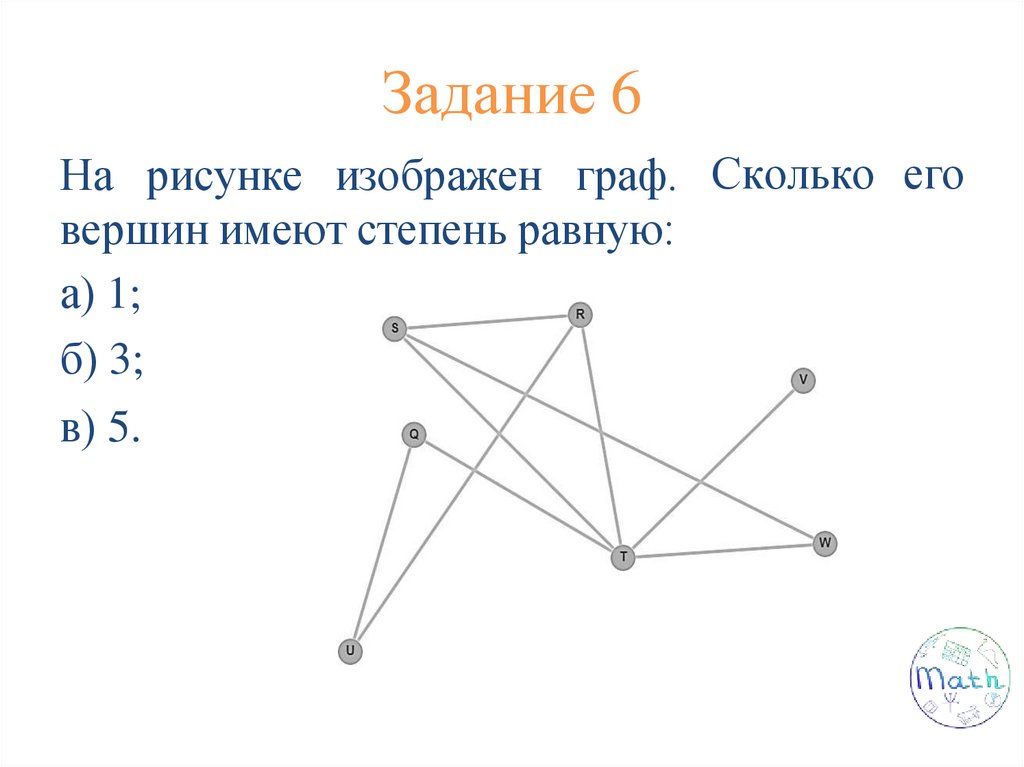
Задание 6
На рисунке изображен граф. Сколько его
вершин имеют степень равную:
а) 1;
б) 3;
в) 5.

12.

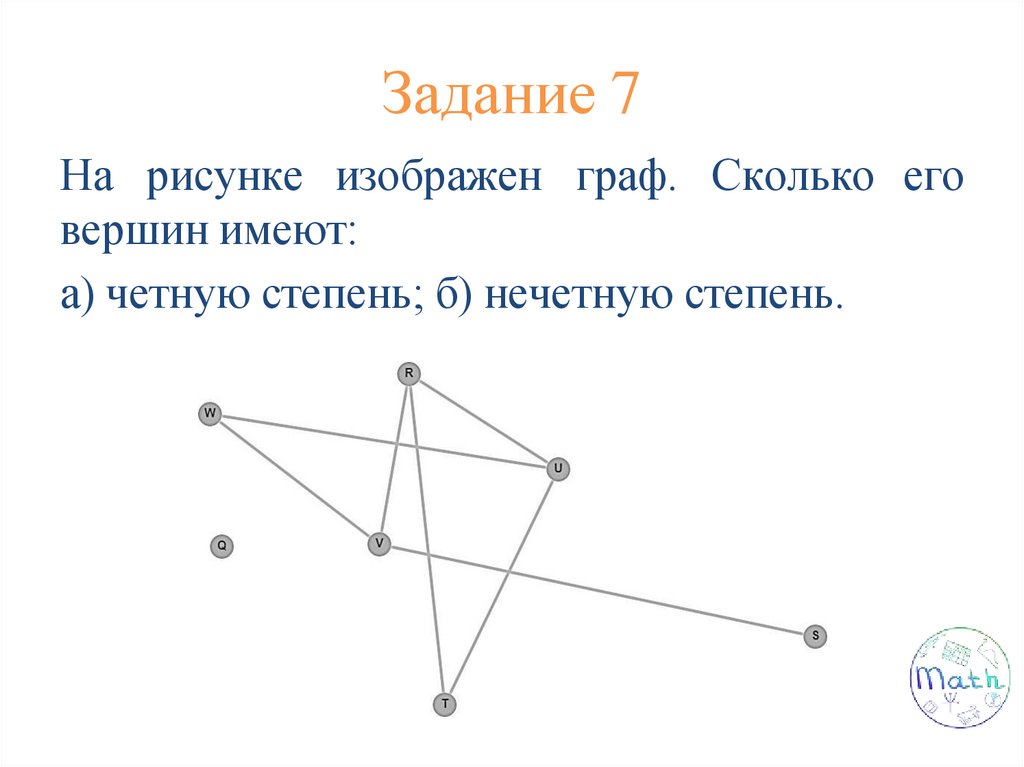
Задание 7
На рисунке изображен граф. Сколько его
вершин имеют:
а) четную степень; б) нечетную степень.

13.

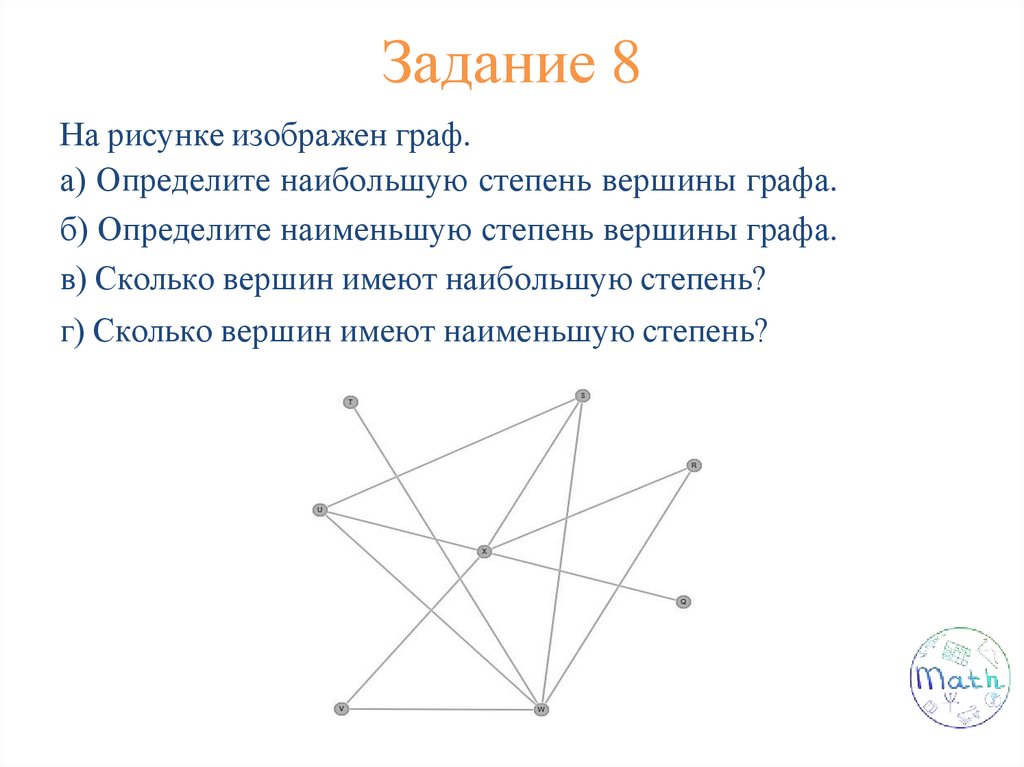
Задание 8
На рисунке изображен граф.
а) Определите наибольшую степень вершины графа.
б) Определите наименьшую степень вершины графа.
в) Сколько вершин имеют наибольшую степень?
г) Сколько вершин имеют наименьшую степень?

14.

Теорема 1
любыми
двумя
Между
вершинами дерева существует
единственный путь, который
их соединяет.

15.

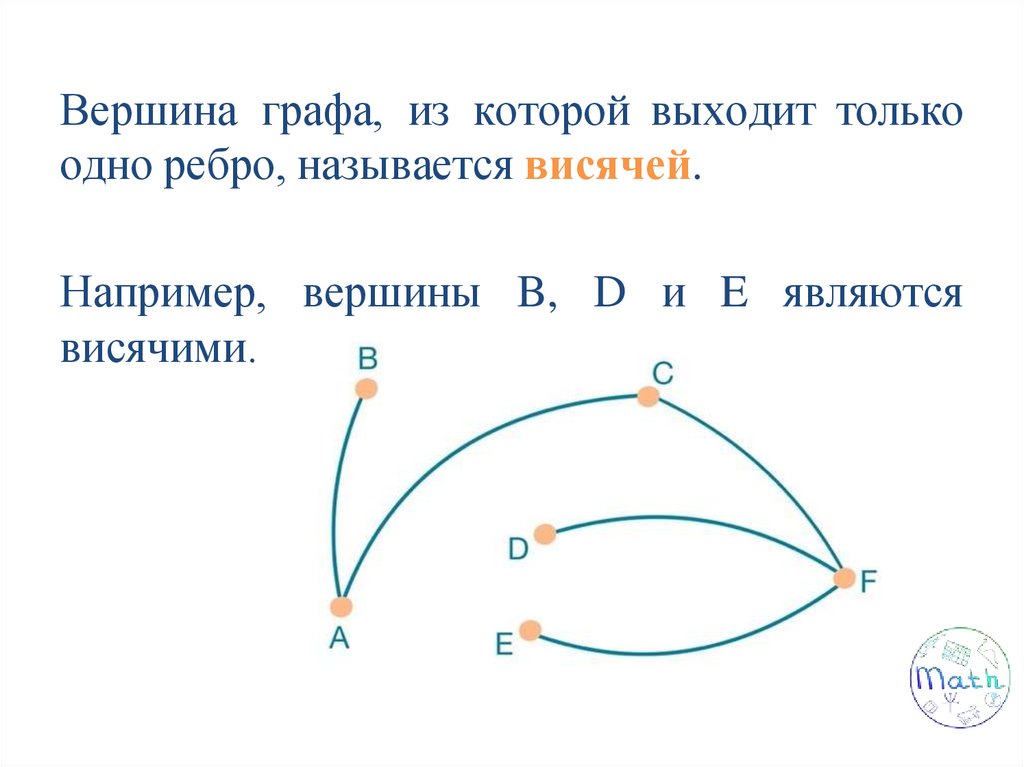
Вершина графа, из которой выходит только
одно ребро, называется висячей.
Например, вершины B, D и E являются
висячими.

16.

Теорема 2
В любом дереве (в котором
более одной вершины) есть
вершина, из которой выходит
ровно
одно
ребро,
т.е.
вершина является висячей.

17.

Теорема 3
В дереве количество вершин на 1
больше количества рёбер, то есть