Роль математики в 3D - дизайне

1.

Зайцев Даниил Дмитриевич
Руководитель: Маковская Ольга Михайловна

2.

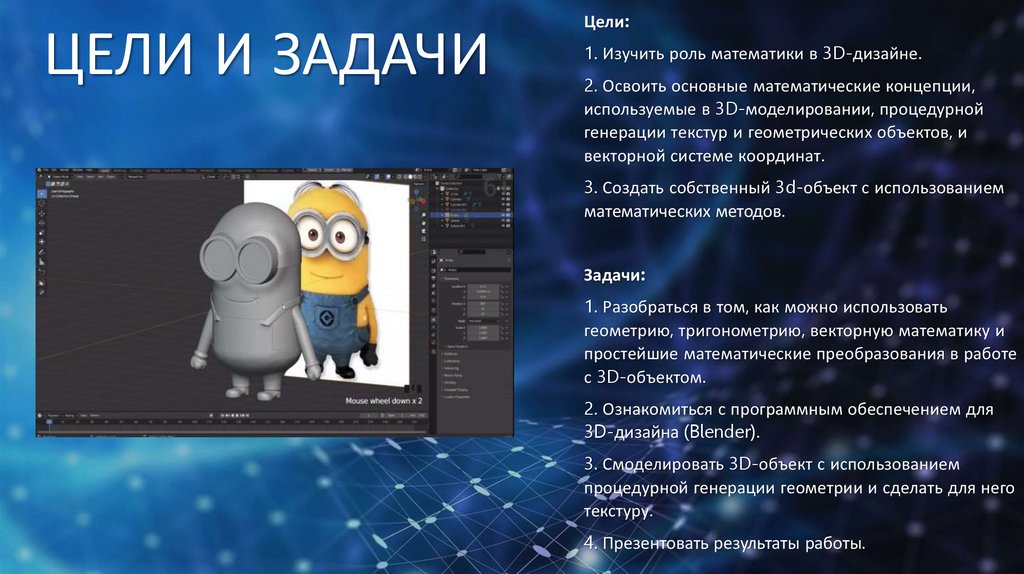
ЦЕЛИ И ЗАДАЧИ
Цели:
1. Изучить роль математики в 3D-дизайне.
2. Освоить основные математические концепции,
используемые в 3D-моделировании, процедурной
генерации текстур и геометрических объектов, и
векторной системе координат.
3. Создать собственный 3d-объект с использованием
математических методов.
Задачи:
1. Разобраться в том, как можно использовать
геометрию, тригонометрию, векторную математику и
простейшие математические преобразования в работе
с 3D-объектом.
2. Ознакомиться с программным обеспечением для
3D-дизайна (Blender).
3. Смоделировать 3D-объект с использованием
процедурной генерации геометрии и сделать для него
текстуру.
4. Презентовать результаты работы.

3.

АКТУАЛЬНОСТЬ ПРОЕКТА
1. Растущий интерес к 3D-дизайну в
индустрии видеоигр, кино и архитектуры.
2. Актуальность навыков 3D-моделирования в
образовательных и профессиональных сферах.
3. Необходимость понимания математических
основ для успешной работы с современными
технологиями.

4.

История создания первой программы для 3Dмоделирования:
Айвен Сазерленд, американский учёный и пионер в области компьютерной графики, в
1963 году сделал огромный шаг в развитии 3D моделирования. В то время он был
аспирантом в Массачусетском технологическом институте (MIT) и работал над своей
диссертацией.
Сазерленд начал исследовать возможности визуализации данных и, используя свой
опыт, разработал программу под названием "Sketchpad". Эта программа позволила
пользователям создавать изображения и модели на экране, используя графический
интерфейс. С помощью Sketchpad Айвен продемонстрировал, как можно
манипулировать объектами в двумерном пространстве, что стало основой для
дальнейшей разработки трехмерной графики.
Вдохновение пришло к нему, когда он изучал архитектурные проекты и рисование. Он
осознал, что возможность визуализировать объекты в 3D может значительно упростить
процесс проектирования. Как следствие, его работа положила начало новым подходам
в архитектуре, инженерии и дизайне.
Ключевым моментом в его исследованиях стало создание концепции использования
преобразований объектов, таких как вращение и масштабирование, что обеспечивало

5.

История зарождения текстурирования 3Dмоделей:
В начале 1970-х годов начали появляться первые работы в области текстурирования,
когда ученые и разработчики начали применять алгоритмы для создания текстур и их
наложения на 3D-объекты. Одним из первых методов текстурирования был метод
"базового цвета", который использовался для придания поверхностям цвета, но не имел
сложных деталей.
В 1980-х годах текстурирование стало более распространенным в игровой индустрии и
анимации. Появление новых технологий, таких как графические процессоры (GPU),
дало возможность более детализированного текстурирования. Такие компании, как
Pixar и Industrial Light & Magic, сыграли важную роль в разработке технологий и
методов текстурирования, что позволило создавать более реалистичные 3D-модели.
С течением времени стали развиваться более сложные методы, такие как bump
mapping и normal mapping, которые добавляют глубину и детализацию на
поверхность объектов, при этом не затрагивая саму геометрию объекта. Также
появилась технология, позволяющая делать часть объекта прозрачной или
полупрозрачной, альфа канал. В 1990-х и 2000-х годах текстурирование стало
стандартной практикой в 3D-моделировании, а различные программные пакеты, такие
как Blender, Maya и 3ds Max, начали предлагать встроенные инструменты для

6.

Трансформация 3-мерных объектов:
В любой программе для 3D-моделирования с
объектами можно производить различные
трансформации: Менять их размер, менять их
положение в пространстве, а также вращать объекты
и менять их центр вращения. Все эти трансформации
можно осуществлять по трём осям: x, y, z. За все эти
параметры отвечает математика, так как они
регулируются числами, расстояние высчитывается в
метрах, вращение в градусах. Так же окно для
трансформации в программе Blender поддерживает
математические выражения. Значения можно
складывать, вычитать, умножать и т.д. Также все эти
параметры можно анимировать, чтобы они менялись
в течение определённого времени. В Blender
покадровая анимация, а количество кадров в секунду
можно регулировать в настройках рендера. Также
различные параметры можно связывать между
собой. Например - связать перемещение между
двумя объектами, чтобы 1 объект перемещался туда
же, куда перемещается другой. Благодаря этой
механике можно создавать сложные и красивые
сцены.

7.

Анимация объектов с помощью
тригонометрии:
Если заменить масштаб по оси x на выражение
sin(frame/10)*2 масштаб объекта по оси x будет
равен синусу от frame ( переводится с английского,
как кадр ), делённого на 10, умноженному на 2
каждый кадр. То есть каждый кадр значение будет
разным, и из-за этого получится циклическая
анимация того, как объект растягивается и сжимается
обратно. Цикличность получится из-за синуса в
выражении, его значение будет скакать от 1 до -1 и
обратно, так как кадр сменяется равномерно ( В этом
случае Blender считывает кадры в радианах, а не
градусах ). Умножение синуса на 2 позволит
растягивать объект в 2 раза больше, а деление кадра
на 10, сделает анимацию медленнее.

8.

Геометрия в 3д-моделировании:
Любой 3D объект имеет свой меш, меш – это форма
объекта. У двух разных объектов может быть один и тот
же меш. Меш имеет структуру обычной геометрической
фигуры. Он состоит из точек, рёбер и граней, которые
можно трансформировать (менять размер, вращать и
перемещать) и присоединять друг к другу, также их
можно экструдировать (создавать новые точки, рёбра и
грани методом выдавливания). В этом и заключается вся
суть моделирования объекта. Также в 3D-моделировании
есть такое понятие, как нормаль. Нормаль – это вектор,
перпендикулярный плоскости полигона, который
указывает, куда ему отражать свет. Направлен этот
вектор только в одну сторону. Нормали можно
сглаживать, создавая элюзию того, что меш объекта
гладкий. Силу сглаживания в Blender можно изменять,
увеличивая или уменьшая число градусов угла наклона
нормали, которые подвергаются сглаживанию.

9.

ВЕКТОРНАЯ МАТЕМАТИКА В 3Д
Векторная математика – это раздел математики,
изучающий векторы. Векторы представляют собой
математические объекты, имеющие величину и
направление. В процедурной генерации текстур с
помощью векторов можно задавать координаты
расположения текстуры на объекте. Любая модель
имеет UV-развёртку, которая позволяет корректно
отображать 2D текстуры на 3D модели. Благодаря
векторным координатам можно перемещать
текстуру относительно UV-развёртки.

10.

Векторная математика в процедурной
генерации текстур 1 :
В программе Blender благодаря материальным нодам, системе
для создания текстур и шейдеров (Шейдеры отвечают за
взаимодействие объектов со светом), можно производить
различные математические преобразования с тремя значениями
вектора: x, y, z. Это делается с помощью нода VectorMath, эта
функция позволяет совершать любые математические действия с
векторными значениями.
Vector Math

11.

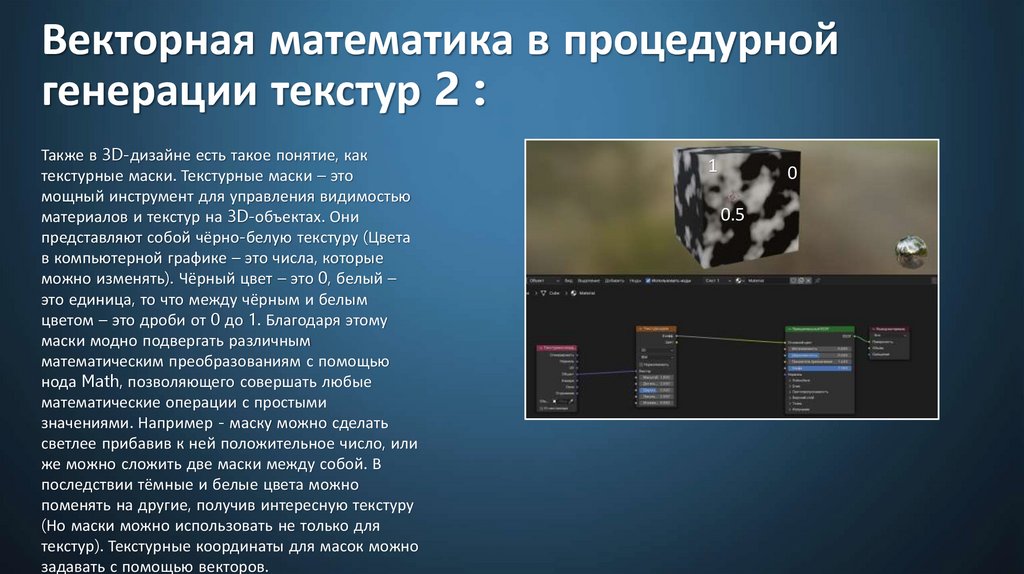
Векторная математика в процедурной
генерации текстур 2 :
Также в 3D-дизайне есть такое понятие, как
текстурные маски. Текстурные маски – это
мощный инструмент для управления видимостью
материалов и текстур на 3D-объектах. Они
представляют собой чёрно-белую текстуру (Цвета
в компьютерной графике – это числа, которые
можно изменять). Чёрный цвет – это 0, белый –
это единица, то что между чёрным и белым
цветом – это дроби от 0 до 1. Благодаря этому
маски модно подвергать различным
математическим преобразованиям с помощью
нода Math, позволяющего совершать любые
математические операции с простыми
значениями. Например - маску можно сделать
светлее прибавив к ней положительное число, или
же можно сложить две маски между собой. В
последствии тёмные и белые цвета можно
поменять на другие, получив интересную текстуру
(Но маски можно использовать не только для
текстур). Текстурные координаты для масок можно
задавать с помощью векторов.
1
0
0.5

12.

Фейковая геометрия с помощью масок:
Ещё маски можно использовать для
создания фейковой геометрии на
объекте, для этого её нужно подключить
в нод Bumb, а этот нод в любой шейдер,
в котором есть параметр нормаль.
Принцип простой, более светлые
значения выпирают в одну сторону,
более тёмные в другую. Также можно
использовать встроенные в программу
процедурные чёрно-белые текстуры и
регулировать их.
Bump

13.

Процедурная генерация геометрии:
Помимо материальных нодов,
существуют геометрические.
Они отвечают за генерацию
геометрии. В них можно
выполнять различные
математические операции с
параметрами трансформации
объекта (Размер, вращение,
положение) с помощью
векторной математики. Также
геометрические ноды
позволяют менять форму меша.
Например – если накинуть
процедурную чёрно-белую
текстуру шума на перемещение
плоскости с большим
количеством подразделений по
оси z, то точки плоскости
распределятся по оси z в
случайном порядке. Получится

14.

PYTHON В BLENDER
Также для автоматизации рабочего процесса можно
использовать программирование. В программе
Blender
можно
использовать
язык
программирования Python. Благодаря нему можно
удобно анимировать объекты, переименовывать и
проделывать
другие
действия
с
большим
количеством объектов за один клик. В следствии
этого для программы создано множество адонов
(Дополнений, упрощающих рабочий процесс), их
можно создавать самостоятельно, используя всё тот
же Python.

15.

ПЕРЕЙДЁМ К
ПРАКТИЧЕСКОЙ
ЧАСТИ