Симплексный метод решения ЗЛП

1.

Симплексный метод решения ЗЛП
Симплексный метод – это аналитический метод решения ЗЛП, реализующий алгоритм графического метода
аналитически, без построения чертежа.
Метод является универсальным, так как позволяет решить практически любую задачу линейного
программирования, записанную в каноническом виде.
Математическая модель задачи ЛП может быть канонической и неканонической.
Определение. Если все ограничения системы заданы уравнениями и переменные xj неотрицательные, то такая
модель задачи называется канонической.
Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической.
Чтобы перейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую
переменную.
Если знак неравенства ≤, то балансовая переменная вводится со знаком плюс,
если знак неравенства ≥, то — минус.
В целевую функцию балансовые переменные не вводятся.
Слайд 25

2.

Алгоритм решения ЗЛП симплексным методом
1. Математическая модель задачи должна быть канонической. Если она неканоническая, то ее надо
привести к каноническому виду.
2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем
симплексную таблицу (таблица). Все строки таблицы 1-го шага, за исключением строки Δj (индексная
строка), заполняем по данным системы ограничений и целевой функции.
+
Индексная строка для переменных находится по формуле
и по формуле
для свободного члена.
Слайд 26

3.

Возможны следующие случаи при решении задачи на максимум:
— если все оценки
то найденное решение оптимальное;
— если хотя бы одна оценка
но при соответствующей переменной нет ни одного
положительного коэффициента, решение задачи прекращаем, так как, целевая функция неограничена в
области допустимых решений;
— если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один
положительный коэффициент, то нужно перейти к другому опорному решению;
— если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП)
вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная
оценка.
Если хотя бы одна оценка
то k-й столбец принимаем за ключевой.
За ключевую строку принимаем ту, которой соответствует минимальное отношение свободных
членов (bi) к положительным коэффициентам k-гo столбца.
Элемент, находящийся на пересечении ключевых строки и столбца, называется ключевым элементом.
3. Заполняем симплексную таблицу 2-го шага:
— переписываем ключевую строку, разделив ее на ключевой элемент;
— заполняем базисные столбцы;
+— остальные коэффициенты таблицы находим по правилу "прямоугольника". Оценки можно считать по
приведенным выше формулам или по правилу "прямоугольника" Получаем новое опорное решение,
которое проверяем на оптимальность, и т.д.
Слайд 27

4.

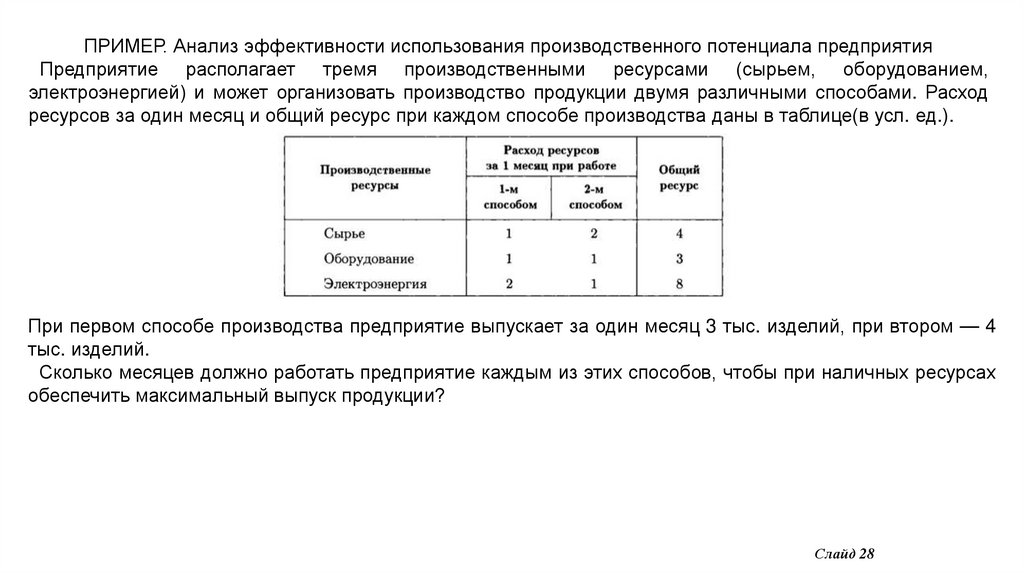
ПРИМЕР. Анализ эффективности использования производственного потенциала предприятия
+Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием,
электроэнергией) и может организовать производство продукции двумя различными способами. Расход
ресурсов за один месяц и общий ресурс при каждом способе производства даны в таблице(в усл. ед.).
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором — 4
тыс. изделий.
+Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах
обеспечить максимальный выпуск продукции?
Слайд 28

5.

Решение. Составим математическую модель задачи. Обозначим: x1 — время работы предприятия
первым способом, x2 — время работы предприятия вторым способом.
Математическая модель имеет вид
при ограничениях:
Приведем задачу к каноническому виду:
При ограничениях:
Слайд 29

6.

Составляем симплексную таблицу 1-го шага
В индексной строке Δj имеются две отрицательные оценки, значит, найденное решение не является
оптимальным и его можно улучшить.
В качестве ключевого столбца следует принять столбец базисной переменной х2, а за ключевую
строку взять строку переменной x3, где min (4/2,3/l, 8/1) = min (2, 3, 8) = 2.
Ключевым
элементом
является
(2).
Вводим
в
переменной х2, выводим х3. Составляем симплексную таблицу 2-го шага
столбец
базисной
Слайд 30

7.

В индексной строке имеется одна отрицательная оценка.
Полученное решение можно улучшить.
Ключевым элементом является (1/2).
Составляем симплексную таблицу 3-го шага
Все оценки свободных
переменных Δj ≥ 0,
найденное опорное решение
является оптимальным:
Таким образом, по первому способу предприятие должно работать два месяца, по второму — один месяц,
при этом максимальный выпуск продукции составит 10 тыс. ед.
Слайд 31

8.

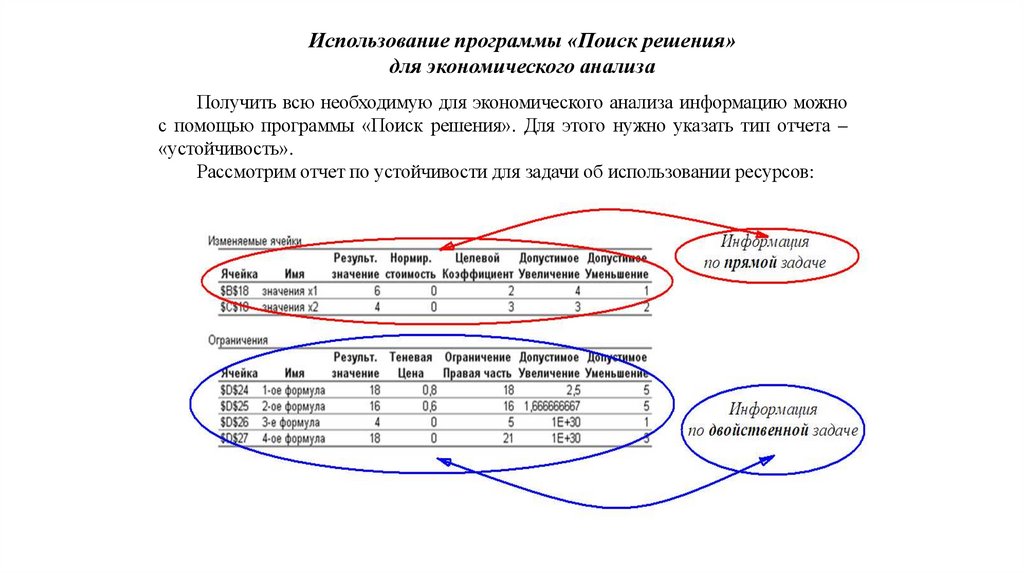
Использование программы «Поиск решения»
для экономического анализа
Получить всю необходимую для экономического анализа информацию можно
с помощью программы «Поиск решения». Для этого нужно указать тип отчета –
«устойчивость».
Рассмотрим отчет по устойчивости для задачи об использовании ресурсов:

9.

Верхняя часть таблицы содержит информацию, относящуюся к переменным.
«результ. значение» - найденные оптимальные значения переменных Х*.
«нормир. стоимость» - непроизводительные затраты. Для рентабельных видов
продукции они равны нулю. Для нерентабельных величина нормированной
стоимости показывает, на сколько изменится целевая функция в случае
принудительного включения единицы такой продукции в план производства.
«целевой коэффициент» - коэффициенты целевой функции.
«допустимое увеличение» и «допустимое уменьшение» - предельные значения
приращений целевых коэффициентов, при которых сохраняется структура
оптимального плана прямой задачи.

10.

Во второй части таблицы содержится информация, относящаяся к ограничениям
«результ. значение» - величина затрат соответствующего ресурса при
реализации оптимального плана;
«теневая цена» - оптимальные значения двойственных переменных У*;
«ограничения правая часть» - запасы ресурсов;
«допустимое увеличение» и «допустимое уменьшение» - предельные
значения приращений ресурсов, при которых сохраняется структура
оптимального плана двойственной задачи.