Элементы кристаллофизики. Принципы кристаллофизики

1.

Тема 1.
Элементы кристаллофизики. Принципы кристаллофизики
Не́ йман Франц Эрнст
(1798-1895)
Начиная с 1878 г. Пьер вместе с братом Полем Жаном в
помещении минералогической лаборатории Сорбонны в течение
четырех лет проводили интенсивные экспериментальные работы
в области природы кристаллов.
Братья Кюри открыли пьезоэлектричество – появление под действием
приложенной извне силы на поверхности некоторых кристаллов
электрических зарядов.
Кристаллофизика изучает совокупность физических свойств кристаллов
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
Литература: 1. Сонин А.С. Беседы о кристаллофизики М.:Атомиздат,1976. 240 с.
2. Шаскольская М.П. Кристаллография. М.:Высш.шк.,1984. 376 с.
3. Сиротин Ю.И. , Шаскольская М.П. Основы кристаллофизики. М.:
Наука,1975.680с.

2.

1. Сонин А.С. Беседы о кристаллофизики М.:Атомиздат,1976. 240 с.
2. Шаскольская М.П. Кристаллография. М.:Высш.шк.,1984. 376 с.
3. Сиротин Ю.И. , Шаскольская М.П. Основы кристаллофизики. М.: Наука,1975.680с.
4. Най Дж. Физические свойства кристаллов / пер. Л.А. Шуваловой. М.:Из-во иностр.лит.,1960.386с.
5. Гуртов В.А., Осауленко Р.Н. Физика твердого тела для инженеров:
учеб.пособие.М.:Техносфера,2012.560с.
6. Павлов П.В., Хохлов А.Ф. Физика твердого тела.М.:ВШ,1985. 384 с.
7. Вустер У. Применение тензоров и теории групп для описания физических свойств кристаллов
/пер. Н.Р. Иванова. М.:Мир, 1977. 381с.
8. Шувалов Л.А., Урусовская А.А., Желудев И.С. идр. Современная кристаллография. M.:
Наука,1981.Т.4:Физические свойства кристаллов.496с.
9. Симонов В.И., Мальцев А.К. Структурная кристаллография // В мире науки.2005.№9.С.77–81.
10. Давыдов, В.Н. Материалы и элементы электронной техники. Часть 1.
Фундаментальные свойства кристаллических материалов: Учебное пособие. /
В.Н. Давыдов. Томск: Изд-во НТЛ, 2003, - 232 с.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024

3.

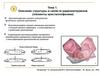
10)
Физические свойства кристаллов
Основное свойство всех кристаллов - анизотропия, т. е. зависимость
определяемого свойства от направления или симметрии структуры
кристалла, при этом симметрия структуры и симметрия физических свойств взаимосвязаны.
E
Внешний треугольник задает воздействие,
внутренний определяет отклик, пронумерованные связи
описывают возможные взаимосвязи и соответствующие свойства
2
9
D
10
5
4
15
7
14
X
1
T
12
13
8
S
11
6
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024
3
T
1- упругость
2- диэлектрическая проницаемость
3- теплоемкость
4- электромеханические эффекты
5 - электротермические эффекты
6 - термоупругие эффекты
7 - прямой пьезоэлектрический эффект
9 - обратный пьезоэлектрич. эффект
8 -пьезокалорический эффект
10- электрокалорический эффект
11 - тепловое расширение
12 - пироэлектрический эффект
13 - теплота поляризации
14 - теплота деформации
15 - электрострикция

4.

11)
Принципы кристаллофизики
Симметрия физических свойств кристалла связанна с его точечной группой симметрии.
Эта связь устанавливается фундаментальным законом кристаллофизики, известным под
названием принципа Неймана:
Принцип Неймана - постулат, устанавливающий связь симметрии макроскопических
физических свойств кристалла с симметрией его внешней формы.
Согласно этому принципу, группа симметрии любого спонтанно присущего
кристаллу физического свойства должна включать в себя операции симметрии
точечной группы симметрии кристалла
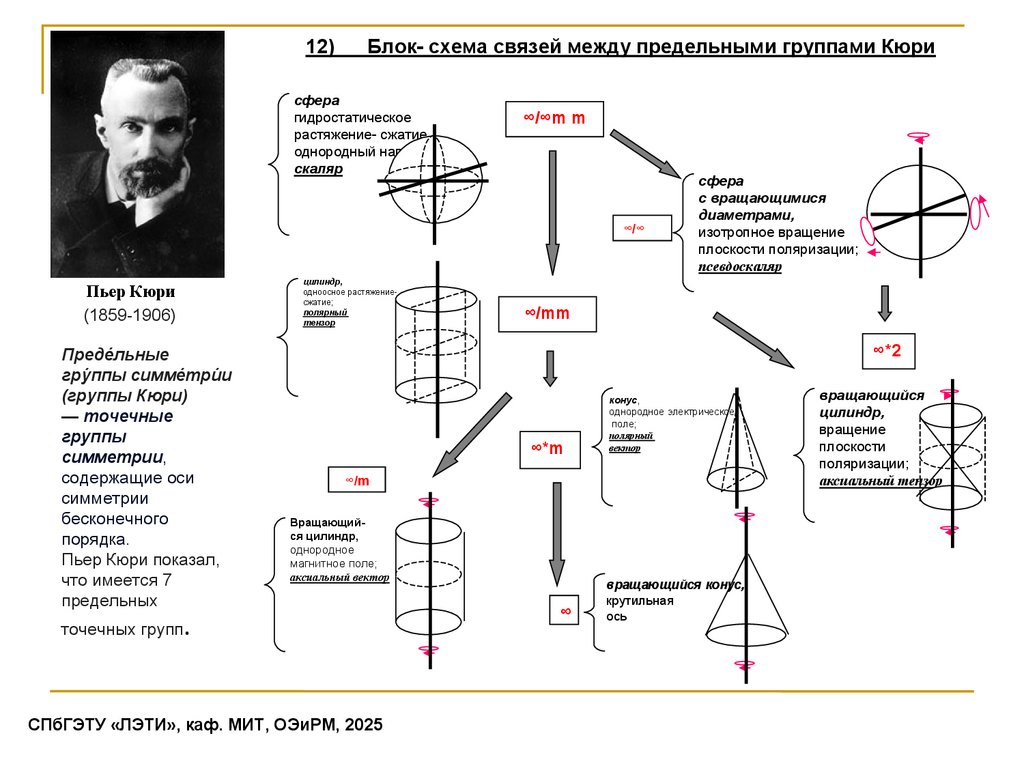
Принцип суперпозиции Кюри (1894г)
Если несколько явлений природы накладываются друг на друга,
образуя единую систему, то в результирующем явлении останутся только те
элементы симметрии, которые являются общими для складываемых
явлений в отдельности.
-Согласно принципу Кюри кристалл под внешним воздействием изменяет свою
точечную симметрию так, что складывается дисимметрия, т.е. кристалл сохраняет
лишь элементы симметрии, общие с элементами симметрии воздействия.
Принцип Неймана связывает симметрию свойств кристалла с симметрией кристалла до
воздействия, в то время как принцип суперпозиции Кюри позволяет определить
симметрию кристалла после воздействия.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

5.

Физические воздействия на кристаллы имеют следующие
группы симметрии:
*электрическое поле, поляризация и другие свойства, описываемые полярным вектором ∞m;
* магнитное поле, намагниченность и другие свойства, описываемые аксиальным вектором
- ∞/m;
* всестороннее сжатие или растяжение кристалла (кристалл растягивается во всех
направлениях с одинаковой силой) - ∞∞m;
* одноосное сжатие или растяжение (кристалл растягивается вдоль одной из осей) - ∞/m mm;
воздействия(кристалл
описывается
предельными
классами симметрии
Кюри
*Симметрия
сдвиговое воздействие
подвергается
скалывающему
воздействию)
- mmm.
Они получаются путем предельного перехода: увеличением
порядка оси симметрии от конечного значения до бесконечного. Таким образом, предельные
группы обязательно содержат оси симметрии бесконечного порядка - ∞
Пример: Определить симметрию флажка, получаемого
вырезанием треугольника из квадратной заготовки.
1. Симметрия квадрата - L44P (4m)
2. Симметрия воздействия, вырезание треугольникаL33P (3m)
3. Найдем результат сложением диссиметрии:
общим элементом симметрии будет одна бщая плоскость
Р (m)
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

6.

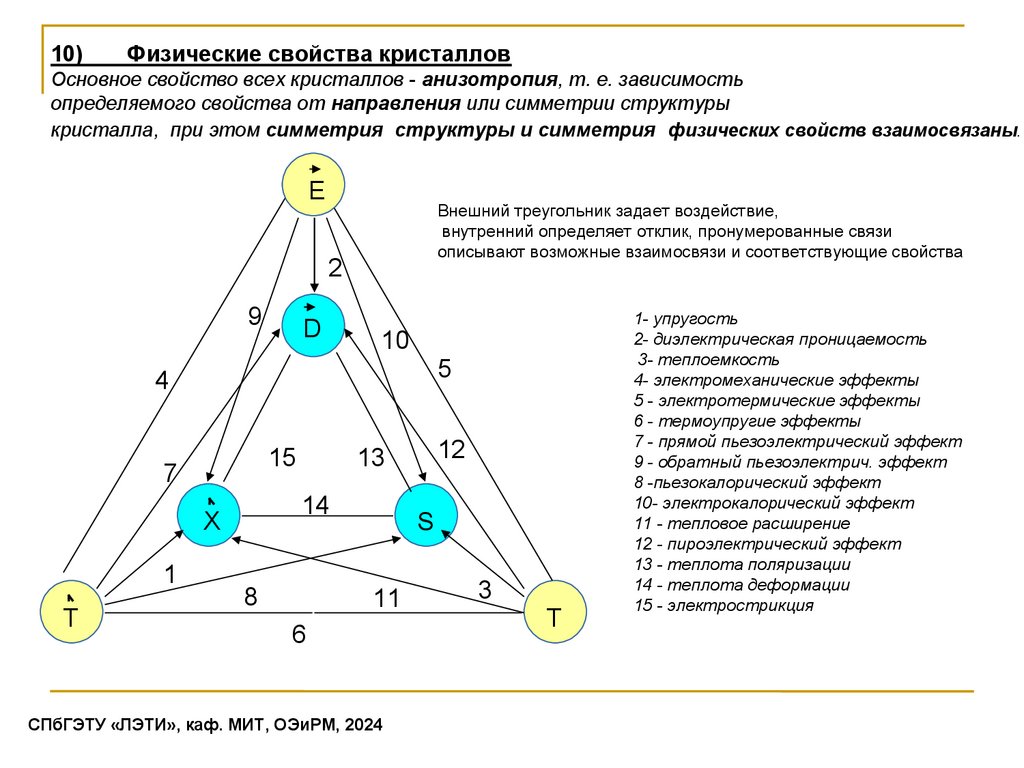
12)
Блок- схема связей между предельными группами Кюри
сфера
гидростатическое
растяжение- сжатие,
однородный нагрев;
скаляр
∞/∞m m
∞/∞
Пьер Кюри
(1859-1906)
Преде́ льные
гру́ ппы симме́ три́ и
(группы Кюри)
— точечные
группы
симметрии,
содержащие оси
симметрии
бесконечного
порядка.
Пьер Кюри показал,
что имеется 7
предельных
цилиндр,
одноосное растяжениесжатие;
полярный
тензор
сфера
с вращающимися
диаметрами,
изотропное вращение
плоскости поляризации;
псевдоскаляр
∞/mm
∞*2
∞*m
конус,
однородное электрическое
поле;
полярный
вектор
∞/m
Вращающийся цилиндр,
однородное
магнитное поле;
аксиальный вектор
точечных групп.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
∞
вращающийся конус,
крутильная
ось
вращающийся
цилиндр,
вращение
плоскости
поляризации;
аксиальный тензор

7.

Принцип суперпозиции Кюри
явление (эффект) = свойство x воздействие
Одноосное растяжениесжатие приложено вдоль
разных осей симметрии куба
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024
+
∞
mm
=?

8.

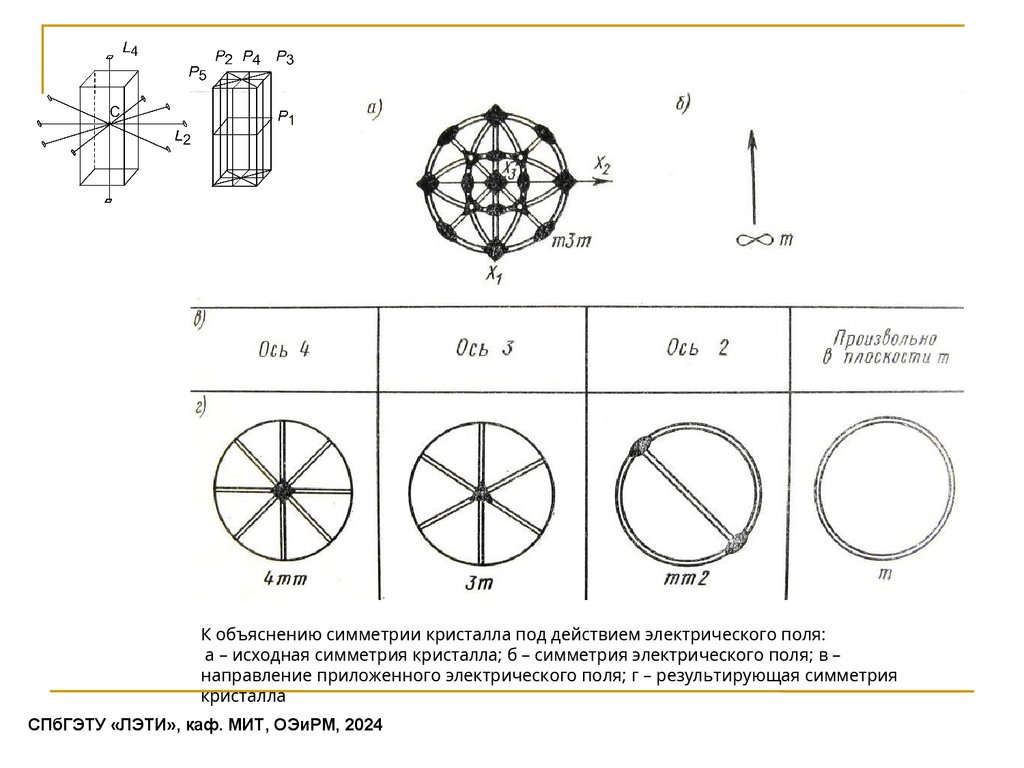
К объяснению симметрии кристалла под действием электрического поля:
а – исходная симметрия кристалла; б – симметрия электрического поля; в –
направление приложенного электрического поля; г – результирующая симметрия
кристалла
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024

9.

Симметрия физических свойств и симметрия структуры кристаллов
Диэлектрическая проницаемость
+
E
-
D1=ε11 E1+ ε12 E2 + ε13 E3
D2=ε21 E1+ ε22 E2 + ε23 E3
D
D3=ε31 E1+ ε32 E2 + ε33 E3
ε11 ε12 ε13
ε =εij = ε21 ε22 ε23
(1)
(2);
D = ε E (1a)
ε -Тензор 2-го ранга
Dj=εij Ei, (1b)
εij =εji
где: ij =1,2,3
ε31 ε32 ε33
Симметрия тензора
(число независимых компонент)
определяется
симметрией структуры кристалла
Число компонент тензора n-го ранга:
N= 3n
n=o, N=1 - скаляр, изотропная среда; симметрия сферы в покое
n=1, N=3 – полярный вектор, анизотропная среда, симметрия конуса в покое и
аксиальный вектор, симметрия вращающегося цилиндра;
n=2, N=9 – тензор 2-го ранга, анизотропная среда, симметрия цилиндра;
n=3, N=27- тензор 3-го ранга;
n=4, N=81- тензор 4-го ранга.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024
Вольдемар Фойгт
(1850—1919)

10.

Тензоры, описывающие физические свойства кристаллов
1) Тензор нулевого ранга (скаляр)
плотность, сжимаемость, теплоемкость
2)Тензор первого ранга (вектор)
пироэлектрический коэффициент, теплота поляризации, электрокалорический коэффициент,
электрическая поляризация при гидростатическом сжатии
3) Тензор второго ранга (связывающий два вектора)
диэлектрические проницаемость, непроницаемость, восприимчивость, магнитные проницаемость и
восприимчивость, удельные сопротивление и электропроводность, коэффициент теплопроводности,
тепловое сопротивление, термоэлектрические коэффициенты
Вектор = (Тензор 2-го ранга)*( вектор)
Dj=εij Ei
4) Тензор второго ранга (связывающий скаляр и тензор второго ранга)
деформация при гидростатическом сжатии, тепловое расширение, термическое напряжение,
термоэлектрические коэффициенты Пельтье
5) Тензор третьего ранга (связывающий вектор и тензор второго ранга)
модуль прямого пьезоэлектрического эффекта, модуль обратного пьезоэлектрического эффекта,
коэффициент электрооптического эффекта (линейного), коэффициент Холла
Pi = dijkTjk
Вектор = (тензор 3-го ранга) * (тензор 2-го ранга)
6) Тензор четвертого ранга (связывающий два тензора второго ранга)
коэффициент магнитострикции, пьезоэлектрический коэффициент, пьезорезистивный коэффициент,
коэффициенты упругости, электрооптический эффект (квадратичный), электрострикция
Тензор 2-го ранга = (тензор 4-го ранга) *( тензор 2-го ранга)
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
Xij=Sijkl Tkl

11.

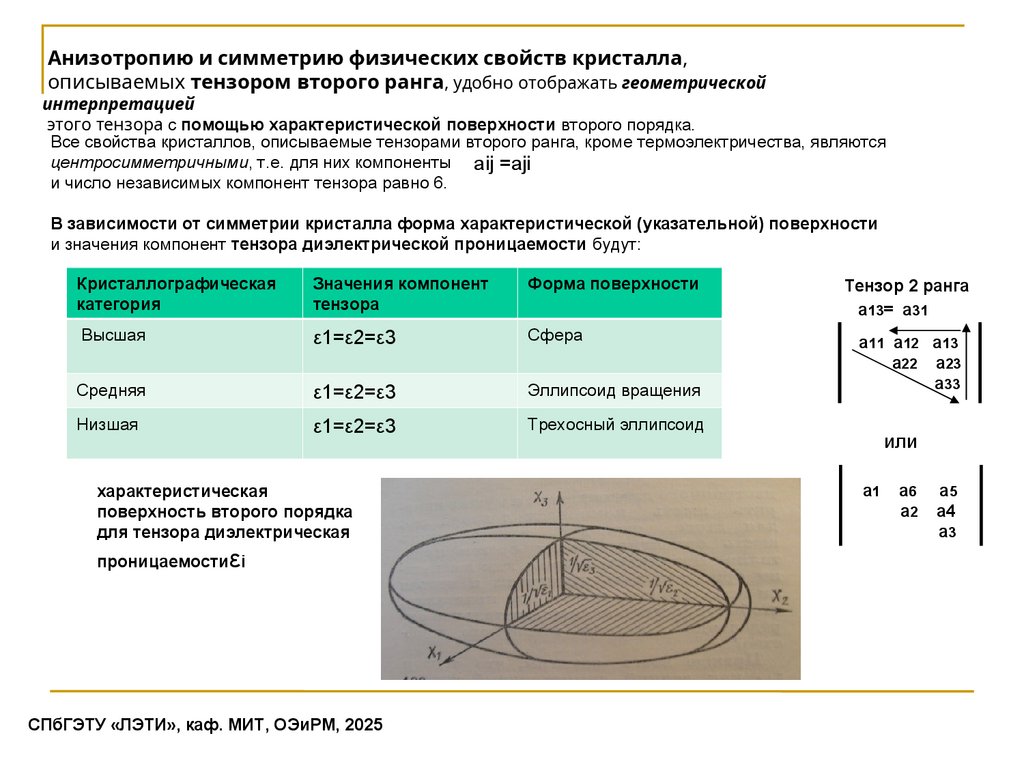
Анизотропию и симметрию физических свойств кристалла,
описываемых тензором второго ранга, удобно отображать геометрической
интерпретацией
этого тензора с помощью характеристической поверхности второго порядка.
Все свойства кристаллов, описываемые тензорами второго ранга, кроме термоэлектричества, являются
центросимметричными, т.е. для них компоненты aij =aji
и число независимых компонент тензора равно 6.
В зависимости от симметрии кристалла форма характеристической (указательной) поверхности
и значения компонент тензора диэлектрической проницаемости будут:
Кристаллографическая
категория
Значения компонент
тензора
Форма поверхности
Высшая
ε1=ε2=ε3
Сфера
Средняя
ε1=ε2=ε3
Эллипсоид вращения
Низшая
ε1=ε2=ε3
Трехосный эллипсоид
характеристическая
поверхность второго порядка
для тензора диэлектрическая
проницаемостиεi
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
Тензор 2 ранга
а13= а31
а11 а12 а13
а22 а23
а33
или
а1
а6
а2
а5
а4
а3

12.

Ось C
Z-срез
Пример 1: Кристалл сапфира
Z [0001]
57.6 o
nr
Сингония: тригональная, класс симметрии с3m
)Диэлектрическая проницаемость сапфира различна в направлении
m-срез
r-срез главной кристаллографической оси [0001] и перпендикулярно к ней и в
прямоугольной системе координат, описывается диагональным тензором второго
ранга:
X[1120]
Y[1100]
ε xx 0 0
ε r 0 ε yy 0
0 0 ε zz
ε xx ε yy ε
ε zz ε||
ε 9,4 ε|| 11,6
Переход от тензора диэлектрической проницаемости в главных осях к тензору для произвольного среза
монокристалла сапфира сводится к переводу исходного тензора в новую систему координат, развернутую
на угол θ относительно оси c, и описывается матричным преобразованием вида
ε r U ε r U 1
ε - исходный тензор в главных осях; ε r – -тензор среза (в новых осях);
U – оператор поворота, определяющий взаимное соответствие между исходной и новой системами координат
r
Для r-среза и m-среза оператор поворота соответственно имеет вид:
0 1
0
0
1 0
U
sin
θ
cos
θ
0
U r 0 cos θr sin θr
m
m
m
cos
θ
sin
θ
0
m
m
0 sin θr cos θ r
,
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
– тензор среза (в новых осях);
здесь : θ r 57.6
θ m 90

13.

Пример 2:
Параметры распространения электромагнитной волны в планарных ЛП на подложке из
сапфира зависят от ориентации полосковых проводников на поверхности подложки. Для
микрополосковой линии (МПЛ), произвольно ориентированной на сапфировой подложке
(рисунок 1.4), расчет компонентов тензора диэлектрической проницаемости r- и m-срезов в
зависимости от угла φ
между направлением распространения электромагнитной волны и проекцией оси с
на поверхность подложки осуществляется при помощи матричного преобразования,
с использованием оператора поворота
cos φ sin φ 0
Z', Z''
57.6°
X''
V r ,m sin φ cos φ 0
0
0 1
Ось C
Y'
Y''
X'
Микрополосковая линия на
подложке из сапфира r-среза
Таблица
Компоненты тензора диэлектрической
проницаемости сапфира r-среза
в зависимости от угла поворота
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
В качестве исходного тензора в таком матричном
преобразовании используется тензор диэлектрической
проницаемости конкретного среза, который рассчитывается
по формулам для r-среза и m-среза
1
r
r
ε U ε U
φ (град.)
εXX
εYY
εZZ
εXY
εXZ
εYZ
0
9,40
10,97
10,03
0
0
-0,99
22,5
9,63
10,74
10,03
0,55
-0,38
-0,92
45,0
10,18
10,18
10,03
0,78
-0,70
-0,70
67,5
10,74
9,63
10,03
0,55
-0,92
-0,38
90,0
10,97
9,40
10,03
0
-0,99
0
112,5
10,74
9,63
10,03
-0,55
-0,92
0,38
Синий цвет сапфира обусловлен примесями титана и
135,0
10,18
10,18
10,03
-0,78
-0,70
0,70
железа в матрице Al2O3. Примесь хрома даёт розовый окрас,
157,5
9,63
10,74
10,03
-0,55
-0,38
0,92
такие корунды называют рубинами.
180,0
9,40
10,97
10,03
0
0
0,99

14.

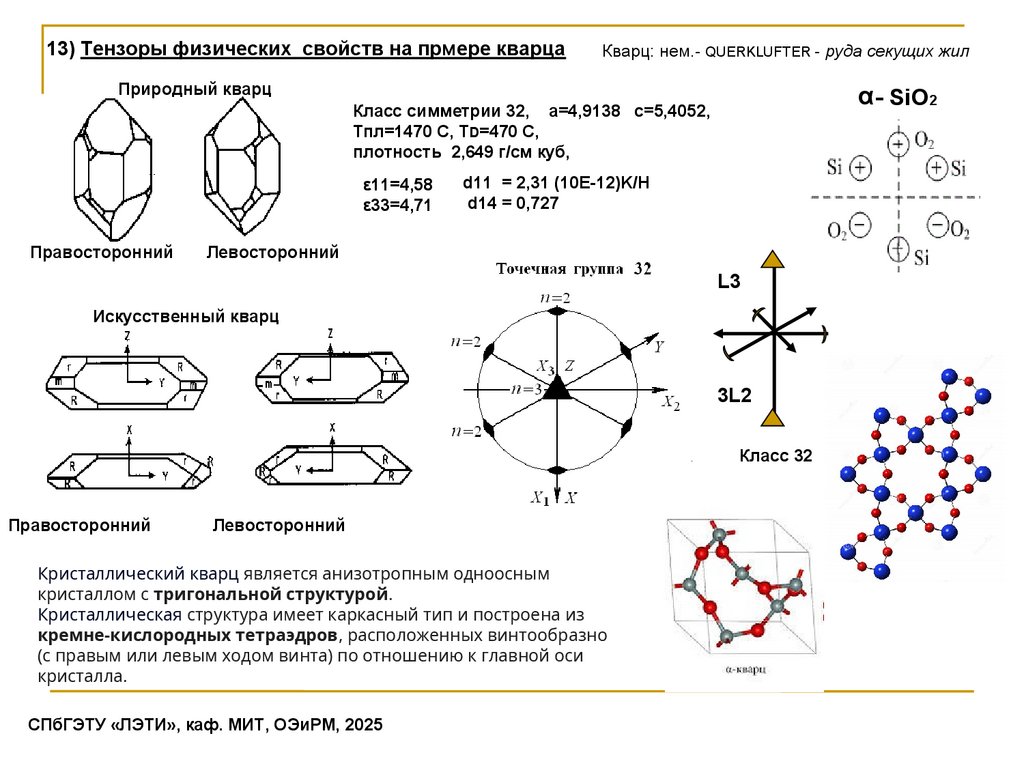
13) Тензоры физических свойств на прмере кварца
Кварц: нем.- QUERKLUFTER - руда секущих жил
Природный кварц
α- SiO2
Класс симметрии 32, а=4,9138 с=5,4052,
Тпл=1470 С, ТD=470 C,
плотность 2,649 г/см куб,
ε11=4,58
ε33=4,71
Правосторонний
d11 = 2,31 (10E-12)K/Н
d14 = 0,727
Левосторонний
L3
Искусственный кварц
3L2
Класс 32
Правосторонний
Левосторонний
Кристаллический кварц является анизотропным одноосным
кристаллом с тригональной структурой.
Кристаллическая структура имеет каркасный тип и построена из
кремне-кислородных тетраэдров, расположенных винтообразно
(с правым или левым ходом винта) по отношению к главной оси
кристалла.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

15.

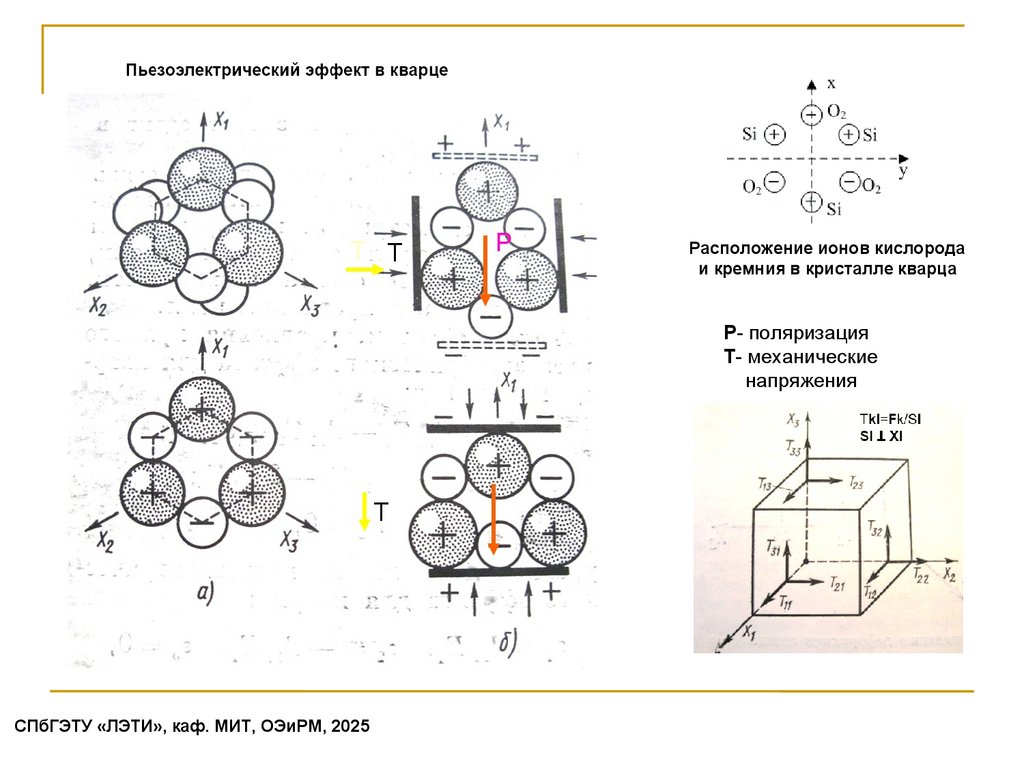
Т
Расположение ионов кислорода
и кремния в кристалле кварца
Р- поляризация
Т- механические
напряжения
Т
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

16.

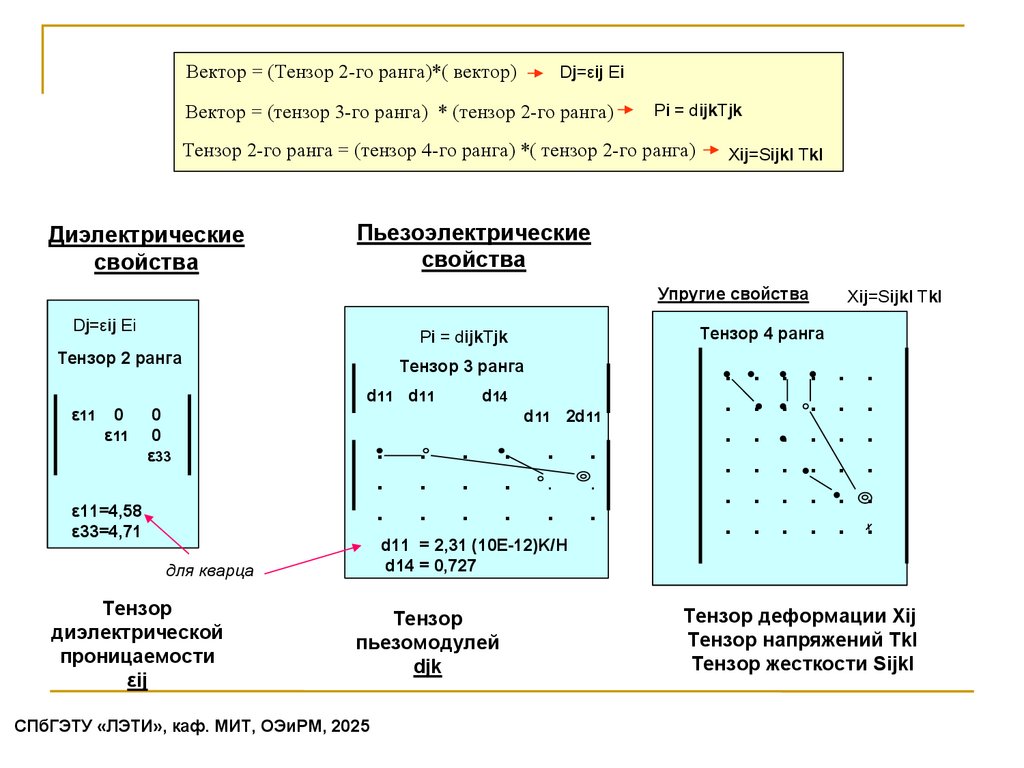
Вектор = (Тензор 2-го ранга)*( вектор)
Dj=εij Ei
Вектор = (тензор 3-го ранга) * (тензор 2-го ранга)
Pi = dijkTjk
Тензор 2-го ранга = (тензор 4-го ранга) *( тензор 2-го ранга)
Диэлектрические
свойства
Xij=Sijkl Tkl
Пьезоэлектрические
свойства
Упругие свойства
Dj=εij Ei
Тензор 3 ранга
d11 d11
ε11
0
ε11
Тензор 4 ранга
Pi = dijkTjk
Тензор 2 ранга
0
0
ε33
ε11=4,58
ε33=4,71
.
.
.
.
.
.
.
.
.
.
.
.
d11 = 2,31 (10E-12)K/Н
d14 = 0,727
для кварца
Тензор
диэлектрической
проницаемости
εij
d14
d11 2d11
.
.
.
Тензор
пьезомодулей
djk
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
Xij=Sijkl Tkl
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Тензор деформации Xij
Тензор напряжений Tkl
Тензор жесткости Sijkl

17.

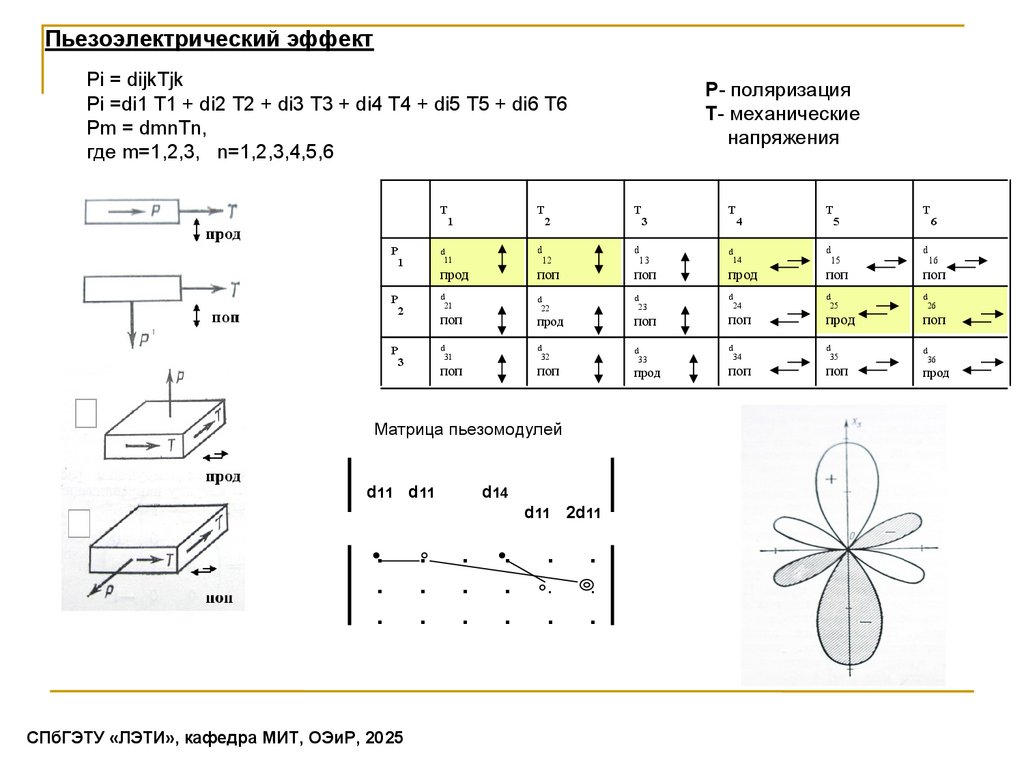
Пьезоэлектрический эффект
Pi = dijkTjk
Pi =di1 T1 + di2 T2 + di3 T3 + di4 T4 + di5 T5 + di6 T6
Pm = dmnTn,
где m=1,2,3, n=1,2,3,4,5,6
Т
Т
1
Р- поляризация
Т- механические
напряжения
Т
2
3
Т
4
Т
5
Т
6
Р
1
d
11
d
12
d
13
d
14
d
15
d
16
прод
поп
поп
прод
поп
поп
Р
2
d
21
d
d
d
d
поп
Р
3
23
24
d
25
прод
поп
поп
прод
поп
d
31
d
d
d
34
d
35
d
поп
поп
поп
поп
прод
22
32
прод
Матрица пьезомодулей
d11 d11
d14
d11 2d11
.
.
.
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2025
.
.
.
.
.
.
.
.
.
.
.
.
33
.
.
.
26
36

18.

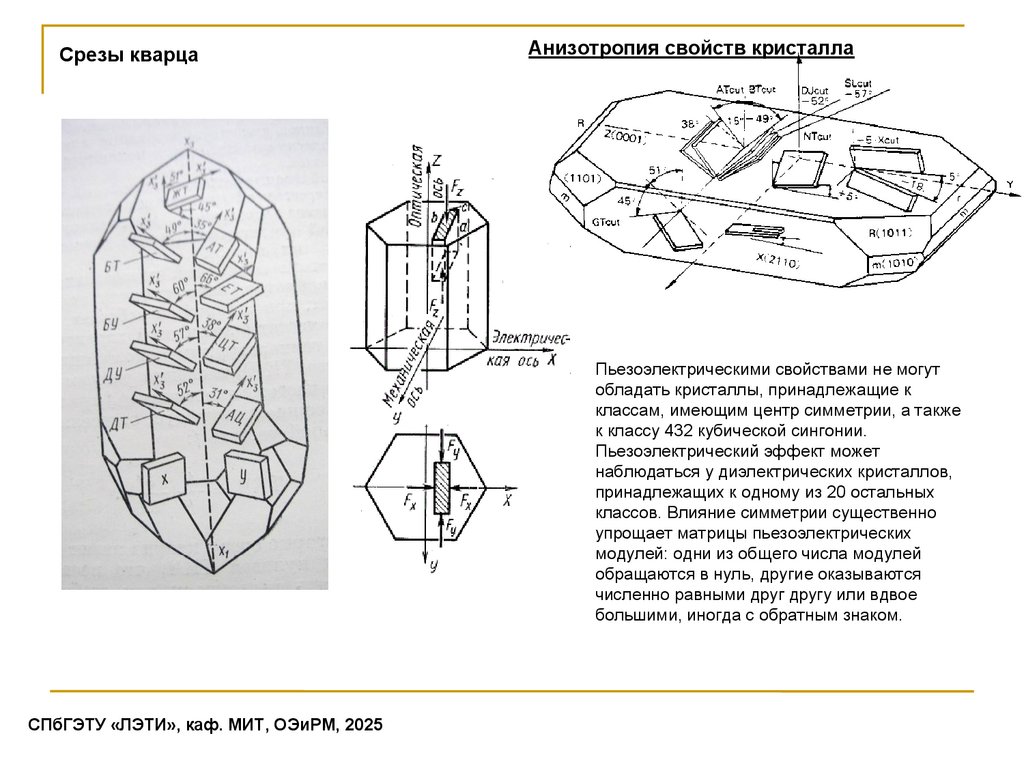
Срезы кварца
Анизотропия свойств кристалла
Пьезоэлектрическими свойствами не могут
обладать кристаллы, принадлежащие к
классам, имеющим центр симметрии, а также
к классу 432 кубической сингонии.
Пьезоэлектрический эффект может
наблюдаться у диэлектрических кристаллов,
принадлежащих к одному из 20 остальных
классов. Влияние симметрии существенно
упрощает матрицы пьезоэлектрических
модулей: одни из общего числа модулей
обращаются в нуль, другие оказываются
численно равными друг другу или вдвое
большими, иногда с обратным знаком.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

19.

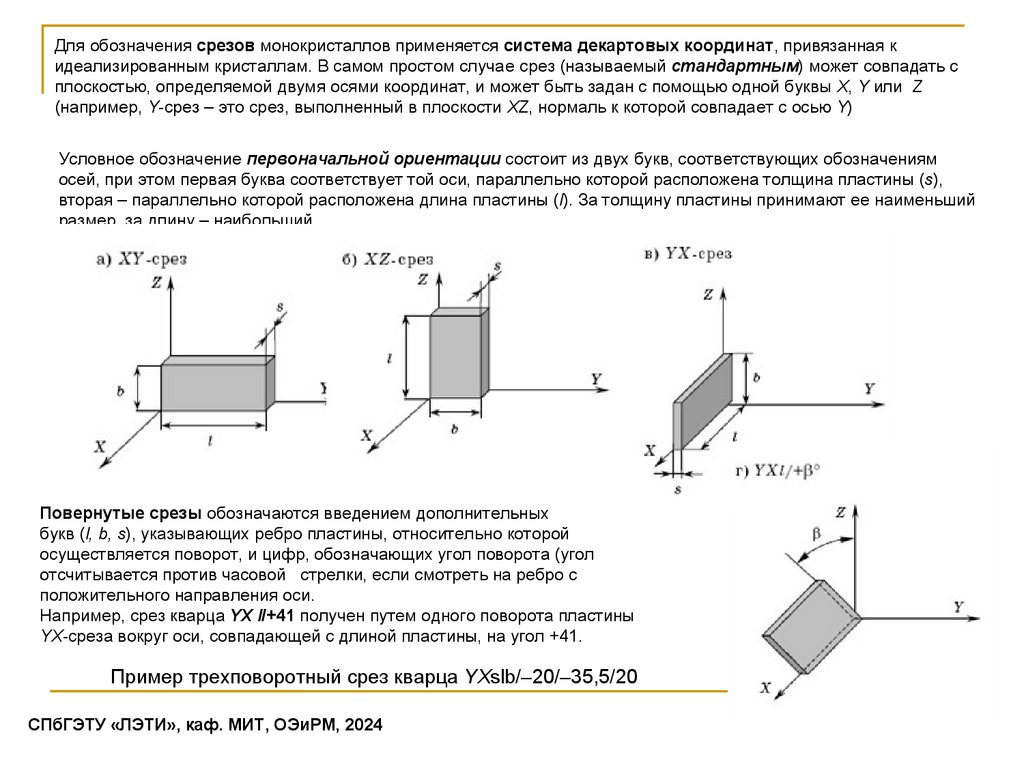
Для обозначения срезов монокристаллов применяется система декартовых координат, привязанная к
идеализированным кристаллам. В самом простом случае срез (называемый стандартным) может совпадать с
плоскостью, определяемой двумя осями координат, и может быть задан с помощью одной буквы X, Y или Z
(например, Y-срез – это срез, выполненный в плоскости XZ, нормаль к которой совпадает с осью Y)
Условное обозначение первоначальной ориентации состоит из двух букв, соответствующих обозначениям
осей, при этом первая буква соответствует той оси, параллельно которой расположена толщина пластины (s),
вторая – параллельно которой расположена длина пластины (l). За толщину пластины принимают ее наименьший
размер, за длину – наибольший.
Повернутые срезы обозначаются введением дополнительных
букв (l, b, s), указывающих ребро пластины, относительно которой
осуществляется поворот, и цифр, обозначающих угол поворота (угол
отсчитывается против часовой стрелки, если смотреть на ребро с
положительного направления оси.
Например, срез кварца YX l/+41 получен путем одного поворота пластины
YX-среза вокруг оси, совпадающей с длиной пластины, на угол +41.
Пример трехповоротный срез кварца YXslb/–20/–35,5/20
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024

20.

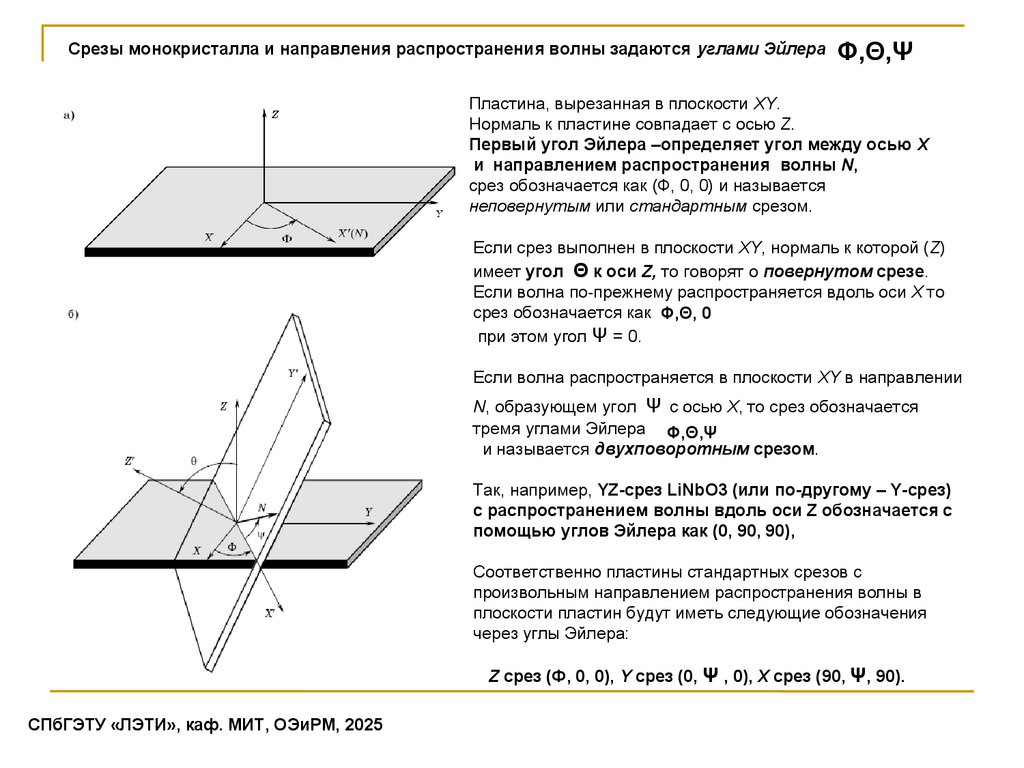
Cрезы монокристалла и направления распространения волны задаются углами Эйлера Φ,Θ,Ψ
Пластина, вырезанная в плоскости XY.
Нормаль к пластине совпадает с осью Z.
Первый угол Эйлера –определяет угол между осью X
и направлением распространения волны N,
срез обозначается как (Ф, 0, 0) и называется
неповернутым или стандартным срезом.
Если срез выполнен в плоскости XY, нормаль к которой (Z)
имеет угол Θ к оси Z, то говорят о повернутом срезе.
Если волна по-прежнему распространяется вдоль оси X то
срез обозначается как Φ,Θ, 0
при этом угол Ψ = 0.
Если волна распространяется в плоскости XY в направлении
N, образующем угол Ψ с осью X, то срез обозначается
тремя углами Эйлера Φ,Θ,Ψ
и называется двухповоротным срезом.
Так, например, YZ-срез LiNbO3 (или по-другому – Y-срез)
с распространением волны вдоль оси Z обозначается с
помощью углов Эйлера как (0, 90, 90),
Соответственно пластины стандартных срезов с
произвольным направлением распространения волны в
плоскости пластин будут иметь следующие обозначения
через углы Эйлера:
Z срез (Ф, 0, 0), Y срез (0, Ψ , 0), X срез (90, Ψ, 90).
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

21.

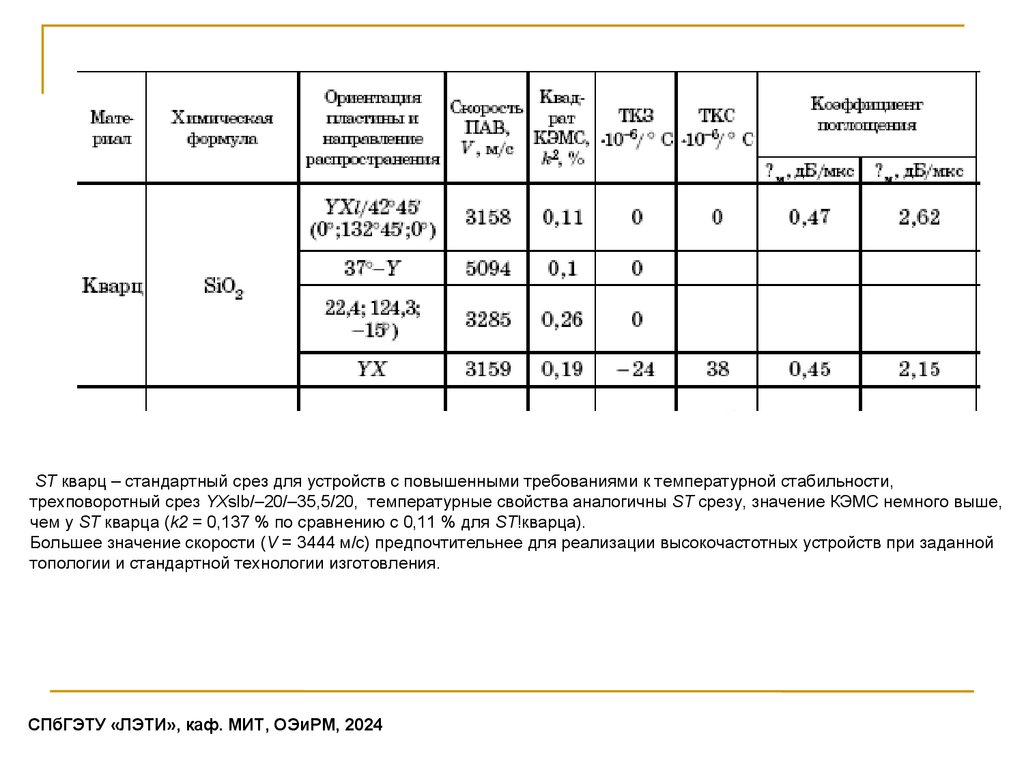
ST кварц – стандартный срез для устройств с повышенными требованиями к температурной стабильности,
трехповоротный срез YXslb/–20/–35,5/20, температурные свойства аналогичны ST срезу, значение КЭМС немного выше,
чем у ST кварца (k2 = 0,137 % по сравнению с 0,11 % для ST!кварца).
Большее значение скорости (V = 3444 м/с) предпочтительнее для реализации высокочастотных устройств при заданной
топологии и стандартной технологии изготовления.
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024

22.

Пример использования прямого и обратного пьезо-эффектов для преобразования радиосигнала
Для количественного описания пьезоэлектрического эффекта используется коэффициент
электромеханической связи (КЭМС), определяющий соотношение между электрической и
механической энергиями в пьезоэлектрике
k2=W12/ W1 W2
Где: W1 , W2 ,W12 – соответственно энергия механических колебаний (механическая энергия),
энергия электрических колебаний (электрическая энергия) и энергия взаимодействия
механических и электрических колебаний (пьезоэлектрическая энергии).
Большее значение скорости (V = 3444 м/с) предпочтительнее для реализации
высокочастотных устройств при заданной топологии
и стандартной технологии изготовления.
Поверхностные акустические волны ПАВ– это упругие возмущения атомов, распространяющиеся в тонком приповерхностном слое
твердого тела.
В акустоэлектронных устройствах поверхностная волна распространяется по поверхности звукопровода из пьезоэлектрика.
- ПАВ имеют невысокую скорость распространения (Vп =1000...4000 м/с, что на пять порядков меньше скорости света);
- Распространение ПАВ происходит без дисперсии и затухания до частот 1…1,5 ГГц;
- При распространении в кристаллах характеристики ПАВ зависят от направления распространения относительно кристаллографических
осей;
T = L/Vп,
Многоотводные линии задержки на пав
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2024

23.

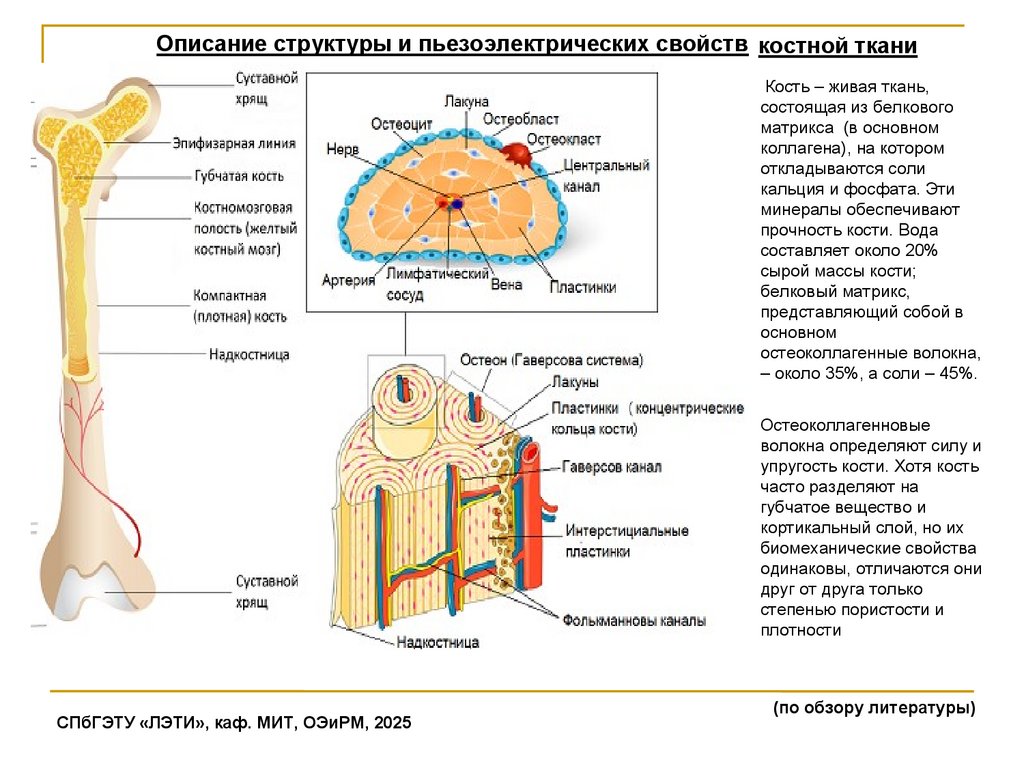
Описание структуры и пьезоэлектрических свойств костной ткани
Кость – живая ткань,
состоящая из белкового
матрикса (в основном
коллагена), на котором
откладываются соли
кальция и фосфата. Эти
минералы обеспечивают
прочность кости. Вода
составляет около 20%
сырой массы кости;
белковый матрикс,
представляющий собой в
основном
остеоколлагенные волокна,
– около 35%, а соли – 45%.
Остеоколлагенновые
волокна определяют силу и
упругость кости. Хотя кость
часто разделяют на
губчатое вещество и
кортикальный слой, но их
биомеханические свойства
одинаковы, отличаются они
друг от друга только
степенью пористости и
плотности
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025
(по обзору литературы)

24.

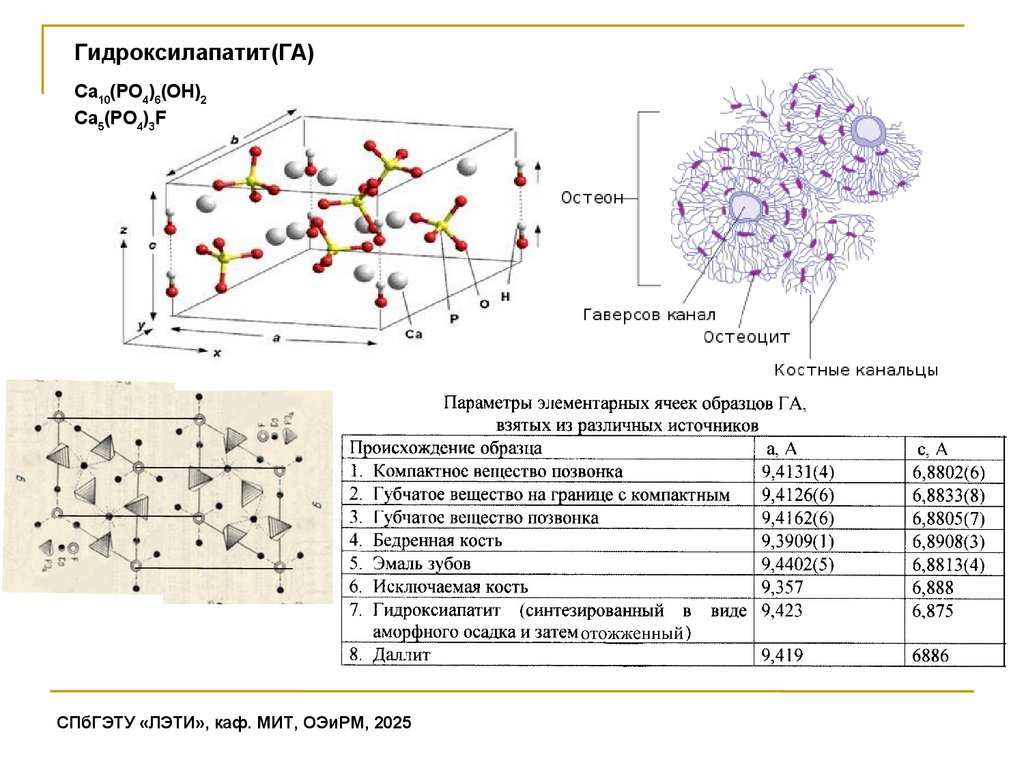
Гидроксилапатит(ГА)
Са10(РО4)6(ОН)2
Са5(РО4)3F
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025

25.

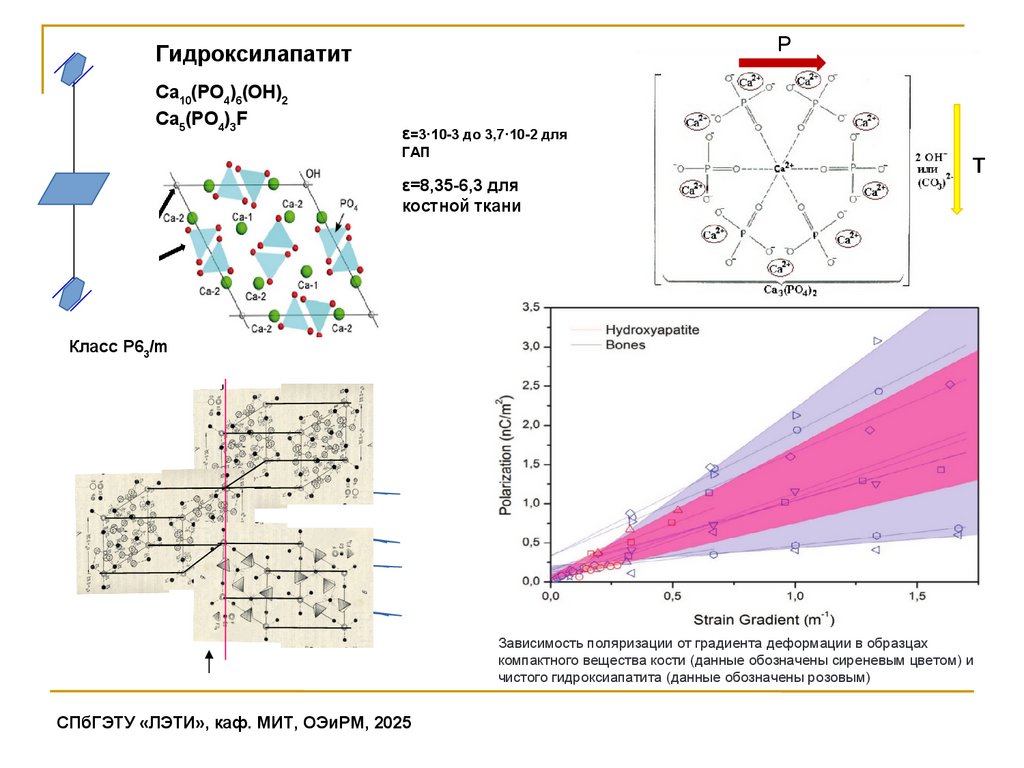
P
Гидроксилапатит
Са10(РО4)6(ОН)2
Са5(РО4)3F
ε=3·10-3 до 3,7·10-2 для
ГАП
т
ε=8,35-6,3 для
костной ткани
Класс P63/m
P
т
Зависимость поляризации от градиента деформации в образцах
компактного вещества кости (данные обозначены сиреневым цветом) и
чистого гидроксиапатита (данные обозначены розовым)
СПбГЭТУ «ЛЭТИ», каф. МИТ, ОЭиРМ, 2025