Статистические методы распознавания

1.

Лекция №2. Статистические методы
распознавания.
Статистические
методы
распознавания
имеют
преимущество перед другими методами в возможности
одновременного учета признаков различной физической
природы, так как используют безразмерные величины –
вероятность появления тех или иных признаков при
различных видах технического состояния объекта.
Наиболее простым и эффективным статистическим
методом распознавания является метод, основанный на
формуле Байеса. Недостаток этого метода состоит в
необходимости
получения
достаточного
объема
предварительной статистической информации, однако, для
таких массовых видов интенсивно эксплуатируемых
объектов, как вагон, этот метод вполне приемлем.
Если имеется диагноз (состояние объекта) Di и признак kj,
встречающийся при этом диагнозе, то имеем вероятность
совместного появления событий: наличие у объекта
состояния Di и признака kj

2.

P( Di k j ) P( Di ) P(k j / Di ) P k j P Di / k j
(2.1)
где P(Dikj) – вероятность логического произведения событий Di и kj;
P(kj /Di ) – условная вероятность: вероятность события kj при
условии, что произошло событие Di.
P(Di / kj) – условная вероятность: вероятность события Di при
условии, что произошло событие kj.
Нас интересует
из формулы (2.1) имеем формулу Байеса:
P ( Di / k j ) P ( Di )
P k j / Di
P k j
детерминистский метод распознавания является частным случаем
вероятностного метода, когда P(Di / kj)=1.
(2.2)

3.

Рассмотрим пример определения вероятности обнаружения
неисправного подшипника по признаку перегрева его корпуса. Обозначим:
D1 – исправное состояние подшипника;
D2 – неисправное состояние подшипника;
признак k1 – перегрев корпуса буксы в интервале от 30 C и выше.
Нас интересует вероятность того, что в буксовом подшипнике
имеется дефект при условии обнаружения перегрева корпуса буксы
свыше 30 C
Пример: Имеем данные анализа обследования Nij подшипников, первый
индекс относится к диагнозу (1- исправное состояние, 2 – дефект, 0 – все
случаи), второй индекс относится к признаку ( 1 – наличие признака
перегрева, 0 – все случаи).
Обследовано N00=10000 подшипников, у которых предварительно
измерялась температура перегрева корпуса буксы в эксплуатационных
условиях. У N20 = 20 подшипников обнаружены дефекты, из них N21 = 18
подшипников имели перегрев корпуса свыше 30 C. Из всей выборки N01=25
подшипников имели перегрев корпуса свыше 30 C.
По данным обследования определяем:
вероятность наличия дефекта подшипника
N 20
20
P D2
0,002
N 00 10000

4.

вероятность наличия признака перегрева корпуса буксы
N 01
25
P k1
0,0025
N 00 10000
вероятность наличия признака перегрева корпуса буксы у дефектного подшипника
N 21 18
P k1 / D2
0,9
N 20 20
вероятность наличия признака перегрева корпуса буксы у исправных
подшипников
N 01 N 21 25 18
P k1 / D1
0,0007
N 00 N 20
9980
В результате, вероятность обнаружения дефектного
подшипника
.
0,9
P( D2 / k1 ) 0,002
0,72
0,0025

5.

Решающее правило в методе Байеса основано на введении порогового
значения для вероятности диагноза:
P( Di / К * ) Pi
где Pi - заранее выбранный уровень распознавания для диагноза Di.
Обычно принимают
Pi 0,9
Поскольку статистический метод распознавания не дает
возможности однозначного решения, то необходимо
.вводить некоторые
условия оптимальности принятия решения.

6.

МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
В методах статистических решений основным условием решающего правила
принимается минимум риска. Следует различать понятия: диагноз D, как
действительное техническое состояние объекта, и принятое решение Н, которое
может быть как правильным (истинным), так и ошибочным (ложным).
Очевидно, что вероятность распознавания зависит от
правильности выбора значения параметра – перегрев корпуса
подшипника по отношению к температуре окружающей среды.
Обозначим этот выбираемый параметр как искомую величину x.
Задача состоит в выборе диагностического признака k =
xо таким образом,
xо следует принимать решение о дефектации подшипника,
что при x
xо допускать дальнейшую эксплуатацию:
при x xо
x D1;
при x xо x D2.
а при x
(3.1)

7.

Перегрев корпуса неоднозначно характеризует состояние подшипника – у
исправного подшипника перегрев корпуса зависит от переизбытка смазки в
приработочный период, от зазоров, теплоотдачи, загрузки вагона,
скорости и режима движения поезда и других условий.
В то же время подшипник может иметь опасные дефекты, не приводящие
какое-то время к перегреву (ослабление торцевого крепления, трещина
кольца и др.).
В зависимости от этих обстоятельств статистические распределения
плотности вероятности диагностического параметра x для дефектных D2
и исправных D1 подшипников имеют вид, показанный на рис. 3.1.

8.

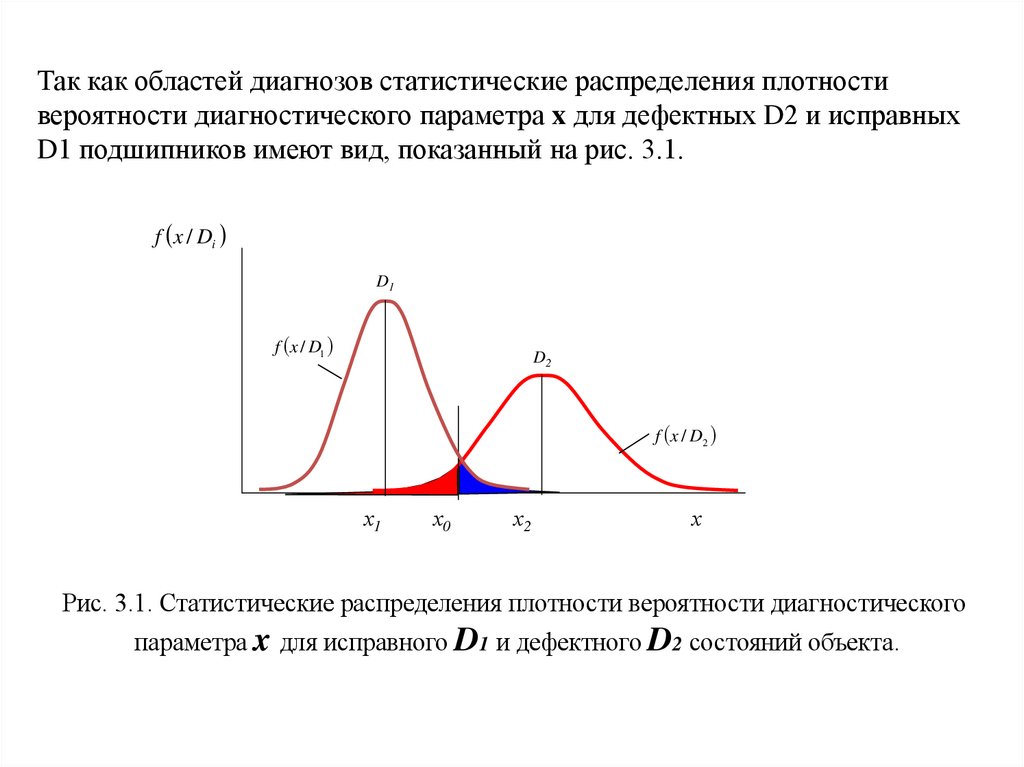
Так как областей диагнозов статистические распределения плотности
вероятности диагностического параметра x для дефектных D2 и исправных
D1 подшипников имеют вид, показанный на рис. 3.1.
f x / Di
D1
f x / D1
D2
f x / D2
х1
х0
х2
х
Рис. 3.1. Статистические распределения плотности вероятности диагностического
параметра x для исправного D1 и дефектного D2 состояний объекта.

9.

Так как области D1 и D2 пересекаются, то, в принципе, невозможно
выбрать значение xо, при котором всегда соблюдалось бы правило (3.1) и не
было ошибочных решений. Поэтому практическая задача состоит в выборе
оптимального xо по каким либо критериям. Рассмотрим сначала возможные
ошибки при принятии решения.
Ложная тревога – случай, когда принимается решение о наличии дефекта,
а в действительности объект находится в исправном состоянии.
Пропуск дефекта – случай принятия решения об исправном состоянии, в то
время когда объект содержит дефект.
Обозначим Hij возможные решения по правилу (3.1) (первый индекс
соответствует принятому решению, второй – действительному состоянию, 1 –
соответствует исправному состоянию, 2 – дефекту), тогда:
Н11 - правильное решение об исправном состоянии;
Н22 – правильное решение о дефектном состоянии;
Н12 – пропуск дефекта;
Н21 – ложная тревога.
Вероятность ложной тревоги Р(Н21), случай, когда при x xо объект
является исправным, но по правилу (3.1) оценивается как дефектный, равна
вероятности произведения двух событий: диагноз D1 и значение x xо при
исправном состоянии.

10.

. Вероятность
x xо при исправном состоянии (условная вероятность
ложной тревоги) определяется площадью, ограниченной кривой плотности
вероятности исправного состояния при x xо
P x xo / D1 f x / D1 .dx ,
(3.2)
xo
тогда вероятность ложной тревоги будет равна произведению
вероятностей диагноза D1 и значения x xо
P H 21 P D1 .P x xo / D1 P1 f x / D1 .dx ,
(3.3)
xo
где Р1=P(D1) – априорная вероятность диагноза D1, принимается на
базе статистических данных.
Аналогично находится вероятность пропуска дефекта:
хо
P H 12 P D2 P x xo / D2 P2 f x / D2 .dx .
(3.4)

11.

Для выбора оптимального xо необходимо дать оценку той и другой
ошибке. После этого можно использовать различные методы выбора, то есть
принятия решения на основе оценки возможного риска.
Для определения среднего риска принимаем цену ложной тревоги С21 и
цену пропуска дефекта С12, тогда средний риск определится выражением
x0
R C21P1 f x / D1 dx C12 P2 f x / D2 dx ,
x0
(3.5)
С21 и С12 – условные значения, оценивающие последствия пропуска дефекта
и ложной тревоги, как правило, принимается С12 С21. В общем случае
вводят цену правильных решений, умножая ее, соответственно, на
вероятности соответствующих правильных решений, при этом цена
правильного решения принимается отрицательной. Выражение (3.5)
представляет собой среднее значение (математическое ожидание) риска
при заданном значении х0. Но для оптимизации решения необходимо
задаться каким-то критерием, и в этом случае наиболее оправдан критерий
минимального риска.

12.

Метод минимального риска: находят условие минимума среднего риска.
Дифференцируя (3.5) по xо и приравнивая производную нулю получают
условие экстремума
dR
C21P1 f x0 / D1 C12 P2 f x0 / D2 0 ,
dx0
(3.6)
в практических задачах сложно дать численную оценку стоимости ошибок,
но проще задаться их соотношением, тогда из формулы (3.6) имеем
f x0 / D1 C12 P2
.
f x0 / D2 C 21 P1
(3.7)
Это условие может определять два значения xо – по минимуму и по
максимуму.
Для того, чтобы получить не только необходимое, но и достаточное
условие
2
d R
0
минимума, вторая производная должна быть больше нуля , dx 2 0

13.

для одномодальных распределений можно ограничиться выбором х0
в пределах
x1 x0 x2
(3.8)
В соответствии с правилом (3.1) по методу наименьшего риска принимается
следующее решение о состоянии объекта, имеющего данное значение параметра x
f x / D1
x D1 , если
;
f x / D2
f x / D1
x D2 , если
,
f x / D2
(3.9)
(3.10)
C12 P2
представляет собой пороговое значение для
C 21P1
отношения правдоподобия – отношение плотностей вероятностей
распределения x при двух состояниях.

14.

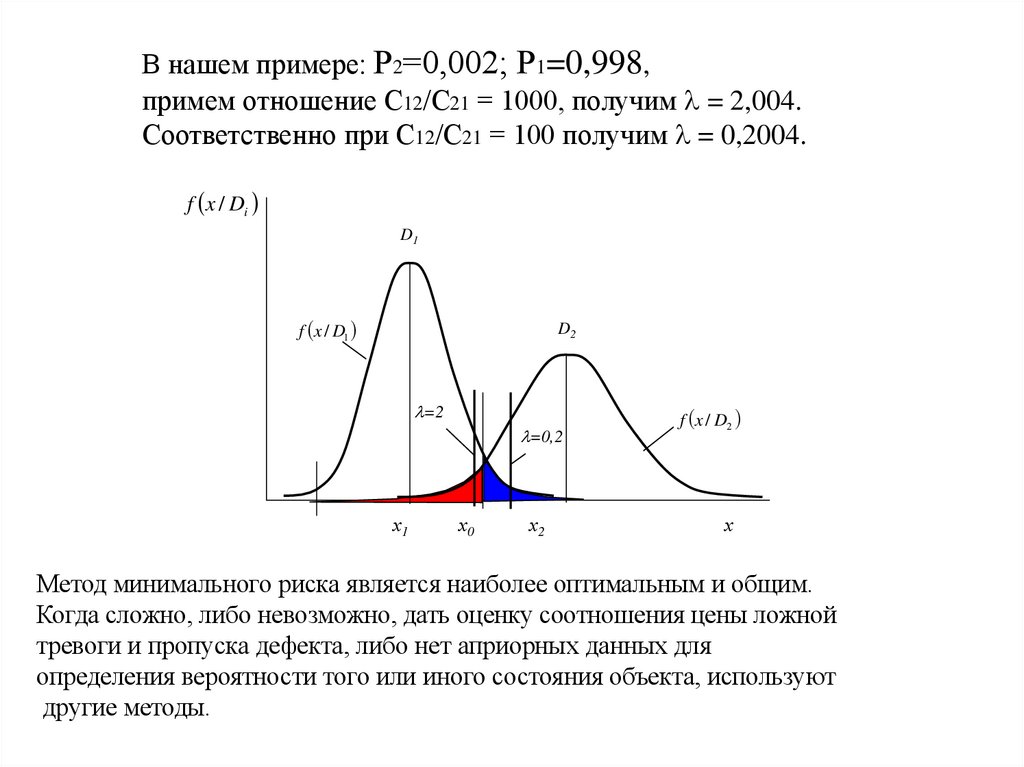
В нашем примере: Р2=0,002; Р1=0,998,
примем отношение С12/С21 = 1000, получим = 2,004.
Соответственно при С12/С21 = 100 получим = 0,2004.
f x / Di
D1
f x / D1
D2
=2
=0,2
х1
х0
х2
f x / D2
х
Метод минимального риска является наиболее оптимальным и общим.
Когда сложно, либо невозможно, дать оценку соотношения цены ложной
тревоги и пропуска дефекта, либо нет априорных данных для
определения вероятности того или иного состояния объекта, используют
другие методы.

15.

Метод минимального числа ошибочных решений позволяет принима
решение без оценки последствий ошибок.
Вероятность ошибочного решения для решающего правила (3.1)
x0
Рош P1 f x / D1 dx P2 f x / D2 dx,
x0
(3.11)
для значений (3.8) получим условие минимума ошибочных решений
.
dРош
P1 f x0 / D1 P2 f x0 / D2 0 ,
dx0
f x0 / D1 P2
или
f x0 / D2 P1 ,
(3.12)
(3.13)
тогда принимаем следующие решения:
f x0 / D1 Р2
;
f x0 / D2 Р1
f x / D1 Р2
x D2 , если
f x / D2 Р1
x D1 , если
(3.14)
(3.15)
Соотношения (3.13) – (3.15) являются частным случаем метода
минимального риска при условии, что С С
12
21

16.

Метод минимакса применим для ситуации, когда отсутствуют
предварительные статистические данные о вероятности диагнозов
D1 и D2. При этом выбирают значение х0 таким образом, чтобы при
наименее благоприятных значениях Р1 («наихудший случай»)
потери, связанные с ошибочными решениями, были бы
минимальными.
Исходя из условия Р2 = (1 - Р1), будем считать, что величина
риска является функцией х0 и Р1,
x0
R( х0 , Р1 ) C21P1 f x / D1 dx C12 (1 P1 ) f x / D2. dx
(3.16)
x0
Минимизируем риск, приравнивая нулю частные производные
R
0;
x 0
В результате получаем
R
0.
Р1
f ( x0 / D1 ) C12 (1 P1 )
,
f ( x0 / D2 )
C 21 P1
(3.18)
x0
C21 f x / D1 dx C12 f x / D2 dx.
x0
(3.17)
(3.19)

17.

Решая уравнения (3.18) и (3.19) определяем х0 соотношением функций
распределения, которые определяют площади условных вероятностей
ошибок на рис. 3.1.
х0
х0
F ( x0 / D1 ) f (x / D1 )dx; F ( x0 / D2 ) f (x / D2 )dx ;
1 F ( x0 / D1 ) С12
, или
F ( x0 / D2 )
С21
(3.20)
С21 1 F ( x0 / D1 ) С12 F ( x0 / D2 ) . (3.21)
Зависимость (3.21) выражает
равенство условных рисков ошибочных решений.

18.

Метод наибольшего правдоподобия дает решение, не требующее
знания точных значений стоимости ошибок и вероятностей состояния
а только качественно отражающее их соотношение.
Тогда правило решения принимается следующим
x D1 , если
f x0 / D1
1
f x0 / D2
f x / D1
x D2 , если
1,
f x / D2
(3.22)
то есть, граничное значение находится в точке пересечения кривых
плотностей вероятностей из условия
f x0 / D1 f x0 / D2
C12 P2
. 1
C 21P1
(3.23)
Условие (3.23) можно использовать, когда заранее известно,
что
С12 С21,
Р1 Р2.

19.

В условиях работы подвижного состава бывает очень сложно дать количественную
оценку последствий пропуска дефекта. В то же время ложная тревога поддается более
точной оценке потерь, связанных в нашем случае с обнаружением ошибки в принятии
решения. Более того, можно определить допустимый уровень частоты появления ложной
тревоги, не влияющий существенно на работу транспорта в целом.
В данном случае полезно использовать метод Неймана-Пирсона, в
соответствии с которым минимизируется вероятность пропуска
цели (дефекта).
Если задан максимально допустимый уровень вероятности ложной
тревоги L, то условием наименьшей вероятности пропуска дефекта
будет:
P1 f x / D1 .dx L.
(3.24)
xo
Условие (3.24) однозначно определяет величину xо для заданного
уровня вероятности ложной тревоги L.
В ряде случаев можно исходить из заданного значения
вероятности пропуска дефекта F и минимизировать вероятность
ложной тревоги:
хо
P2 f x / D2 .dx F .
(3.25)