Решение задач с помощью систем линейных уравнений. Способы решения систем линейных уравнений

1.

26.02.2025
Классная работа.
Решение задач с помощью
систем линейных уравнений.

2.

Способы решения систем линейных
уравнений:
• графический способ;
• способ подстановки;
• способ сложения.

3.

Задача 1. В корзине лежат бананы и яблоки. Известно, что бананов на 5
больше, чем яблок. Сколько бананов и сколько яблок в корзине, если всего в ней
17 фруктов?
Бананы-?, на 5 больше
Яблоки-?
Решение.
Пусть х – количество бананов в корзине, у – количество яблок. Известно, что бананов
на 5 больше, составим 1 уравнение х-у=5. По условию всего 17 фруктов, составим 2
уравнение х+у=17. Составим и решим систему уравнений.
х − у = 5,
ቊ
х + у = 17,
( х + х) + (– у + у) = 5 + 17,
х + х – у + у = 5 + 17,
2х = 22,
х = 11.
11 бананов и 6 яблок в корзине.
Ответ: 11 бананов и 6 яблок.
11 + у = 17,
у = 17 – 11,
у = 6.

4.

Чтобы решить задачу с помощью
системы уравнений, надо:
• выделить две неизвестные величины и обозначить их буквами;
• используя условие задачи, составить систему уравнений;
• решить систему уравнений удобным способом;
• истолковать результат в соответствии с условием задачи.

5.

Задача 2. Первый ученик за 3 тетради и 2 карандаша заплатил
66 рублей. Второй ученик за такие же 2 тетради и 3 карандаша
заплатил 49 рублей. Сколько стоит тетрадь и сколько стоит
карандаш?
Решение.
Пусть х рублей стоит тетрадь, у рублей стоит карандаш.
3х + 2у = 66, ∙3
ቊ
2х + 3у = 49, ∙ (– 2)
9х + 6у = 198,
ቊ
−4х − 6у = −98,
9х – 4х = 198 – 98,
5х = 100,
х = 100 : 5,
х = 20.
3∙20 + 2у = 66,
60 + 2у = 66,
2у = 66 – 60,
2у = 6,
у = 6 : 2,
у = 3.
тетради
карандаши
Всего
Первый
ученик
3х
2у
66
Второй
ученик
2х
3у
49
20 рублей стоит тетрадь, 3 рубля стоит карандаш.

6.

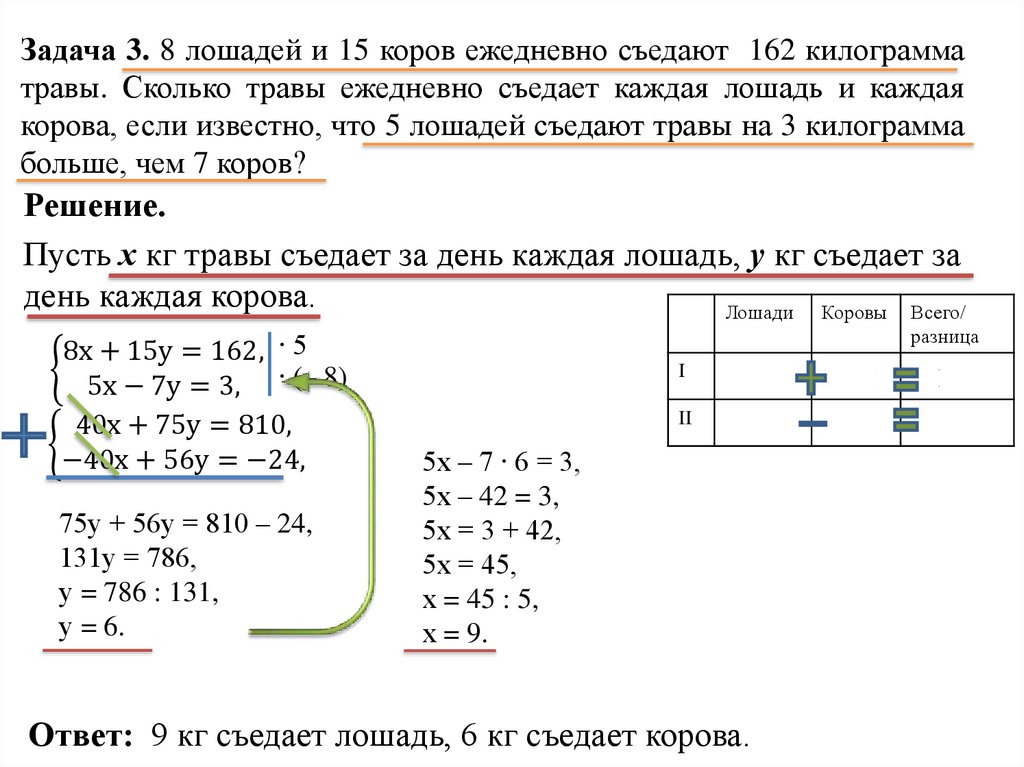
Задача 3. 8 лошадей и 15 коров ежедневно съедают 162 килограмма
травы. Сколько травы ежедневно съедает каждая лошадь и каждая
корова, если известно, что 5 лошадей съедают травы на 3 килограмма
больше, чем 7 коров?
Решение.
Пусть х кг травы съедает за день каждая лошадь, у кг съедает за
день каждая корова.
Лошади Коровы Всего/
8х + 15у = 162, ∙ 5
ቊ
5х − 7у = 3, ∙ (– 8)
40х + 75у = 810,
ቊ
−40х + 56у = −24,
75у + 56у = 810 – 24,
131у = 786,
у = 786 : 131,
у = 6.
разница
I
8х
15у
162
II
5х
7у
3
5х – 7 ∙ 6 = 3,
5х – 42 = 3,
5х = 3 + 42,
5х = 45,
х = 45 : 5,
х = 9.
Ответ: 9 кг съедает лошадь, 6 кг съедает корова.

7.

Закрепление
• №1080. Купец купил 138 аршин черного и
синего сукна за 540 р. Спрашивается, сколько
аршин он купил того и другого, если синее
стоило 5 р. за аршин, а черное 3р.?
• №1082. Чтобы накормить 4 лошадей и 12
коров, надо 120 кг сена в день, а чтобы
накормить 3 лошадей и 20 коров – 167 кг сена.
Найдите дневную норму сена для лошади и
для коровы.

8.

Итог урока
Чтобы решить задачу с помощью
системы уравнений, надо:
• выделить две неизвестные величины и обозначить их буквами;
• используя условие задачи, составить систему уравнений;
• решить систему уравнений удобным способом;
• истолковать результат в соответствии с условием задачи.