Similar presentations:
Начертательная геометрия, инженерная и компьютерная графика
1.
2.
1.2.
3.
4.
Геометрические преобразования.
Виды и определения.
Простейшие преобразования
и их реализация в векторной графике.
Аффинные, проективные и нелинейные
преобразования.
Применение преобразований к решению
практических задач
3.
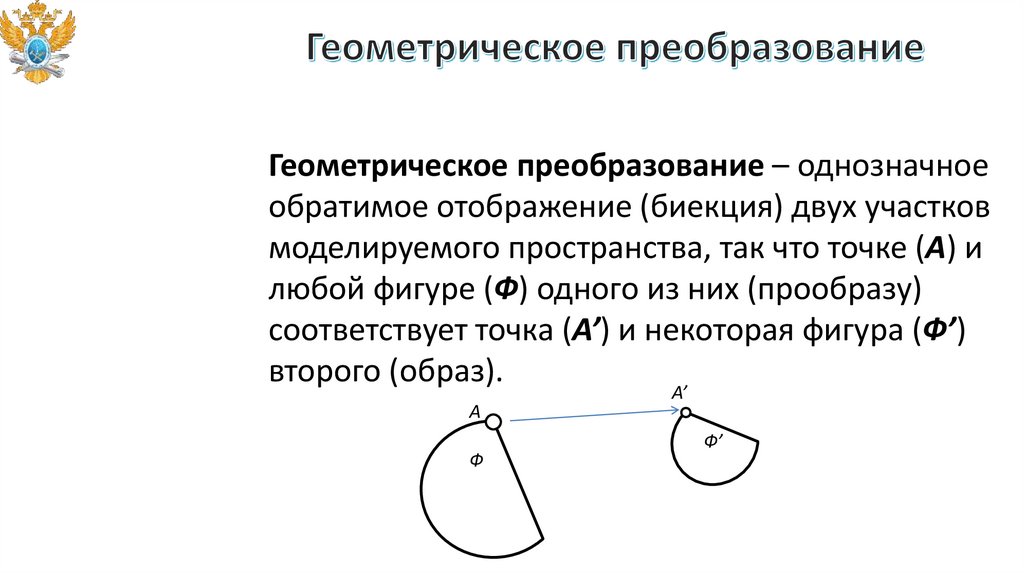
Геометрическое преобразование – однозначноеобратимое отображение (биекция) двух участков
моделируемого пространства, так что точке (A) и
любой фигуре (Ф) одного из них (прообразу)
соответствует точка (A’) и некоторая фигура (Ф’)
второго (образ).
A’
A
Ф
Ф’
4.
• образ f' можно рассматривать как результат движенияили трансформации прообраза f в неизменной
системе координат x–y;
• образ f' можно рассматривать как новое описание
неизменного и неподвижного прообраза f
в измененной системе координат x'–y'.
5.
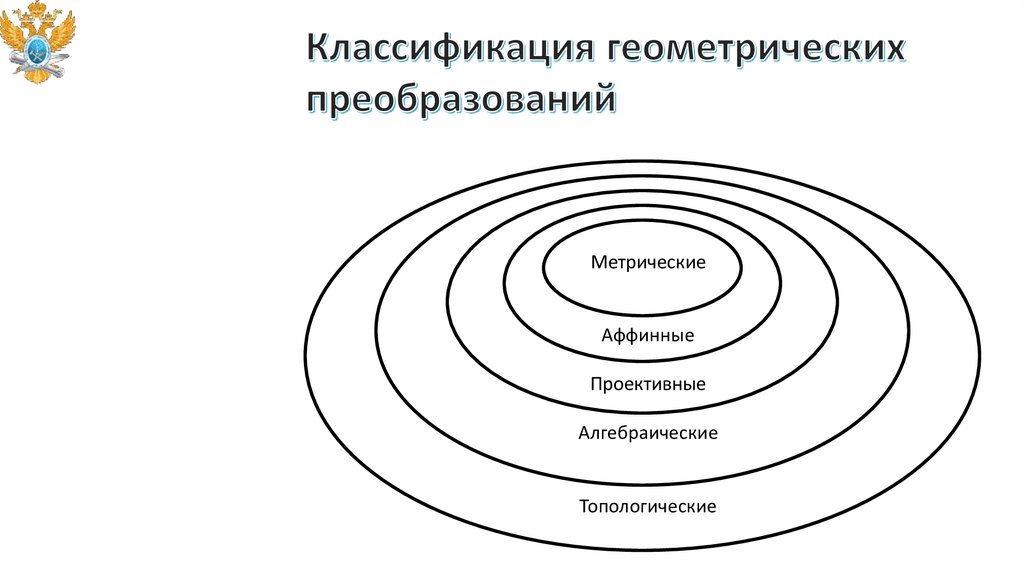
МетрическиеАффинные
Проективные
Алгебраические
Топологические
6.
преобразования движения (сдвиг, поворот, осевая симметрия) и подобия –
инвариантами являются сохранение углов (параллельность,
перпендикулярность и др.), формы фигур с точностью до подобия, порядка
алгебраических кривых, инцидентности (принадлежность фигур) и др.;
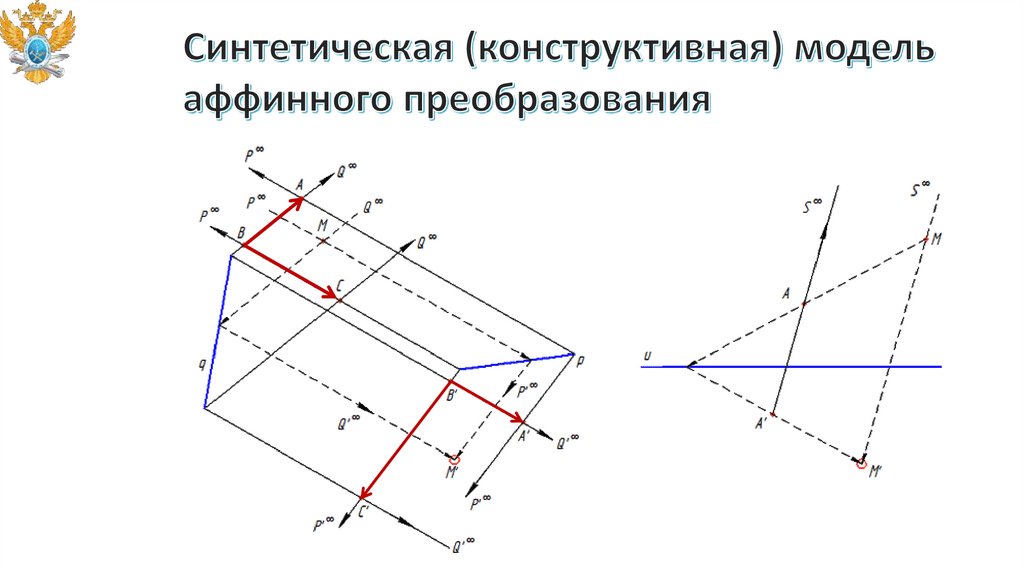
аффинные преобразования не сохраняют постоянными метрические свойства
фигур, в частности, перпендикулярность прямых, форму (окружность может
переходить в эллипс и наоборот), однако другие свойства – параллельность,
инцидентность, порядок алгебраических кривых сохраняются;
проективные преобразования не сохраняют свойства параллельности
прямых, но сохраняют касательность прямых и кривых, инцидентность,
порядок алгебраической кривой (окружность может переходить в параболу
или гиперболу) и т.д.
7.
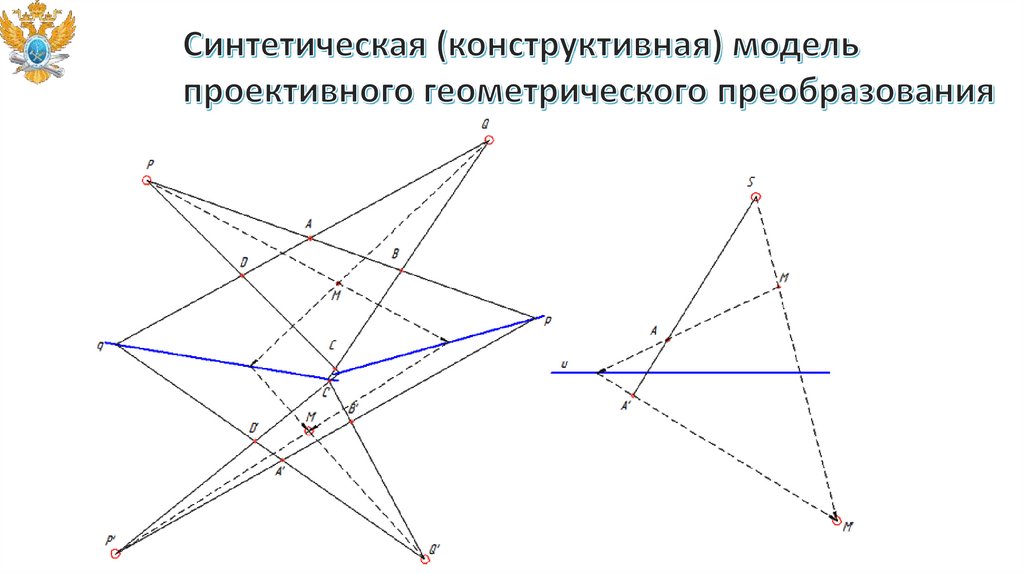
Дано (аппарат преобразования): S, u, A, A’ϵAS.Требуется (задача преобразования):
- Для некоторой точки M найти образ M’.
Построение:
1)
2)
3)
AM пересечь с u;
~ соединить с A’;
~ пересечь с SM.
Геометрическое построение – конструктивный способ
осуществить геометрическое преобразование.
Если геометрические действия привести к вычислению
координат точек и вывести соответствующие формулы,
мы получим аналитическую (вычислительную) модель
геометрического преобразования.
8.
Фотографирование и проецирование.
9.
10.
• Координаты точки (x, y, w) называют однородными.• Перевод однородных координат в декартовы:
xдек = xодн / wодн, yдек = yодн / wодн
• Перевод декартовых координат в однородные:
xодн = xдек, yодн = yдек, wодн=1
11.
Для нахождения коэффициентов прямой по координатам двух ее точек
нужно решить следующую систему уравнений.
Для определения координат точки пересечения прямых – следующую:
В пересечении двух параллельных прямых образуется точка
с координатами xодн=x0, yодн=y0, wодн=0, ее декартовы координаты
составляют xдек = xодн / 0 = ∞, yдек = yодн / 0 = ∞, такая точка бесконечно
удалена от начала координат.
12.
Аксонометрические проекции и тени от параллельных лучей.
13.
14.
15.
Сканирование и ксерокопирование документов и изображений.
16.
A’A
17.
y A’φ°
A
x
18.
-осевая симметрия относительно оси y: k = –1, m = 1; относительно оси x: k = 1, m= –1.
подобие/гомотетия (относительно начала координат): k=m.
Неравномерное растяжение/сжатие (относительно начала координат): k≠m.
y
y
A
A’
A
x
A’
x
19.
Последовательность (композиция) геометрических преобразований
также является геометрическим преобразованием.
В аналитической форме это выражается следующим образом:
Пусть M1, M2, …, Mn – матрицы преобразований, которые применяются
к точкам фигуры последовательно, тогда их последовательность
можно заменить одним преобразованием, матрица которого имеет вид:
M = M1×M2×…×Mn
Это позволяет при различных ограничениях инструментов выполнять
более сложные преобразования как композиции простых. Например,
Вращение вокруг произвольной точки =
Перенос начала координат в данную точку ×
Вращение вокруг начала координат ×
Перенос начала координат в прежнее положение
20.
Специальные режимы фотосъемки .
Преобразование картографических проекций.
21.
Вставка растрового изображения.
Построение предполагаемой горизонтали или вертикали.
Измерение угла и поворот растрового изображения.
Замер масштабной линейки (шкалы).
Масштабирование растрового изображения.
φ°
22.
В рамках лекции мы рассмотрели.1. Что такое и какие бывают геометрические
преобразования.
2. Математические модели геометрических
преобразований.
3.
Инструменты геометрических преобразований
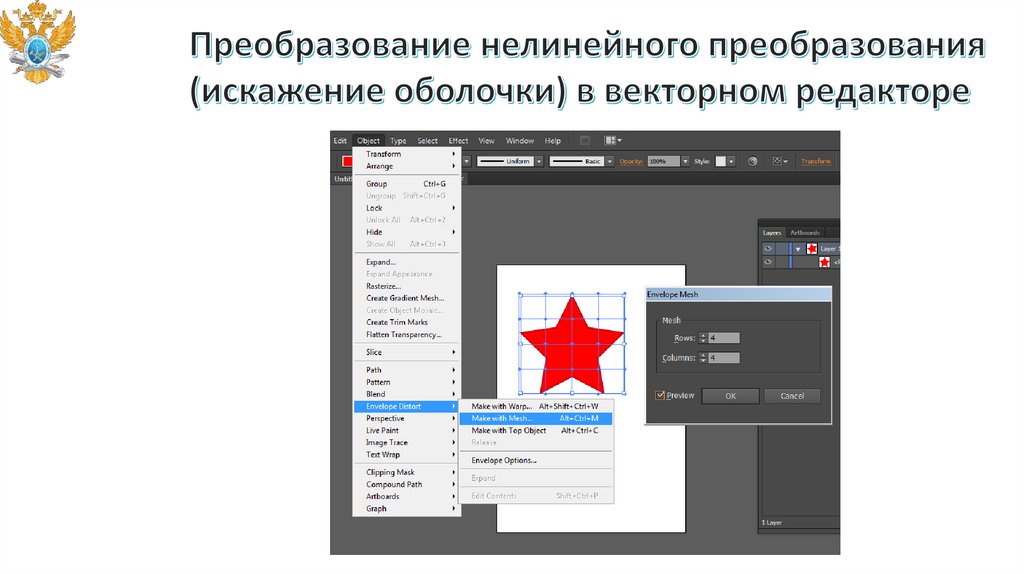
в векторном редакторе.
23.
24.
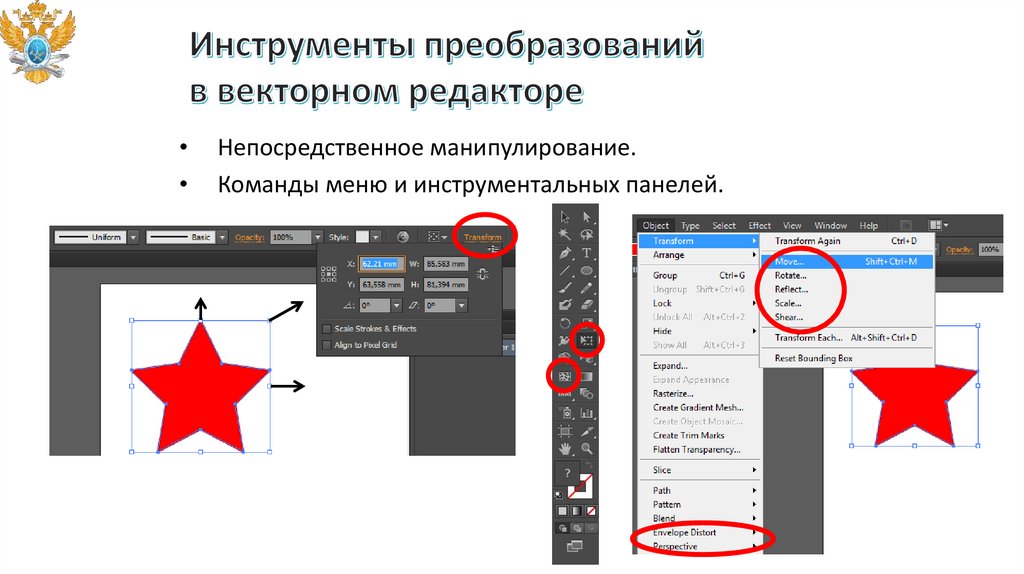
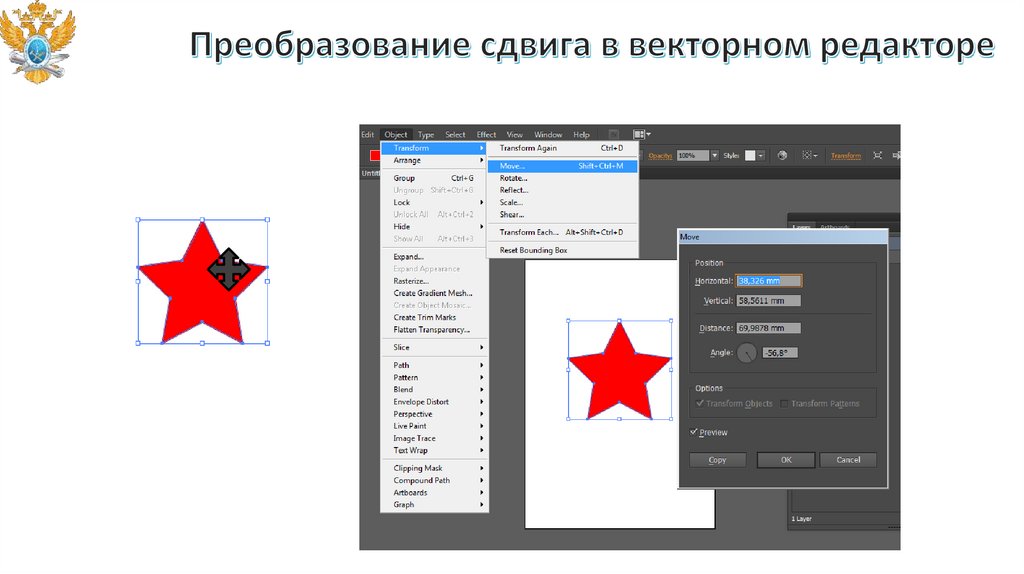
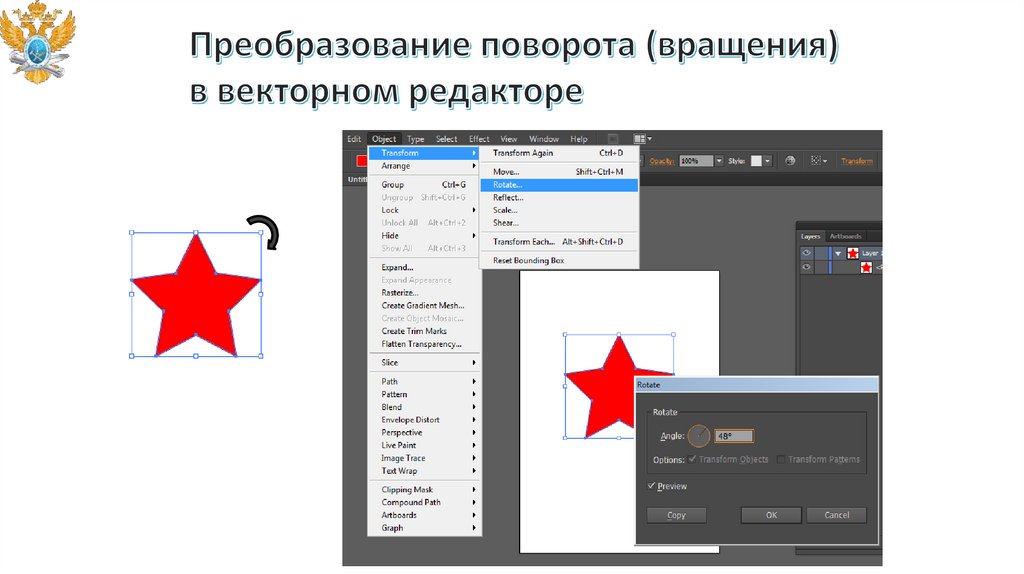
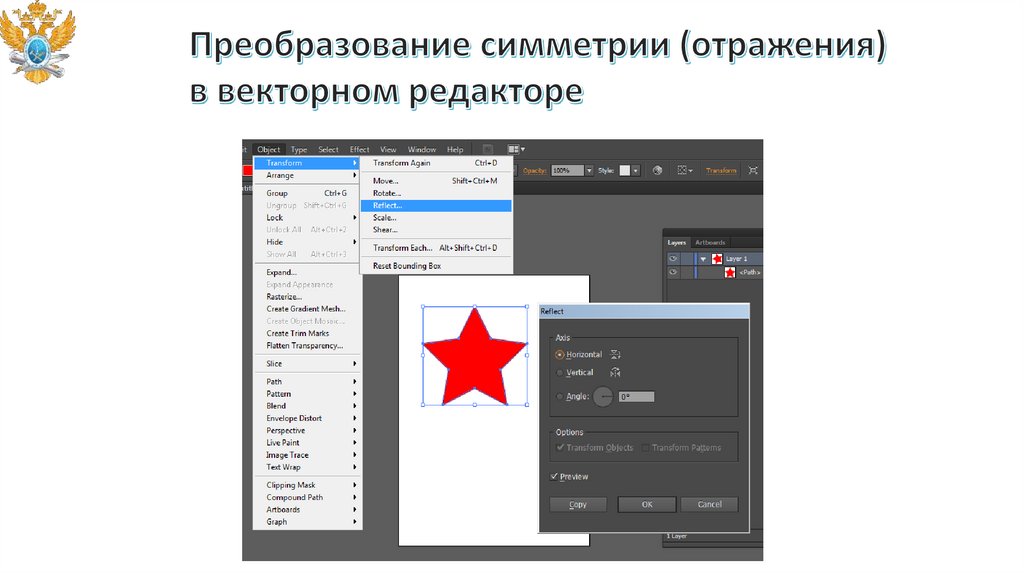
Непосредственное манипулирование.
Команды меню и инструментальных панелей.



















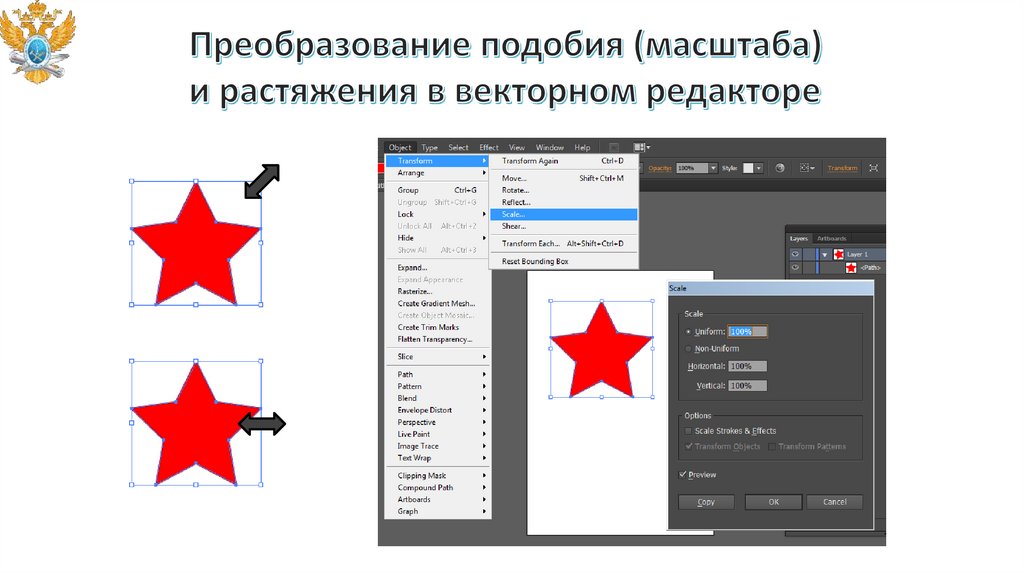
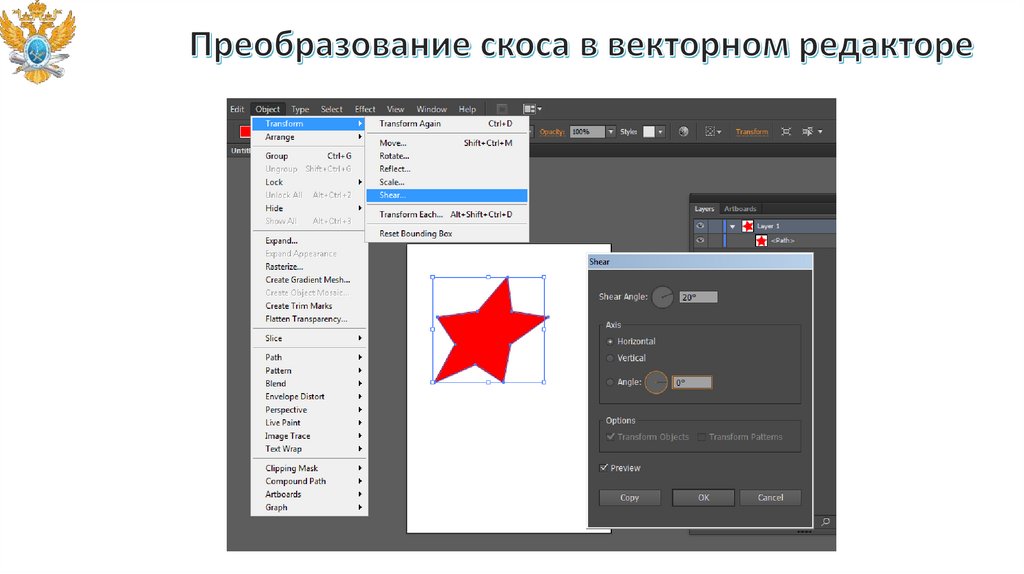
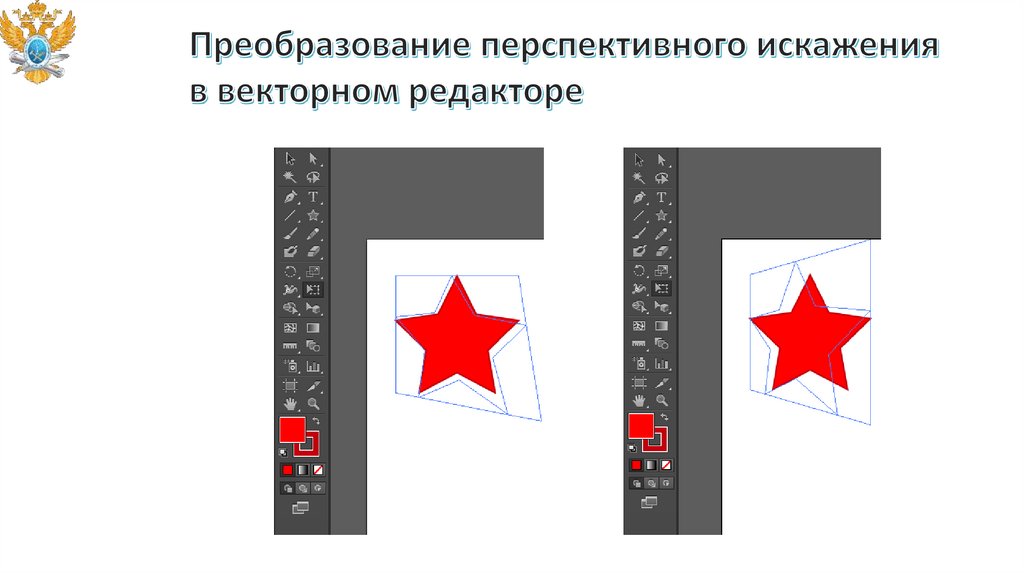
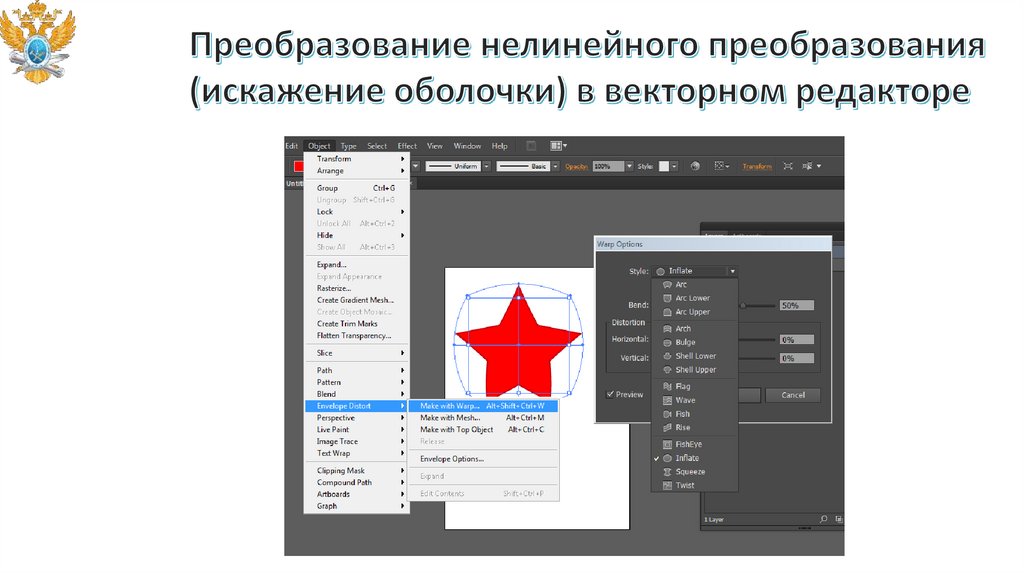
 software
software








