Начертательная геометрия. Инженерная и компьютерная графика

1.

2.

1.
2.
3.
4.
5.
Фигуры и объекты – основа векторной
графики.
Геометрические фигуры и их параметры.
Геометрические построения.
Некоторые задачи на построение.
Сплайны и их применение. Кривые Безье

3.

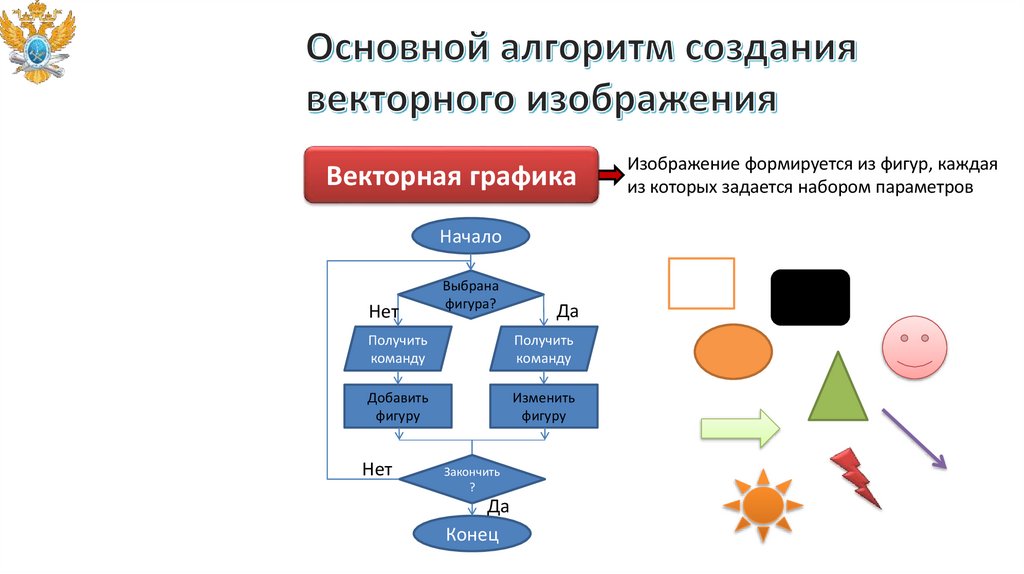
Векторная графика
Начало
Нет
Выбрана
фигура?
Да
Получить
команду
Получить
команду
Добавить
фигуру
Изменить
фигуру
Нет
Закончить
?
Да
Конец
Изображение формируется из фигур, каждая
из которых задается набором параметров

4.

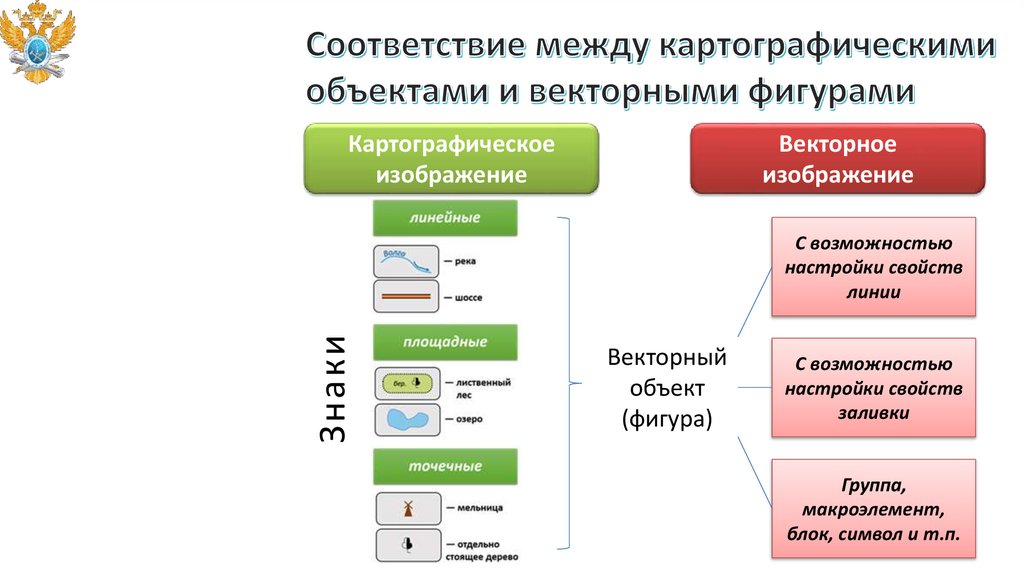
Картографическое
изображение
Векторное
изображение
Знаки
С возможностью
настройки свойств
линии
Векторный
объект
(фигура)
С возможностью
настройки свойств
заливки
Группа,
макроэлемент,
блок, символ и т.п.

5.

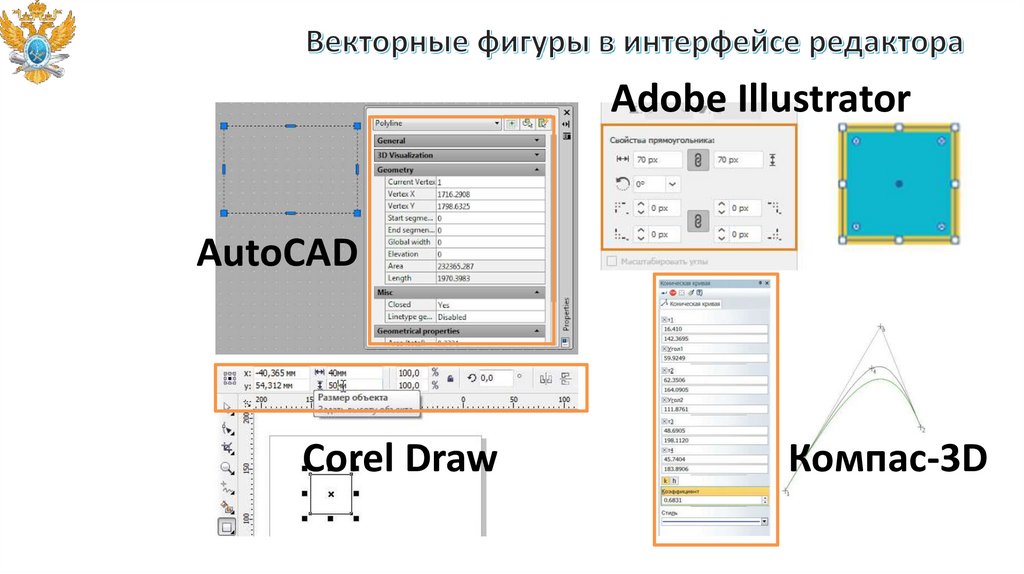
Adobe Illustrator
AutoCAD
Corel Draw
Компас-3D

6.

Фигура (в векторной графике) – информационный объект, имеющий
определенный тип и набор именованных характеристик (свойств),
которые полностью определяют внешний вид и поведение фигуры.
Свойства фигуры
Параметры
Надпись
Атрибуты
Параметры (геометрические свойства) – определяют размеры (форму) и
расположение фигуры.
Атрибуты (негеометрические свойства) – определяют подтип (число
вершин правильного многоугольника), отображение (цвет, стиль, узор,
градиент, тень, прозрачность, порядок прорисовки и др.), аннотации
(надпись, дополнительные знаки) и др.

7.

Фигура (в геометрии) – любое множество точек (точка, прямая, отрезок,
луч, окружность, дуга, треугольник, прямоугольник и др.)
Геометрические параметры
Форма
Положение
Общее число параметров фигуры: e = q + p, – величина постоянная!
q – параметры положения (внешние параметры), определяют
расположение фигуры относительно других фигур или начала координат.
p – параметры формы (внутренние параметры) – определяют размеры
(форму) фигуры, расположение частей фигуры относительно друг друга.

8.

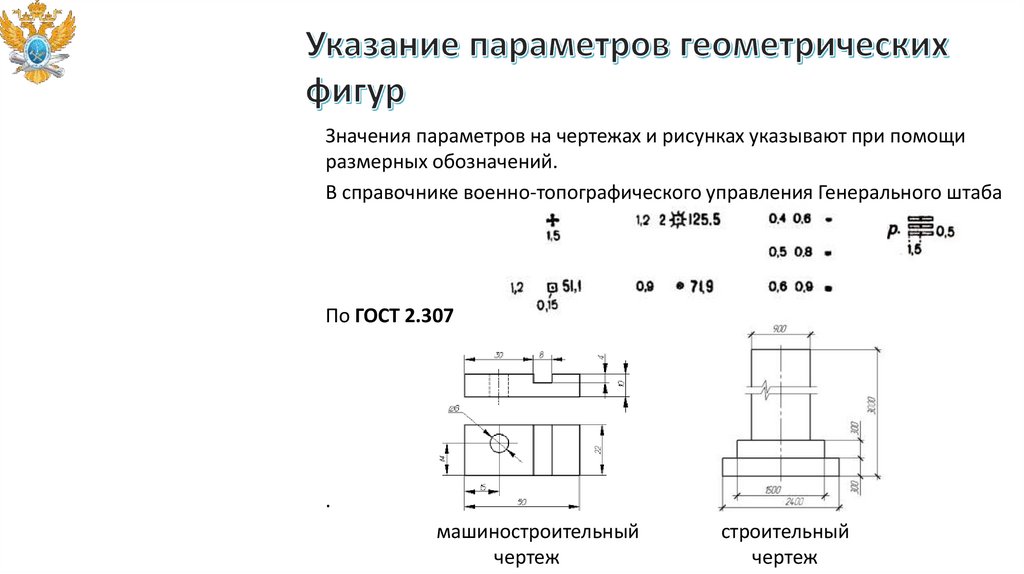
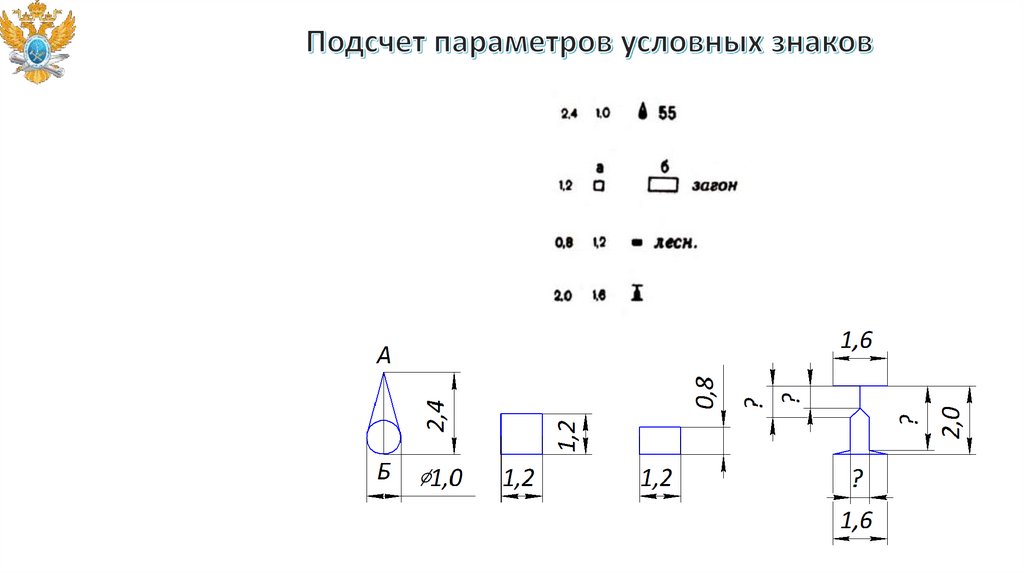
Значения параметров на чертежах и рисунках указывают при помощи
размерных обозначений.
В справочнике военно-топографического управления Генерального штаба
По ГОСТ 2.307
.
машиностроительный
чертеж
строительный
чертеж

9.

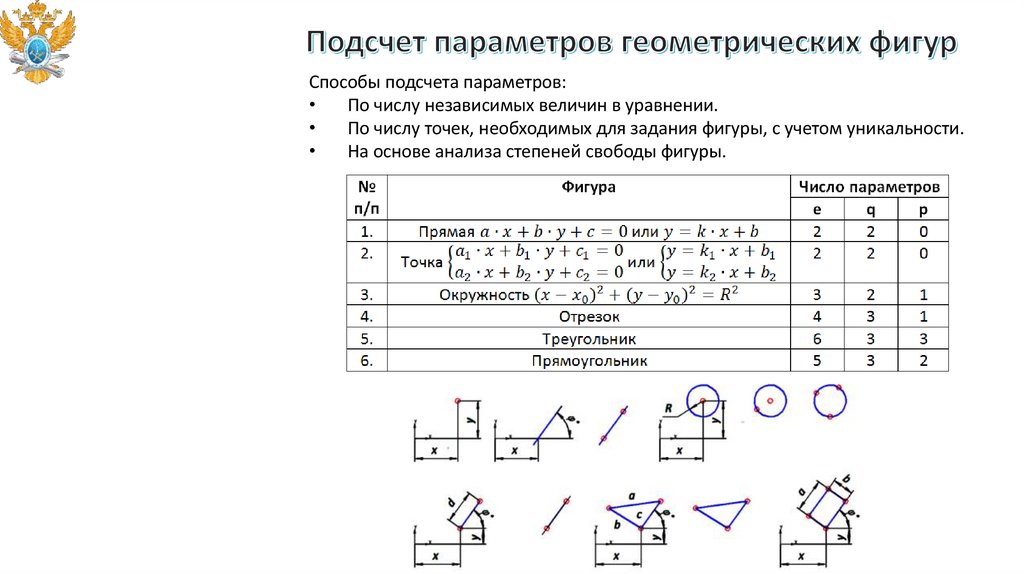
Способы подсчета параметров:
По числу независимых величин в уравнении.
По числу точек, необходимых для задания фигуры, с учетом уникальности.
На основе анализа степеней свободы фигуры.

10.

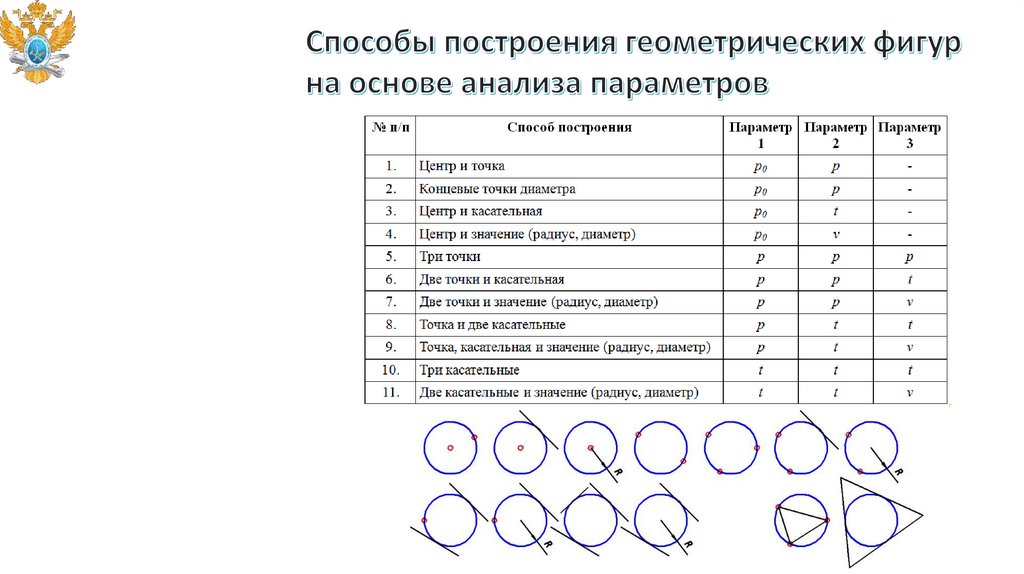
11.

12.

Геометрическая задача на построение (конструктивная задача
– КЗ) состоит в построении геометрической фигуры по
заданным условиям. КЗ может быть:
1) Определенной (конечное число решений).
2) Неопределенной (бесконечное число решение).
3) Переопределенной (в общем случае не имеет решений).
Определенность задачи выявляется на основе анализа числа
параметров фигуры и условий задачи.
Определенная КЗ имеет по крайней мере одно решение!
Можно его найти точно или только приближенно зависит
от используемых инструментов.

13.

Геометрический инструмент – это задача на построение
простейшей фигуры, решение которой считается известным.
Самые известные геометрические инструменты:
односторонняя и двухсторонняя линейки, циркуль, угольник.

14.

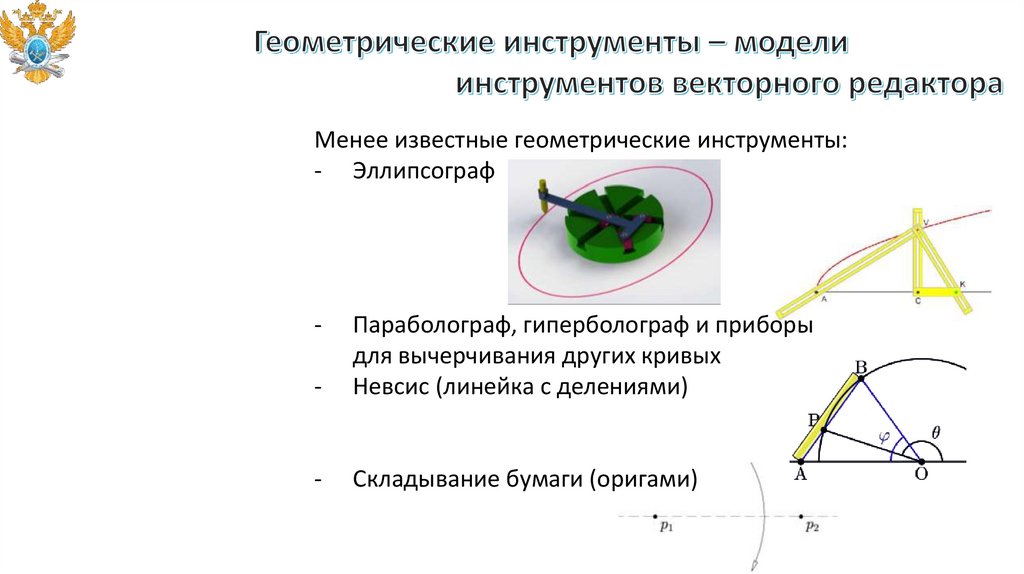
Менее известные геометрические инструменты:
- Эллипсограф
-
Параболограф, гиперболограф и приборы
для вычерчивания других кривых
Невсис (линейка с делениями)
-
Складывание бумаги (оригами)

15.

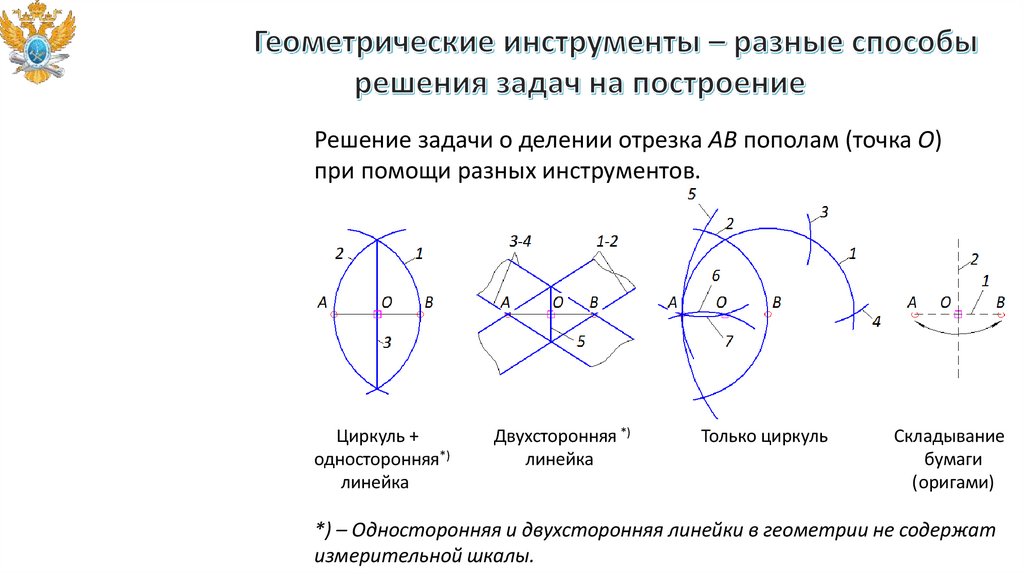
Решение задачи о делении отрезка AB пополам (точка O)
при помощи разных инструментов.
Циркуль +
односторонняя*)
линейка
Двухсторонняя *)
линейка
Только циркуль
Складывание
бумаги
(оригами)
*) – Односторонняя и двухсторонняя линейки в геометрии не содержат
измерительной шкалы.

16.

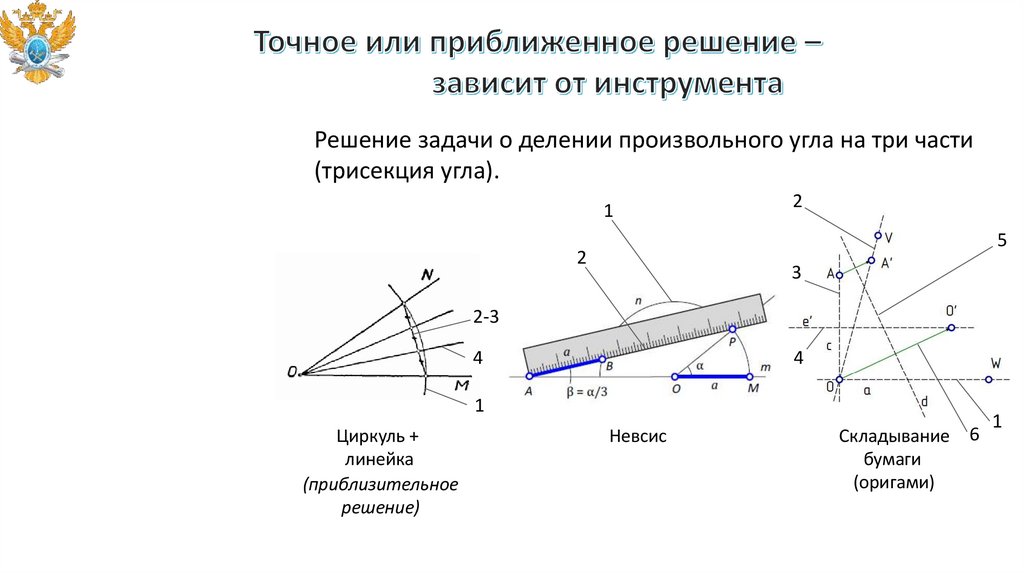
Решение задачи о делении произвольного угла на три части
(трисекция угла).
1
2
5
2
3
2-3
4
4
1
Циркуль +
линейка
(приблизительное
решение)
Невсис
Складывание
бумаги
(оригами)
6
1

17.

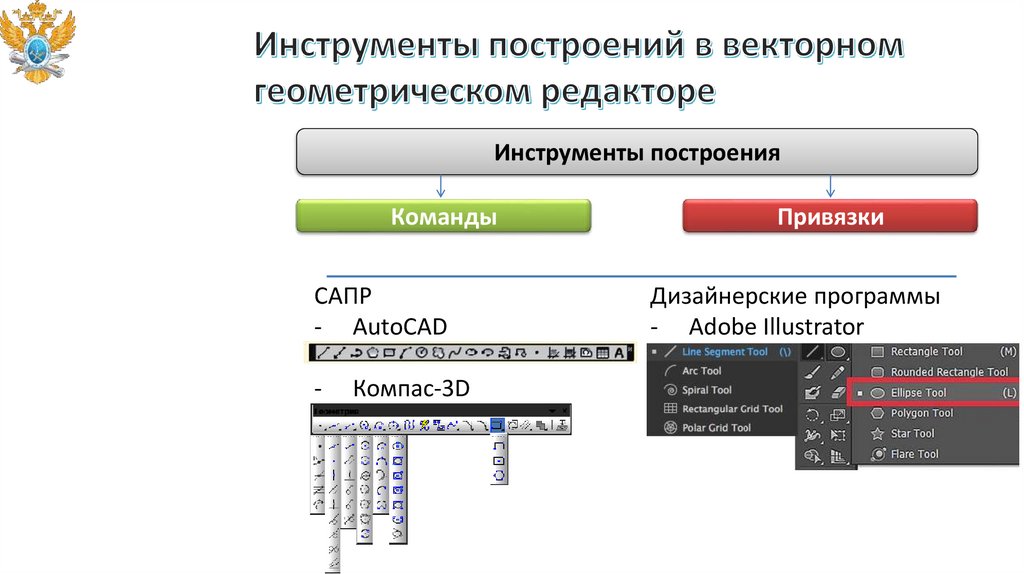
Инструменты построения
Команды
САПР
- AutoCAD
-
Компас-3D
Привязки
Дизайнерские программы
- Adobe Illustrator

18.

Построить прямую, перпендикулярную данной, через данную
точку. Параметрический анализ:

19.

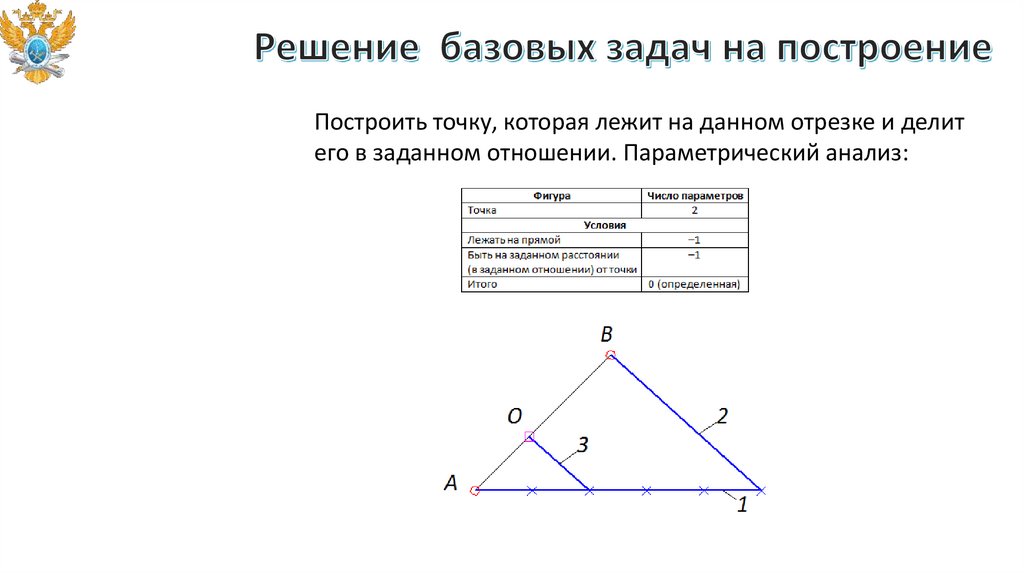
Построить точку, которая лежит на данном отрезке и делит
его в заданном отношении. Параметрический анализ:

20.

Построить прямую, параллельную данной, через данную
точку.
Построить прямую, перпендикулярную данной, через данную
точку.
90°

21.

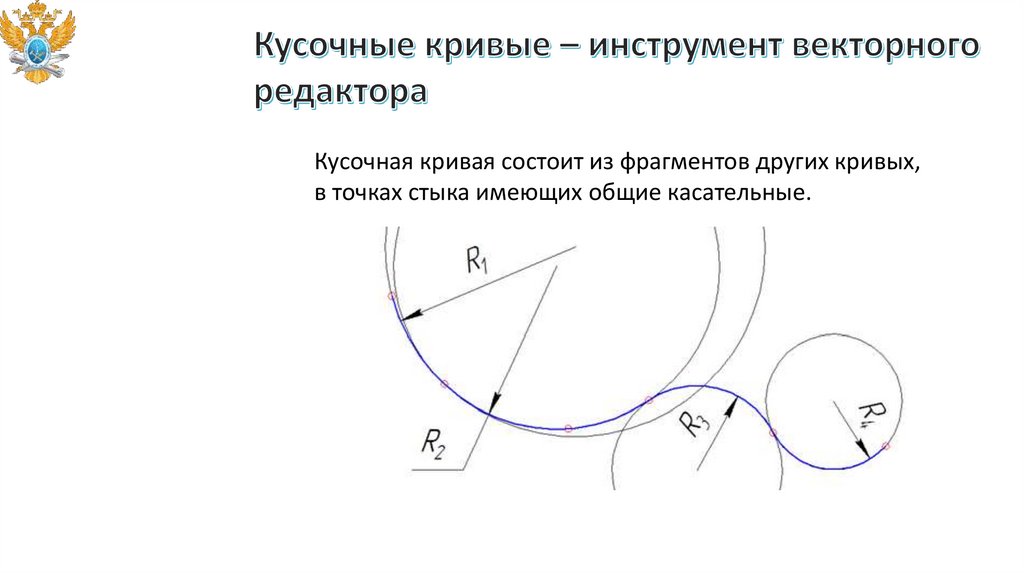
Кусочная кривая состоит из фрагментов других кривых,
в точках стыка имеющих общие касательные.

22.

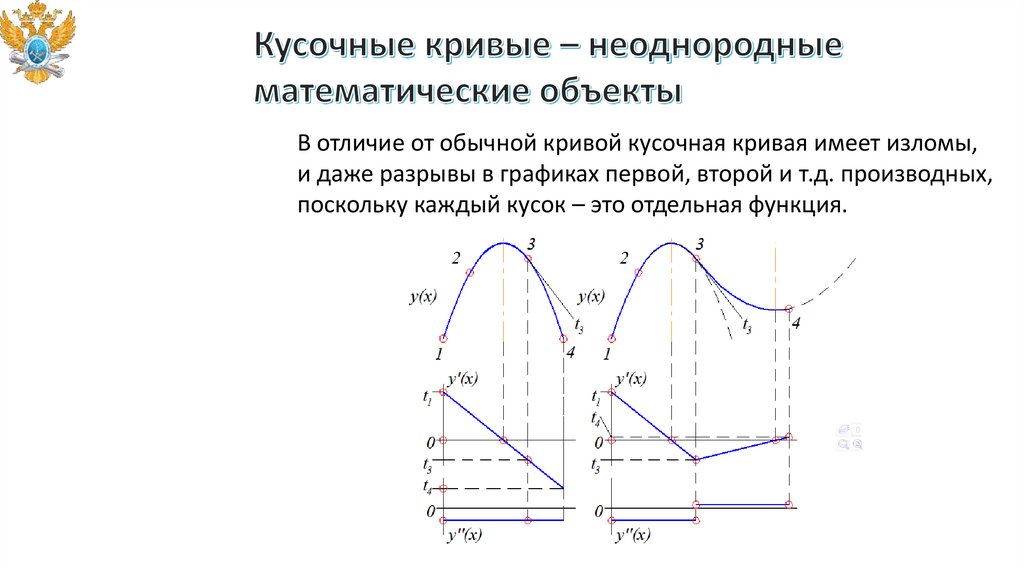
В отличие от обычной кривой кусочная кривая имеет изломы,
и даже разрывы в графиках первой, второй и т.д. производных,
поскольку каждый кусок – это отдельная функция.

23.

Сплайн (spline) – упругая рейка, по которой проектировщик
проводил плавную кривую через заданные точки.
Математической моделью рейки, зафиксированной
в отдельных точках, оказалась кусочная кривая, составленная
из дуг кубических кривых.

24.

Разновидности сплайнов:
• Кубические сплайны.
• Кривые Эрмита и Катмалла-Рома.
• Сплайны Бесселя и Акимы.
• Монотонные сплайны.
• Напряженные сплайны.
• Тригонометрические сплайны.
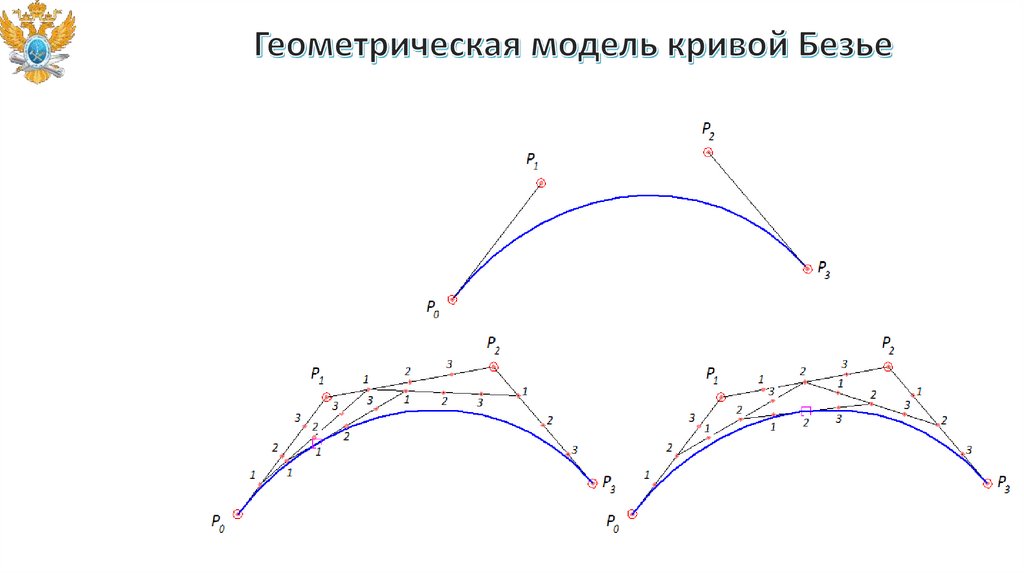
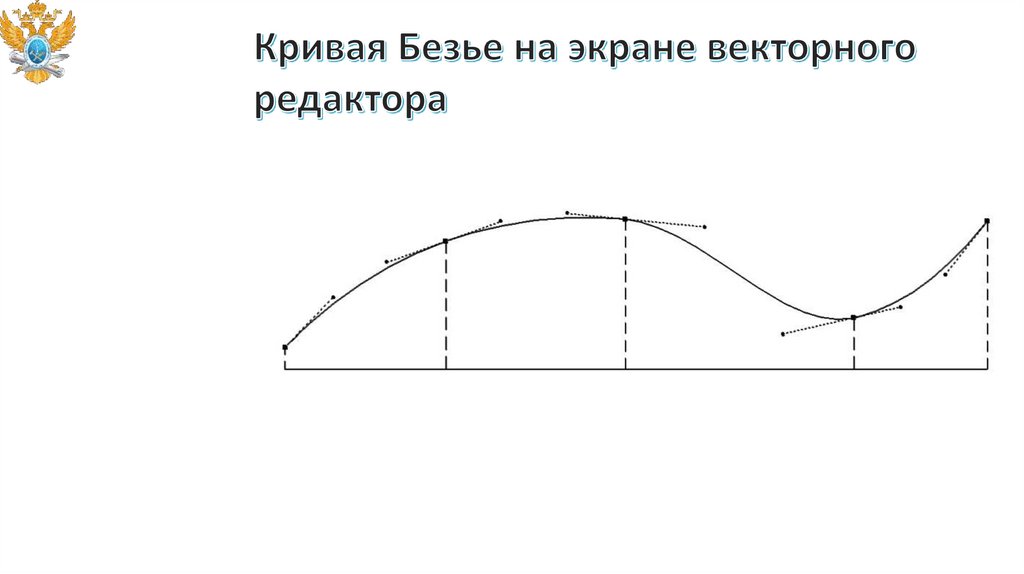
• Кривые Безье.
• B-сплайны и NURBS.
• Интегродифференциальные сплайны и др.

25.

26.

27.

28.

В рамках лекции мы рассмотрели.
1. В чем состоит процесс создания векторного
изображения.
2. Математические модели векторных фигур
(геометрические фигуры и параметры) и
команд векторного редактора (построения).
3.
Некоторые базовые построения и их реализацию
в геометрии и векторном редакторе.
4.
Что такое сплайны и, в частности,
кривые Безье.

29.

30.

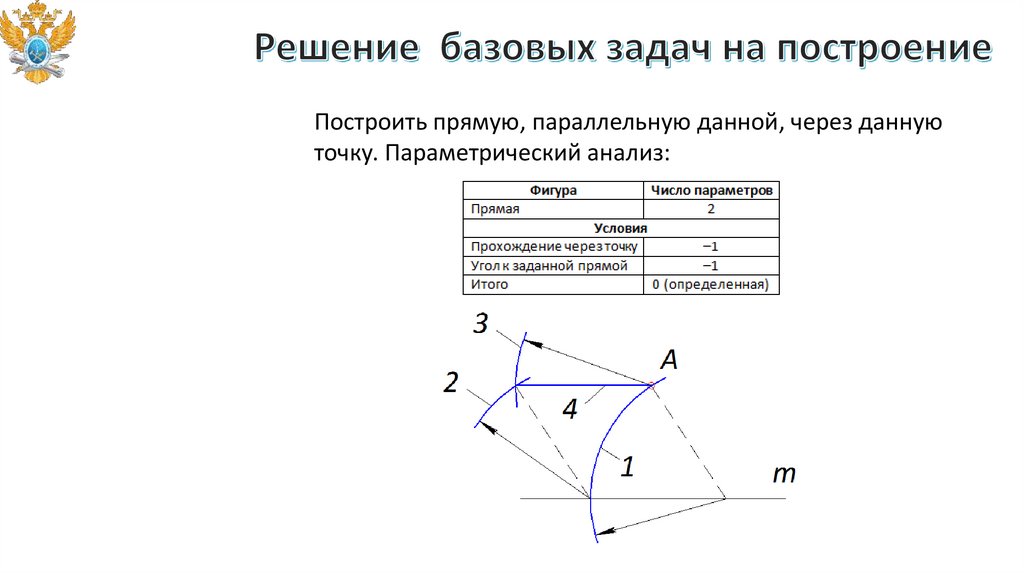
Построить прямую, параллельную данной, через данную
точку. Параметрический анализ:

31.

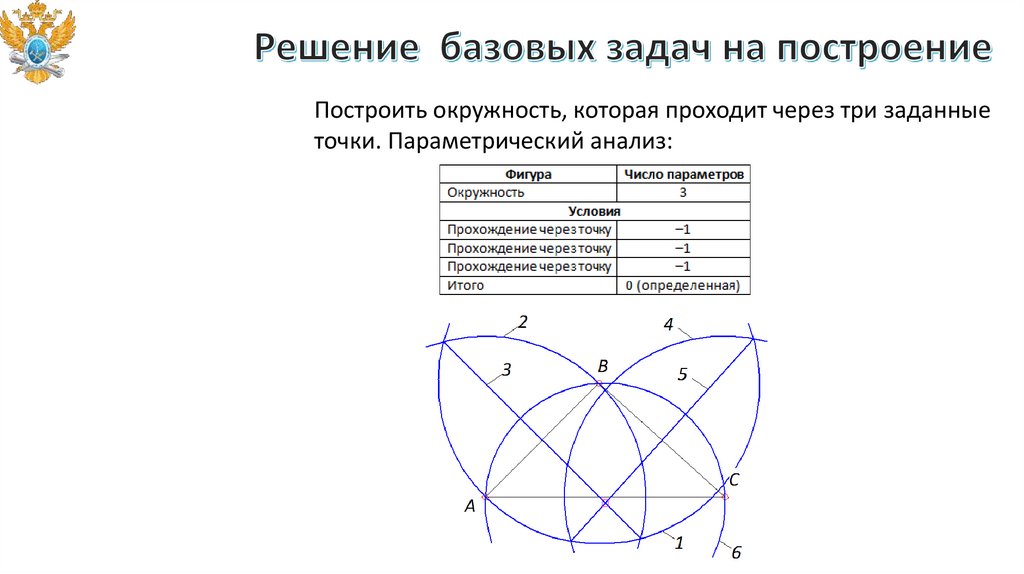
Построить окружность, которая проходит через три заданные
точки. Параметрический анализ:

32.

Построить окружность с заданным центром, проходящую
через данную точку.
14
3
7-8
1
4
12
6
5
11
2
10
13
9