Similar presentations:
Анализ и особенности матрицы
1.
Лекция 2.Анализ и особенности матрицы
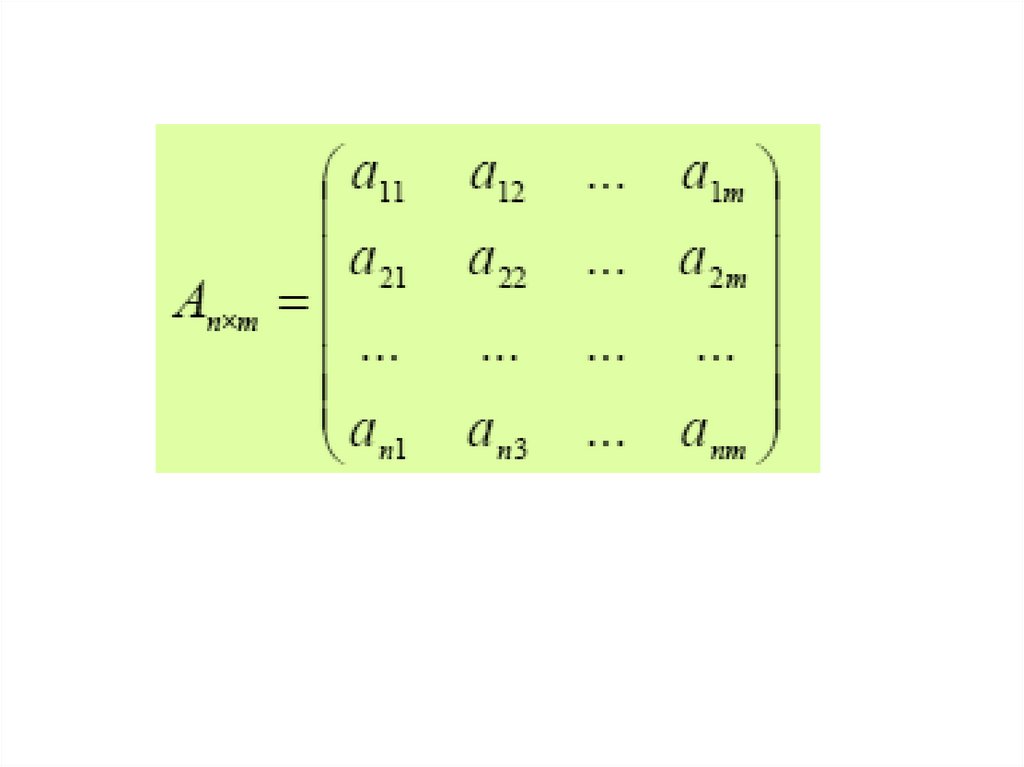
1. Матрица и ее виды
2. Основные операции над матрицами
3. Определитель матрицы
2.
Рассмотрим прямоугольную матрицу. Если вэтой матрице выделить произвольно k строк и
k столбцов, то элементы, стоящие на
пересечении выделенных строк и столбцов,
образуют квадратную матрицу k-го порядка.
Определитель этой матрицы называется
минором k-го порядка матрицы А.
3.
Наибольший из порядков миноров даннойматрицы, отличных от нуля, называется рангом
матрицы. Если ранг матрицы А равен r, то это
означает, что в матрице А имеется отличный от
нуля минор порядка r, но всякий минор
порядка, большего чем r, равен нулю. Ранг
матрицы А обозначается через r(A).
4.
Элементарными называются следующиепреобразования матрицы:
1) перестановка двух любых строк (или столбцов)
2) умножение строки (или столбца) на отличное от
нуля число,
3) прибавление к одной строке (или столбцу)
другой строки (или столбца), умноженной на
некоторое число.
5.
Две матрицы называются эквивалентными,если одна из
них получается из
другой с
помощью конечного множества элементарных
преобразований.
Эквивалентные матрицы не являются, вообще
говоря, равными, но их ранги равны. Если матрицы
А и В эквивалентны, то это записывается так:
A
B
6.
Диагональная матрица, у которой все элементыглавной диагонали равны 1, называется единичной
и обозначается En
7.
8.
Если число столбцов матрицы равно числу строк(n=m), то матрица называется квадратной.
9.
Квадратная матрица виданазывается диагональной матрицей.
10.
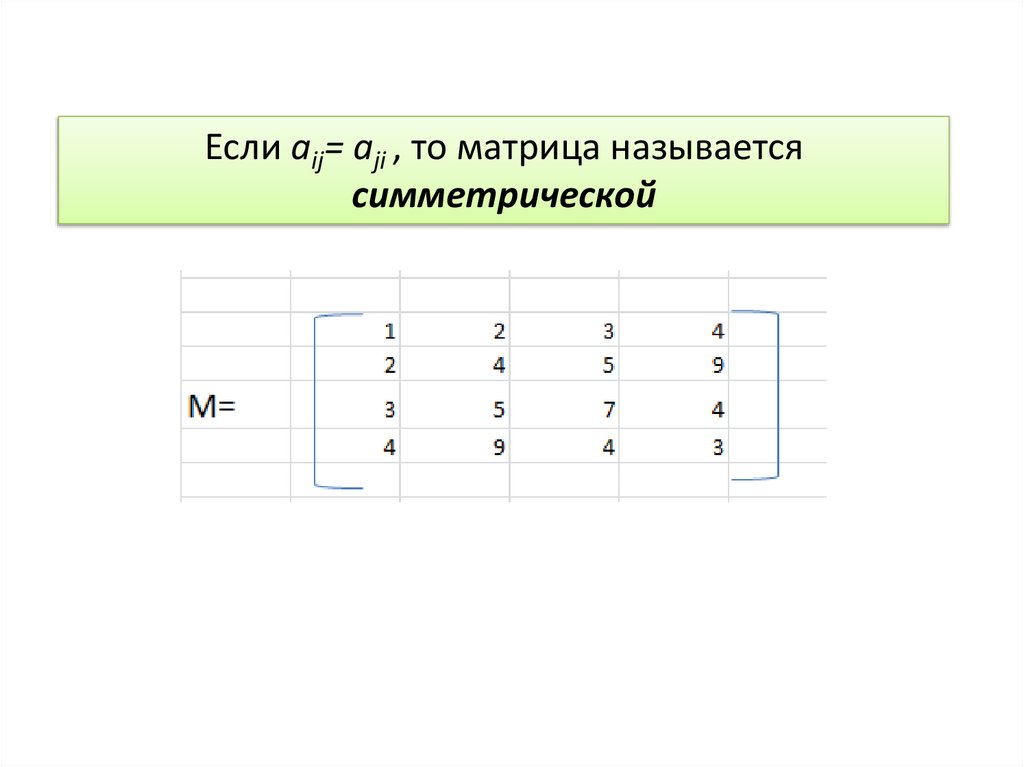
Если aij= aji , то матрица называетсясимметрической
11.
Матрицы A и B одного размера называютсяравными, если равны их соответствующие элементы
12.
Основные операции над матрицами1. Сложение и вычитание матриц
2. Умножение матрицы на число
3. Произведение матриц
4. Транспонирование матриц
5. Нахождение обратной матрицы
13.
Сложение и вычитание матриц сводится ксоответствующим операциям над их
элементами. Самым главным свойством этих
операций является то, что они определены
только для матриц одинакового размера.
14.
Суммой (разностью) матриц A и B одного и того жеразмера mn× является матрица, того же размера ,
элементами которой являются соответственно сумма
cij = aij ± bij . (разность) элементов исходных матриц A и B:
Записывают С = А ± В.
15.
Основные свойства:1. А + В= В+A
2. (A+B)+C=A+(B+C)
3. если С = А + В, то B=C-A и A=C-B
4. A+Ο=A, A-A=Ο, где – нулевая матрица
16.
Произведением матрицы А любого размера напроизвольное число α называется матрица С того же
размера, что и матрица А, элементы которой равны
соответствующим элементам матрицы А,
умноженным на это число α:
17.
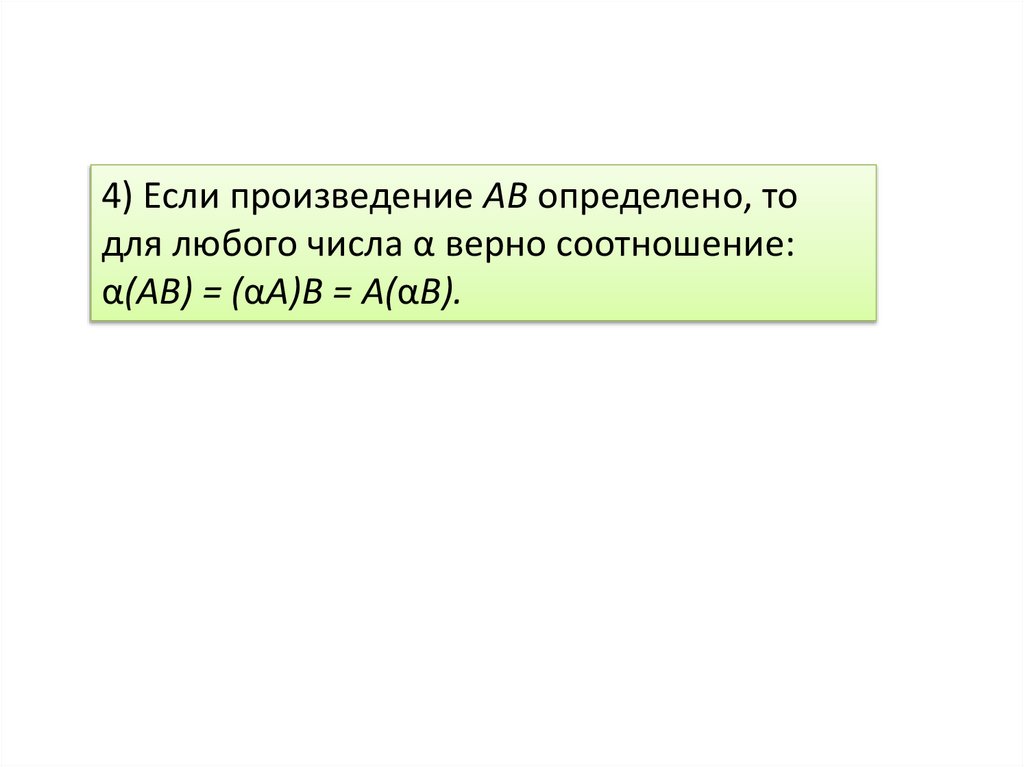
Основные свойства1.























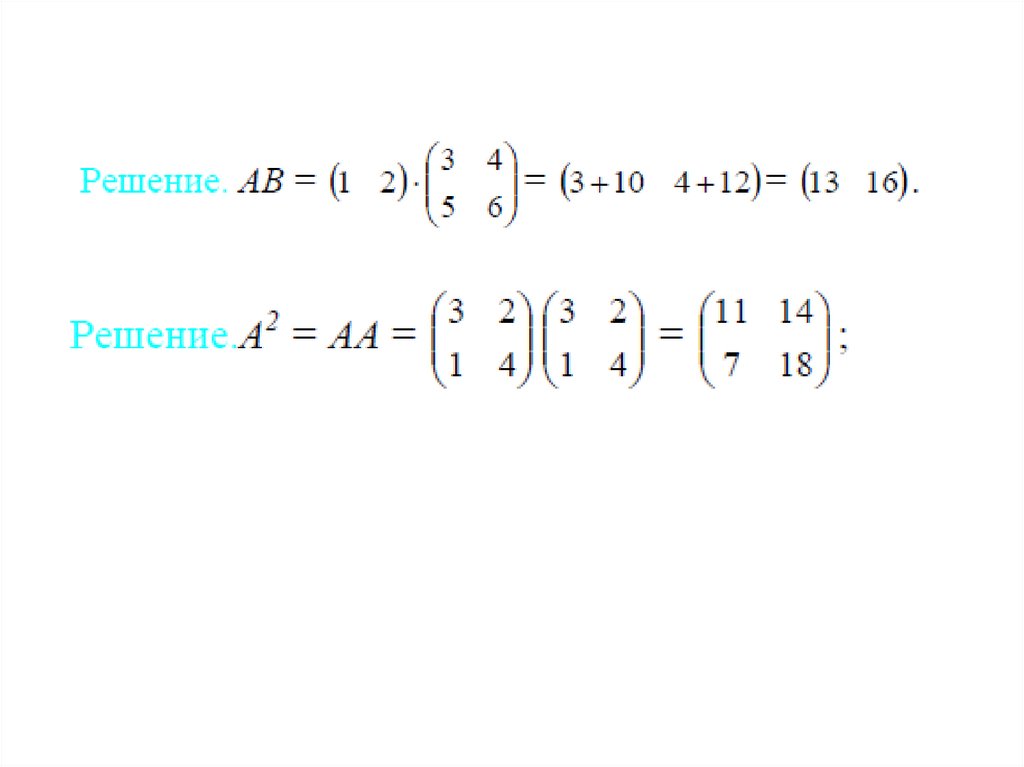












 mathematics
mathematics








